引用本文
王寅同, 王建东, 陈海燕. 时间序列降维及机场噪声中的机型识别.吉林大学学报:工学版, 2016, 46(4): 1202-1208
WANG Yin-tong, WANG Jian-dong, CHEN Hai-yan. Time series dimensionality reduction and aircraft model recognition in airport-noise. Journal of Jilin University Engineering and Technology Edition, 2016, 46(4): 1202-1208  
Permissions
Copyright©2016, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
时间序列降维及机场噪声中的机型识别
王寅同, 王建东, 陈海燕
南京航空航天大学 计算机科学与技术学院,南京 210016
通讯作者：王建东 (1945-), 男, 教授,博士生导师.研究方向:人工智能, 数据挖据,网络安全.E-mail:aics@nuaa.edu.cn

作者简介:王寅同 (1987-), 男, 博士研究生.研究方向:数据挖掘, 数据降维.E-mail:wangyintong@nuaa.edu.cn

基金:国家自然科学基金重点项目(61139002); 中央高校科研业务费专项资金项目(NS2015091); 江苏省博士后科研资助计划项目(1301013A)
摘要

为了提高非完整标记的高维机场噪声数据的处理速度和效率,研究了时间序列降维及机场噪声中的机型识别问题。首先采用概率类和不相关判别的半监督局部Fisher方法(SLFisher)得到降维转换矩阵,再将时间序列数据由高维空间映射到低维空间,最后在低维数据上进行k最近邻分类(kNN)。在国内某机场的实测噪声数据上的实验结果表明,SLFisher降维后机场噪声事件数据的机型识别效果取得显著提升。

关键词: 人工智能; 机场噪声; 时间序列; 降维; 机型识别
中图分类号:TP18 文献标志码:A 文章编号:1671-5497(2016)04-1202-07
Time series dimensionality reduction and aircraft model recognition in airport-noise
WANG Yin-tong, WANG Jian-dong, CHEN Hai-yan
College of Computer Science and Technology,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China
Abstract

In order to enhance the efficiency and effectiveness of the processing of high dimensional airport-noise data with incomplete labels, the time series dimensionality reduction and aircraft model recognition in airport-noise are investigated. First, we use semi-supervised local fisher method, which is based on probability class and uncorrelated discriminant (SLFisher), to obtain the transformation matrix of dimensionality reduction. Next, the high dimensional time series data are mapped to the low-dimensional space. Finally, we apply the k Nearest Neighbor (kNN) classifier to classify the obtained low-dimensional data. Experimental results on measured airport-noise data demonstrate that the performance of aircraft model recognition is remarkably improved after the dimensionality reduction achieved using SLFisher.

Keyword: artificial intelligence; airport-noise; time series; dimensionality reduction; aircraft models recognition
0 引 言

随着社会的进步和我国民航事业的不断发展, 国内主要机场的航班安排正在变得紧凑, 随之而来的机场噪声也日渐严重。为了更好地利用机场噪声时间序列数据, 分析不同机型对环境噪声影响的大小, 需要对每天的机场噪声事件数据值进行研究。从时域上来看, 机场噪声事件数据值构成一种时间序列, 可将时间序列分析算法运用到机型识别研究中。由于时间序列具有数据数量大、维度高、噪声干扰和短期波动等特点, 直接在原始时间序列上直接采用欧式距离或动态时间规整度量来进行时间序列的聚类或分类, 其处理效果并不佳[1, 2, 3, 4, 5, 6]。因此, 在时间序列数据上引入降维算法, 能够将其由高维空间映射到对应的内在本质的低维空间, 从而降低处理时间序列数据所需的时间复杂度和空间复杂度[7, 8]。更重要的是, 在降维后的时间序列数据上运用现有的聚类或分类算法能够有效地降低计算复杂度, 并获得更好的处理效果。

一般而言, 降维是将高维空间中观测得到的数据通过线性或非线性映射方式投影到低维空间中, 这样就能够发现隐藏在高维观测数据中有意义的、可以揭示数据内在本质的低维结构。降维可以改善高维数据的维数灾难问题, 提高其分类准确性、可视化以及最终结果的可解释性。近年来关于时间序列的降维方面已开展了很多研究工作, 如Xing等[9]提出了一种使用成对约束学习马氏距离度量的凸优化算法; 邹朋成等[10]提出了一种利用动态时间弯曲距离在捕捉时序特性上的优势, 自动生成成对约束信息的时间序列度量算法。时间序列度量算法利用了时间序列事件标记的部分或全部信息, 以提高时间序列聚类、分类的性能, 但他们仍然是在高维数据上进行时间序列数据处理和新增数据的重新计算, 导致时间序列度量算法的时间复杂度和空间复杂度仍然居高不下。另外, 主成分分析(Principle component analysis, PCA)[11, 12]作为一种经典的对高维数据进行降维的算法, 将高维数据通过线性变换的方式投影到低维空间中, 得到数目较少的、彼此不相关的属性子集; 符号化表示[13, 14, 15]能够通过等宽离散化算法将时间序列的实数值映射到有限的符号集; Park等[16]提出的极值点拟合及其延续算法, 利用时间序列数据的单调变化属性, 抽取其中的极值点作为特征数据, 实现对时间序列的压缩并保留其主要变化特征的目的。上述时间序列数据降维工作的共性是仅针对时间序列数据本身, 而较少考虑时间序列事件及标记。

针对上述问题, 本文研究了时间序列降维及机场噪声中机型识别问题。首先采用概率类和不相关判别的半监督局部Fisher方法(SLFisher)得到降维转换矩阵, 再将时间序列数据由高维空间映射到对应的低维空间, 最后在低维数据上进行k最近邻分类。实验对比了传统的主成分分析(PCA)[11]和线性判别分析(LDA)[18]降维算法, 并验证了SLFisher算法的有效性和优越性。

1 相关工作

时间序列数据间的相似度量是时间序列数据挖据的重点研究内容之一, 其中动态时间规整(Dynamic time warping, DTW)作为一种常用序列数据度量算法, 由Shakoes和Chiba[19]于1978年提出, 其主要特点是综合考虑时间序列事件中时间序列间相位移动、各阶段事件持续长度差异等情形, 因而DTW的时间序列度量结果比较符合人们的直觉观察。另外, DTW度量距离适用于一阶最近邻分类, 且在大量实测时间序列数据集上取得较好的分类效果[20, 21]。另外, 作为一种不满足三角不等式的距离度量方式, 使得DTW得到的相似性不具备传递性, 极大地影响了在聚类分类中的应用[22]。对此, 研究人员对DTW进行了延展, 如Shimodaira等[23]和Cuturi等[24, 25]利用DTW构造适用于时间序列的和度量, 在一定程度上改善DTW的不足, 并应用到面部表情识别和人体运动行为分析等复杂时间序列聚类问题中。

本文采用DTW度量机场噪声事件的时间序列数据的相似性, 并进一步根据国内某机场的实测噪声数据确定不同飞机机型的标记。

2 基于SLFisher的时间序列降维
2.1 时间序列降维问题的定义

机场噪声监测装置不间断地记录所在地理位置的噪声分贝值, 但飞机掠过其上空却是一个短暂的过程。如果直接使用原始监测数据, 则意味着在大量无用的环境背景噪声上进行分析, 无法客观有效地从机场噪声时间序列数据中分析所需结果。同时, 数据维度随着监测装置的持续采集也在不断地增大, 使得机场噪声时间序列数据在后续处理的计算复杂度和空间复杂度骤增。

针对上述问题并结合机型识别的目的, 定义单次起落(起飞或降落)作为一个机场噪声事件, 事件持续时间所产生的连续噪声分贝值组成机场噪声事件的时间序列数据, 并且将其标记为对应机型(或缺失)。由多次起飞(或降落)的机场噪声事件组成时间序列数据集, 其形式化表示为 X={x1, …, xn, xn+1, …, xn+m}, 第i机场噪声事件的时间序列数据 xi∈Rd(i=1, 2, …, n+m), 其中, d表示时间序列数据的维度, 其值由事件持续时间及噪声采集频率共同决定。时间序列数据集 X的前n个数据的机型标记 li∈{1, 2, …, c}, 后m个数据的机型标记缺失。

2.2 基于SLFisher的时间序列降维模型

SLFisher算法[17]是在经典维数约简Fisher判别分析基础上提出的。通过重构概率类使得无标记数据获得一个所属标记的概率, 数据对权值实现多模态分布数据距离的差异化, 以及不相关判别向量优化Fisher准则函数, 最终实现半监督。降维后的类间数据尽可能分离, 类内邻近数据尽可能紧凑且类内非邻近数据尽可能地保持。

SLFisher的目标函数:

(S(slb)-S(slw))T=λS(t)T1

从而SLFisher的转换矩阵 T是由等式(1)的 d个最大特征值 λ1≥λ2≥…≥λd所对应的特征向量 t1, t2, …, td组成。

SLFisher的半监督局部类间散度矩阵 S(slb)和半监督局部类内散度矩阵 S(slw)的定义如下:

Sslb=12∑i, j=1n+mWi, j(slb)xi-xjxi-xjT2Sslw=12∑i, j=1n+mWi, j(slw)(xi-xj)(xi-xj)T3

式中: Wi, j(slb)和 Wi, j(slw)分别表示类间数据对权值和类内数据对权值, 定义如下:

Wi, j(slb)=A~i, j(1/(n+m)-1/nli), 1(n+m), ififli=ljli≠lj4Wi, j(slw)=A~i, j/nli, 0, ififli=ljli≠lj5

式中: A~i, j表示类内数据对的启发式局部度量, 当数据 xi和 xj之间的距离较远而成为类内非邻近数据对时, 其相似度接近于0; 当两个数据距离不断缩小而成为类内邻近数据对时, 其相似度更加接近于1, 当且仅当两个数据完全一样时, 它们的相似度等于1。本文采用的启发式局部度量方式计算相似度矩阵 A~, 其中第i行第j列的数据定义如下:

A~i, j=pi, j·exp-‖xi-xj‖2σiσj6

式中: σi=‖xi-xi(k)‖表示数据 xi的局部度量, xi(k)是数据 xi的第k个非自身的最近邻数据, k是一个超参数, 取值为1, 数据xi和 xj属于标记 l的概率值 pi, j=pi(l)·pj(l), pi(l)表示 i数据属于 l标记的概率值, pj(l)表示 j数据属于 l标记的概率值[17]。

由等式(4)和(5)可知, 当属于同一类别的数据对接近时, 则半监督局部类间散度 Sslb取值大而半监督局部类内散度 Sslw取值小。当属于不同类别的数据对应该尽可能分离时, 则半监督局部类间散度 Sslb取值大, 并且半监督局部类内散度 Sslw取值为零。即这样可以使得SLFisher从高维数据映射到低维时, 半监督局部类间数据对尽可能地分离, 同时半监督局部类内邻近数据对尽可能地紧凑。其形式化表达式如下:

max∑i, j=1n+mWi, j(slb)(yi-yj)(yi-yj)T=max∑i, j=1n+mWi, j(slb)(TTxi-TTxj)(TTxi-TTxj)T=maxTTS(slb)T7min∑i, j=1n+mWi, j(slw)(yi-yj)(yi-yj)T=min∑i, j=1n+mWi, j(slw)(TTxi-TTxj)(TTxi-TTxj)T=minTTSslwT8

式中: yi和 yj是高维数据 xi和 xj分别在低维空间的表示形式, T是高维到低维的转换矩阵。式(7)表示不同类别的高维数据映射到低维空间上的相似度量值尽可能地小; 式(8)表示同类的高维数据映射到低维空间上的相似度量值尽可能地大。

2.3 基于SLFisher的时间序列降维实现

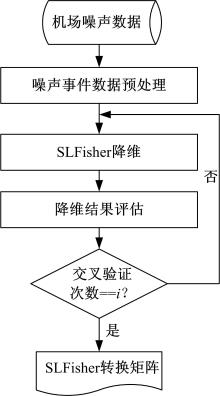
在机场噪声事件的时间序列数据上的SLFisher降维, 主要包括预处理、SLFisher降维和评估三个过程。首先, 在机场噪声监测点的连续噪声时间序列数据上, 波形的骤升/骤降为一个机场噪声事件, 截取固定时间长度的波形为一个机场噪声事件的时间序列, 并对照机场飞机起落(起飞或降落)事件日志, 增加时间序列的飞机机型标记(或缺失)。其次, 在机型标记不完整的高维时间序列数据上, 采用 i交叉验证的算法, 每份时间序列数据单独完成SLFisher降维, 得到时间序列的高维到低维的转换矩阵。然后, 通过转换矩阵对剩余的高维时间序列数据由转换矩阵映射到低维空间上, 由选定的分类算法评估转换矩阵的可信度。最后, 可信度最高的转换矩阵作为后续时间序列数据的降维矩阵, 其大小是高维维度乘以低维维度。

机场噪声事件的时间序列数据降维流程图和算法实现, 分别如图1和算法1所示。

图1 机场噪声时序数据降维流程图Fig.1 Flaw chart of the airport-noise time series data

算法1 机场噪声事件时间序列数据降维算法实现

输入:

(1)机场噪声多监测点数据data={d1, d2, …, dn}

(2)日志数据log={log1, log2, …, logn}

输出:

(1)机场噪声事件的时间序列数据降维转换矩阵T

(2)转换矩阵可信度C

算法:

(1)(X, L)=Preprocessing(data, log);

(2)tBest=null; cBest=0;

(3)for i-cross-validation

(4)T=SLFisher(X’ , L’ );

(5)c=Evaluating({X-X’ }, T, {L-L’ });

(6)If cBest < c then

(7)tBest=T; cBest=c;

(8)End if

(9)End for

(10)T=tBest; C=cBest;

3 实验及结果分析
3.1 实验数据集

实验数据为国内某枢纽机场噪声监测系统从2010年2月至8月的机场噪声监测数据, 并从分布在机场周围的21个监测点中选择4个代表位置的监测点, 其编号分别为NMT7、NMT10、NMT13和NMT19(机场前、后、左、右4个方位)。4个监测点获得的飞机起飞(或降落)的噪声事件数据, 分4组进行实验, 验证SLFisher的机场噪声数据降维对机型的识别能力, 数据集的具体内容如表1所示。由于监测点位置、气候和飞机发动机推力比等不同, 并非每个监测点都能采集到所有机场噪声事件数据, 这也是表1中各监测点数据集大小不一致的原因。噪声监测器的采集频率是每秒钟10个噪声值(单位dB), 从飞机降落(进入、减速、滑行、停稳)或是起飞(准备、加速、爬升、飞离)的角度讲, 单个噪声事件持续时间设定为3 min, 其噪声事件的时间序列总长度为1800。

表1 4个监测点的机场噪声时序数据 Table 1 Airport-noise time series data in the four monitors

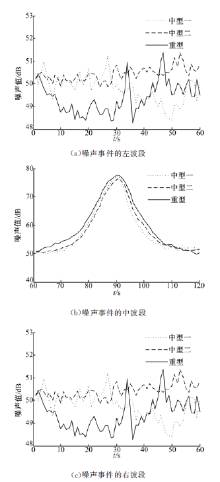
另外, 为了更好地完成机场噪声事件的机型识别, 根据飞机的最大起飞质量定义了三种机型。由于民航机场以中大型客机的起飞或降落为主, 质量小于7t的轻型飞机较少, 在此将7 t到136 t的中型飞机又分为中型一和中型二, 具体分类如下:中型一质量为7~70 t(如B737-300, B737-700)、中型二质量为70~136 t(如B757-200, A320)和重型质量大于136 t(如B747-400, A330)。通过飞机起飞/降落所产生的噪声事件时序数据对当前飞机标记进行判断。机场噪声事件时序数据定义为左波段、中波段和右波段3个波段。图2给出NMT13噪声监测点的3种机型噪声事件的波形图, 其中图2(a)是噪声事件的左波段, 可以对应到飞机的发动机预启动阶段, 噪声值比较平稳, 并从正常噪声值开始呈现略微的上升趋势。图2(b)是噪声事件的中波段, 噪声值先陡峭上升, 到达某一峰值后又快速下降, 可以对应到飞机加速起飞以及爬升远离机场的阶段, 从图中可以得出, 重型飞机的噪声值大于中型一和中型二飞机的噪声值。图2(c)是噪声事件的右波段, 噪声值比较平稳, 并呈现下降略微下降趋势, 最终回落到正常噪声值范围。

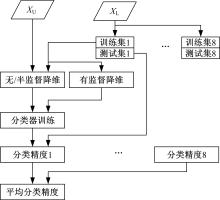
图2 NMT13的三种机型平均噪声波形对比Fig.2 Average noise wave pattern of three aircraft models in the NMT13

3.2 实验过程设置

为了验证SLFisher降维后对机型识别的性能, 选取了另外4种对比算法, 其中欧式距离[10]和动态时间规整[19]两种距离度量方式直接对噪声事件的时序数据进行分类, 主成分分析(PCA)[11]、线性判别分析(LDA)[18]和半监督局部Fisher(SLFisher)[17]对降维后的数据进行分类。SLFisher、PCA和LDA降维后的维度可以预先设定或是由特征值比率决定, 后者γ = ∑j∈dλ j/ ∑i∈Dλ i, 其中 λi和 λj是降序排序的第i和第j个特征值(λ1≥λ2≥⋯≥λD),D是机场噪声事件时序数据的原始高维度,d)是机场噪声事件时序数据的降维得到的低维度, 并且 d< D。在此设定降维的特征值比率为95%或低维度 d=30, 对于该值的设定既可以满足机场噪声事件时间序列降维的需求, 又可以去除时间序列中非重要的特征信息。通过后续实验, 验证了低维度机场噪声数据能够快速而有效地完成后续处理。

图3 降维评估框架Fig.3 Framework of dimensionality evaluation

由于 k最近邻分类算法是一个理论上比较成熟, 并且是最简单的机器学习算法之一, 通常用来评估其他算法执行效果。本文实验中采用1最近邻分类器对时间序列或降维数据进行分类, 采用精度评估上面5种算法的性能。具体的降维评估框架如图3所示。对于每个机场噪声事件的时间序列数据集, 每个算法均重复实验10次8重交叉验证, 分别抽取其中一个月的数据作为无机型标记数据 XU, 其余数据作为有机型标记数据 XL。无监督PCA和半监督SLFisher都是在所有数据上进行降维, 主要区别是, 前者丢弃有标记数据的类别信息, 直接将所有数据作为无标记数据进行降维, 而后者既利用有标记数据的类别信息, 又充分地考虑无标记数据的分布信息进行降维。另外, 有监督LDA仅仅利用部分有标记数据, 而舍去无标记数据的降维。算法最终的评估结果, 取1NN平均值作为算法最终分类精度。

3.3 实验结果

表2给出机场噪声事件的时间序列数据在5种算法上的1近邻分类结果, 其中, Euc.是欧式距离的缩写符合。从表2中得出, SLFisher算法进行机场噪声的时间序列数据降维再分类, 获得的分类效果均优于其他算法。与Euc.、DTW、PCA和LDA的平均精度相比, SLFisher的平均精度分别提高了23.37%、21.85%、19.04%和5.77%。

表2 机场噪声事件的1NN分类精度比较 Table 2 Comparison of 1NN classification accuracy in the airport-noise event

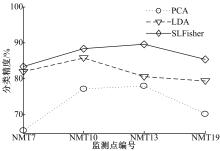
图4 三种降维算法的分类精度对比Fig.4 The comparison of classification accuracies of three dimensionality methods

图4为PCA、LDA和SLFisher三种降维算法在机场噪声事件时间序列数据上得到的分类精度对比图。由图4可知, 仅使用有标记数据的LDA降维的分类精度优于PCA降维的分类精度, 原因在于从某一分布的数据中随机抽取部分数据作为无标记数据, 其余的数据作为有标记数据, 这两部分数据的整体分布依然存在。对于有标记数据的影响而言, 则是数据的采样率降低, 即本实验中LDA优于PCA, 半监督SLFisher降维的分类精度为最优。

由表2和图4的结果可以归纳出如下三点:①波形相似性的动态时序规整度量并不总优于欧式距离度量, 原因在于动态时序规整度量通过扭曲波形的方式计算两个波形的相似性, 虽然对于偏移的相似波形能够得到很好效果, 但是对于本来非相似的波形通过DTW度量会产生不利的影响; ②利用数据标记信息的有监督降维算法优于无监督降维算法, 其原因在于标记信息作为数据的一部分, 当有标记数据量足够多时, 标记信息能够在降维过程中起指导数据降维的作用; ③半监督降维算法能结合有标记和无标记数据, 取得的降维效果优于无监督和有监督降维算法。

4 结束语

将SLFisher算法引入时间序列降维中, 并在机场噪声事件数据上完成降维和机型识别。该算法通过重构概率类使得无标记数据获得一个所属标记的概率, 数据对权值实现多模态分布数据距离的差异化, 以及不相关判别向量优化Fisher准则函数, 最终实现从半监督降维后的类间数据对尽可能地分离、类内邻近数据对尽可能地紧凑且类内非邻近数据距离保持相对不变。最后, 引用机场噪声事件作为时间序列数据的案例作为实验数据集, 验证了SLFisher算法能够在极大地降低机场噪声事件的时间序列数据维度的同时, 可以保留时间序列数据中区别不同类别的内在本质的特征, 并由 k最近邻分类算法的机型识别精度得出, SLFisher降维的准确率优于参与比较的PCA和LDA算法。

The authors have declared that no competing interests exist.

参考文献
[1] Fu T. A review on time series data mining[J]. Engineering Applications of Artificial Intelligence, 2011, 24(1): 164-181. [本文引用:1]
[2] Batista G E, Wang X, Keogh E J. A complexity-invariant distance measure for time series[C]∥Proceedings of the 2011 SIAM International Conference on Data Mining, 2011, 11: 699-710. [本文引用:1]
[3] Esling P, Agon C, Time-series data mining[J]. ACM Computing Surveys (CSUR), 2012, 45(1): 1-12. [本文引用:1]
[4] Wang X, Mueen A, Ding H, et al. Experimental comparison of representation methods and distance measures for time series data[J]. Data Mining and Knowledge Discovery, 2013, 26(2): 275-309. [本文引用:1]
[5] 吴红花, 刘国华, 王伟. 不确定时间序列的相似性匹配问题[J]. 计算机研究与发展, 2014, 51(8): 1802-1810.
Wu Hong-hua, Liu Guo-hua, Wang Wei. Similarity matching for uncertain time series[J]. Journal of Computer Research and Development, 2014, 51(8): 1802-1810. [本文引用:1]
[6] Scott S, Varian H. Predicting the present with bayesian structural time series[J]. International Journal of Mathematical Modelling and Numerical Optimisation, 2014, 5(1): 4-23. [本文引用:1]
[7] Keogh E, Chakrabarti K, Pazzani M, et al. Dimensionality reduction for fast similarity search in large time series databases[J]. Knowledge and Information Systems, 2001, 3(3): 263-286. [本文引用:1]
[8] Chakrabarti K, Keogh E, Mehrotra S, et al. Locally adaptive dimensionality reduction for indexing large time series databases[J]. ACM Transactions on Database Systems, 2002, 27(2): 188-228. [本文引用:1]
[9] Xing E P, Jordan M I, Russell S, et al. Distance metric learning with application to clustering with side-information[J]. Advances in Neural Information Processing Systems, 2003: 15: 505-512. [本文引用:1]
[10] 邹朋成, 王建东, 杨国庆, 等. 辅助信息自动生成的时间序列距离度量学习[J]. 软件学报, 2013, 24(11): 2642-2655.
Zou Peng-cheng, Wang Jian-dong, Yang Guo-qing, et al. Distance metric learning based on side information autogeneration for time series[J]. Journal of Software, 2013, 24(11): 2642-2655. [本文引用:2]
[11] Jolliffe I. Principal Component Analysis[M]. USA: John Wiley & Sons, 2005. [本文引用:3]
[12] Abdi H, Williams L J. Principal component analysis[J]. Wiley interdisciplinary reviews: computational statistics, 2010, 2(4): 433-459. [本文引用:1]
[13] Lin J, Keogh E, Lonardi S, et al. A symbolic representation of time series, with implications for streaming algorithms[C]∥ACM SIGMOD Workshop on Research Issues in Data Mining and Knowledge Discovery, San Diego, USA, 2003: 2-11. [本文引用:1]
[14] Lin J, Keogh E, Wei L, et al. Experiencing SAX: a novel symbolic representation of time series[J]. Data Mining and Knowledge Discovery, 2007, 15(2): 107-144. [本文引用:1]
[15] Ahmed A, Bakar A, Hamdan A. Harmony search algorithm for optimal word size in symbolic time series representation[C]∥IEEE 2011 3rd Conference on Data Mining and Optimization, Bangi, Malaysia, 2011: 57-62. [本文引用:1]
[16] Park S, Kim S W, Chu W W. Segment-based approach for subsequence searches in sequence databases[C]∥Proceedings of the 2001 ACM Symposium on Applied Computing, New York, USA, 2001: 248-252. [本文引用:1]
[17] 王寅同, 王建东, 陈海燕, 等. 基于概率类和不相关判别的半监督局部Fisher方法[J]. 控制与决策, 2015, 30(1): 32-38.
Wang Yin-tong, Wang Jian-dong, Chen Hai-yan, et al. Semi-supervised local Fisher method based on probability class and uncorrelated discriminant[J]. Control and Decision, 2015, 30(1): 32-38. [本文引用:3]
[18] Fisher R. The Use of multiple measurements in taxonomic problems[J]. Annals of Eugenics, 1936, 7(2): 179-188. [本文引用:2]
[19] Sakoe H, Chiba S. Dynamic programming algorithm optimization for spoken word recognition[C]∥IEEE Transactioin on Acoustics, Speech and Signal Processing, 1978, 26(1): 43-49. [本文引用:2]
[20] Xi X, Keogh E, Shelton C, et al. Fast time series classification using numerosity reduction[C]∥In Process of the International Conference on Machine Learning, New York, USA, 2006: 1033-1040. [本文引用:1]
[21] Rakthanmanon T, Campana B J, Mueen A, et al. Searching and mining trillions of time series subsequences under dynamic time warping[C]∥In Process of the International Conference on Knowledge Discovery and Data Mining, New York, USA, 2012: 262-270. [本文引用:1]
[22] Keogh E. Exact indexing of dynamic time warping[J]. Knowledge and Information Systems, 2005: 7(3): 358-386. [本文引用:1]
[23] Shimodaira H, Noma K, Nakai M, et al. Dynamic time-alignment kernel in support vector machine[J]. Advances in Neural Information Processing Systems, 2002, 14: 921-928. [本文引用:1]
[24] Cuturi M, Vert J P, Birkenes O, et al. A kernel for time series based on global alignments[C]∥IEEE Computer Society on Acoustics, Speech and Signal Processing, Honolulu, HI, 2007: 413-416. [本文引用:1]
[25] Cuturi M. Fast global alignment kernels[C]∥In Process of the International Conference on Machine Learning, ACM, Bellevue, USA, 2011: 929-936. [本文引用:]