引用本文
王红梅, 党源源, 胡明, 刘大有. 基于排序树的频繁项集挖掘算法.吉林大学学报:工学版, 2016, 46(4): 1216-1221
WANG Hong-mei, DANG Yuan-yuan, HU Ming, LIU Da-you. Frequent itemsets mining algorithm based on sort tree. Journal of Jilin University Engineering and Technology Edition, 2016, 46(4): 1216-1221  
Permissions
Copyright©2016, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
基于排序树的频繁项集挖掘算法
王红梅1,2, 党源源1, 胡明1, 刘大有2,3
1.长春工业大学 计算机科学与工程学院,长春 130012
2.吉林大学 计算机科学与技术学院, 长春 130012
3.吉林大学 符号计算与知识工程教育部重点实验室,长春 130012
通讯作者：党源源(1980-),女,副教授.研究方向:数据挖掘,知识管理.E-mail:dang.yuanyuan@gmail.com

作者简介:王红梅(1968-),女,教授,博士研究生.研究方向:数据挖掘,智能计算.E-mail:wanghm@ccut.edu.cn

基金:国家自然科学基金项目(61133011); 吉林省自然科学基金项目(20101525)
摘要

提出了排序树的概念以及用排序树存储频繁项集的思想,证明了末项剪枝性质,以 O(1)的时间实现了与Apriori算法同样的连接和剪枝操作,采用祖先兄弟表示法存储排序树,在某事务不包含祖先时跳过具有共同祖先的所有兄弟结点,提高了计算支持度的时间性能。理论分析和实验结果均表明,在时间性能方面本文算法与Apriori算法相比有较大提高。

关键词: 人工智能; 频繁项集; 末项剪枝; 排序树; 祖先兄弟表示
中图分类号:TP311 文献标志码:A 文章编号:1671-5497(2016)04-1216-06
Frequent itemsets mining algorithm based on sort tree
WANG Hong-mei1,2, DANG Yuan-yuan1, HU Ming1, LIU Da-you2,3
1.School of Computer Science and Engineering, Changchun University of Technology, Changchun 130012,China
2.College of Computer Science and Technology, Jilin University, Changchun 130012,China
3.Key Laboratory of Symbolic Computation and Knowledge Engineering of Ministry of Education,Jilin University,Changchun 130012, China
Abstract

In this paper, the concept of sort tree is proposed, and the sort tree is used to store frequent itemsets, which proves the property of the last item pruning. Joining and pruning operations a re implemented as Apriori algorithm with O(1) time complexity. Ancestor-brother express is used to store the sort tree. If an ancestor does not exist in a transaction, all the brother nodes with the same ancestor will be skipped. So the time performance of counting support can be improved. Theoretical analysis and experimental results show that the proposed algorithm can improve the time performance greatly compared with Apriori algorithm.

Keyword: artifical intelligence; frequent itemsets; last term pruning; sort tree; ancestor-brother express
0 引 言

在大数据时代, 数据处理的一个重要转变就是从追求因果关系中解脱出来, 将注意力放在相关关系的发现和使用上[1]。频繁项集挖掘能够发现大型事务数据集中反复出现的相关联系, 是当前的研究热点之一, Apriori[2]和FP-Growth[3]是两个基本的频繁项集挖掘算法, 近年来, 虽有很多频繁项集挖掘算法被提出, 但大多是这两个算法的改进或扩展。

Apriori算法的基本原理是用频繁k-项集找出频繁(k+1)-项集, 为提高逐层扫描的效率, Apriori算法利用了Apriori性质, 即频繁项集的所有非空子集都是频繁的。很多学者对Apriori算法进行了改进研究, 如文献[4]采用散列表压缩存储候选项集并增加统计数, 提高了计算支持度的时间性能; 文献[5]将数据集划分为用开始点标记的块, 可以动态评估已计数的所有项集的支持度; 文献[6]提取候选模式的紧密上阶, 从而减少对数据集的扫描; 文献[7]提出分段计算支持度的思想, 缩减了潜在项集的规模; 文献[8]将数据集按照首项划分为数据子集并采用分组索引表存储, 减少了对数据集扫描的时间代价。

FP-Growth算法的基本原理是将数据集压缩存储到频繁模式树(Frequent-pattern tree, FP-树)中, 然后递归地对FP-树进行挖掘。基于FP-树框架的算法有很多, 其中H-Mine算法[9]构建了基于数组的H-Struct结构, 采用分片方法, 使得每一片都能装入内存。OP算法[10]集成了模式增长树和FP树, 以自顶向下和自底向上方式遍历树。文献[11]在FP-树上使用基于投影进行超集检测的机制, 减少了遍历树的开销。文献[12]采用带项目头表的FP-树存储数据集, 解决了当支持度阈值发生变化时最大频繁项集的更新挖掘问题。文献[13]将约简划分后的数据集压缩存储到AFOPT树中, 通过遍历AFOPT树替代原数据集来挖掘频繁项集。

Apriori算法使用逐层搜索的迭代方法, 每次迭代都要执行以下操作:①连接操作, 判断两个k-项集是否前k-1项相同且第k项不同, 从而产生候选频繁(k+1)-项集; ②剪枝操作, 应用Apriori性质剪掉存在非频繁k-项子集的候选频繁(k+1)-项集, 从而得到精简的候选频繁(k+1)-项集; ③扫描数据集, 计算候选频繁(k+1)-项集的支持度。这些操作都非常耗时, 因此, 几乎所有的类Apriori算法都试图在上述3个操作方面有所突破。本文提出了频繁项集排序树(以下简称排序树)的概念以及采用排序树存储频繁项集的思想, 在此基础上提出了基于排序树的频繁项集挖掘算法(Frequent itemsets mining algorithm based on sort tree, FIMST)。证明并应用了末项剪枝性质, 使得在排序树上能够以O(1)的时间实现与Apriori算法同样的连接和剪枝操作, 采用祖先兄弟表示法存储排序树, 在某事务不包含祖先时, 跳过具有共同祖先的所有兄弟结点对应的候选频繁项集, 从而提高了计算支持度的时间性能。并且在连接和剪枝操作、计算支持度等方面, 将FIMST算法与其他算法进行了对比分析。

1 基本概念

定义1[14] 设I={I1, I2, …, Im}是所有项的集合, 事务数据集T={T1, T2, …, Tn}, 事务Ti(1≤ i≤ n)是一个二元组< TID, B> , 其中TID为事务的标识号, B为非空项集。事务数据集的示例如表1所示。

表1 事务数据集示例 Table 1 An example of transaction data sets

定义2[14] 项集中包含的所有项的个数称为项集的长度, 长度为k的项集记为k-项集。可以按项集中项的序号来引用每个项, 例如, A[i]表示k-项集A中的第i项(1≤ i≤ k)。

定义3[14] 在事务数据集T中, 当且仅当A⊆B, 元组< TID, B> 包含项集A。数据集T包含项集A的元组的个数, 称为项集A在数据集T中的支持度, 记为sup_count(A)。给定支持度阈值min_sup, 如果项集A满足sup_count(A)≥ min_sup, 则称项集A为事务数据集T的一个频繁项集, 频繁k-项集的集合通常记为Lk。

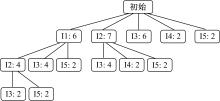
定义4 频繁项集排序树是满足下列条件的树结构:①根结点表示挖掘的初始状态; ②除了根结点外, 其他每个结点标识为[项:支持度]; ③对于某个结点A, 由根结点到该结点经过的结点集合(根结点除外)组成一个频繁项集, 该项集的支持度即为结点A的支持度; ④除了根结点外, 每个结点的支持度均不小于阈值min_sup; ⑤分支结点的所有孩子结点按字典次序自左向右升序排列。

对于表1所示数据集, 图1是给定支持度阈值min_sup=2的排序树。显然, 随着min_sup的增加, 排序树的规模将大大减小。

图1 给定min_sup=2的排序树Fig.1 Sort tree of min_sup=2

定义5 规定排序树的根结点为第0层, 对其余任何结点, 若某结点在第k层, 则其孩子结点在第k+1层, 排序树中所有结点的最大层数称为排序树的深度。

性质1 排序树的深度等于事务数据集T中频繁项集的最大长度。

证明 设排序树的深度为k, 从根结点到第k层的某个结点(显然, 第k层的所有结点均是叶子结点)经过的所有结点组成频繁项集{A[1], A[2], …, A[k]}, 则该项集的长度为k, 下面证明事务数据集T中不存在长度大于k的频繁项集, 采用反证法。

假设数据集T中存在长度为k+1的频繁项集{B[1], B[2], …, B[k+1]}, 由排序树的定义, 树中一定存在一条路径, 该路径经过的结点集合是{B[1], B[2], …, B[k+1]}, 其路径长度为k+1, 则结点B[k+1]在排序树的第k+1层, 与排序树的深度为k产生矛盾, 从而结论成立, 证毕。

排序树以清晰的方式表达了以下信息:

(1)排序树只存储频繁项集, 且存储了所有频繁项集。

(2)将根结点到某个结点经过的结点收集起来, 得到该结点对应的频繁项集及其支持度。

(3)排序树的第k层结点表示所有频繁k-项集。

(4)排序树的深度表示最长的频繁项集。

性质2 对于排序树中第k层的结点A和B, 结点A表示的频繁项集为{A[1], A[2], …, A[k]}, 结点B表示的频繁项集为{B[1], B[2], …, B[k]}, 若结点B是结点A的右兄弟, 则有A[1]=B[1]∧ A[2]=B[2]∧ …∧ A[k-1]=B[k-1]∧ A[k]< B[k]成立。

证明 由于结点B是结点A的右兄弟, 则它们具有相同的祖先结点, 即A[1]=B[1]∧ A[2]=B[2]∧ …∧ A[k-1]=B[k-1], 换言之, 频繁项集A和B具有相同的最大前缀; 由排序树的定义, 有A[k]< B[k], 因此结论成立, 证毕。

定义6 在排序树中, 若结点B是结点A的右兄弟, 则称结点A和B是可连接的, 记为A 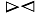B, 如果连接后的项集是频繁的且支持度为t, 则为结点A增加一个孩子结点, 并将该结点标识为[B, t]。

由性质2和定义6, 在排序树中执行连接操作, 无须判断两个k-项集是否前k-1项相同且第k项不同, 直接将兄弟结点进行连接即可。

性质3(末项剪枝性质) 设TR为排序树的根结点, 结点A对应频繁k-项集{A[1], A[2], …, A[k-1], A[k]}, 结点B对应频繁k-项集{B[1], B[2], …, B[k-1], B[k]}, 且结点B是结点A的右兄弟, 如果排序树中不存在路径< TR, A[k], B[k]> , 则连接A和B得到的候选频繁(k+1)-项集一定非频繁。

证明 在排序树中, 连接结点A和B得到(k+1)-项集{A[1], A[2], …, A[k-1], A[k], B[k]}, 如果排序树中不存在路径< TR, A[k], B[k]> , 则末项子集{A[k], B[k]}非频繁, 根据Apriori性质, 项集{A[1], A[2], …, A[k-1], A[k], B[k]}一定非频繁, 从而结论成立, 证毕。

定理1 对频繁k-项集Lk执行连接操作得到候选频繁(k+1)-项集Ck+1, 设C'k+1⊆Ck+1且C'k+1中的项集存在非频繁k-项子集, C″k+1⊆Ck+1且C″k+1中的项集存在非频繁末项子集, 则Ck+1-C'k+1=Ck+1-C″k+1。

证明 对于任意lk+1∈ Ck+1且lk+1=A 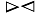B, 则lk+1={A[1], A[2], …, A[k-1], A[k], B[k]}, 在lk+1的所有k-项子集中, 项集{A[1], A[2], …, A[k-1], A[k]}和项集{A[1], A[2], …, A[k-1], B[k]}一定是频繁的, 设a[1]a[2]…a[k-2]⊂A[1]A[2]…A[k-1], 则余下的k-项子集为{a[1], a[2], …, a[k-2], A[k], B[k]}, 根据Apriori性质, 项集{a[1], a[2], …, a[k-2], A[k]}和项集{a[1], a[2], …, a[k-2], B[k]}一定是频繁的, 则当且仅当末项子集{A[k], B[k]}是频繁的, {a[1], a[2], …, a[k-2], A[k], B[k]}是频繁的, 换言之, 若lk+1中存在非频繁的k-项子集, 则lk+1中一定存在非频繁的末项子集; 反之亦然。因此, 结论成立, 证毕。

由性质3和定理1, 在排序树中执行剪枝操作, 只须判断执行连接操作的兄弟结点在排序树中是否存在从根结点开始, 并且长度为2的路径, 无须判断其所有k-项子集是否频繁, 即可完成与Apriori算法同样的剪枝操作。例如, 在图1所示排序树中, 将第2层的兄弟结点[I3:4]和[I5:2](其双亲均是[I1:6])执行连接操作, 得到候选频繁3-项集{I1, I3, I5}, 由于排序树中没有路径< TR, I3, I5> , 则对{I1, I3, I5}执行剪枝。

2 本文算法(FIMST)
2.1 存储结构

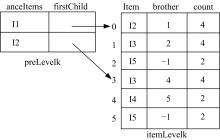
采用祖先兄弟表示法存储排序树, 祖先是排序树中兄弟结点的最长公共前缀。例如, 图1所示排序树第2层的存储示意图如图2所示。

图2 排序树的存储结构Fig.2 Storage structure of sort tree

其中, 在数组preLevelk中, anceItems存储祖先结点对应的项集; firstChild存储具有共同祖先的第一个孩子结点。在数组itemLevelk中, item存储某结点对应的项; brother存储该结点的右兄弟在数组itemLevelk中的下标; count存储该结点对应项集的支持度。

2.2 算法描述

FIMST算法的执行过程即构造排序树的过程, 设TR表示排序树的根结点, 对于排序树中的某个结点A, 设A.child表示结点A的孩子结点; A.rightsib表示结点A的右兄弟结点。给定支持度阈值min_sup, FIMST算法的具体描述如下:

算法:FIMST

输入:数据集T; 项的全集I; 阈值min_sup

输出:排序树TR

(1) ∥为排序树添加第1层结点

for each t∈ T

for each l∈ t

l.count++;

for each l∈ I

if (sup_count(l)≥ min_sup)

TR.child=[l, sup_count(l)];

(2) ∥为排序树添加第2层结点

for each {< A, B> |A.rightsib=B}

{

c=A 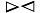B; add c to C2;

}

for each t∈ T

for each c∈ C2

if (c[1]∈ t and c[2]∈ t)

c.count++;

for each c∈ C2

if (sup_count(c)≥ min_sup)

c[1].child=[c[2], sup_count(c)];

}

(3) k=2;

(4) ∥为排序树添加第k+1层结点

flagt=0; ∥初始化标志, Lk+1为空集

for each {< A, B> |A.rightsib=B}

if (TR.child==A∧ A.child==B) {

c=A 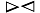B; add c to Ck+1;

} ∥else执行剪枝

for each t∈ T ∥扫描数据集, 计算支持度

for each ct∈ preLevelk

if (ct.anceitems⊂t) {

c=ct.firstChild;

do

{

if (c.item∈ t) c.count++;

c=c.brother;

}while (c.brother!=-1);

} //else跳过共同祖先的兄弟对应项集

for each c∈ Ck+1

if (sup_count(c)≥ min_sup) {

flag=1;

c[k].child=[c[k+1], sup_count(k)];

}

if (flag==0) Lk+1为空集, 算法结束;

(5) k=k+1; 转步骤(4)继续构造排序树。

2.3 算法的性能分析

(1)连接操作。Apriori算法需要判断两个k-项集是否前k-1项相同且第k项不同, 其时间复杂度为O(k)。由于排序树中的兄弟结点具有共同的最大前缀, 因此, FIMST算法可以直接将兄弟结点执行连接操作, 其时间复杂度为O(1)。

(2)剪枝操作。Apriori算法需要判断(k+1)-项集的k-项子集是否频繁, 最坏情况下的时间复杂度为O(k× |Lk|)。FIMST算法应用末项子集剪枝性质, 只需在排序树中从根结点出发查找长度为2的路径, 其时间复杂度为O(1)。

(3)计算支持度。Apriori算法在扫描数据集时, 需要依次判断每个候选频繁(k+1)-项集是否包含在元组中, 设元组个数为n, 其时间复杂度为O(n× |Ck+1|)。FIMST算法先判断祖先是否包含在元组中, 若包含, 则只需判断候选(k+1)-项集的第k+1项是否在元组中; 否则跳过具有该祖先的所有兄弟结点对应的候选频繁(k+1)-项集, 从而减少了计算支持度的时间消耗, 其时间性能取决于具体的数据集以及候选频繁(k+1)-项集。

3 实验验证

为进一步验证FIMST算法的有效性, 本文在CPU Intel Core(TM)2、主频1.86 GHz、2 G内存主机上, 基于Windows XP系统在Visual C++ 6.0编程环境下, 分别实现了Apriori算法、FP-Growth算法和本文算法(FIMST)。图3(a)给出了在FIMI数据集T10I4D100k上的实验结果, 该数据集包含870个项; 100 000条事务; 事务平均长度为10。图3(b)给出了在almaden数据集T10I4D100k上的实验结果, 该数据集包含1000个项; 100 000条事务; 事务平均长度为10。图3(c)给出了在FIMI数据集Mushroom上的实验结果, 该数据集包含120个项; 8124条事务; 事务长度均为23。

图3 不同算法实验结果对比Fig.3 Result comparison among different algorithms

FIMI-T10I4D100k和almaden-T10I4D100k均是不等长稀疏数据集, FIMI-Mushroom是等长稠密数据集, 实验结果表明, 无论稀疏或稠密的数据集, FIMST算法的时间消耗均低于Apriori算法和FP-Growth算法。

4 结束语

提出了基于排序树的频繁项集挖掘算法FIMST, 充分利用了树结构的性质:在排序树上执行连接操作不产生时间消耗; 执行剪枝操作消耗常数时间。利用排序树共享祖先结点的特点, 使得FIMST算法具有较好的时间性能。排序树在保存频繁(k+1)-项集时, 共享了频繁k-项集的结点空间, 而且无需存储候选频繁项集, 使得FIMST算法具有良好的空间性能。FIMST算法以清晰的方式展现了频繁项集的挖掘过程, 没有复杂的理论推导, 易于理解、实现以及程序优化。本文提出的排序树可以存储、更新、维护和管理已挖掘出来的频繁项集, 使得挖掘出的知识更有使用价值, 此外, 排序树还具有适合处理超大型事务数据集和分布式数据集、可变支持度阈值、可并行计算等优势, 这对于解决现实应用领域的频繁项集挖掘问题具有较大价值。

The authors have declared that no competing interests exist.

参考文献
[1] Schonberger V M, Cukier K. Big Data[M]. Eamon Dolan/Houghton Mifflin Harcourt, 2013. [本文引用:1]
[2] Agrawal R, Srikant R. Fast algorithms for mining association rules[C]∥Proc of the Int'l Conf on Very Large Data Bases, Santiago, Chile, 1994: 487-499. [本文引用:1]
[3] Han J, Pei J, Yin Y. Mining frequent patterns without cand idate generation[C]∥Proc of the Int'l Conf on Management of Data, Dallas, TX, 2000: 1-12. [本文引用:1]
[4] Park J S, Chen M S, Yu P S. An effective hash-based algorithm for mining association rules[C]∥Proc of the Int'l Conf on Management of data, San Jose, 1995: 175-186. [本文引用:1]
[5] Brin S, Motwani R, Ullman J D, et al. Dynamic itemset counting and implication rules for market basket analysis[C]∥Proc of the Int'l Conf on Management of Data, Tucson, AZ, 1997: 255-264. [本文引用:1]
[6] Geerts F, Goethals B, Bussche J. A tight upper bound on the number of cand idate patterns[C]∥Proc of the Int'l Conf on Data mining, San Jose, CA, 2001: 155-162. [本文引用:1]
[7] 李雄飞, 苑森淼, 董立岩, 等. 多段支持度数据挖掘算法研究[J]. 计算机学报, 2001, 24(6): 661-665.
Li Xiong-fei, Yuan Sen-miao, Dong Li-yan, et al. A data mining algorithm based on calculating multi-segment support[J]. Chinese Journal of Computers, 2001, 24(6): 661-665. [本文引用:1]
[8] 王红梅, 胡明. 基于散列的频繁项集分组算法[J]. 计算机应用, 2013, 33(11): 47-51.
Wang Hong-mei, Hu Ming. Frequent itemsets grouping algorithm based on hash[J]. Journal of Computer Applications, 2013, 33(11): 47-51. [本文引用:1]
[9] Pei J, Han J, Lakshmanan L V S. Mining frequent itemsets with convertible constraints[C]∥Proc of the Int'l Conf on Data Engineering, Heidelberg, Germany, 2001: 324-332. [本文引用:1]
[10] Liu J, Pan Y, Wang K, et al. Mining frequent item sets by opportunistic projection[C]∥Proc of the Int'l Conf on Knowledge Discovery in Databases, Edmonton, Canada, 2002: 23-32. [本文引用:1]
[11] 颜跃进, 李舟军, 陈火旺. 基于FP-Tree有效挖掘最大频繁项集[J]. 软件学报, 2005, 16(2): 215-222.
Yan Yue-jin, Li Zhou-jun, Chen Huo-wang. Efficiently mining of maximal frequent item sets based on FP-tree[J]. Journal of Software, 2005, 16(2): 215-222. [本文引用:1]
[12] 杨君锐, 杨莉. 分布式全局最大频繁项集更新挖掘算法[J]. 华中科技大学学报: 自然科学版, 2011, 39(12): 85-88.
Yang Jun-rui, Yang Li. Algorithm of updating mining for distributed global maximal frequent itemsets[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2011, 39(12): 85-88. [本文引用:1]
[13] 毛宇星, 陈彤兵, 施伯乐. 一种高效的多层和概化关联规则挖掘方法[J]. 软件学报, 2010, 22(12): 2965-2980.
Mao Yu-xing, Chen Tong-bing, Shi Bo-le. Efficient method for mining multiple-level and generalized association rules[J]. Journal of Software, 2010, 22(12): 2965-2980. [本文引用:1]
[14] Han J, Cheng H, Xin D, et al. Frequent pattern mining: current status and future directions[J]. Data Mining and Knowledge Discovery, 2007, 15(1): 55-86. [本文引用:3]