压缩编码孔径红外成像超分辨重建

引用本文

王新华, 欧阳继红, 庞武斌. 压缩编码孔径红外成像超分辨重建.吉林大学学报:工学版, 2016, 46(4): 1239-1245
WANG Xin-hua, OUYANG Ji-hong, PANG Wu-bin. Supper-resolution reconstruction of infrared images of compressive coded aperture. Journal of Jilin University Engineering and Technology Edition, 2016, 46(4): 1239-1245 复制到剪切板

Permissions

压缩编码孔径红外成像超分辨重建

王新华^1,², 欧阳继红¹, 庞武斌²

1.吉林大学计算机科学与技术学院,长春 130012

2.中国科学院长春光学精密机械与物理研究所应用光学国家重点实验室,长春 130033

通讯作者：欧阳继红(1964-),女,教授,博士生导师.研究方向:空间推理与数据挖掘.E-mail:ouyj@jlu.edu.cn

作者简介:王新华(1984-),男,工程师,博士研究生.研究方向:计算光学与机器视觉.E-mail:xinhuajlu@163.com

基金:国家自然科学基金项目(61170092,61133011)

摘要

为了利用低分辨率红外探测器获取高质量图像信息,对基于频谱面的压缩编码孔径成像方法和超分辨率图像重建算法进行了研究。首先,在频谱面加入孔径编码器,通过傅里叶变换对采样图像信号进行编码压缩。然后,利用光学成像系统的分片光滑性,实现信号在傅里叶变换域的稀疏表示。最后,提出了两点步长梯度法与自适应非单调线搜索策略相结合的梯度投影并行加速算法,用于完成对稀疏信号的超分辨重建。实验结果表明,该算法能够以远小于原始信号的数据量重建出高分辨率图像信息。

关键词: 计算机应用; 压缩感知; 编码孔径; 超分辨重建

中图分类号:TP394.1 文献标志码:A 文章编号:1671-5497(2016)04-1239-07

Supper-resolution reconstruction of infrared images of compressive coded aperture

WANG Xin-hua^1,², OUYANG Ji-hong¹, PANG Wu-bin²

1.College of Computer Science and Technology, Jilin University, Changchun 130012, China

2. State Key Laboratory of Applied Optics,Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033, China

Abstract

In order to obtain high quality image information using infrared detector with low resolution, a compressive coded aperture imaging method based on the frequency spectrum plane and the Supper Resolution Image Reconstruction (SRIR) algorithm was investigated. First, the aperture encoder was added to the frequency spectrum plane, and the image sampling signal was compressive coded by Fourier transform. The, by virtue of the piecewise smooth of the optimal imaging system, the signal sparse representation was realized based on Fourier transform domain. Finally, the SRIR of the sparse signal was completed by improved Gradient Projection for Sparse Reconstruction (GPSR) parallel acceleration algorithm, which combined with GPSR-BB algorithm and adaptive non-monotone line search strategy. Experimental results indicate that the high resolution images can be constructed with information far less than that of the original signal.

Keyword: computer application; compressed sensing; coded aperture; super resolution image reconstruction (SRIR)

Show Figures

焦平面探测器是影响红外成像分辨率的核心器件, 因其结构异常复杂, 从硬件角度提高探测器分辨率难度极大。如何利用探测器有限的资源获取高质量的图像信息成为一个亟待解决的技术瓶颈。压缩感知(Compressed sensing, CS)理论的提出突破了传统奈奎斯特采样定理的限制^[1], 使得通过低分辨率探测器获取高分辨率图像信息成为可能。近些年, CS理论在压缩成像、医疗成像和雷达成像等领域得到了广泛的应用^{[2, 3, 4]}, 比较有代表性的成果是美国Rice大学研制的单像素相机^[5], 此外文献[6]详细阐述了光学压缩成像系统研究进展, 并对今后面临的挑战性问题进行了探讨。

针对红外成像系统分辨率低、信号受噪声干扰严重等问题, 基于CS理论提出了压缩编码孔径红外成像超分辨重建方法。首先, 在频谱面加入孔径编码器, 通过傅里叶变换对采样图像信号进行编码压缩和稀疏表示。然后, 采用两点步长梯度法与自适应非单调线搜索策略相结合的梯度投影稀疏重构并行加速算法, 完成对欠采样信号的超分辨重建。实验结果表明, 该方法能够以远小于原始信号的数据量重建出高分辨率的图像信息, 并表现出较好的实时性, 具有一定的工程应用价值。

1 压缩感知理论基本原理

CS理论的基本原理是只要信号在某个正交变换空间具有稀疏性, 就能以较低的频率 $\begin{matrix} (M \leq N) 采样信号, 而且可能以高概率重构该信号。如图 1 所示, 首先, 如果长度为 N 的信号 X \in R^{N} 在某个正交基 Ψ 上具有 K 稀疏表示; 其次, 设计一个与 Ψ 不相关的 M \times N 维观测矩阵 Φ, 用观测矩阵 Φ 观测原信号得到 M 个观测值, 其中 K < M ≪ N, 得到观测值 Y, 那么可以利用最优化方法从观测值中高概率重构 X 。 \end{matrix}$

	Figure Option View Download New Window
	图1 压缩传感原理图Fig.1 Principle of compressed sensing

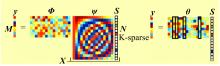
压缩传感方程为 y=ΦX=ΦΨs=Θs,将原来的观测基矩阵Φ变换为Θ=ΦΨ(称之为传感矩阵),解出s逼近值s',则重构后原信号为X'=Ψs'。

压缩传感理论涉及以下几个方面^[7]:

(1)信号的稀疏表示。只有信号是K稀疏的,才有可能在观测M个观测值时,根据K个较大的系数重建原始长度为N)的信号。稀疏表示方法包括:多种变换域分析方法和冗余字典学习方法等。

(2)观测矩阵的设计。观测矩阵Φ与稀疏矩阵Ψ的乘积满足RIP性质(有限等距性质), 这个性质保证了观测矩阵不会把两个不同的K稀疏信号映射到同一个集合中。对于K稀疏的原始信号s,存在实数δ_k∈(0,1),)使得式(1)成立:

$\begin{matrix} (1 - δ_{k}) ‖ s ‖_{2}^{2} \leq ‖ ΦΨs ‖_{2}^{2} \leq (1 + δ_{k}) ‖ s ‖_{2}^{2} (1) \end{matrix}$

观测矩阵 Φ与稀疏矩阵Ψ的乘积满足RIP性质。观测矩阵选取的原则如下:①观测矩阵Φ与稀疏矩阵Ψ的乘积满足RIP性质, 这就要求矩阵 Φ与矩阵Ψ最好不相关;②观测矩阵Φ对应物理硬件,因此观测矩阵Φ的选取必须易于硬件实现; ③矩阵 Φ与矩阵Ψ最好不相关;②观测矩阵Φ对应物理硬件,因此观测矩阵Φ是一个性质非常好的观测矩阵, 光学成像中, DMD对应于该矩阵的硬件实现。

(3)重构算法的设计。信号重构过程一般转换为一个最小 $\begin{matrix} L_{0} 范数的优化问题, 求解方法主要有最小 L_{1} \end{matrix}$ 范数法、匹配追踪系列算法和迭代阈值算法等。重构是基于如下严格的数学最优化问题, 可以写成式(2):

$\begin{matrix} \min ‖ s - Φ Ψ^{H} \hat{y} ‖_{2} + λ ‖ \hat{y} ‖_{0} (2) \end{matrix}$

式中: $\begin{matrix} \min ‖ \hat{y} ‖_{0} 为目标函数, 且满足等式约束 Φ Ψ^{H} \hat{y} = s 。 \end{matrix}$

2 编码孔径成像方法

2.1 编码孔径成像原理

Willett等^[8]提出了基于CS理论的采用频谱编码的方法, 利用大于探测器分辨率的相位板对图像傅里叶频谱进行编码, 探测器记录编码后的图像信息, 通过重构算法可以恢复得到一个与相位板分辨率一样的红外图像。

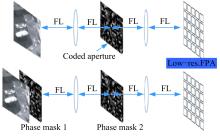
	Figure Option View Download New Window
	图2 编码孔径成像原理Fig.2 Principle of coded aperture imaging

如图2所示, 在红外成像的傅里叶频谱面加入孔径编码器, 编码器可以是空间光调制器或掩膜版, 在此过程中编码器会对光场中的高频成分进行编码, 被编码的频率带宽远大于探测器的奈奎斯特频率带宽, 只要通过合适的重构算法, 就可以恢复出高于探测器频率的红外图像, 也就是利用低频率的探测器实现了高频率的图像恢复。在硬件实现上, 在成像系统的频谱面上设置编码板, 编码板可以采用石英基地上镀铬, 然后用光刻的方法制作编码图案。

2.2 编码孔径矩阵设计

CS理论下的编码孔径成像, 探测器观测到的图像信号的表达式为:

$\begin{matrix} Y = R \times f = D (f \times A) \end{matrix}$

式中:R为观测矩阵;f为图像原始信号;D为欠采样操作;A为编码孔径矩阵,其中A的表达式为:

$\begin{matrix} A = F^{- 1} C_{p} F \end{matrix}$

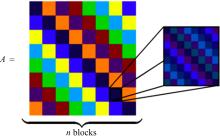
式中:F^(-1) 为傅立叶逆变换;C_p 为光学传递函数;F为傅立叶变换。如图3所示,矩阵A具有行元素循环特性,对于具有行元素循环特性的矩阵,只要行中每个元素都来自于某一分布(如高斯分布、均匀分布等),则A可以以非常高的概率满足RIP条件。

	Figure Option View Download New Window
	图3 观测矩阵特征Fig.3 Feature of observation matrix

矩阵 $\begin{matrix} A \end{matrix}$ 为具有行元素循环特性的矩阵并满足如下条件:① $\begin{matrix} A \end{matrix}$ 可以以非常高的概率满足RIP条件; ② $\begin{matrix} R = DA \end{matrix}$ 可以以非常高的概率满足RIP条件; ③ $\begin{matrix} RW \end{matrix}$ 可以以非常高的概率满足RIP条件, 其中 $\begin{matrix} W \end{matrix}$ 为哈尔小波变换矩阵。

2.3 编码板的图案设计

编码板图案p是生成观测矩阵R的关键,同时也是成像系统硬件实现的核心器件,A可以以非常高的概率满足RIP性质,这个性质保证了观测矩阵不会把两个不同的K稀疏信号映射到同一个集合中。

编码板图案设计步骤如下:

Step1 用高斯分布函数随机生成矩阵A,因为矩阵A具有块循环性质, 实际只需要生成一行元素, 其他只需要交替循环即可。

Step2 解线性方程 $\begin{matrix} A = F^{- 1} C_{p} F, 获得 C_{p} 。 \end{matrix}$

Step3 对 $\begin{matrix} C_{p} 作逆傅立叶变换求得编码板图案 P 。 \end{matrix}$

如图4所示, 计算得到的编码图案 $\begin{matrix} P \end{matrix}$ 必须具有物理实现性, 也就是可加工制作, 因此必须满足下述条件:①图案中每个元素必须是实数; ②图案中每个元素必须非负; ③图案中每个元素必须在区间[0, 1]内。

	Figure Option View Download New Window
	图4 编码板图案示意图Fig.4 Pattern of coded plane

从图4所示的图像数据采集过程可知, 利用压缩编码孔径成像方法可以有效降低数据采集量。

3 超分辨图像重建算法

3.1 图像重建问题描述

由于经过编码孔径成像系统所生成的数字信号是欠采样的, 并且所有成像系统的退化点扩展函数都无法准确获得, 将稀疏表示信号利用图像的超分辨重构(Super resolution image reconstruction, SRIR)技术可以将低分辨率图像重建成远大于探测器分辨率的超分辨率图像^{[9, 10, 11, 12, 13]}, 该过程如图5所示。

	Figure Option View Download New Window
	图5 超分辨图像重建原理Fig.5 Principle of SRIR

图5显示了从有限的观测数据y中恢复原始信号f,通过采用k×n阶观测矩阵R,其中k≪n,k代表观测数据的大小,n代表恢复数据的大小。通过观测图像重建出高分辨率图像需满足以下条件:①观测图像在变换基下具有稀疏性, $\begin{matrix} f = Wθ 中 θ \end{matrix}$ 的绝大部分元素值均为0; ②矩阵 $\begin{matrix} RW \end{matrix}$ 满足RIP条件。

在CS理论下, 图像的超分辨重建需要求解欠定方程组 $\begin{matrix} Y = A^{CS} f, \end{matrix}$ 但由于信号f是稀疏的并且是可压缩的, 这一特征使得欠定方程组可解^[14]。此外, 观测矩阵具有RIP性质也为从 $\begin{matrix} M \end{matrix}$ 个观测值中精确恢复信号提供理论保证, 为了描述CS理论下信号的超分辨重构问题, 首先定义向量 $\begin{matrix} f = {f_{1}, f_{2}, \dots, f_{n}} 的 p \end{matrix}$ 范数为:

$\begin{matrix} ‖ f ‖_{p} = (\overset{N}{\sum_{i = 1}} | f_{i} |^{p})^{1 / p} (3) \end{matrix}$

当 p=0时得到0-范数问题,于是在信号f稀疏并且可压缩的前提下,求解欠定方程组Y=A^CS f)的问题就转化为最小0-范数问题:

$\begin{matrix} \min ‖ Ψ^{T} f ‖_{0} 满足 A^{CS} f = ΦΨX = Y (4) \end{matrix}$

然而,只有通过计算出f中的所有非零项位置的 $\begin{matrix} C_{N}^{K} \end{matrix}$ 种可能的线性组合, 才能得到最优解。所以, 求解式(4)的计算过程属于NP难问题。只要Φ与Ψ不相关,求解l₁优化问题会产生一个同等的解, 从而使NP难问题变成了一个凸优化问题, 并可以化简为线性规划问题^[15]。

3.2 图像重构算法设计

求解式(4)通常采用合并一个正则项即通过罚函数思想求解非线性优化问题, 目标函数表达式如下:

$\begin{matrix} \arg mi n_{x} \frac{1}{2} ‖ y - Ax ‖_{2}^{2} + τ ‖ x ‖_{1} (5) \end{matrix}$

式中: A=R×W是M×N阶矩阵;y为观测向量;x为未知向量;τ>0为正则化参数。

令 $\begin{matrix} x = u - v, \end{matrix}$ 将式(5)转化为带约束的二次规划问题:

$\begin{matrix} \arg \min_{u, v} \frac{1}{2} ‖ y - A (u - v) ‖_{2}^{2} + τ {I^{T}}_{n} u + τ {I^{T}}_{n} v (6) \end{matrix}$

式中: $\begin{matrix} u \geq 0; v \geq 0; I_{n} 为 n \end{matrix}$ 维单位向量。

式(6)可以进一步转化为标准的带约束的二次规划模型:

$\begin{matrix} \{\begin{matrix} \min C^{T} X + \frac{1}{2} X^{T} BX \equiv f (X) \\ s . t . X \geq 0 \end{matrix} (7) \end{matrix}$

式中: $\begin{matrix} X 、 C 和 B \end{matrix}$ 的表达式分别为:

$\begin{matrix} \begin{matrix} X & = [\begin{matrix} u \\ v \end{matrix}]; C = τ I_{2 n} + [\begin{matrix} - A^{T} y \\ A^{T} y \end{matrix}]; \\ B & = [\begin{matrix} A^{T} A & - A^{T} A \\ - A^{T} A & A^{T} A \end{matrix}] \end{matrix} \end{matrix}$

针对上述带约束的二次规划模型, 为了同时满足成像系统在工程应用时快速、有效、精确性高的要求, 需平衡重构效率与质量要求的关系, 本文采用梯度投影稀疏重构(Gradient projection for sparse reconstruction, GPSR)算法求解目标函数。

GPSR算法属于凸优化方法, 该算法于2007年由Figueiredo等^[16]提出, 算法主要思想是当迭代点在可行域内部时, 取该点处的负梯度方向为可行下降方向。当迭代点在可行域边界上时, 取该点处负梯度方向在可行域边界上的投影形成一个可行下降方向。在每次迭代时, 沿着负梯度的方向进行寻优搜索, 从而寻找到目标函数的最小值, 解出新的可行点, 逐步迭代直到寻找到全局最优解。

GPSR算法计算步骤如下:

Step1 参数初始化。给定初始点 $\begin{matrix} x_{0} \in Ω, 0 < a_{\min} < a_{\max}, a_{0} \in [a_{\min}, a_{\max}], 计数器 k = 0, 定义 P (X) 为 X 到可行域 Ω 上的投影, 令 g (x) = \nabla f (x) 。 \end{matrix}$

Step2 梯度投影。如果 $\begin{matrix} x_{k} \end{matrix}$ 满足终止条件, 则结束; 否则按下式计算搜索方向:

$\begin{matrix} d_{k} = P (x_{k} - a_{k} \nabla f (x_{k})) - x_{k} 。 \end{matrix}$

Step3 线搜索。计算新的点x_k+1=x_k+λd_k,其中,λ_k∈(0,1]。

Step4 终止测试或更新。如果||x_k+1-P(x_k-a_k ∇f(x_k))||=0,则算法终止;否则,计算a_k∈[a_min,a_max], $\begin{matrix} ‖ x_{k} - P (x_{k} - a_{k} \nabla f (x_{k})) ‖ = 0_{}_{}_{}, \end{matrix}$ 则算法终止;否则,计算a_k+1∈[a_min,a_max]同时令k=k+1返回到Step2。

3.3 图像重构加速算法

GPSR算法计算效率主要由 $\begin{matrix} a_{k} 的选取和由线搜索计算得到的 a_{k} \end{matrix}$ 能否加速目标函数收敛速度两个因素决定, 为此本文将两点步长梯度法(Barzilai-Borwein, BB)与非单调线搜索策略结合起来应用于传统的梯度投影稀疏重构算法中。

3.3.1 两点步长梯度法

两点步长梯度法是求解式(4)无约束优化问题非常有效的方法^[17], 对于 $\begin{matrix} a_{k} \end{matrix}$ 的选择策略本文借鉴了BB法, 该算法的主要思想是相对简化的拟牛顿法:

Step1 令 $\begin{matrix} d_{k} = - D_{k}^{- 1} g_{k}, 其中 D_{k} \end{matrix}$ 为Hesses矩阵的二阶导数∇² f(x_k)的近似值,gk为式(7)第k步梯度。

Step2 令 $\begin{matrix} D_{k} = a_{k}^{- 1} I, \end{matrix}$ 其中I为单位矩阵, 则BB梯度步长法中的 d_k=-a_k×g_k,从而将迭代公式转化为:x_k+1=x_k-λ_ka_k g_k 。所以在迭代点x_k+1所以在迭代点x_(k+1)处二次近似模型为:

$\begin{matrix} D_{k + 1} λ_{k} d_{k} = \nabla f (x_{k + 1}) - \nabla f (x_{k}) (8) \end{matrix}$

令 $\begin{matrix} a_{k + 1}^{- 1} {^{}}_{}_{} {^{}}_{}_{} \end{matrix}$ s_k=y_k,Step3 利用最小二乘法得出 $\begin{matrix} \min ‖ a_{k + 1}^{- 1} s_{k} - y_{k} ‖_{2}^{2} \end{matrix}$ 值为: $\begin{matrix} a_{k + 1}^{- 1} = {s^{T}}_{K} y_{k} / {s^{T}}_{K} s_{k}, \end{matrix}$ 则:

$\begin{matrix} a_{k + 1} = {s^{T}}_{K} s_{k} / {s^{T}}_{K} y_{k} (9) \end{matrix}$

3.3.2 非单调线搜索策略

由于BB法的目标函数具有非单调性, 通过引入自适应非单调线搜索策略, 可保证GPSR-BB的全局收敛和计算效率^[18], 计算过程如下:

Step1 令 $\begin{matrix} x_{k + 1} = x_{k} + a_{k} d_{k}, 且 a_{k} \end{matrix}$ 满足:

$\begin{matrix} \{\begin{matrix} f (x_{k + 1}) \leq C_{k} + δ a_{k} \nabla f (x_{k}) d_{k} \\ \nabla f (x_{k + 1}) d_{k} \geq σ \nabla f (x_{k}) d_{k} \end{matrix} (10) \end{matrix}$

式中: $\begin{matrix} C_{0} = f (x_{0}), C_{k} 是函数值 f (x_{0}), f (x_{1}), \dots, f (x_{k}) 的凸组合, 0 \leq δ \leq σ \leq 1 。 \end{matrix}$

Step2 在式(10)中加入权重系数并得到改进的自适应线搜索条件, 如式(11)所示:

$\begin{matrix} ω_{k} = \{\begin{matrix} {|\frac{1 + |\min (f_{k - 1}, f_{k})|}{1 + |\max (f_{k - 1}, f_{k})|}|}^{δ}, k < 0 \\ 0, k = 0 \end{matrix} (11) \end{matrix}$

Step3 得到新的非单调线搜索条件为:

$\begin{matrix} f (x_{k + 1}) \leq ω_{k} f (x_{k}) + (1 - ω_{k}) f_{\max} ε < \nabla f (x_{k}), d_{k} > (12) \end{matrix}$

式中: $\begin{matrix} f_{\max} \end{matrix}$ 计算公式为:

$\begin{matrix} f_{\max} = \max \{f (x_{k - i + 1}) | 1 \leq i \leq \min {k + 1, N}\} \end{matrix}$

在式(12)中, 当 $\begin{matrix} ω_{k} \end{matrix}$ 趋近于0时, 搜索条件侧重于非单调策略; 当 $\begin{matrix} ω_{k} \end{matrix}$ 趋近于1时, 搜索条件侧重于单调策略。其中, 分子和分母加1的目的是为了确保分母值不为0。

3.3.3 加速算法计算步骤

基于BB法与自适应非单调线搜索策略相结合的梯度投影并行加速算法(IGPSR-BB)过程如下:

Step1 参数初始化。

给定初始点 $\begin{matrix} x_{0} \in Ω, 0 < a_{\min} < a_{\max}, a_{0} \in [a_{\min}, a_{\max}], 计数器 k = 0, 定义 P (X) 为 X 到可行域 Ω 上的投影, 令 g (x) = \nabla f (x) 。 \end{matrix}$

Step2 梯度投影。并行计算搜索方向: $\begin{matrix} d_{k} = P (x_{k} - a_{k} \nabla f (x_{k})) - x_{k} 。 \end{matrix}$

Step3 非单调线搜索。

(1)令 $\begin{matrix} x^{*} = x_{k} + λ d_{k}, λ = 1 。 \end{matrix}$

(2)如果满足式(12)的约束条件, 则: $\begin{matrix} x_{k + 1} = x^{*}, λ_{k} = λ, s_{k} = x_{k + 1} - x_{k}, y_{k} = \nabla f (x_{k + 1}) - \nabla f (x_{k}), \end{matrix}$ 转到Step4。

(3)否则, 令 $\begin{matrix} λ = 0.5 λ, \end{matrix}$ 转到步骤(1)。

Step4 修正 $\begin{matrix} a_{k} 。 \end{matrix}$

(1)计算 $\begin{matrix} b_{k} = < s_{k}, y_{k} > 。 \end{matrix}$

(2)如果 $\begin{matrix} b_{k} \leq 0, 则 a_{k + 1} = a_{\max} 。 \end{matrix}$

(3)否则, 令 $\begin{matrix} a_{k + 1} \end{matrix}$ 的值表述如下:

$\begin{matrix} a_{k + 1} = \min {a_{\max}, \max {a_{\min}, < s_{k}, s_{k} > / b_{k}}} 。 \end{matrix}$

Step5 终止测试或更新。

(1)如果 $\begin{matrix} ‖ x_{k} - P (x_{k} - a_{k} \nabla f (x_{k})) ‖ = 0, \end{matrix}$ 则算法终止。

(2)否则, 令 k=k+1,返回到Step2。

IGPSR-BB优于GPSR算法的原因是引入BB步长梯度法并对目标函数能够进行自适应的非单调线性调整, 从而能够加快目标函数寻优速度, 提高算法的收敛效率, 并最终加快信号重构速度。

4 实验结果及分析

4.1 实验测试环境

实验测试采用的操作系统为Windows 7旗舰版64位SP1; 处理器为Intel Core i7-4790K 4.00 GHz四核; 内存为16 GB(DDR3 1333 MHz); 显卡为NVIDIA GeForce GTX 980(4095 MB/华硕); 开发工具为Visual Studio 2010, 程序设计语言为C++。

4.2 实验测试方案及结果

为了对IGPSR-BB算法的性能进行验证, 随机选取实拍红外图像样本集进行超分辨实验测试, 并与GPSR、GPSR-BB算法进行比较。

(1)编码孔径成像

首先, 从红外成像系统实拍的500张图像中随机选取20幅图像并将尺度放大3倍组成测试样本集。然后, 从20幅图像中选取2幅场景相对复杂的代表性图像作为超分辨重建效果示例, 如图6所示。最后, 利用图4所示的编码孔径图案, 采用基于傅里叶变换的频谱面编码孔径成像方法对图6所示图像进行编码孔径成像, 获取成像结果如图7所示。

	Figure Option View Download New Window
	图6 超分辨图像重建测试样本Fig.6 Test samples of SRIR

	Figure Option View Download New Window
	图7 编码孔径成像结果Fig.7 Result of coded aperture imaging

(2)信号稀疏表示

信号稀疏表示目的是为了提高信号的非线性函数的逼近能力, 利用光学系统成像的分片光滑性, 实现了信号在傅里叶变换域的稀疏表示并生成观测矩阵, 编码孔径成像稀疏表示结果如图8所示。

	Figure Option View Download New Window
	图8 编码孔径成像傅里叶变换Fig.8 Fourier transform of coded aperture imaging

(3)图像的超分辨重建

首先, 采用IGPSR-BB算法对稀疏的图像信号进行超分辨重建。其中, 初始化参数 $\begin{matrix} a_{\min} = 10^{- 30}, a_{\max} = 10^{30} 。 \end{matrix}$ 超分辨重建后的结果如图9所示。然后, 利用IGPSR-BB算法对测试样本集中的20幅图像进行超分辨重建, 分别计算重建算法的迭代次数、计算时间、峰值信噪比(PSNR)和结构相似度(SSIM), 计算结果取平均值。最后, 在相同的实验环境下, 与GPSR和GPSR-BB算法进行了对比, 结果如表1所示。

	Figure Option View Download New Window
	图9 超分辨图像重建结果Fig.9 Results of SRIP

表1 图像信号重建数据对比 Table 1 Data comparison of SRIR

通过表1数据对比结果可知, IGPSR-BB算法在迭代次数方面明显优于GPSR和GPSR-BB算法, 从而极大地提高了计算效率, 节省了图像重建的时间。而且PSNR和SSIM值优于传统方法, 可以满足工程应用技术指标的要求。

5 结束语

通过频谱面孔径编码器对采样信号进行编码压缩, 再利用傅里叶变换实现信号的稀疏表示, 提出一种改进的梯度投影稀疏重构并行加速算法完成对欠采样信号的超分辨重建。实验结果表明:本文算法能够提高图像的峰值信噪比和结构相似度, 同时达到去噪的目的, 并表现出较好的实时性, 具有一定的工程应用价值。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. [本文引用:1]
[2]	焦李成, 杨淑媛, 刘芳, 等. 压缩感知回顾与展望[J]. 电子学报, 2011, 39(7): 1651-1662. Jiao Li-cheng, Yang Shu-yuan, Liu Fang, et al. Development and prospect of compressive sensing[J]. Acta Electronica Sinica, 2011, 39(7): 1651-1662. [本文引用:1]
[3]	王忠良, 冯燕, 肖华, 等. 高光谱图像的分布式压缩感知成像与重构[J]. 光学精密工程, 2015, 23(4): 1131-1137. Wang Zhong-liang, Feng Yan, et al. Xiao Hua. Distributed compressive sensing imaging and reconstruction of hyperspectral imagery[J]. Optics and Precision Engineering, 2015, 23(4): 1131-1137. [本文引用:1]
[4]	周渝人, 耿爱辉, 张强, 等. 基于压缩感知的红外与可见光图像融合[J]. 光学精密工程, 2015, 23(3): 855-863. Zhou Yu-ren, Geng Ai-hui, Zhang Qiang, et al. Fusion of infrared and visible images based on compressive sensing[J]. Optics and Precision Engineering, 2015, 23(3): 855-863. [本文引用:1]
[5]	Dharmpal T, Jason N L, Michael B W, et al. A new compressive imaging camera architecture using optical-domain compression[J]. SPIE-IS&T, 2006, 6065: 606509-1-10 [本文引用:1]
[6]	严奉霞, 王泽龙, 朱炬波, 等. 压缩感知理论与光学压缩成像系统[J]. 国防科技大学学报, 2014, 36(2): 140-147. Yan Feng-xia, Wang Ze-long, Zhu Ju-bo, et al. Compressive sensing theory and optical compressive imaging systems[J]. Journal of National University of Defense Technology, 2014, 36(2): 140-147. [本文引用:1]
[7]	李珅, 马彩文, 李艳, 等. 压缩感知重构算法综述[J]. 红外与激光工程, 2013, 42(增刊1): 225-232. Li Kun, Ma Cai-wen, Li Yan, et al. Survey on reconstruction algorithm based on compressive sensing[J]. Infrared and Laser Engineering, 2013, 42(Sup. 1): 225-232. [本文引用:1]
[8]	Willett R M, Marcia R F, Nichols J M. Compressed sensing for practical optical imaging systems: a tutorial[J]. Optical Engineering, 2011, 50(7): 072601-1-11. [本文引用:1]
[9]	王春哲, 李杰, 李明晶, 等. 一种多扭曲失真图像的质量评价方法[J]. 液晶与显示, 2015, 30(04): 681-686. Wang Chun-zhe, Li Jie, Li Ming-jing, et al. Image quality assessment algorithm for multi-distorted image[J]. Chinese Journal of Liquid Crystals and Displays , 2015, 30(4): 681-686. [本文引用:1]
[10]	曹雷, 陈洪斌, 邱琪, 等. 盲图像复原研究现状[J]. 中国光学, 2014, 7(1): 68-78. Cao Lei, Chen Hong-bin, Qiu Qi, et al. Research status of blind image restoration[J]. Chinese Optics, 2014, 7(1): 68-78. [本文引用:1]
[11]	柯洪昌, 孙宏彬. 图像序列的显著性目标区域检测方法[J]. 中国光学, 2015, 8(5): 768-774. Ke Hong-chang, Sun Hong-bin. A saliency target area detection method of image sequence[J]. Chinese Optics, 2015, 8(5): 768-774. [本文引用:1]
[12]	张振东, 陈健, 王伟国, 等. 基于SSIM_NCCDFT的超分辨率复原评价方法研究[J]. 液晶与显示, 2015, 30(4): 713-721. Zhang Zhen-dong, Chen Jian, Wang Wei-guo, et al. Evaluation method of super-resolution restoration based on SSIM_NCCDFT[J]. Chinese Journal of Liquid Crystals and Displays, 2015, 30(4): 713-721. [本文引用:1]
[13]	Yang J, Wright J, Huang T S, et al. Image super-resolution via sparse representation[J]. IEEE Transaction on Image Processing, 2010, 19(11): 2861-2873. [本文引用:1]
[14]	邓承志, 田伟, 汪胜前, 等. 近似稀疏正则化的红外图像超分辨率重建[J]. 光学精密工程, 2014, 22(6): 1648-1654. Deng Cheng-zhi, Tian Wei, Wang Sheng-qian, et al. Super-resolution reconstruction of approximate sparsity regularized infrared images[J]. Optics and Precision Engineering, 2014, 22(6): 1648-1654. [本文引用:1]
[15]	王军华, 黄知涛, 周一宇, 等. 基于近似l0的稳健稀疏重构算法[J]. 电子学报, 2012, 40(6): 1185-1189. Wang Jun-hua, Huang Zhi-tao, Zhou Yi-yu, et al. Robust saprse reconvery based on approximate l0 Norm[J]. Acta Electronica Sinica, 2012, 40(6): 1185-1189. [本文引用:1]
[16]	Figueiredo M A T, Nowak R D, Wright S J. Gradient projection for sparse reconstruction: application to compressed sensing and other inverse problems[J]. IEEE Journal of Selected Topics in Signal Processing, 2007, 1(4): 586-597. [本文引用:1]
[17]	Dai Y H, Zhang H. Adaptive two-point stepsize gradient algorithm[J]. Numerical Algorithms, 2001, 27(4): 377-385. [本文引用:1]
[18]	Hu Sheng-long, Huang Zheng-hai, Lu Nan. A non-monotone line search algorithm for unconstrained optimization[J]. Journal of Scientific Computer, 2010, 42(1): 38-53. [本文引用:1]

2006

0.0

... 压缩感知(Compressed sensing,CS)理论的提出突破了传统奈奎斯特采样定理的限制^[1],使得通过低分辨率探测器获取高分辨率图像信息成为可能 ...

2011

0.0

. 2011, 39(7):1651-1662

Development and prospect of compressive sensing

压缩感知回顾与展望

Jiao Li-cheng , Yang Shu-yuan , Liu Fang

焦李成, 杨淑媛, 刘芳

Compressive Sensing(CS) is a new developed theoretical framework for information acquisition and processing,which is based on matrix analysis,statistical probability theory,topological geometry,optimization and opsearch,functional analysis and so on.The high-dimensional signals can be recovered from the low-dimensional and sub-Nyquist sampling data based on the compressibility of signals.It not only inspires us to survey the linear problem again,but also enriches the optimization approaches for signal recovery to promote the combination of mathematics with engineering application.Nowadays the researches on compressive sensing have developed from the earlier concept understanding,numerical simulation,principle verification,and primary system designation,to the deeper researches on theory,development and application of practical system.In this paper,we introduce the basic idea of compressive sensing,and the development history,current and future challenges.

压缩感知是建立在矩阵分析、统计概率论、拓扑几何、优化与运筹学、泛函分析等基础上的一种全新的信息获取与处理的理论框架.它基于信号的可压缩性,通过低维空间、低分辨率、欠Nyquist采样数据的非相关观测来实现高维信号的感知.压缩感知不仅让我们重新审视线性问题,而且丰富了关于信号恢复的优化策略,极大的促进了数学理论和工程应用的结合.目前,压缩感知的研究正从早期的概念理解、数值仿真、原理验证、系统初步设计等阶段,转入到理论的进一步深化,以及实际系统的开发与应用阶段.本文分析了压缩感知的原理与应用,综述了压缩感知的最新进展及存在的问题,指出了进一步研究的方向.

... 近些年,CS理论在压缩成像、医疗成像和雷达成像等领域得到了广泛的应用^[2,3,4],比较有代表性的成果是美国Rice大学研制的单像素相机^[5],此外文献[6]详细阐述了光学压缩成像系统研究进展,并对今后面临的挑战性问题进行了探讨 ...

2015

0.0

. 2015, 23(4):1131-1137 DOI:doi:10.3788/OPE.20152304.1131

Distributed compressive sensing imaging and reconstruction of hyperspectral imagery

高光谱图像的分布式压缩感知成像与重构

Wang Zhong-liang , Feng Yan

王忠良, 冯燕, 肖华

根据高光谱数据的特点,提出了一种基于像元的分布式压缩采样模型来实现高光谱图像的有效压缩采样与重构。搭建了能实现该模型的压缩采样光谱成像系统,并研究了用于该系统成像的重构算法。在图像采集阶段,将高光谱数据分为参考像元和压缩感知像元;地面像元的辐射能通过棱镜进行谱带分离,再利用数字微镜器件实现谱带的线性编码。对压缩感知像元进行低采样率的线性编码,对参考像元进行采样率为1的线性编码。压缩采样数据重构时,不再采用传统方法直接重构高光谱数据,而是利用线性混合模型将重构高光谱数据转换成端元提取和丰度估计,然后根据重构的端元和丰度恢复原数据。对比实验表明,在压缩采样数据为总数据的20%时,重构的平均信噪比提高了10dB。所设计的成像系统应用压缩感知理论减少了采集的数据量,采样方式简单,可应用于星载或机载的高光谱压缩感知成像。

2015

0.0

2006

0.0

2014

0.0

2013

0.0

. 2013, 42(增刊1):225-232 DOI:doi:10.3969/j.issn.1007-2276.2013.z1.043

Survey on reconstruction algorithm based on compressive sensing

压缩感知重构算法综述

Li Kun , Ma Cai-wen , Li Yan

李珅, 马彩文, 李艳

现代社会信息量的激增带来了信号采样、传输和存储的巨大压力,而近年来出现的压缩感知理论(Compressed Sensing,CS)为解决该问题提供了契机.该理论指出:对于稀疏或可压缩的信号,能够以远低于奈奎斯特频率对其进行采样,并通过设计重构算法来精确的恢复该信号.介绍了压缩感知理论的基本框架并讨论了该理论关于信号压缩的采样过程;综述了压缩感知理论的重构算法,其中着重介绍了最优化算法和贪婪算法并比较了各种算法之间的优劣,最后探讨了压缩感知理论重构算法未来的研究重点.通过对压缩感知理论重构算法较为系统的介绍和比较,为压缩感知重构算法的改进和应用提供了理论依据.

... 压缩传感理论涉及以下几个方面^[7]: ...

2011

0.0

... 1 编码孔径成像原理Willett等^[8]提出了基于CS理论的采用频谱编码的方法,利用大于探测器分辨率的相位板对图像傅里叶频谱进行编码,探测器记录编码后的图像信息,通过重构算法可以恢复得到一个与相位板分辨率一样的红外图像 ...

2015

0.0

. 2015, 30(04):681-686 DOI:doi:10.3788/YJYXS20153004.0681

Image quality assessment algorithm for multi-distorted image

一种多扭曲失真图像的质量评价方法

Wang Chun-zhe , Li Jie , Li Ming-jing

王春哲, 李杰, 李明晶

针对现有评价方法不适合于多扭曲失真图像这一问题,本文展开了对多扭曲失真图像评价方法的研究.在分析图像的边缘信息和奇异值向量对视觉特征的表征能力的基础上,提出一种基于边缘信息奇异值分解的图像质量评价算法.首先,利用Sobel算子提取参考图像及失真图像视觉敏感的边缘信息,再对两图像的边缘信息进行奇异值分解,利用奇异值向量之间的夹角来描述失真图像的畸变程度.最后,采用LIVE数据库中的450张多扭曲的失真图像验证该文算法,并与MSE、PSNR、SSIM、CSSIM等算法进行了对比.实验结果表明,该文算法对多扭曲失真图像的质量评价具有更高的稳定性,主客观评价的一致性较传统评价方法更好.通过对比时间效率,该方法基本上满足实际需求,具有更高的适用性.

... 1 图像重建问题描述由于经过编码孔径成像系统所生成的数字信号是欠采样的,并且所有成像系统的退化点扩展函数都无法准确获得,将稀疏表示信号利用图像的超分辨重构(Super resolution image reconstruction,SRIR)技术可以将低分辨率图像重建成远大于探测器分辨率的超分辨率图像^{[9,10,11,12,13]},该过程如图5所示 ...

2014

0.0

. 2014, 7(1):68-78 DOI:doi:10.3788/CO.20140701.0068

Research status of blind image restoration

盲图像复原研究现状

Cao Lei , Chen Hong-bin , Qiu Qi

曹雷, 陈洪斌, 邱琪

Blind image restoration is an approach to estimate both the original image and the point spread function from degraded images, when there is no or little knowledge of the point spread function of the degraded process. In this paper, the main algorithms of blind image restoration are reviewed and classified into four types, according to their theory origins and relationships, and analysis is made for all the types of blind image restoration algorithms and relevant improved algorithms. This will be helpful to better understand the theory of blind image restoration and to restore degraded images.

盲图像复原是在未知或不完全确知相关原始图像与成像点扩展函数的先验知识的情形下，利用所观测到的降质图像对原始图像和点扩展函数进行估计的一种图像处理方法。本文对近年来涌现出的主要盲图像复原算法进行了回顾，并根据相应的理论来源及相互联系将其划分为四大类，对各类复原算法及其改进算法进行了分析和讨论，为更清晰与深刻地认识和理解盲图像复原理论、解决实际图像降质问题提供参考。

2015

0.0

. 2015, 8(5):768-774 DOI:doi:10.3788/CO.20150805.0768

A saliency target area detection method of image sequence

图像序列的显著性目标区域检测方法

Ke Hong-chang , Sun Hong-bin.

柯洪昌, 孙宏彬

摘　要：针对传统视觉显著性模型在自顶向下的任务指导和动态信息处理方面的不足,设计并实现了融入运动特征的视觉显著性模型。利用该模型提取了图像的静态特征和动态特征,静态特征的提取在图像的亮度、颜色和方向通道进行,运动特征的提取采用基于多尺度差分的特征提取方法实现,然后各通道分别通过滤波、差分得到显著图,在生成全局显著图时,提出多通道参数估计方法,计算图像感兴趣区域与眼动感兴趣区域的相似度,从而可在图像上准确定位目标位置。针对20组视频图像序列（每组50帧）进行了实验,结果表明：本文算法提取注意焦点即目标区域的平均相似度为0.87,使用本文算法能够根据不同任务情境,选择各特征通道的权重参数,从而可有效提高目标搜索的效率。

2015

0.0

. 2015, 30(4):713-721 DOI:doi:10.3788/YJYXS20153004.0713

Evaluation method of super-resolution restoration based on SSIM_NCCDFT

基于SSIM_NCCDFT的超分辨率复原评价方法研究

Zhang Zhen-dong , Chen Jian , Wang Wei-guo

张振东, 陈健, 王伟国

传统的图像质量评价方法很多,但是并非针对超分辨率复原算法的特定评价指标.一种超分辨率复原算法复原性能的好坏,至今没有一个统一的评价标准,这使得超分辨率复原算法的发展受到很大限制.针对传统的超分辨率复原评价体系只关注图像某一方面统计特性的问题,提出一种基于SSIM_NCCDFT的超分辨率复原评价方法.该评价方法结合了空间域的灰度均值、对比度以及频域自相关,能够同时评价超分辨率复原结果在空间域的复原效果和对频率域信息的复原精度.实验结果表明:SSIM_NCCDFT可以准确反映图像退化的程度. 相对于PSNR,SSIM_NCCDFT的优势是其同时反映了频域和空域复原的精度,评价更加全面.本文提出的基于SSIM_NCCDFT的超分辨率复原评价方法同时考虑了超分辨率复原中频率域和空间域的复原性能,评价结果较为全面,能够有效地评价复原图像中的噪声和模糊等现象,对超分辨率复原方法的评价具有一定的指导意义.

2010

0.0

2014

0.0

. 2014, 22(6):1648-1654 DOI:doi:10.3788/OPE.20142206.1648

Super-resolution reconstruction of approximate sparsity regularized infrared images

近似稀疏正则化的红外图像超分辨率重建

Deng Cheng-zhi , Tian Wei , Wang Sheng-qian

邓承志, 田伟, 汪胜前

摘　要：针对红外图像分辨率低、受噪声影响严重等问题,引入近似稀疏正则化和K-奇异值分解（K-SVD）法,提出了基于近似稀疏表示模型的红外图像超分辨率重建方法.考虑到红外图像受到噪声污染,首先建立了稳健近似稀疏表示模型.针对已有字典训练方法时间消耗巨大问题,在假定低分辨率图像空间和高分辨率图像空间具有相似流形的前提下,联合近似稀疏表示模型和K SVD方法,提出近似稀疏约束的基于K-SVD的高低分辨率字典对学习算法.最后,通过高分辨字典和对应的红外图像群稀疏表示系数重建得到高分辨率的红外图像.为了验证算法的性能,对提出的算法与稀疏性正则化的图像超分辨模型（SRSR）和Zeyde算法进行了实验比较.结果表明,本文方法能够较好地减少红外图像中的噪声,同时获得更好的超分辨率重建效果.

... 在CS理论下,图像的超分辨重建需要求解欠定方程组 Y=ACSf,但由于信号f是稀疏的并且是可压缩的,这一特征使得欠定方程组可解^[14] ...

2012

0.0

. 2012, 40(6):1185-1189 DOI:doi:10.3969/j.issn.0372-2112.2012.06.020

Robust saprse reconvery based on approximate l0 Norm

基于近似l0的稳健稀疏重构算法

Wang Jun-hua , Huang Zhi-tao , Zhou Yi-yu

王军华, 黄知涛, 周一宇

摘　要：针对测量值受噪声污染的稀疏重构问题,本文提出了稳健近似l0范数最小化算法.该算法首先利用反正切函数近似l0范数,然后建立基于近似l0范数的含噪稀疏重构模型,最后通过拟牛顿法求解该模型,并分析了算法的收敛性.数值仿真表明,本文提出的算法重构稀疏向量时需要较少的测量值,且具有较高的计算精度.

... 只要 Φ与 Ψ不相关,求解l1优化问题会产生一个同等的解,从而使NP难问题变成了一个凸优化问题,并可以化简为线性规划问题^[15] ...

2007

0.0

... GPSR算法属于凸优化方法,该算法于2007年由Figueiredo等^[16]提出,算法主要思想是当迭代点在可行域内部时,取该点处的负梯度方向为可行下降方向 ...

2001

0.0

... 两点步长梯度法是求解式(4)无约束优化问题非常有效的方法^[17],对于 ak的选择策略本文借鉴了BB法,该算法的主要思想是相对简化的拟牛顿法: ...

2010

0.0

... 由于BB法的目标函数具有非单调性,通过引入自适应非单调线搜索策略,可保证GPSR-BB的全局收敛和计算效率^[18],计算过程如下: ...