改进的离散混合蛙跳算法压缩感知信号重构及应用

引用本文

刘洲洲, 王福豹. 改进的离散混合蛙跳算法压缩感知信号重构及应用.吉林大学学报:工学版, 2016, 46(4): 1261-1268
LIU Zhou-zhou, WANG Fu-bao. Improvement of discrete shuffled frog-leaping algorithm and application in compressed sensing reconstruction. Journal of Jilin University Engineering and Technology Edition, 2016, 46(4): 1261-1268 复制到剪切板

Permissions

改进的离散混合蛙跳算法压缩感知信号重构及应用

刘洲洲^1,², 王福豹²

1.西安航空学院电子工程学院,西安 710077

2.西北工业大学电子信息学院,西安 710072

作者简介:刘洲洲(1981-),男,博士研究生.研究方向:无线传感器网络.E-mail:nazi2005@126.com

基金:国家自然科学基金项目(61103242, 61401499); 陕西省教育厅科研计划项目(16JK1395)

摘要

针对工程离散优化问题特点,定义了具有普遍意义的青蛙编码方式,设计了编码位调换更新机制,提出了自适应权重因子和双模子族群策略。在此基础上,将改进的离散混合蛙跳算法(Discrete shuffled frog leaping algorithm,DSFLA)应用于压缩感知重构算法中,将未知重构信号理解为青蛙编码方式,利用DSFLA算法全局寻优能力得到次最优信号重构信息,从而实现了稀疏度未知情况下的信号重构。最后对典型TSP(Travelling salesman problem)问题算例和WSNs多目标定位问题进行仿真,仿真结果表明:改进的DSFLA具有更强的复杂问题求解能力,基于改进DSFLA压缩感知重构算法的WSNs目标定位精度优于传统信号重构算法,且抗噪能力达到25~45 dB。

关键词: 计算机应用; 无线传感器网络; 离散混合蛙跳算法; 压缩感知重构算法; 多目标定位

中图分类号:TP393 文献标志码:A 文章编号:1671-5497(2016)04-1261-08

Improvement of discrete shuffled frog-leaping algorithm and application in compressed sensing reconstruction

LIU Zhou-zhou^1,², WANG Fu-bao²

1.School of Electrical Engineering,Xi'an Aeronautical University, Xi'an 710077, China

2.School of Electronics and Information, Northwestern Polytechnical University,Xi'an 710072, China

Abstract

An improvement of Discrete Shuffled Frog-leaping Algorithm (DSFLA) is proposed. Fist, according to the characteristics of discrete optimization problems, the frog coding of universal significance is defined, which is important for DSFLA in solving discrete optimization effectively. Then, the update mechanism based on “swapping of coded bits” for DSFLA is designed, and an adaptive weighting factor and sub-ethic dual strategy are presented. Finally, the improved DSFLA is applied in compressed sensing reconstruction algorithm, in which the unknown reconstructed signal encoding is taken as the frog code. Typical TSP problems and multiple target localization in WSN are simulated. Simulation results show that the improved DSFLA has prominent ability to solve complex problems, and the perception accuracy of WSNs target reconstruction based on improved DSFLA CS reconstruction algorithm is better than that of the traditional signal reconstruction algorithm, and the anti noise capacity reaches 25~45 dB.

Keyword: computer application; wireless sensor networks; discrete shuffle frog leaping algorithm; compressed sensing reconstruction algorithm; multiple target localization

Show Figures

0 引言

由于工程实际问题通常具有大规模、非线性、建模困难等特点, 传统的优化算法在求解精度、求解效率等方面已不能有效解决, 因此寻求适用于大规模并行计算的智能优化方法成为当前研究热点之一^[1]。2003年, 学者Eusuff和Lansey^[2]通过模拟青蛙群体觅食行为, 提出了一种新的启发式智能计算技术— — 混合蛙跳算法(Shuffled frog leaping algorithm, SFLA), 算法按照子种群划分思想更新青蛙模因信息, 实现了局部搜索与全局信息交换有机结合, 具有较强的鲁棒性^[3]。目前, 关于混合蛙跳算法的研究主要集中于算法改进和在连续优化问题中的应用等方面^{[4, 5]}, 关于离散混合蛙跳算法的研究则相对较少, 且缺乏相对系统的理论研究, 因此, 开展离散混合蛙跳算法研究具有重要意义。

压缩感知(Compressed sensing, CS)^[6]是一种新型的数据压缩和重构理论, 具有编码简单、抗误码性好、能够实现高效的压缩等特点^[7], 为无线传感器网络(WSNs)、图像处理、目标跟踪等领域提供了全新的解决问题的思路^{[8, 9, 10]}。信号重构算法是压缩感知理论关键技术之一, 学者们相继提出了正交匹配追踪(OMP)算法、贪婪匹配跟踪(GMP)算法、正则化正交匹配追踪(ROMP)算法等。文献[7]提出了基于自适应方向提升稀疏表示的重构方法, 有效克服了传统信号重构过程中方向选择性差的局限性。文献[9]将正交基字典引入到信号重构中, 得到了最稀疏的信号表示, 但是算法复杂度相对较高。文献[11]分析了稀疏度 $\begin{matrix} K \end{matrix}$ 未知情况下的信号重构方法, 但是需要跟踪和扩充有效子空间。文献[12]研究了基于萤火虫优化算法的压缩感知重构算法, 并对WSNs多目标定位问题进行了求解, 仿真结果证明了该方法的有效性。

本文主要针对离散混合蛙跳算法及其在压缩感知重构算法中的应用进行研究。首先在对离散优化问题特点分析的基础上, 定义具有普遍意义的青蛙编码方式, 给出编码位调换青蛙更新机制, 并提出自适应权重因子和双模子族群策略。其次设计基于改进DSFLA的压缩感知重构算法(IDSFLA), 将未知重构信号理解为青蛙编码方式, 利用DSFLA算法全局寻优能力得到次最优信号重构信息。最后采用典型TSP算例和WSNs多目标定位问题进行仿真, 验证改进DSFLA算法和基于改进DSFLA压缩感知重构算法的性能。

1 离散混合蛙跳算法及其改进

1.1 DSFLA青蛙编码

离散优化问题是指决策变量 $\begin{matrix} X = (x_{1}, \dots, x_{k}, \dots, x_{n}) \end{matrix}$ 在正整数范围内变化的优化问题。传统的智能优化算法主要用于连续优化问题的求解, 即决策变量是连续变化的, 如果直接应用于离散优化问题, 会产生大量不符合要求的解, 降低了算法收敛速度, 且优化精度很低。在智能优化算法中, 每个粒子编码代表问题的一个解^{[13, 14]}, 因此, 粒子的编码方式及相应的编码更新机制直接决定了算法能否高效解决离散优化问题。

定义1 离散混合蛙跳算法。对于混合蛙跳算法, 如果决策变量 $\begin{matrix} X = (x_{1}, \dots, x_{k}, \dots, x_{n}) \end{matrix}$ 在正整数范围内变化, 则称其为离散混合蛙跳算法(Discrete shuffled frog leaping algorithm, DSFLA)。

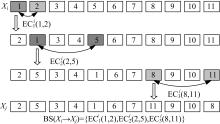
定义2 离散混合蛙跳算法青蛙粒子编码。在DSFLA中, 青蛙粒子 $\begin{matrix} X_{i} \end{matrix}$ 的编码方式定义为 $\begin{matrix} X_{i} = (x_{i 1}, \dots, x_{ik}, \dots, x_{in}), \end{matrix}$ 其中 $\begin{matrix} x_{ik} \in [0, m], \end{matrix}$ 且 $\begin{matrix} Q = n - Z (Q 、 Z 分别为 X_{i} \end{matrix}$ 所有维度不同的自然数数目和所有维度数值为0的个数)。例如, 对于青蛙粒子 $\begin{matrix} F_{a} (1, 2, 0, 3, 4), \end{matrix}$ 其 $\begin{matrix} Q = 4, Z = 1, \end{matrix}$ 即变量维数为5的 $\begin{matrix} F_{a} \end{matrix}$ 共使用了4种不同的自然数, 并且存在1个维度取值为0。

1.2 编码位调换青蛙更新机制

观察定义2, 可以发现, 两个不同的青蛙编码能够通过一系列的编码位调换完成相互转换, 例如, 对于编码 $\begin{matrix} F_{a} = (1, 2, 0, 3, 4, 5) \end{matrix}$ 和编码 $\begin{matrix} F_{b} = (2, 1, 0, 4, 3, 5), \end{matrix}$ 将 $\begin{matrix} F_{a} \end{matrix}$ 中的第1、2个编码位以及第4、5个编码位调换就可以得到编码 $\begin{matrix} F_{b} 。 \end{matrix}$

定义3 编码位调换。对于青蛙 $\begin{matrix} X_{i} \end{matrix}$ , 其编码中第 $\begin{matrix} k 、 l \end{matrix}$ 个编码位调换定义为 $\begin{matrix} E C^{i} (k, l), \end{matrix}$ 其中, $\begin{matrix} k \neq lΛk, l \in {1, \dots, n} 。 \end{matrix}$

定义4 编码位调换集。对于青蛙 $\begin{matrix} X_{i} \end{matrix}$ 和 $\begin{matrix} X_{j}, X_{i} \end{matrix}$ 能够通过一系列编码位调换转化为 $\begin{matrix} X_{j}, \end{matrix}$ 则将该系列编码位调换定义为编码位调换集 $\begin{matrix} BS (X_{i} \to X_{j}) = {E C_{1}^{i}, \dots, E C_{h}^{i}, \dots, E C_{θ}^{i}}, \end{matrix}$ 其中, $\begin{matrix} E C_{h}^{i} \end{matrix}$ 为第 $\begin{matrix} h \end{matrix}$ 个编码位调换, $\begin{matrix} θ \end{matrix}$ 为编码位调换集中编码位调换的个数( $\begin{matrix} 0 \leq θ \leq n - 1 \end{matrix}$ )。图1给出了编码位调换及编码位调换集示意图。

	Figure Option View Download New Window
	图1 编码位调换及编码位调换集示意图Fig.1 Coding bit exchange and coding position exchange diagram

定义5 青蛙更新机制。DSFLA青蛙更新机制定义为:

$\begin{matrix} X_{new} = X_{W} + r 2 ⨀ BS (X_{W} \to X_{B}) (1) \end{matrix}$

式中: $\begin{matrix} r \end{matrix}$ 为权重因子且为随机正整数; $\begin{matrix} X_{W} 、 X_{B} \end{matrix}$ 分别为子族群内适应度最差的解和适应度最优的解, $\begin{matrix} r ⨀ BS (X_{W} \to X_{B}) \end{matrix}$ 表示取 $\begin{matrix} BS (X_{W} \to X_{B}) \end{matrix}$ 前 $\begin{matrix} r \end{matrix}$ 个编码位调换( $\begin{matrix} 0 \leq r \leq θ \end{matrix}$ )。

1.3 改进的离散混合蛙跳算法(IDSFLA)

对于标准混合蛙跳算法, 随着迭代次数的不断增加, 算法进化速度明显降低甚至会停滞, 陷入早熟。相关研究表明^[15]增加青蛙群体多样性和扰动性能够使得算法进一步深度搜索, 提高发现最优解概率, 本文在此基础上提出了自适应权重因子和双模子族群策略。

(1)自适应权重因子。在式(1)的基础上, 改进的离散混合蛙跳算法(IDSFLA)采用的自适应权重因子为:

$\begin{matrix} \begin{matrix} r' = int [n \times ξ_{1} \times r_{\min} \times {(\frac{r_{\max}}{r_{\min}})}^{\frac{1}{1 + c_{3} \times t / T_{\max}}} + \\ n \times ξ_{2} \times rand (0, 1)] (2) \end{matrix} \end{matrix}$

式中: $\begin{matrix} t \end{matrix}$ 为算法迭代次数; $\begin{matrix} T_{\max} \end{matrix}$ 为算法最大迭代次数; $\begin{matrix} ξ_{1} 、 ξ_{2} \in (0, 1) \end{matrix}$ 且为常数; $\begin{matrix} r_{\max} 、 r_{\min} \end{matrix}$ 表示为 $\begin{matrix} r' \end{matrix}$ 的最大值和最小值; $\begin{matrix} n \end{matrix}$ 为青蛙编码维数。

(2)双模子族群策略。双模子族群策略将青蛙子族群划分为改良群和优良群, 在改良群和优良群内, 青蛙分别执行不同的更新策略。

定义6 种群进化控制因子 $\begin{matrix} EC (t) 。 EC (t) \end{matrix}$ 定义为:

$\begin{matrix} EC (t) = |\frac{f [P_{g} (t)] - f [P_{g} (t - 1)]}{α}| (3) \end{matrix}$

式中: $\begin{matrix} f [P_{g} (t)] 、 f [P_{g} (t - 1)] \end{matrix}$ 分别为第 $\begin{matrix} t 、 t - 1 \end{matrix}$ 代种群最优适应度值; $\begin{matrix} α \end{matrix}$ 为调整参数。从式(3)可看出, $\begin{matrix} EC (t) > 0 \end{matrix}$ 表示算法处于进化状态, 且 $\begin{matrix} EC (t) \end{matrix}$ 取值越大, 算法种群样本差异性越大; $\begin{matrix} EC (t) = 0 \end{matrix}$ 表示算法停止进化。

定义7 改良群规模 $\begin{matrix} I_{i, s} (t) 。 \end{matrix}$ 对于子族群 $\begin{matrix} E_{i}, \end{matrix}$ 其改良群规模 $\begin{matrix} I_{i, s} (t) \end{matrix}$ 定义为:

$\begin{matrix} I_{i, s} (t) = round [q \times τ \times (1 - EC (t))] (4) \end{matrix}$

式中: $\begin{matrix} τ \end{matrix}$ 为常数, $\begin{matrix} q \end{matrix}$ 为青蛙子族群规模, 通常设定 $\begin{matrix} I_{\min} \leq I_{i, s} (t) \leq I_{\max} 。 \end{matrix}$

从式(3)(4)可以看出, 算法迭代初期, $\begin{matrix} EC (t) \end{matrix}$ 取值较大, 使得 $\begin{matrix} I_{i, s} (t) \end{matrix}$ 较小; 随着算法迭代次数不断增加, $\begin{matrix} EC (t) \end{matrix}$ 逐渐变小, 算法进化趋于停滞, 同时, $\begin{matrix} I_{i, s} (t) \end{matrix}$ 逐渐变大, 使得算法拥有较多的改良群青蛙个体, 改良群青蛙个体能够在更大的空间进行探索, 提高了算法全局寻优能力。改良群青蛙个体更新策略为:

$\begin{matrix} \begin{matrix} X_{new}^{i} (t + 1) = X_{w}^{i} (t) + r_{1} \times BS (X_{w}^{i} \to P_{B}^{i}) + \\ r_{2} \times BS (X_{w}^{i} \to P_{g}) (5) \\ r_{1} \leq |BS (X_{w}^{i} \to P_{B}^{i})|, r_{2} \leq |BS (X_{w}^{i} \to P_{g})| (6) \end{matrix} \end{matrix}$

式中: $\begin{matrix} X_{w}^{i} (t) \end{matrix}$ 为 $\begin{matrix} E_{i} \end{matrix}$ 改良群中适应度值最差的解; $\begin{matrix} P_{B}^{i} 、 P_{g} \end{matrix}$ 分别为子族群最优解和全局最优解; $\begin{matrix} |BS (X_{w}^{i} \to P_{B}^{i})| \end{matrix}$ 和 $\begin{matrix} |BS (X_{w}^{i} \to P_{g})| \end{matrix}$ 分别为 $\begin{matrix} BS (X_{w}^{i} \to P_{B}^{i}) \end{matrix}$ 和 $\begin{matrix} BS (X_{w}^{i} \to P_{g}) \end{matrix}$ 内编码位调换的个数; $\begin{matrix} r_{1} 、 r_{2} \end{matrix}$ 采用式(2)自适应策略, 且满足式(6)。

如果式(5)产生的新个体适应度值优于原个体, 则替代原个体, 否则随机生成新的个体进行替代。

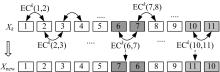
根据式(4), 子族群 $\begin{matrix} E_{i} \end{matrix}$ 的优良群规模 $\begin{matrix} G_{i, s} (t) \end{matrix}$ 为:

$\begin{matrix} G_{i, s} (t) = q - I_{i, s} (t) (7) \end{matrix}$

优良群青蛙个体更新策略为:

$\begin{matrix} \begin{matrix} X_{new}^{i} (t + 1) = X_{k}^{i} (t) + r_{3} \otimes {E C^{k} (1, 2), \\ E C^{k} (2, 3), \dots, E C^{k} (n - 1, n)} (8) \end{matrix} \end{matrix}$

式中: $\begin{matrix} X_{k}^{i} (t) \end{matrix}$ 为 $\begin{matrix} E_{i} \end{matrix}$ 优良群内适应度值最好的解; $\begin{matrix} r_{3} \end{matrix}$ 满足式(2), $\begin{matrix} r_{3} \otimes {E C^{k} (1, 2), E C^{k} (2, 3), \dots, E C^{k} (n - 1, n)} \end{matrix}$ 表示为随机选取 $\begin{matrix} r_{3} \end{matrix}$ 个编码位调换操作, 通常设定 $\begin{matrix} r_{3} \leq R_{\max} (R_{\max} \end{matrix}$ 为正整数)。

如果式(8)产生的新个体适应度值好于原个体, 则替代原个体, 否则随机生成新的个体进行替代。图2为优良群青蛙个体更新策略示意图。

	Figure Option View Download New Window
	图2 优良群青蛙个体更新策略Fig.2 Individual renewal strategy of fine group of frogs

2 压缩感知及信号重构

2.1 CS理论

CS原理可以描述为^[16]:

(1)假设有限长度为 $\begin{matrix} N 、 \end{matrix}$ 维数为1的离散信号 $\begin{matrix} x_{N \times 1} \end{matrix}$ 在空间正交基 $\begin{matrix} {ψ_{i}}_{i = 1}^{N} \end{matrix}$ 下可以用标准的正交基线性组合:

$\begin{matrix} x_{N \times 1} = Ψ_{N \times N} s_{N \times 1} (9) \end{matrix}$

式中: $\begin{matrix} Ψ_{N \times N} = [ψ_{1}, \dots, ψ_{N}] \end{matrix}$ 为表达基, 列向量 $\begin{matrix} s_{N \times 1} \end{matrix}$ 为正交基的加权系数。

(2)对 $\begin{matrix} x_{N \times 1} \end{matrix}$ 进行 $\begin{matrix} M (M ≪ N \end{matrix}$ )次线性测量, 可以描述为:

$\begin{matrix} y_{M \times 1} = Φ_{M \times N} x_{N \times 1} \overset{A_{M \times N} = Φ_{M \times N} Ψ_{N \times N}}{=} A_{M \times N} s_{N \times 1} = As (10) \end{matrix}$

式中: $\begin{matrix} Φ_{M \times N} \end{matrix}$ 为 $\begin{matrix} M \times N \end{matrix}$ 的测量基; $\begin{matrix} y_{M \times 1} \end{matrix}$ 为 $\begin{matrix} x_{N \times 1} \end{matrix}$ 的线性测量值。为了完整重构信号 $\begin{matrix} x_{N \times 1}, Φ_{M \times N} \end{matrix}$ 是与 $\begin{matrix} Ψ_{N \times N} \end{matrix}$ 不相关的测量基。

(3)信号 $\begin{matrix} s_{N \times 1} \end{matrix}$ 最小 $\begin{matrix} l_{0} \end{matrix}$ 范数求解, 即:

$\begin{matrix} \{\begin{matrix} \overset{\land}{s} = \min ‖ s ‖_{l_{0}} \\ s . t . y = As = ΦΨs \end{matrix} (11) \end{matrix}$

通过求解式(11)得到 $\begin{matrix} \overset{\land}{s}, \end{matrix}$ 进而通过式(9)实现对 $\begin{matrix} x_{N \times 1} \end{matrix}$ 的重构。

2.2 基于IDSFLA的CS稀疏重构

CS稀疏重构是指已知 $\begin{matrix} Ψ_{N \times N} 、 Φ_{M \times N} \end{matrix}$ 和 $\begin{matrix} y_{M \times 1}, \end{matrix}$ 求解稀疏向量 $\begin{matrix} s_{N \times 1} \end{matrix}$ 的过程。CS理论指出当 $\begin{matrix} A_{M \times N} \end{matrix}$ 满足RIP条件时, 通过求解最小 $\begin{matrix} l_{0} \end{matrix}$ 范数可以得到稀疏向量 $\begin{matrix} s_{N \times 1} \end{matrix}$ ^[17]。目前, 如何降低CS稀疏重构算法计算复杂度, 提高算法稳定性是核心研究内容。IDSFLA算法优秀的全局寻优能力为CS稀疏重构研究提供了新的思路, 本文提出了基于IDSFLA的压缩感知重构算法, 该重构算法不需要已知稀疏度, 将 $\begin{matrix} s_{N \times 1} \end{matrix}$ 理解为青蛙编码方式, 通过种群进化得到的全局最优解即为 $\begin{matrix} s_{N \times 1} \end{matrix}$ 中非零元素位置信息, 然后进一步利用最小二乘法最终获得非零元素位置的幅度信息。

定义8 IDSFLA目标函数。IDSFLA的目标函数定义为:

$\begin{matrix} minf (s) = ‖ y - ΦΨs ‖_{2}, \begin{matrix} s \in R^{N} \end{matrix} (12) \end{matrix}$

基于IDSFLA的CS稀疏重构算法实现过程可以描述为:

∥初始化

(1)算法参数设置。设置青蛙种群规模为N_f, 子族群数为Q_f, 全局最大进化代数为T_max, r_max, r_min, ξ ₁, ξ ₂以及其他参数。设定终止条件 $\begin{matrix} ‖ y - ΦΨs ‖_{2}^{2} \end{matrix}$ ≤ ε (ε 为极小数, 通常由实验确定)。

(2)初始化。对青蛙种群进行初始化, 计算青蛙个体适应度值f $\begin{matrix} (s_{i}) \end{matrix}$ , t← 0。

While (t≤ T_max) do

{

∥子族群划分

(3)按照适应度值对青蛙进行降序排列, 并对种群进行子族群划分。

(4)更新全局最优解P_g(t)及子族群最优解 $\begin{matrix} P_{B}^{l} \end{matrix}$ (t)(l=1, 2, …, Q_f)。

While (k≤ K_max) do

{

∥局部搜索

For i=1:Q_f

(5)根据式(4)(7)对子族群E_i进行改良群和优良群划分。

(6)改良群内个体根据式(5)更新, 优良群内个体根据式(8)进行更新。

(7)更新子族群E_i内的 $\begin{matrix} X_{w}^{i} \end{matrix}$ (t)和 $\begin{matrix} P_{B}^{i} \end{matrix}$ 。

(8)End

(9)k← k+1

}

∥全局信息交换

(10)将所有青蛙个体混合, 重新形成新的种群。

(11)更新全局最优解P_g(t)。

(12)终止条件判断, 如果 $\begin{matrix} ‖ y - ΦΨs ‖_{2}^{2} \end{matrix}$ ≤ ε 满足, 则终止算法输出结果, 否则t← t+1。

}

(13)程序结束, 输出结果。

2.3 WSNs多目标定位实现

问题描述。在被划分为 $\begin{matrix} N \end{matrix}$ 个网格的监控区域内, 部署 $\begin{matrix} M \end{matrix}$ 个位置已知的传感器, 监控区域中有 $\begin{matrix} K \end{matrix}$ 个未知目标(目标位置限定为网格中心)。设定目标位置向量为 $\begin{matrix} s = {[s_{1}, \dots, s_{j}, \dots s_{N}]}^{T}, \end{matrix}$ 当 $\begin{matrix} s_{j} = 1 \end{matrix}$ 表明网格 $\begin{matrix} j \end{matrix}$ 含有未知目标。 $\begin{matrix} K \end{matrix}$ 个目标的能量值为线性叠加, 因此传感器 $\begin{matrix} i \end{matrix}$ 处的能量 $\begin{matrix} x_{i} \end{matrix}$ 为:

$\begin{matrix} x_{i} = \overset{K}{\sum_{k = 1}} P_{i, k} + v_{i} (13) \end{matrix}$

式中: $\begin{matrix} v_{i} \end{matrix}$ 为高斯分布白噪声; $\begin{matrix} P_{i, k} \end{matrix}$ 为传感器 $\begin{matrix} i \end{matrix}$ 接收目标 $\begin{matrix} k 的信号强度, P_{i, k} = P_{0} G_{i, k} / d_{ik}^{α}; G_{i, k} \end{matrix}$ 为瑞利衰减, $\begin{matrix} d_{ik} \end{matrix}$ 为传感器 $\begin{matrix} i \end{matrix}$ 与目标 $\begin{matrix} k \end{matrix}$ 的欧拉距离。

$\begin{matrix} Ψ_{N \times N} \end{matrix}$ 与 $\begin{matrix} Φ_{M \times N} \end{matrix}$ 构造。当 $\begin{matrix} N \end{matrix}$ 个网格分别部署传感器时, $\begin{matrix} N \end{matrix}$ 个节点测量信号 $\begin{matrix} x_{N \times 1} = {[x_{1}, x_{2}, \dots, x_{N}]}^{T} \end{matrix}$ 为:

$\begin{matrix} \begin{matrix} [\begin{matrix} x_{1} \\ x_{2} \\ ⋮ \\ x_{N} \end{matrix}] = [\begin{matrix} \frac{P_{0} G_{1, 1}}{d_{11}^{α}} s_{1} + \dots + \frac{P_{0} G_{N, 1}}{d_{N 1}^{α}} s_{N} \\ \frac{P_{0} G_{1, 2}}{d_{12}^{α}} s_{1} + \dots + \frac{P_{0} G_{N, 2}}{d_{N 2}^{α}} s_{N} \\ ⋮ \\ \frac{P_{0} G_{1, N}}{d_{1 N}^{α}} s_{1} + \dots + \frac{P_{0} G_{N, N}}{d_{NN}^{α}} s_{N} \end{matrix}] = \\ [\begin{matrix} \frac{P_{0} G_{1, 1}}{d_{11}^{α}} & \frac{P_{0} G_{2, 1}}{d_{21}^{α}} & \dots & \frac{P_{0} G_{N, 1}}{d_{N 1}^{α}} \\ \frac{P_{0} G_{1, 2}}{d_{12}^{α}} & \frac{P_{0} G_{2, 2}}{d_{22}^{α}} & \dots & \frac{P_{0} G_{N, 2}}{d_{N 2}^{α}} \\ ⋮ ︙ & ⋮ & ⋮ \\ \frac{P_{0} G_{1, N}}{d_{1 N}^{α}} & \frac{P_{0} G_{2, N}}{d_{2 N}^{α}} & \dots & \frac{P_{0} G_{N, N}}{d_{NN}^{α}} \end{matrix}] [\begin{matrix} s_{1} \\ s_{2} \\ ⋮ \\ s_{N} \end{matrix}] = Ψs (14) \end{matrix} \end{matrix}$

从式(14)可以构造 $\begin{matrix} Ψ \end{matrix}$ 为稀疏矩阵。在实际测量过程中, 只需要 $\begin{matrix} M \end{matrix}$ 个传感器就可以实现定位, $\begin{matrix} M \end{matrix}$ 个传感器测量值 $\begin{matrix} y_{M \times 1} = {[y_{1}, y_{2}, \dots, y_{M}]}^{T} \end{matrix}$ 为:

$\begin{matrix} \begin{matrix} [\begin{matrix} y_{1} \\ y_{2} \\ ⋮ \\ y_{M} \end{matrix}] = [\begin{matrix} Φ_{1, 1} x_{1} + \dots + Φ_{N, 1} x_{N} \\ Φ_{1, 2} x_{1} + \dots + Φ_{N, 2} x_{N} \\ ⋮ \\ Φ_{1, M} x_{1} + \dots + Φ_{N, M} x_{N} \end{matrix}] = \\ [\begin{matrix} Φ_{1, 1} & Φ_{1, 2} & \dots & Φ_{1, N} \\ Φ_{2, 1} & Φ_{2, 2} & \dots & Φ_{2, N} \\ ⋮ & ⋮ & ⋮ \\ Φ_{M, 1} & Φ_{M, 2} & \dots & Φ_{M, N} \end{matrix}] [\begin{matrix} x_{1} \\ x_{2} \\ ⋮ \\ x_{N} \end{matrix}] = Φx \\ (15) \end{matrix} \end{matrix}$

$\begin{matrix} Φ_{i, j} = 1 \end{matrix}$ 表示网格 $\begin{matrix} i \end{matrix}$ 上存在传感器 $\begin{matrix} j, \end{matrix}$ 否则 $\begin{matrix} Φ_{i, j} = 0 。 \end{matrix}$ 构造 $\begin{matrix} Φ \end{matrix}$ 为测量矩阵。根据式(14)(15)有:

$\begin{matrix} y_{M \times 1} = Φx = ΦΨs \overset{A = ΦΨ}{=} As (16) \end{matrix}$

定理当传感器节点 $\begin{matrix} M = O (c (K + 1) \ln (N / K)) \end{matrix}$ 时, 矩阵 $\begin{matrix} A \end{matrix}$ 依概率 $\begin{matrix} 1 - φ \end{matrix}$ 满足于约束等距条件RIP。其中, $\begin{matrix} φ \in (0, 1), c = 8 / {γ^{2}}_{K} 。 \end{matrix}$

证明由于 $\begin{matrix} A = ΦΨ, \end{matrix}$ 因此有:

$\begin{matrix} A = P_{0} [\begin{matrix} G'_{11} / D_{11}^{α} & G'_{21} / D_{21}^{α} & \dots & G'_{N 1} / D_{N 1}^{α} \\ G'_{12} / D_{12}^{α} & G'_{22} / D_{22}^{α} & \dots & G'_{N 2} / D_{N 2}^{α} \\ ⋮ & ⋮ & ⋮ \\ G'_{1 M} / D_{1 M}^{α} & G'_{2 M} / D_{2 M}^{α} & \dots & G'_{NM} / D_{NM}^{α} \end{matrix}] (17) \end{matrix}$

式中: $\begin{matrix} D_{ij} \end{matrix}$ 表示第 $\begin{matrix} i \end{matrix}$ 个目标到 $\begin{matrix} j \end{matrix}$ 个传感器的欧拉距离。由于 $\begin{matrix} G'_{i j} \end{matrix}$ 为瑞利衰减, 因此有:

$\begin{matrix} G'_{ij} = G'_{ij, r} + i \times G'_{ij, i} \to A = A_{r} + i \times A_{i} (18) \end{matrix}$

式中: $\begin{matrix} G'_{ij, r} 、 G'_{ij, i} \end{matrix}$ 分别对应相应的实部; $\begin{matrix} A_{r} 、 A_{i} \end{matrix}$ 分别为对应相应的虚部, 而且 $\begin{matrix} G'_{ij, r} ~ N (0, ζ_{}^{2}) \end{matrix}$ 和 $\begin{matrix} G'_{ij, i} ~ N (0, ζ_{}^{2}) 。 \end{matrix}$ 显然当 $\begin{matrix} A_{r} (A_{i} \end{matrix}$ )满足RIP条件时, 矩阵 $\begin{matrix} A \end{matrix}$ 就满足RIP条件。对于矩阵 $\begin{matrix} A_{r} \end{matrix}$ 第 $\begin{matrix} i \end{matrix}$ 行 $\begin{matrix} A_{r}^{i} = P_{0} [\begin{matrix} G'_{1 i} / D_{1 i}^{α} & G'_{2 i} / D_{2 i}^{α} & \dots & G'_{Ni} / D_{N i}^{α} \end{matrix}], \end{matrix}$ 对其进行归一化处理, 即:

$\begin{matrix} \begin{matrix} < A_{r}^{i} > = \\ μ < \begin{matrix} P_{0} G'_{1 i} / D_{1 i}^{α} & P_{0} G'_{2 i} / D_{2 i}^{α} & \dots & P_{0} G'_{Ni} / D_{Ni}^{α} \end{matrix} > (19) \end{matrix} \end{matrix}$

式中: $\begin{matrix} μ \end{matrix}$ 为归一化常数。

$\begin{matrix} μ = \sqrt[]{N (M \overset{N}{\sum_{j = 1}} P_{0}^{2} ζ_{}^{2} / D_{ij}^{2 α})} (20) \end{matrix}$

对于稀疏向量 $\begin{matrix} s = {[s_{1}, s_{2}, \dots, s_{N}]}^{T}, \end{matrix}$ 其与 $\begin{matrix} A_{r}^{i} \end{matrix}$ 的乘积为高斯分布, 即:

$\begin{matrix} A_{r}^{i} s ~ N (0, δ_{1}^{2}), δ_{1}^{2} = K μ^{2} (\overset{N}{\sum_{j = 1}} P_{0}^{2} ζ_{}^{2} / D_{ij}^{2 α}) / N (21) \end{matrix}$

令 $\begin{matrix} X_{i} = A_{r}^{i} s, \end{matrix}$ 则有 $\begin{matrix} ‖ A_{r} s ‖_{2}^{2} = X_{1}^{2} + \dots + X_{M}^{2}, \end{matrix}$ 因此, $\begin{matrix} ‖ A_{r} s ‖_{2}^{2} ~ χ (M), \end{matrix}$ 且 $\begin{matrix} E (‖ A_{r} s ‖_{2}^{2}) = M δ_{1}, D (‖ A_{r} s ‖_{2}^{2}) = 2 M δ_{1}^{4} 。 \end{matrix}$ 当 $\begin{matrix} M \end{matrix}$ 取较大值时, $\begin{matrix} ‖ A_{r} s ‖_{2}^{2} / ‖ s ‖_{2}^{2} \end{matrix}$ 服从高斯分布, 其方差为:

$\begin{matrix} D (‖ A_{r} s ‖_{2}^{2} / ‖ s ‖_{2}^{2}) = 2 M δ_{1}^{4} / K^{2} = 2 / M (22) \end{matrix}$

由Chernoff不等式得:

$\begin{matrix} P \{|1 - ‖ A_{r} s ‖_{2}^{2} / ‖ s ‖_{2}^{2}| > γ_{K}\} \leq 2 e^{- γ_{K}^{2} M / 8} (23) \end{matrix}$

对于矩阵 $\begin{matrix} A_{r} \end{matrix}$ 的 $\begin{matrix} K \end{matrix}$ 为子空间总数为:

$\begin{matrix} (\begin{matrix} N \\ K \end{matrix}) \leq {(eN / K)}^{K} (24) \end{matrix}$

因此, 任取稀疏向量 $\begin{matrix} s \end{matrix}$ 有:

$\begin{matrix} \begin{matrix} P \{|1 - ‖ A_{r} s ‖_{2}^{2} / ‖ s ‖_{2}^{2}| > γ_{K}\} \leq \\ 2 e^{- γ_{K}^{2} M / 8} {(eN / K)}^{K} = 2 e^{^{\frac{- γ_{K}^{2} M}{8} + Kln (\frac{N}{K}) + K}} (25) \end{matrix} \end{matrix}$

定义 $\begin{matrix} u_{φ} \end{matrix}$ 为指数函数 $\begin{matrix} f (x) = e^{x} \end{matrix}$ 下侧分位数, 即: $\begin{matrix} P \{x \leq u_{φ}\} = φ \end{matrix}$ (本文中 $\begin{matrix} φ \in (0, 1), \end{matrix}$ 因此 $\begin{matrix} u_{φ} < 0) 。 \end{matrix}$ 结合式(25), 当 $\begin{matrix} \frac{M γ_{K}^{2}}{8} - Kln (\frac{N}{K}) - K \geq |u_{φ}| \end{matrix}$ 成立时, $\begin{matrix} P {|1 - ‖ A_{r} s ‖_{2}^{2} / ‖ s ‖_{2}^{2}| > γ_{K}} \leq φ, \end{matrix}$ 即当 $\begin{matrix} M \geq \frac{8}{γ_{K}^{2}} [(K + 1) (\frac{N}{K}) + |u_{φ}|] \end{matrix}$ 时, $\begin{matrix} P \{|1 - ‖ A_{r} s ‖_{2}^{2} / ‖ s ‖_{2}^{2}| \leq γ_{K}\} \geq 1 - φ 。 \end{matrix}$ 因此, 当 $\begin{matrix} M = O (c (K + 1) \ln (N / K)) \end{matrix}$ 时( $\begin{matrix} c = 8 / γ_{K}^{2}), \end{matrix}$ 矩阵 $\begin{matrix} A \end{matrix}$ 依概率 $\begin{matrix} 1 - φ \end{matrix}$ 满足于约束等距条件RIP, 当 $\begin{matrix} φ \leq 0.05 \end{matrix}$ 时, 矩阵 $\begin{matrix} A \end{matrix}$ 满足约束等距条件的概率在95%以上。证毕。

这样证明了 $\begin{matrix} A = ΦΨ \end{matrix}$ 满足RIP条件, 所以WSNs目标定位问题能够转化为CS重构问题, 可以采用基于IDSFLA的CS稀疏重构算法得到目标位置向量 $\begin{matrix} s_{N \times 1} 。 \end{matrix}$

3 算例分析及仿真

3.1 IDSFLA算法性能验证

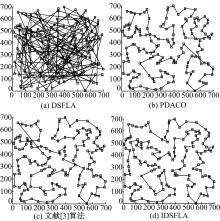
IDSFLA参数设置如下: $\begin{matrix} N_{f} = 200; Q_{f} = 20; q = 10; K_{\max} = 10; T_{\max} = 500; r_{\max} = 0.8; r_{\min} = 0.2; ε = 10^{- 4}; τ = 0.6 。 \end{matrix}$ 分别采用DSFLA、PDACO^[18]、文献[3]算法和IDSFLA对TSPLIB中的bayg29、eil51和ch150进行测试。仿真测试环境设置及算法参数设置参考第三节相关设置。每种算法独立重复运行50次, 取平均距离 $\begin{matrix} \bar{S} 、平均运算时间 \bar{t} \end{matrix}$ 和相对误差Err等指标进行对比, 其中, Err计算公式为:

$\begin{matrix} Err = (\bar{S} - Opt) / Opt (26) \end{matrix}$

式中:Opt为已知全局最优环路长度(bayg29、eil51和ch150理论最优路线长度分别为9074.1, 428.87和6528), 表1给出了具体实验结果数据。图3为ch150问题下4种算法给出的最优行进路线。

表1 TSPLIB不同算法测试结果 Table 1 Test results for different TSPLIB algorithm

算法	指标	bayg29	eil51	ch150
DSFLA	$\begin{matrix} \bar{S} \end{matrix}$	16513.7	1227.6	46210.3
	$\begin{matrix} \bar{t} \end{matrix}$	6.11	12.71	27.16
	Err/%	81.9	186.2	607.9
PDACO	$\begin{matrix} \bar{S} \end{matrix}$	10231.1	511.6	7001.2
	$\begin{matrix} \bar{t} \end{matrix}$	7.13	14.18	30.22
	Err/%	12.8	19.4	7.2
文献[3]	$\begin{matrix} \bar{S} \end{matrix}$	9978.4	477.8	6892.1
	$\begin{matrix} \bar{t} \end{matrix}$	5.26	10.17	25.39
	Err/%	9.9	11.4	5.6
IDSFLA	$\begin{matrix} \bar{S} \end{matrix}$	9107.2	431.2	6577.1
	$\begin{matrix} \bar{t} \end{matrix}$	4.21	7.32	12.17
	Err/%	0.4	0.7	0.8

表1 TSPLIB不同算法测试结果 Table 1 Test results for different TSPLIB algorithm

	Figure Option View Download New Window
	图3 ch150问题最优行进路线Fig.3 Optimal routes of ch150 problem

在算法求解精度方面, PDACO、文献[3]算法和IDSFLA都能够给出较好的行进路线, 且IDSFLA的求解精度明显优于其他两种算法, 而DSFLA无法得到最优解。在算法运行速度方面, 对于bayg29、eil51和ch150测试问题, IDSFLA运算速度都要快于其他3种算法。

3.2 WSNs多目标定位仿真

30 m× 30 m监控区域被划分为900个网格, 设共有35个未知目标, 即重构信号稀疏度为35, 部署120个传感器, SNR=20 dB(噪声级别), 利用衰减模型生成测量矩阵。分别采用GMP、ROMP和基于IDSFLA的CS稀疏重构算法(记为IDSFLAMP)进行目标定位, 分别运行30次, 取算法平均消耗时间 $\begin{matrix} \bar{T} \end{matrix}$ 和文献[12]给出的目标定位失效率(POF)及目标定位误差(RMSE)指标进行对比, 表2给出了测试结果。

从测试结果可看出, IDSFLA目标定位精度优于其他两种算法, 且具有较低的定位失效率, 而GMP定位精度最差, 定位失误率达到了27%, 在算法运算时间方面, 由于IDSFLAMP采取多次循环迭代机制, 算法运算时间相对较长。

表2 目标定位测试结果 Table 2 Target location test results

算法	RMSE/m	$\begin{matrix} \bar{T} \end{matrix}$ /s	POF/%
GMP	0.69	0.31	27
ROMP	0.72	0.59	14
IDSFLA	0.15	1.02	3

表2 目标定位测试结果 Table 2 Target location test results

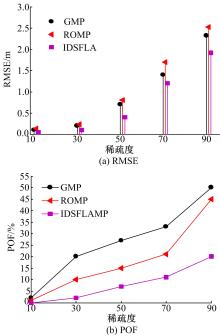
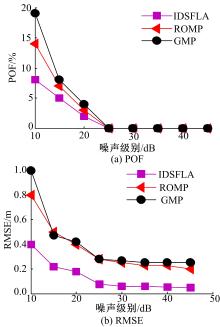
为了进一步分析IDSFLAMP算法性能, 分别设置不同稀疏度、噪声级别等参数进行实验仿真。图4给出了不同稀疏度下算法定位性能对比。由图4可以看出, 图5给出了不同噪声级别下的GMP、ROMP和IDSFLAMP算法定位性能对比。

	Figure Option View Download New Window
	图4 不同稀疏度下算法定位性能Fig.4 Algorithm positioning performance under different sparse degrees

	Figure Option View Download New Window
	图5 不同噪声级别下算法定位性能Fig.5 Algorithm positioning performance under different noise levels

当稀疏度在30以下时, GMP、ROMP和IDSFLAMP算法都能准确完成目标定位, 且定位精度相对较高, 随着稀疏度不断增加, 3种算法定位性能明显下降, 特别地当稀疏度低于50时, IDSFLAMP算法仍可以以较高准确率实现目标定位。

由图5可以看出, 当噪声为25~45 dB时, 3种算法都能够完成目标定位, 表明3种算法具有一定的抗噪能力, 而且对于不同噪声级别, IDSFLAMP算法定位性能优于其他两种算法。

4 结束语

研究了改进的离散混合蛙跳算法及在压缩感知重构算法中的应用。仿真结果表明, 改进的离散混合蛙跳算法具有优异的复杂问题求解能力, 基于改进DSFLA压缩感知重构算法的WSNs目标定位精度优于传统GMP、ROMP重构算法, 且在噪声级别25 dB下能够准确、稳定地实现目标定位。下一步需要重点研究离散智能算法基本理论及压缩感知重构算法的稳定性和鲁棒性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	任哲, 周本达, 陈明华. 一种基于随机化均匀设计点集的遗传算法用于求解MVCP[J]. 模式识别与人工智能, 2010, 23(2): 284-288. Ren Zhe, Zhou Ben-da, Chen Ming-hua. Genetic algorithm for solving a rand om set of uniform design point MVCP[J] Pattern Recognition and Artificial Intelligence, 2010, 23(2): 284-288. [本文引用:1]
[2]	Eusuff M M, Lansey K E. Optimization of water distribution network design using the shuffled frog leaping algorithm[J]. Water Resources Planning and Management, 2003, 129(3): 210-225. [本文引用:1]
[3]	李建军, 郁滨, 陈武平. 混合蛙跳算法的改进与仿真[J]. 系统仿真学报, 2014, 26(4): 755-760. Li Jian-jun, Yu Bin, Chen Wu-ping. SFLA Improvement and simulation[J]. Journal of System Simulation, 2014, 26(4): 755-760. [本文引用:1]
[4]	骆剑平, 李霞, 陈泯融. 基于改进混合蛙跳算法的CVRP求解[J]. 电子与信息学报, 2011, 33(2): 429-434. Luo Jian-ping, Li Xia, Chen Min-rong. Obliterate the CVRP solving based on SFLA[J]. Journal of Electronics and Information Technology, 2011, 33(2): 429-434. [本文引用:1]
[5]	肖莹莹, 柴旭东, 李伯虎, 等. 混合蛙跳算法的收敛性分析及其改进[J]. 华中科技大学学报: 自然科学版, 2012, 40(7): 15-18. Xiao Ying-ying, Chai Xu-dong, Li Bo-hu, et al. Convergence of SFLA its improvement[J]. Huazhong University of Science and Technology (Natural Science), 2012, 40(7): 15-18. [本文引用:1]
[6]	Donoho D. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. [本文引用:1]
[7]	孔繁锵, 井庆丰, 计振兴. 图像压缩感知的自适应方向提升稀疏表示及重构算法[J]. 宇航学报, 2013, 34(1): 121-127. Kong Fan-qiang, Jing Qing-feng, Ji Zhen-xing. Revitalization of adaptive image compression direction to enhance the perception sparse representation and reconstruction algorithm[J]. Journal of Astronautics, 2013, 34(1): 121-127. [本文引用:1]
[8]	练秋生, 陈书贞. 基于解析轮廓波变换的图像稀疏表示及其在压缩传感中的应用[J]. 电子学报, 2010, 38(6): 1293-1298. Lian Qiu-sheng Chen Shu-zhen. Representation image sparse profile based on analytic wavelet transform in compressed sensing[J]. Journal of Electronics, 2010, 38(6): 1293-1298. [本文引用:1]
[9]	Peyré G. Best basis compressed sensing[J]. IEEE Transactions on Signal Processing, 2010, 58(5): 2613-2622. [本文引用:1]
[10]	彭向东, 张华, 刘继忠. 基于过完备字典的体域网压缩感知心电重构[J]. 自动化学报, 2014, 40(7): 1421-1432. Peng Xiang-dong, Zhang Hua, Liu Ji-zhong. Had complete dictionary based on body area network compressed sensing cardiac remodeling[J]. Automatica Sinica, 2014, 40(7): 1421-1432. [本文引用:1]
[11]	张宗念, 黄仁泰, 闫敬文. 压缩感知信号盲稀疏度重构算法[J]. 电子学报, 2011, 39(1): 18-22. Zhang Zong-nian, Huang Ren-tai, Yan Jing-wen. Compressed sensing reconstruction algorithm for blind signal sparsity[J]. Acta Electronica, 2011, 39(1): 18-22. [本文引用:1]
[12]	刘洲洲, 王福豹. 基于离散萤火虫压缩感知重构的无线传感器网络多目标定位[J]. 光学精密工程, 2014, 22(7): 1904-1911. Liu Zhou-zhou, Wang Fu-bao. Reconstruction discrete wireless sensor networks multi-objective positioning based on compressed sensing[J]. Optics and Precision Engineering, 2014, 22(7): 1904-1911. [本文引用:1]
[13]	周永权, 黄正新, 刘洪霞. 求解TSP问题的离散型萤火虫群优化算法[J]. 电子学报, 2012, 40(6): 1164-1170. Zhou yong-quan, Huang Zheng-xin, Liu Hong-xia. Discrete glowworm swarm optimization algorithm for solving TSP[J]. Acta Electronica Sinica, 2012, 40(6): 1164-1170. [本文引用:1]
[14]	姜建国, 张丽媛, 苏仟, 等. 一种利用动态搜索策略的混合蛙跳算法[J]. 西安电子科技大学学报: 自然科学版, 2014, 41(4): 51-57. Jiang Jian-guo, Zhang Li-yuan, Su Qian, et al. A shuffled frog leaping algorithm by dynamic search strategy[J]. Journal of Xi'an Electronic and Science University (Natural Science Edition), 2014, 41(4): 51-57. [本文引用:1]
[15]	郑仕链, 楼才义, 杨小牛. 基于改进混合蛙跳算法的认知无线电协作频谱感知[J]. 物理学报, 2010, 59(5): 3611-3616. Zheng Shi-lian, Lou Cai-yi, Yang Xiao-niu. An improved shuffled frog leaping algorithm for cooperative spectrum sensing in cognitive radio networks based on[J]. Acta Physica Sinica, 2010, 59(5): 3611-3616. [本文引用:1]
[16]	石光明, 刘丹华, 高大化, 等. 压缩感知理论及其研究进展[J]. 电子学报, 2009, 37(5): 1070-1081. Shi Guang-ming, Liu Dan-hua, Gao Da-hua, et al. Theory and research progress compressed sensing[J]. Journal of Electronics, 2009, 37(5): 1070-1081. [本文引用:1]
[17]	何风行, 余志军, 刘海涛. 基于压缩感知的无线传感器网络多目标定位算法[J]. 电子与信息学报, 2012, 34(3): 716-721. He Feng-xing, Yu Zhi-jun, Liu Hai-tao. Wireless sensor networks based on the compressed sensing in multi target locating algorithm[J]. Journal of Electronics and Information Technology, 2012, 34(3): 716-721. [本文引用:1]
[18]	黄国锐, 曹先彬, 王煦法. 基于信息素扩散的蚁群算法[J]. 电子学报, 2004, 32(5): 865-868. Huang Guo-rui, Cao Xian-bin, Wang Xu-fa. Pheromone diffusion method based on ant colony algorithm[J]. Journal of Electronics, 2004, 32(5): 865-868. [本文引用:1]

2010

0.0

. 2010, 23(2):284-288 DOI:doi:10.3969/j.issn.1003-6059.2010.02.023

Genetic algorithm for solving a random set of uniform design point MVCP

一种基于随机化均匀设计点集的遗传算法用于求解MVCP

Ren Zhe , Zhou Ben-da , Chen Ming-hua.

任哲, 周本达, 陈明华

Based on the mechanism analysis of ideal density model and by utilizing the principle and method of random uniform design (RUD), the crossover operation in genetic algorithm (GA) is redesigned. Then, on the basis of characteristic analysis of the minimum vertices covering problem (MVCP) in graph and combining scan-repair and local improvement techniques, a GA based on RUD point set is presented to solve the MVCP. Compared with simple GA and Good Point GA for solving this problem, the simulation results show that the presented GA has superiority in speed, accuracy and overcoming premature.

基于理想浓度模型的机理分析，利用随机化均匀设计的理论和方法，对遗传算法中的交叉操作进行重新设计，并在分析图最小顶点覆盖问题特点的基础上，结合扫描-修正和局部改进策略，给出一个解决图最小顶点覆盖问题的遗传算法，称之为基于随机化均匀设计点集的遗传算法。通过将该算法与简单遗传算法和佳点集遗传算法进行求解图最小顶点覆盖问题的仿真模拟比较，可看出该算法提高求解的质量、速度和精度。

... 0 引言由于工程实际问题通常具有大规模、非线性、建模困难等特点,传统的优化算法在求解精度、求解效率等方面已不能有效解决,因此寻求适用于大规模并行计算的智能优化方法成为当前研究热点之一^[1] ...

2003

0.0

... 2003年,学者Eusuff和Lansey^[2]通过模拟青蛙群体觅食行为,提出了一种新的启发式智能计算技术#cod#x02014 ...

2014

0.0

. 2014, 26(4):755-760

SFLA Improvement and simulation

混合蛙跳算法的改进与仿真

Li Jian-jun , Yu Bin , Chen Wu-ping.

李建军, 郁滨, 陈武平

摘　要：针对传统混合蛙跳算法在寻优过程中收敛速度慢且易陷入局部最优的问题,提出一种改进的混合蛙跳算法。该算法对传统混合蛙跳算法的组内更新策略进行重新设计,使其具有组内最佳更新位置记忆功能,同时在全组牵引步长的基础上,使用随机双向更新的方式。通过对6个标准函数的四组实验,结果表明该算法在收敛速度、跳出局部最优能力以及收敛精度上都有很大提高,与其他算法相比具有更强的求解能力。最后针对作业车间调度问题进行了仿真实验。

... 混合蛙跳算法(Shuffled frog leaping algorithm,SFLA),算法按照子种群划分思想更新青蛙模因信息,实现了局部搜索与全局信息交换有机结合,具有较强的鲁棒性^[3] ...

2011

0.0

. 2011, 33(2):429-434 DOI:doi:10.3724/SP.J.1146.2010.00328

Obliterate the CVRP solving based on SFLA

基于改进混合蛙跳算法的CVRP求解

Luo Jian-ping , Li Xia , Chen Min-rong.

骆剑平, 李霞, 陈泯融

An improved Shuffled Frog Leaping Algorithm (SFLA) is proposed to solve the Capacitated Vehicle Routing Problem(CVRP)based on real-coded patterns. It is then combined with the power-law Extremal Optimization (τ-EO) to further improve the local search ability. The fitness for the components of an individual is carefully designed and the neighborhood for τ-EO mutation is established according to power-law probability distribution. Experimental results show that the proposed algorithm outperforms other heuristic algorithms base on PSO and GA.

该文提出基于实数编码模式的混合蛙跳算法(Shuffled Frog Leaping Algorithm，SFLA)求解容量约束车辆路径问题(Capacitated Vehicle Routing Problem，CVRP)；把具有极强局部搜索能力的幂律极值动力学优化(Power Law Extremal Optimization，τ-EO)融合于SFLA，针对CVRP对τ-EO过程进行设计和改进。改进的τ-EO采用新颖的组元适应度计算方法；采用幂律概率分布来挑选需要变异的组元；根据最邻近城市表，采用幂律概率分布挑选变异组元的最佳邻近城市，执行线路间或线路内的变异。求解测试库中的实例，证明该改进算法有效。

... 目前,关于混合蛙跳算法的研究主要集中于算法改进和在连续优化问题中的应用等方面^[4,5],关于离散混合蛙跳算法的研究则相对较少,且缺乏相对系统的理论研究,因此,开展离散混合蛙跳算法研究具有重要意义 ...

2012

0.0

. 2012, 40(7):15-18

Convergence of SFLA its improvement

混合蛙跳算法的收敛性分析及其改进

Xiao Ying-ying , Chai Xu-dong , Li Bo-hu

肖莹莹, 柴旭东, 李伯虎

在分析混合蛙跳算法(SFL)收敛性的基础上,针对早熟收敛和收敛速度慢的问题,提出一种改进算法(MSFL).MSFL利用变公比数列分析更新轨迹的收敛性,并引入离散度和适应度方差作为指标,自适应地调节数列公比取值范围,以平衡收敛精度和收敛速度.以6个Benchmark函数分2组实验,测试MSFL的性能.结果表明:提出的MSFL算法具有较强的全局搜索和局部搜索能力,且具有收敛速度快、收敛精度高的优点.

2006

0.0

... 压缩感知(Compressed sensing,CS)^[6]是一种新型的数据压缩和重构理论,具有编码简单、抗误码性好、能够实现高效的压缩等特点^[7],为无线传感器网络(WSNs)、图像处理、目标跟踪等领域提供了全新的解决问题的思路^[8,9,10] ...

2013

0.0

. 2013, 34(1):121-127 DOI:doi:10.3873/j.issn.1000-1328.2013.01.017

Revitalization of adaptive image compression direction to enhance the perception sparse representation and reconstruction algorithm

图像压缩感知的自适应方向提升稀疏表示及重构算法

Kong Fan-qiang , Jing Qing-feng , Ji Zhen-xing.

孔繁锵, 井庆丰, 计振兴

To overcome the poor directional selectivity of orthogonal wavelet bases, signal energy is made more sparse by selecting the filters in different texture regions for image signal direction, an image compressed sensing reconstruction algorithm based on an adaptive directional lifting sparse representation is presented. After each iterative refinement in the reconstruction, the signal energy distribution is more concentrated by selecting wavelet bases with different intensities of the direction and signal smoothness according to the texture characteristics of the image signal, and a wavelet thresholding method is used to realize signal reconstruction denoising. Experimental results show that the proposed algorithm improves the peak signal to noise ratio and visual quality, and protects image details.

为了克服传统的压缩感知重构中正交小波方向选择性差的局限性，针对图像信号方向性决定了需要在不同纹理区域选择滤波器以使变换后信号能量更加稀疏，提出一种基于自适应方向提升稀疏表示的重构方法。重构时，在每次迭代更新后，根据图像信号的纹理特征选择不同强度方向和信号光滑度的小波基，使得变换后信号能量分布更加集中，并利用小波域阈值处理方法解决信号的重构噪声问题。实验结果表明，该算法提高了重构图像的峰值信噪比和视觉效果，保护了图像的细节。

2010

0.0

. 2010, 38(6):1293-1298

Representation image sparse profile based on analytic wavelet transform in compressed sensing

基于解析轮廓波变换的图像稀疏表示及其在压缩传感中的应用

Lian Qiu-sheng Chen Shu-zhen

练秋生, 陈书贞

The translation invariant analytic contourlet transform with low redundancy is proposed. In this transform, the circular symmetric filter banks decomposes image into multi-resolution detail subbands and one low-frequency subband, then the detail subbands are processed by Hilbert transform to generate two dimensional analytic signals. At last, the analytic signals are decomposed by directional filter bank to implement analytic contourlet transform with multi-scale, multi-direction, and translation invariant property. The real part and imaginary part of the analytic contourlet basis functions resemble Gabor wavelet, and conform well to the human visual system. The experiments show that the analytic contourlet transform can achieve higher performance in image denoising and compressed sensing.

提出了具有平移不变性的低冗余度解析轮廓波变换.在该变换中圆对称滤波器组首先将图像分解为多个不同分辨率的细节子带和一个低频子带,再对细节子带进行希尔伯特变换形成二维解析信号.最后用方向滤波器组对二维解析信号进行分解，实现具有平移不变性多尺度多方向的解析轮廓波变换.解析轮廓波变换基函数的实部和虚部与Gabor小波的实部和虚部类似，符合人眼视觉特性.实验结果表明解析轮廓波变换在图像去噪和压缩传感方面具有明显优势.

2010

0.0

2014

0.0

. 2014, 40(7):1421-1432 DOI:doi:10.3724/sp.j.1004.2014.01421

Had complete dictionary based on body area network compressed sensing cardiac remodeling

基于过完备字典的体域网压缩感知心电重构

Peng Xiang-dong , Zhang Hua , Liu Ji-zhong.

彭向东, 张华, 刘继忠

Regarding to tackle the problem of demanding high accuracy reconstruction electrocardiogram (ECG) signal in a remote monitoring center of the body sensor network (BSN) and the low power problem of the body sensor network, this paper proposes a method of ECG reconstruction of body sensor network using compressed sensing based on overcomplete dictionary. The proposed method uses the compressed sensing theory and random binary matrices as the sensing matrix to measure the ECG signal on the sensor nodes. After the measured value is transmitted to the remote monitoring center, the overcomplete dictionary based on K-SVD algorithm training and the block sparse Bayesian learning reconstruction algorithm are used to reconstruct the ECG signal. Simulation results show that the SNR of the compressed sensing reconstruction ECG based on K-SVD overcomplete dictionary method is 5～22dB higher than that of the method using discrete cosine transform when the ECG signal compression rate is at 70%～95%．The method has the advantages of high accuracy of signal reconstruction, low power, and easy hardware implementation.

针对体域网远程监护中心对重构的心电信号（Electrocardiogram，ECG）精度要求高和体域网（Body sensor network，BSN）低功耗问题，提出基于过完备字典的体域网压缩感知心电重构方法. 该方法利用压缩感知理论，在传感节点端利用随机二进制矩阵对心电信号进行观测，观测值被传送至远程监护中心后，再利用基于K-SVD算法训练得到的过完备字典和块稀疏贝叶斯学习重构算法对心电信号进行重构. 仿真结果表明，当心电信号压缩率在70%～95%时，基于K-SVD过完备字典比基于离散余弦变换基的压缩感知心电重构信噪比高出5～22dB. 该方法具有信号重构精度高、功耗低和易于硬件实现的优点.

2011

0.0

. 2011, 39(1):18-22

Compressed sensing reconstruction algorithm for blind signal sparsity

压缩感知信号盲稀疏度重构算法

Zhang Zong-nian , Huang Ren-tai , Yan Jing-wen.

张宗念, 黄仁泰, 闫敬文

A new blind sparsity iterative greedy reconstruction algorithm is presented based on studying the signal reconstruction algorithm for compressed sensing without the prior information of signal sparsity.A stage-wised and backtracking method is employed to adaptively adjust the candidate list at each iteration in order to estimate the true supporting set of the approximated signal.The theoretical analysis and experiment simulation prove that the performance of the algorithm outperforms that of the existing state-of-art iterative greedy matching pursuit algorithms,and provides a generalized greedy reconstruction framework.The orthogonal matching pursuit and subspace pursuit can be viewed as its special case,and it also gives the best trade-offs between computational complexity and reconstruction performance.This makes it a promising candidate for many practical applications for compressed sensing signal reconstruction.

研究压缩感知信号重构算法,提出了一种不需要精确知道信号稀疏度的先验知识,就能重构出目标信号的盲稀疏度迭代贪婪跟踪重构新算法.采用分段的方法来逐段估计、扩充目标信号的真实支撑域,并应用后向追踪思想,自适应地调整候选序列,以便每一次迭代时更加精确地估计真正的支撑域.理论分析与实验证明,算法性能超过了现有的迭代贪婪跟踪重构算法性能;给出了迭代贪婪跟踪信号重构的统一框架,正交匹配跟踪和子空间跟踪算法可以看成它的特例;在计算复杂度和重构算法性能之间做出了最佳折衷;有更强的实用性.

2014

0.0

. 2014, 22(7):1904-1911 DOI:doi:10.3788/OPE.20142207.1904

Reconstruction discrete wireless sensor networks multi-objective positioning based on compressed sensing

基于离散萤火虫压缩感知重构的无线传感器网络多目标定位

Liu Zhou-zhou , Wang Fu-bao.

刘洲洲, 王福豹

研究了压缩感知（CS）理论在无线传感器网络（WSNs）多目标定位中的应用。提出一种基于离散萤火虫算法的压缩感知重构方法，并设计了具体算法实现流程，该算法摆脱了传统压缩感知重构算法对稀疏度的依赖且能够准确地重构出原始信号。基于此，将新的压缩感知重构算法应用于WSNs目标定位，建立了WSNs系统模型，构造了合理的测量矩阵和稀疏矩阵，并分析了测量矩阵与重构结果之间的关系，最终实现了WSNs多目标定位。仿真结果表明该方法在稀疏信号重构性能及多目标定位精度方面具有较好效果，定位精度优于贪婪匹配跟踪（GMP）算法、正交匹配追踪（OMP）算法和最大似然估计（MLE）算法，且用于WSNs定位的传感器节点数目减少了20%，抗噪性达到了20 dB。

2012

0.0

. 2012, 40(6):1164-1170 DOI:doi:10.3969/j.issn.0372-2112.2012.06.016

Discrete glowworm swarm optimization algorithm for solving TSP

求解TSP问题的离散型萤火虫群优化算法

Zhou yong-quan , Huang Zheng-xin , Liu Hong-xia

周永权, 黄正新, 刘洪霞

A discrete glowworm swarm optimization (DGSO) algorithm is designed to tackle the travelling salesman problem.A new encoding schema and decoding schema are given with the characteristics of the TSP problem,and a new distance formula and encoding update formula for the new algorithm are given.In order to enhance the capability of the algorithm local searching,and to speed up the algorithm convergence speed,the 2-opt local search scheme is integrated into the new algorithm for solving TSP problem.The proposed algorithm was evaluated on 10 TSP test problems.The numerical experiments show that the proposed algorithm can find the global optimal solution with less computation and evolving time.In case of large scale TSP algorithm can achieve optimal solution of the theory and the error of the optimal solution is also less than 1%.

基于求解TSP问题,提出一种离散型萤火虫群优化(DGSO)算法,该算法结合TSP问题特点,给出一种有效编码和解码方法,并定义适合编码的个体间距离计算公式和编码更新公式.同时,为增强算法求解TSP问题的局部搜索能力,加快算法的收敛速度,算法使用了操作简单的2-Opt优化算子.最后,通过对10个TSP问题进行仿真实验,实验结果表明本文提出的算法是在种群规模较小,迭代次数较少的情况下就可以收敛到已知最优解.在大规模TSP算例中算法获得的最优值与理论最优值的误差也在1%以下.

... 在智能优化算法中,每个粒子编码代表问题的一个解^[13,14],因此,粒子的编码方式及相应的编码更新机制直接决定了算法能否高效解决离散优化问题 ...

2014

0.0

. 2014, 41(4):51-57 DOI:doi:10.3969/j.issn.1001-2400.2014.04.010

A shuffled frog leaping algorithm by dynamic search strategy

一种利用动态搜索策略的混合蛙跳算法

Jiang Jian-guo , Zhang Li-yuan , Su Qian

姜建国, 张丽媛, 苏仟

从混合蛙跳算法的寻优原理出发，研究了其寻优机制。针对标准算法中存在的初始种群不均匀、迭代后期收敛速度慢，易陷入局部最优的缺陷，提出了一种改进的混合蛙跳算法。采用随机化均匀设计方法产生初始种群；引入影响因子，动态地改变子群当前最差值对其进化行为的影响；根据群体适应度方差判断种群是否陷入局部最优，并通过对当前全局最优值微扰，使算法跳出局部最优。实验结果表明，改进算法有更高的收敛精度和更好的收敛结果。

... 在智能优化算法中,每个粒子编码代表问题的一个解^[13,14],因此,粒子的编码方式及相应的编码更新机制直接决定了算法能否高效解决离散优化问题 ...

2010

0.0

. 2010, 59(5):3611-3616

An improved shuffled frog leaping algorithm for cooperative spectrum sensing in cognitive radio networks based on

基于改进混合蛙跳算法的认知无线电协作频谱感知

Zheng Shi-lian , Lou Cai-yi , Yang Xiao-niu.

郑仕链, 楼才义, 杨小牛

A modified shuffled frog leaping algorithm (SFLA) and cooperative spectrum sensing for cognitive radios based on the modified SFLA are proposed. Simulations are performed to compare the performance of the modified SFLA and traditional SFLA. The performance of the proposed cooperative spectrum sensing method based on the modified SFLA and that of the cooperative spectrum sensing method using modified deflection coefficient (MDC) are also compared. Results show that the proposed SFLA outperforms the traditional SFLA, and the proposed cooperative spectrum sensing method based on the modified SFLA gives higher detection probability than the MDC-based method, which validates the effectiveness of the modified SFLA-based cooperative sensing method.

提出了一种改进的混合蛙跳算法（shuffled frog leaping algorithm，SFLA），并提出了基于改进SFLA的认知无线电协作频谱感知方法，通过仿真对改进SFLA算法性能与传统SFLA算法性能进行了比较，并对本文提出的基于改进SFLA的协作感知方法与已有的基于修正偏差因子（modified deflection coefficient，MDC）的协作感知方法性能进行了比较.结果表明改进SFLA算法性能优于传统SFLA；基于改进SFLA的协作感知方法比MDC方法能获得更大的检测概率，验证

... 相关研究表明^[15]增加青蛙群体多样性和扰动性能够使得算法进一步深度搜索,提高发现最优解概率,本文在此基础上提出了自适应权重因子和双模子族群策略 ...

2009

0.0

. 2009, 37(5):1070-1081 DOI:doi:10.3321/j.issn:0372-2112.2009.05.028

Theory and research progress compressed sensing

压缩感知理论及其研究进展

Shi Guang-ming , Liu Dan-hua , Gao Da-hua

石光明, 刘丹华, 高大化

Sampling is the bridge between analog source signal and digital signal.With the rapid progress of information technologies,the demands for information are increasing dramatically.So the existing systems are very difficult to meet the challenges of high speed sampling,large volume data transmission and storage.How to acquire information in signal efficiently is an urgent problem in electronic information fields.In recent years,an emerging theory of signal acquirement——compressed sensing (CS) provides a golden opportunity for solving this problem.This paper reviews the theoretical framework and the key technical problems of compressed sensing and introduces the latest developments of signal sparse representation,design of measurement matrix and reconstruction algorithm.Then this paper also reviews several open problems in CS theory and discusses the existing difficult problems.In the end,the application fields of compressed sensing are introduced.

信号采样是联系模拟信源和数字信息的桥梁.人们对信息的巨量需求造成了信号采样、传输和存储的巨大压力.如何缓解这种压力又能有效提取承载在信号中的有用信息是信号与信息处理中急需解决的问题之一.近年国际上出现的压缩感知理论(Compressed Sensing,CS)为缓解这些压力提供了解决方法.本文综述了CS理论框架及关键技术问题,并着重介绍了信号稀疏变换、观测矩阵设计和重构算法三个方面的最新进展,评述了其中的公开问题,对研究中现存的难点问题进行了探讨,最后介绍了CS理论的应用领域.

... 1 CS理论CS原理可以描述为^[16]: ...

2012

0.0

. 2012, 34(3):716-721

Wireless sensor networks based on the compressed sensing in multi target locating algorithm

基于压缩感知的无线传感器网络多目标定位算法

He Feng-xing , Yu Zhi-jun , Liu Hai-tao.

何风行, 余志军, 刘海涛

Target localization is one of the most challenging and important issues in Wireless Sensor Networks (WSNs). A multiple target localization method is proposed in WSNs. The multiple target localization issue is transformed into compressed sensing issue by designing iteration backtracking algorithm using multi-resolution analysis idea. The achievement of this algorithm is to save the energy of WSN nodes, by minimizing inter-node communication, in the result of which the lifetime of the WSN is prolonged, at the cost of increasing the computation complexity in the fusion center instead. Emulation results demonstrated that the localization performance is improved by more than 50% by the proposed algorithm.

目标定位是无线传感器网络的重要应用场景。该文提出了一种将压缩感知应用于无线传感器网络多目标定位的方法，把基于网格的多目标定位问题转化为压缩感知问题。应用多分辨率分析的思想，设计了迭代回溯的压缩感知算法，该方法的特点是可同时进行多目标定位，并且大大减少了网络通信的数据量从而延长网络寿命，代价是融合中心的算法复杂度的增加。仿真结果显示，采用迭代回溯算法定位精度提高了以上，具有较好的多目标定位效果。

... CS理论指出当 AM×N满足RIP条件时,通过求解最小 l0范数可以得到稀疏向量 sN×1^[17] ...

2004

0.0

. 2004, 32(5):865-868 DOI:doi:10.3321/j.issn:0372-2112.2004.05.039

Pheromone diffusion method based on ant colony algorithm

基于信息素扩散的蚁群算法

Huang Guo-rui , Cao Xian-bin , Wang Xu-fa.

黄国锐, 曹先彬, 王煦法

Ant Colony Optimization (ACO) Algorithm is a novel search algorithm which simulates the social behavior of ant colony depending on pheromone's communication.Based on the analysis of shortcomings of basic ACO such as lack and lag of collaboration among ants,this paper proposes a new ACO which is more faithful to real ant colony system.By setting up the pheromone diffusion model,this algorithm improves the collaboration among ants which are nearby.The simulation results for TSP problem show the validity of it.

蚁群算法是一种新型的搜索算法,其模拟的是蚁群依赖信息素进行通信而表现出的社会性行为.在基本蚁群算法中,蚂蚁之间协作不足,存在滞后的缺陷.本文在分析这一算法的基础上,提出了一种新的更加忠实了真实蚁群信息系统的蚁群算法.该算法通过建立信息素扩散模型,使相距较近的蚂蚁之间能更好地进行协作.TSP问题的仿真结果表明了该算法的有效性.

... 分别采用DSFLA、PDACO^[18]、文献[3]算法和IDSFLA对TSPLIB中的bayg29、eil51和ch150进行测试 ...