机械结构动态可靠性设计的智能计算方法

引用本文

于繁华, 刘仁云, 张义民, 孙秋成, 张晓丽. 机械结构动态可靠性设计的智能计算方法.吉林大学学报:工学版, 2016, 46(4): 1269-1275
YU Fan-hua, LIU Ren-yun, ZHANG Yi-min, SUN Qiu-cheng, ZHANG Xiao-li. Intelligent algorithm for optimized dynamic reliability design of mechanic structure. Journal of Jilin University Engineering and Technology Edition, 2016, 46(4): 1269-1275 复制到剪切板

Permissions

机械结构动态可靠性设计的智能计算方法

于繁华¹, 刘仁云², 张义民³, 孙秋成², 张晓丽^2,³

1.长春师范大学计算机科学与技术学院,长春 130032

2.长春师范大学数学学院, 长春 130032

3.东北大学机械工程与自动化学院, 沈阳 110004

通讯作者：刘仁云(1968-),女,教授,博士.研究方向:计算智能、结构可靠性设计与优化.E-mail:liurenyun2005@163.com

作者简介:于繁华(1970-),男,教授,博士.研究方向:计算智能及其应用.E-mail:yufanhua@163.com

基金:国家自然科学基金项目(51135003); 吉林省自然科学基金项目(201215149); 吉林省教育厅项目(吉教科合字[2014]第17号,吉教科合[2013]第243号)

摘要

针对多失效模式下机械部件动态可靠性设计问题,提出了一种Monte Carlo-时变极端学习机模型,利用该模型得到了随时间变化的载荷、强度、弹性模量、设计参数等与可靠度的显性函数表示。在此基础上建立了机械部件动态可靠性优化设计模型,并利用所提出的动态粒子群算法对模型进行求解。实验结果表明,该方法能提供整个服役期内满足可靠度要求的所有设计参数,为机械部件动态可靠性优化设计提供了一种行之有效的途径。

关键词: 计算机应用; 极端学习机; 动态粒子群算法; 可靠性优化设计; 多目标优化

中图分类号:TP39,TH12 文献标志码:A 文章编号:1671-5497(2016)04-1269-07

Intelligent algorithm for optimized dynamic reliability design of mechanic structure

YU Fan-hua¹, LIU Ren-yun², ZHANG Yi-min³, SUN Qiu-cheng², ZHANG Xiao-li^2,³

1.College of Computer Science & Technology, Changchun Normal University, Changchun 130032, China

2.College of Mathematics, Changchun Normal University, Changchun 130032, China

3.College of Mechanical Engineering and Automation, Northeastern University, Shenyang 110004, China

Abstract

A Monte Carlo time-varying extreme learning machine is presented for dynamic reliability design of mechanical components under multiple failure modes. The explicit function expression of the reliable degree of these variables, such as the loads, strength, elastic modulus and design parameters, can be obtained by this model. Then, on this basis, a dynamic reliability design model for the mechanical components is established, and the dynamic particle swarm algorithm is applied for the solution of this model. Experiment results show that this method can provide all design parameters meeting the requirement of the reliable degree in the whole service life. This method can be used as an effective approach for optimized dynamic reliability design of mechanical components.

Keyword: computer application; extreme learning machine; dynamic particle swarm algorithm; reliability optimization design; multi-objective optimization

Show Figures

0 引言

传统机械结构的可靠性设计是在静态力学理论基础上建立起来的, 随着时间的推移, 系统受到各种不确定因素的影响, 自身的材料性能、工作环境、载荷和振动效应等都在不断变化, 其可靠度和失效率是随时间动态变化的。如果继续用机械结构设计的初始状态来研究系统服役期的工作状态, 不可能对系统的安全性、可靠性有准确的把握, 有时甚至会造成极大的损失。因此, 对机械结构系统进行动态可靠性设计方法的研究具有很高的实际应用价值^[1]。

近年来, 研究人员运用随机过程和顺序统计理论建立了机械零件强度、载荷和可靠度随时间变化的概率模型, 为动态可靠性研究提供了良好的基础^{[2, 3, 4]}。在实际工程中机械结构往往存在多个失效模式, 并且各个失效模式间存在相关性, 这给多失效模式下机械结构的系统可靠度计算带来一定的困难。为解决这个问题, 学者们提出了将系统失效视为各个失效模式串联的可靠度计算和基于主次失效模式的可靠度计算, 基于二阶联合概率的窄界限理论计算结构可靠度的估计区间等方法^{[5, 6, 7]}。上述研究理论推导严谨, 但均未给出系统可靠度与结构随机参数间的显性表达。文献[8, 9]提出了利用神经网络进行多失效模式下系统可靠度计算, 并给出了结构设计参数与系统可靠度之间的显性函数关系, 在此基础上进行结构系统可靠性优化设计。该研究成果所给出的是机械结构在静止状态下的可靠度, 不能将该方法直接应用到结构系统动态可靠度计算中。极端学习机(Extreme learning machine, ELM)是Huang等^[10]于2006年提出的一种新颖的单隐层前馈神经网络, 该网络将传统的单隐层前馈神经网络参数训练问题转化为求解线性方程组, 解析求得具有最小范数的最小二乘解作为网络输出权值, 整个训练过程一次完成且无需迭代, 与传统迭代式神经网络相比, 网络训练权值的获取将不依赖所选择的训练算法, 增强了网络的泛化能力, 同时训练速度显著提高。近年来, 国内外学者提出了灰色序列极端学习机、选择遗忘机制的极端学习机、免疫极端学习机, 分别在复杂非线性的时变动力过程仿真和预测、混沌时间序列预测、产品系统可靠性参数区间预测等方面取得了良好的效果^{[11, 12, 13]}。可见, 极端学习机具有在时间域上建立良好映射关系的潜质。众多研究成果表明, 极端学习机模型不仅具有训练时间短、泛化能力强等传统计算智能模型无法比拟的优点, 而且还能给出随时间变化的动态映射关系。这些优势为建立机械零部件动态可靠性智能计算模型提供了有力的保障。如果能够借鉴已有的研究进展, 建立能够在时间域上实现映射的时变极端学习机模型, 给出多失效模式下系统动态可靠度与结构随机参数间的时间函数显性表达, 进而实现动态可靠性分析与设计, 并应用于机械产品设计领域, 这将对机械产品可靠性设计理论的应用与发展起到积极的推动作用。

本文在借鉴已有的研究进展的基础上, 建立了能够在时间域上实现映射的时变极端学习机模型, 给出了多失效模式下系统动态可靠度与结构随机参数间的时间函数显性表示, 进而实现动态可靠性分析与设计, 并将其应用于机械产品设计领域, 这将对机械产品可靠性设计理论的应用与发展起到积极的推动作用。

1 时变极端学习机模型

所给出的时变极端学习机模型相对于传统的极端学习机模型而言, 其输出结果和输出层权值均随时间变化, 该模型可以表示为:

$\begin{matrix} \begin{matrix} o_{k} (t) = W^{T} (t) g (ω_{in} x_{k} + b) (1) \\ k = 1, 2, \dots, N \end{matrix} \end{matrix}$

式中:x_k为输入向量;o_k (t)为网络输出;ω_in 为连接输入层和隐含层的权值;b为隐含层偏置量;W^T (t)为连接隐含层和输出层的权值,g(·)为激活函数, 通常情况下取Sigmoid函数; N为样本数,一般ω_in和b在训练开始随机生成并一直保持不变。可以将式(1)改写成矩阵的形式

$\begin{matrix} HW (t) = O (t) (2) \end{matrix}$

式中:

$\begin{matrix} H = (\begin{matrix} g (ω_{2} x_{1} + b_{1}) & \dots & g (ω_{k} x_{2} + b_{n}) \\ ⋮ & ⋮ \\ g (ω_{2} x_{N} + b_{1}) & \dots & g (ω_{k} x_{N} + b_{n}) \end{matrix}) \end{matrix}$ 为极端学习机隐层输出矩阵; n为隐层单元数量。

求解式(2)可得:

$\begin{matrix} W (t) = H^{+} O (t) (3) \end{matrix}$

式中: $\begin{matrix} H^{+} 为 H \end{matrix}$ 的广义逆矩阵。

极端学习机隐层单元个数需要在训练开始之前确定, 隐层单元个数的多少直接关系到极端学习机的学习能力, 如果单元数过少, 将导致网络不能很好地学习; 如果过多, 将会使网络过度拟合, 使网络的泛化能力退化。

2 机械结构强度和弹性模量随时间变化计算模型

将设计基准期T分为L个相等的时间段(t=0,1,2,…,L),每个时间段记为τ,即τ=T/L,通过统计分析确定时间段τ内载荷最大值所对应的工作应力为σ(S_max),这样剩余强度模型可以表示为:

$\begin{matrix} r (t) = r_{0} - [r_{0} - σ (S_{\max})] {(\frac{t}{T})}^{c} (4) \end{matrix}$

式中: $\begin{matrix} r_{0} 为零部件初始强度; T 为设计寿命时间; c \end{matrix}$ 为材料强度退化指数。

由于材料的弹性模量与材料强度的立方根具有线性关系^[14], 弹性模量随时间变化模型可表示为:

$\begin{matrix} E (t) = ρr {(t)}^{\frac{1}{2}} (5) \end{matrix}$

式中: r₀为零部件初始强度;T为设计寿命时间;c为零部件强度随时间退化的过程, 将式(4)带入式(5)可得:

$\begin{matrix} E (t) = ρ {(r_{0} - [r_{0} - σ (S_{\max})] {(\frac{t}{T})}^{c})}^{\frac{1}{2}} (6) \end{matrix}$

3 基于极端学习机的多失效模式下机械结构系统动态可靠度显性表达

考虑具有 k个失效模式的系统,第i个失效模式的动态功能函数为:

$\begin{matrix} g_{i} (X, t) = g_{i} (x_{1}, x_{2}, \dots, x_{n}, t) (7) \end{matrix}$

系统功能函数为:

$\begin{matrix} g (X, t) = g (x_{1}, x_{2}, \dots, x_{n}, t) (8) \end{matrix}$

将第i个失效模式不发生的事件记为E_i=g_i (X,t)≥0,对于典型的串联系统和并联系统, 系统动态可靠度分别表示为:

$\begin{matrix} \begin{matrix} R = P (g (X, t) \geq 0) = P (E_{1} ⋂ E_{2} ⋂ \dots ⋂ E_{k}) (9) \\ R = P (g (X, t) \geq 0) = P (E_{1} ⋃ E_{2} ⋃ \dots ⋃ E_{k}) (10) \end{matrix} \end{matrix}$

由于式(9)和式(10)均为隐式表达式, 不能直接反映出结构随机参数与系统动态可靠度之间的时间函数关系, 给系统动态可靠性分析和优化设计带来了困难。为实现系统动态可靠度的显性表达, 利用所提出的时变极端学习机模型给出结构随机参数与系统动态可靠度之间的显性函数关系, 具体过程如下:

(1) 将设计基准期分成若干个时间段, 每个时间段在不考虑各失效模式之间相关性的前提下, 以各失效模式的可靠度为约束条件, 利用文献[8]所介绍的约束型粒子群算法求得机械结构在静止状态下初始设计点, 在初始设计点附近均匀取样。

(2)在每个时间段下通过式(4)和式(6)分别计算机械结构的强度和弹性模量, 采集该时间段下的载荷最大值。

(3)利用蒙特卡洛模拟计算每个时间段下的各失效模式可靠度和系统可靠度。

(4)将设计参数、载荷、强度、弹性模量、可靠度等组成时间序列样本对, 并输入到时变极端学习机模型中, 进而得到结构随机参数与系统动态可靠度之间的显性函数关系。

为提高极端学习机所拟合对象的稳定性和泛化性, 需要对输入数据进行标准化处理, 其标准化公式为:

$\begin{matrix} X'_{i} = \frac{X_{i} - X_{\min}}{X_{\max} - X_{\min}} (11) \end{matrix}$

式中: $\begin{matrix} X_{i} 为第 i 个变量的值; X_{\max} 和 X_{\min} 分别为该样本序列的最大值和最小值; X'_{i} \end{matrix}$ 为标准化后的值。

4 基于动态粒子群算法的可靠性优化设计

由于对连续变化时间变量进行了时间段上的划分, 这样就可把每个时间区间上的动态多目标优化近似为静态多目标优化问题。基于此, 在建立机械结构多目标优化模型的基础上, 首先给出能够自动检测环境变化的自检算子, 然后设计一种适合所提出的动态多目标优化模型最优解选择的策略, 再次给出响应环境变化的方法。

4.1 优化模型

机械零部件动态可靠性优化设计需要完成如下工作:①零部件在服役期的任意时间段可靠度都大于给定可靠度; ②给出在每个时间段下零部件费用(体积、质量等)最小的设计参数。基于上述两点, 建立的动态可靠性优化设计模型为:

$\begin{matrix} \begin{matrix} minf (X) \\ s . t . R (X, t) \geq R_{0}, t = 0, 1, 2, \dots, L (12) \end{matrix} \end{matrix}$

式中:f(X)为零部件费用函数或其他性能、参数等函数;R(X,t)为零部件在每个时间段的可靠度,该显性函数表达式通过时变极学习机得到;R₀为零部件的给定可靠度。

在处理约束优化问题时惩罚参数的设置直接影响到优化效果, 如何给出合理的惩罚参数值需要反复试验, 由于文中所给出的可靠度约束条件是随时间变化的, 想要设置合理的惩罚参数就变得更加困难, 借鉴文献[15, 16]方法将约束优化看作一个目标优化问题来处理, 这样就把带约束的动态单目标优化问题转化为动态多目标优化问题, 式(12)就改写为:

$\begin{matrix} \{\begin{matrix} minf (X) \\ m i n f_{2} (X) = R_{0} - R (X, t) \end{matrix} (13) \end{matrix}$

4.2 环境变化的自检算子

动态优化问题的关键是在环境发生改变时, 如何使算法自动跟踪环境的改变而继续寻找新的最优解。对粒子群算法中的个体粒子来说, 环境发生变化后个体粒子所对应的适应度值也会发生相应变化。如果出现前、后代粒子的位置接近而对应适应度值却显著不同, 这基本上可以推断环境发生了变化^[17]。令粒子前、后代适应度值与其所对应距离的比值为:

$\begin{matrix} M_{i} (q) = \frac{F (X_{i} (q)) - F (X_{i} (q - 1))}{S_{i} (q)} (14) \end{matrix}$

式中: q代表粒子迭代数;X_i (q)代表粒子i 在第q代的位置;F(X_i (q))代表粒子i 在第q代位置所对应的适应值;M_i(q)代表粒子i前后代适应度值变化与距离变化的比值:

$\begin{matrix} S_{i} (q) = \sqrt[]{\sum_{d}^{=} (X_{id} (q) - X_{id} {(q - 1))}^{2}} (15) \end{matrix}$

式中: X_id(q)代表粒子i的第d个分量在第q代的位置,C_i (p)代表粒子i前后两代适应度值与距离比值的变化率:

$\begin{matrix} C_{i} (q) = \frac{M_{i} (q)}{M_{i} (q - 1)} (16) \end{matrix}$

当环境没有发生变化时, $\begin{matrix} C_{i} (q) \end{matrix}$ 的值接近1, 若发生变化其值将产生跃变。需要说明的是这里只对约束函数目标进行检测, 如果材料强度、载荷、弹性模量等仅是出现微小的变化, 不足以对可靠度造成太大的影响, 则仍在原有优化环境中搜索最优解。

4.3 最优解选择策略

对于机械部件动态可靠性优化设计而言, 要求所得到的解必须在可行区域内, 所以凡是可行区域内的粒子等级规定为1, Pareto最优粒子的等级为2, 其他粒子的等级为3。基于这种思想, 粒子的排序将按如下规则进行:①若两个粒子的等级不同, 则等级低的胜出; ②若两个粒子都在可行区域内, 则函数适应度值小的粒子胜出; ③若两个粒子都是Pareto最优解, 则任意选择一个胜出; ④若两个粒子的等级都为3, 则约束函数值小的胜出。

4.4 响应环境变化的方法

当环境变化时需要对各种群粒子重新置初始值, 产生初始值的原则是:①由于强度、可靠度、弹性模量等随时间推移会呈现逐渐下降趋势, 最近时间段内所得到的最优解可能是最接近下一个时间段的最优解, 为了加快算法的收敛速度, 在全局极值附近选取50%的粒子作为初始值; ②为加强解的多样性, 使其更好地搜索到全局最优解, 剩下50%粒子将随机产生。

4.5 算法描述

Step1 初始化粒子种群:粒子群位置X、速度V、种群规模m、c1、c2、w的值、给定适应度阈值η 、最大迭代次数T_max。初始化记忆池。

Step2 选择由动态极端学习机得到的每个时间段约束目标函数, 若无, 则Goto Step5。否则, 执行下一步。

Step3 判断环境是否发生变化, 若变化加载记忆池, 否则执行下一步。

Step4 while(适应度值> η & & 迭代次数< T_max)

{计算适应度函数;

按最优解选择策略选取个体极值、全局极值;

更新记忆池;

执行基本粒子群算法公式

v_id(q+1)=W* v_id(q)+C₁* r₁* (p_id(q)-x_id(q))+C₂* r₂* (p_gd(q)-x_id(q)); x_id(q+1)=x_id(q)+v_id(q+1)(这里V_id(q)表示第i个粒子的第d个分量在第q代的速度, x_id(q)表示第i个粒子的第d个分量在第q代的位置, p_id(q)为个体极值, p_gd(q)为全局极值)

}

输出本时间段内的最优解

Goto Step2

Step5 结束

5 数值算例

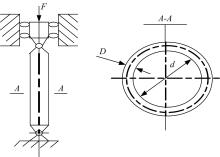
图1为承受轴向载荷的空心压杆计算简图。 F,E,S,ρ,l,d,D分别表示轴向载荷、材料弹性模量、材料屈服极限、材料密度、杆长、截面中径和壁厚。压杆中径d可以在20~140 mm之间选择。壁厚 $\begin{matrix} D \end{matrix}$ 可以在2 mm 与8 mm之间选择。压杆的成本由材料成本和制造成本组成, 即C=5W+2d^1.3,其中,W为压杆质量。材料密度为常量ρ =0.0025 kg/cm², 基本随机参数向量X= [d D F E S l] ^T 。根据统计资料服从I-型极大值分布。其概率密度函数为:

$\begin{matrix} f (x) = θexp [- θ (x - F_{0}) - e^{- θ (x - F_{0})}] (17) \end{matrix}$

式中:分布参数F₀=8.5× 10⁴ N, θ =1.34× 10⁴;E,S均服从正态分布;设计变量d,D为加工尺寸,认为服从正态分布,按一般的制造工艺水平,取变异系数c=0.005。同时考虑空心压杆的两种失效模式——强度失效和刚度失效(失稳),要求系统可靠度大于 $\begin{matrix} _{}_{}_{}_{}_{}_{}^{} R_{s}^{0}_{}_{}^{} \end{matrix}$ (取大于0.92), 求成本比较低的设计方案。

	Figure Option View Download New Window
	图1 空心压杆Fig.1 The hollow rod

(1)定义目标函数

$\begin{matrix} f (X) = C = 5 W + 2 d^{1.3} (18) \end{matrix}$

式中: $\begin{matrix} W = πρdDl, C \end{matrix}$ 为成本。按均值模型求解, 故目标函数为:

$\begin{matrix} E {f (X)} = E (5 W + 2 d^{1, 3}) (19) \end{matrix}$

(2)各失效模式对应的功能函数分别为:

$\begin{matrix} \begin{matrix} g_{1} (X) = S - \frac{F}{πdD} \geq 0 (20) \\ g_{2} (X) = \frac{π^{2} E}{g l^{2}} (d^{2} + D^{2}) - \frac{F}{πdD} \geq 0 (21) \end{matrix} \end{matrix}$

设计规范为:

$\begin{matrix} \begin{matrix} g_{3} (X) = μ_{d} - 10 μ_{D} \geq 0 (22) \\ g_{4} (X) = μ_{d} - 20 \geq 0 (23) \\ g_{5} (X) = 140 - μ_{d} \geq 0 (24) \\ g_{6} (X) = μ_{D} - 2 \geq 0 (25) \\ g_{7} (X) = 8 - μ_{D} \geq 0 (26) \end{matrix} \end{matrix}$

(3)根据简单界限理论, 估计系统可靠度的区间为:

$\begin{matrix} Π_{i = 1}^{k} R_{i} \leq R_{s} \leq R_{\min} \leq R_{i} (27) \end{matrix}$

式中: k为结构的失效模式数,k=2;R_i 为各失效模式的可靠度;R_min为R_i的最小值;R_s为系统的可靠度系统可靠度要满足条件。 $\begin{matrix} _{}_{}_{}_{} R_{s} \geq R_{s}^{0} (R_{s}^{0}_{}_{}^{} \end{matrix}$ 为设计值), 首先需要满足条件 $\begin{matrix} _{}_{}_{}_{}_{}_{}^{}_{}^{} R_{i} \geq R_{s}^{0} 。 \end{matrix}$ 因此, 先不考虑各失效模式之间的相关性, 仅以各失效模式的可靠度作为约束条件, 进行优化设计, 从而得到初始设计点, 如表1所示。

表1 初始设计点 Table 1 Initial design points

各失效模式可靠度 $\begin{matrix} R_{i} \geq R_{s}^{0} (i = 1, 2) \end{matrix}$	d/mm	D/mm
0.92	48.234	2.194
0.95	48.335	2.346
0.990	48.403	2.398

表1 初始设计点 Table 1 Initial design points

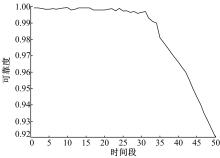
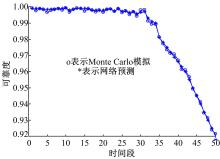
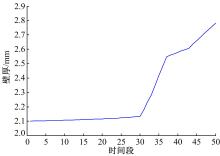
(4)在初始设计点附近的有限邻域内, 对设计变量 $\begin{matrix} X \end{matrix}$ 进行不同水平组合, 结合表1的数据, 使 $\begin{matrix} d, D \end{matrix}$ 分别在区间[47, 50], [2, 3]均匀选取9个数据, 组合得到81个数据。计算每个时间段下的强度、弹性模量以及载荷量, 并与所得到的初始设计数据按正交试验法进行组合, 应用蒙特卡洛模拟进行结构可靠性分析, 选取模拟次数为5000次, 计算得到每个时间段下所对应的可靠度R=[R₁,R₂,R_s ]^T,其中R₁,R₂ 为各失效模式的可靠度,R_s为结构系统可靠度。

(5)将所组成的时间序列样本对输入到时变极端学习机模型中, 得到结构随机参数与系统动态可靠度之间的显性函数关系。图2为在设计参数不变的情况下, 利用时变极端学习机模型得到的机械结构系统可靠度动态变化情况, 图3为Monte Carlo模拟与网络预测结果的比较。这里设计参数取值d=49.243 mm, D=2.265 mm。

	Figure Option View Download New Window
	图2 可靠度随时间变化曲线Fig.2 Reliability curve over time

	Figure Option View Download New Window
	图3 网络预测与Monte Carlo模拟比较Fig.3 Comparison of Network prediction and Monte Carlo

从图2可以看出:机械结构的可靠度随使用时间增加在逐渐降低, 并且中后期较为明显, 这一点实际工程情况一致。从图3可以看出, 所建立时变极端学习机模型能比较精确地实现动态可靠度的预测。

(6)为提高求解精度, 将约束条件(系统动态可靠度)转化为目标函数, 则空心压杆的动态可靠性优化设计模型为:

$\begin{matrix} \{\begin{matrix} \min f_{1} (X) = E [5 W + 2 d^{1, 3}] \\ \min f_{2} (X, t) = R_{s}^{0} - R_{s} (X, t) \\ s . t . g_{i} (X) \geq 0, i = 3, 4, \dots, 7 \end{matrix} (28) \end{matrix}$

式中: $\begin{matrix} R_{s} (t) = HW (t) 。 \end{matrix}$

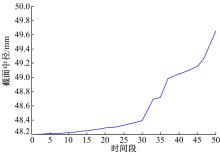
利用动态多目标粒子群算法进行求解, 在实验中在t=0时刻随机产生100个粒子的位置X和速度V,并将随机产生的粒子加入到记忆池,如没有检测到环境变化,输出该时间段的优化结果后继续执行;否则,利用4.4节所介绍的方法响应环境变化。每个时间段内学习因子都为c1=c2=1.2,惯性因子w都从0.8递减到0.1, 最大迭代次数都为150次。图3为截面中径随时间变化的优化尺寸, 图4为壁厚随时间变化的尺寸。

	Figure Option View Download New Window
	图4 截面中径随时间变化的优化尺寸Fig.4 Cross section of size change over time

	Figure Option View Download New Window
	图5 壁厚随时间变化的优化尺寸Fig.5 Wall thickness of size change over time

从图4、图5中可以看出:最优设计尺寸在部件服务初期以及中期都呈现小幅振荡, 并没有发生大的改变, 而到中后期由于零部件强度随时间逐渐减弱, 最优尺寸呈现上升趋势, 以此来保证零部件可靠度要求。

6 结论

(1)建立了能够反映可靠性随时间变化的时变极端学习机模型, 同时将该模型应用于机械部件动态可靠性优化设计。

(2)针对动态约束优化模型求解困难问题, 将动态约束型目标优化问题转换成动态多目标优化问题, 提出了适合该模型求解的动态粒子群算法。

(3)对于机械零部件的动态可靠性优化设计, 只需给出零部件的服役期以及要求达到的可靠度, 便可以通过本文方法找到相应的优化设计尺寸, 提高了零部件的设计水平。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	张义民. 机械动态与渐变可靠性理论与技术评述[J]. 机械工程学报, 2013, 49(20): 101-114. Zhang Yi-min. Review of theory and technology of mechanical reliability for dynamic and gradual systems[J]. Journal of Mechanical Engineering, 2013, 49(20): 101-114. [本文引用:1]
[2]	王新刚, 张义民, 王宝艳. 机械零部件的动态可靠性灵敏度分析[J]. 机械工程学报, 2010, 46(10): 188-193. Wang Xin-gang, Zhang Yi-min, Wang Bao-yan. Dynamic reliability sensitivity analysis of mechanical components[J]. Journal of Mechanical Engineering, 2010, 46(10): 188-193. [本文引用:1]
[3]	王正, 康锐, 谢里阳. 以载荷作用次数为寿命指标的失效相关系统可靠性建模[J]. 机械工程学报, 2010, 46(3): 188-197. Wang Zheng, Kang Rui, Xie Li-yang. Reliability modeling of systems with dependent failure when the Life measured by the number of loadings[J]. Journal of Mechanical Engineering, 2010, 46(3): 188-197. [本文引用:1]
[4]	Fang Yong-feng, Chen Jian-ju. Analysis of structure dynamic reliability under the together stochastic loads[J]. Advances in Information and Science Technology, 2012, 4(8): 74-83. [本文引用:1]
[5]	卢昊, 张义民, 赵长龙, 等. 多失效模式机械零件可靠性灵敏度估计[J]. 机械工程学报, 2012, 48(2): 63-67. Lu Hao, Zhang Yi-min, Zhao Chang-long, et al. Reliability sensitivity estimation of mechanical components with multiple failure modes[J]. Journal of Mechanical Engineering, , 2012, 48(2): 63-67. [本文引用:1]
[6]	喻天翔, 宋笔锋, 万方义, 等. 机械零件多失效模式相关可靠度算法研究[J]. 机械强度, 2006, 28(4): 508-511. Yu Tian-xiang Song Bi-feng Wan Fang-yi. Research on calculating the reliability of mechanical component with correlaed failure modes[J]. Journal of Mechanical Strength, 2006, 28(4): 508-511. [本文引用:1]
[7]	Ditlevsen O. Narrow reliability bounds for structural systems[J]. Mech Based Des Struc, 1979, 7(4): 453-472. [本文引用:1]
[8]	张义民, 刘仁云, 于繁华. 基于计算智能技术的结构系统可靠性优化设计[J]. 工程力学, 2007, 24(8): 27-31. Zhang Yi-min, Liu Ren-yun, Yu Fan-hua. Computational intelligence-based reliability design optimization for structural system[J]. Engineering Mechanics, 2007, 24(8): 27-31. [本文引用:1]
[9]	张义民, 张雷. 结构系统可靠性优化设计的神经网络方法[J]. 计算力学学报, 2005, 22(3): 257-261. Zhang Yi-mi, Zhang Lei. Reliability-based structural optimization using neural network[J]. Chinese Journal of Computational Mechanics, 2005, 22(3): 257-261. [本文引用:1]
[10]	Huang G B, Zhu Q Y. Extreme learning machine: Theory and applications[J]. Neurocomputing, 2006, 70(1): 489-501. [本文引用:1]
[11]	Yin Jian-chuan, Zou Zao-jian, Xu Feng, et al. Online ship roll motion prediction based on grey sequential extreme learning machine[J]. Neurocomputing, 2014, 129(10): 168-174. [本文引用:1]
[12]	张弦, 王宏力. 具有选择与遗忘机制的极端学习机在时间序列预测中的应用[J]. 物理学报, 2011, 60(8): 68-74. Zhang Xian, Wang Hong-li. Selective forgetting extreme learning machine and its application to time series prediction[J]. Acta Phys Sin, 2011, 60(8): 68-74. [本文引用:1]
[13]	林晓华, 冯毅雄, 谭建荣. 基于免疫优化的产品系统可靠性参数区间预测方法[J]. 浙江大学学报: 工学版, 2013, 47(6) : 1013-1021. Lin Xiao-hua, Feng Yi-xiong, Tan Jian-rong. Intervals prediction of system reliability parameters based on immune optimization[J]. Journal of Zhejiang University(Engineering Science), 2013, 47(6) : 1013-1021. [本文引用:1]
[14]	李桂青, 李秋胜. 工程结构时变可靠度理论及其应用[M]. 北京: 科学出版社, 2011: 138-139. [本文引用:1]
[15]	Coello CA. Treating constraintsas objectives for single-objective evolutionary optimization[J] Engineering Optimization, 2000, 32(3): 275-308. [本文引用:1]
[16]	刘若辰, 焦李成, 雷七峰. 一种新的差分进化约束优化算法[J]. 西安电子科技大学学报, 2011, 28(1): 47-53. Liu Ruo-chen, Jiao Li-cheng, Lei Qi-feng. New differential evolution constrained optimization algorithm[J]. Journal of Xidian University, 2011, 28(1): 47-53. [本文引用:1]
[17]	胡静, 曾建潮, 谭瑛. 动态环境下基于种群多样性的微粒群算法[J]. 系统仿真学报, 2007, 19(21): 4932-4935. Hu Jing, Zeng Jian-chao, Tan Ying. Particle swarm optimizer based on diversity of particle in dynamic environments[J]. Journal of System Simulation, 2007, 19(21): 4932-4935. [本文引用:1]

2013

0.0

... 因此,对机械结构系统进行动态可靠性设计方法的研究具有很高的实际应用价值^[1] ...

2010

0.0

. 2010, 46(10):188-193 DOI:doi:10.3901/JME.2010.10.188

Dynamic reliability sensitivity analysis of mechanical components

机械零部件的动态可靠性灵敏度分析

Wang Xin-gang , Zhang Yi-min , Wang Bao-yan.

王新刚, 张义民, 王宝艳

传统的零部件可靠性模型不能很好地反映变幅随机载荷和强度退化对可靠性的影响,忽略可靠度和失效率随使用时间的变化规律.研究机械零件强度、载荷和可靠度随时间的变化规律,运用随机过程和顺序统计理论建立考虑变幅随机载荷和强度退化下机械零件的动态可靠性功能方程模型,利用二阶矩和摄动方法求出机械零部件的动态可靠性指标,并计算出零部件的动态可靠度.以建立的动态可靠性数学模型为基础,将可靠性设计理论与灵敏度分析方法相结合,提出动态可靠性灵敏度设计的计算方法,讨论动态可靠性灵敏度设计问题,以扭杆为例,给出各参数动态可靠性灵敏度的变化规律,分析设计参数的改变对扭杆可靠性的影响,为机械零部件的动态可靠性设计和动态灵敏度设计提供理论依据.

... 近年来,研究人员运用随机过程和顺序统计理论建立了机械零件强度、载荷和可靠度随时间变化的概率模型,为动态可靠性研究提供了良好的基础^[2,3,4] ...

2010

0.0

. 2010, 46(3):188-197 DOI:doi:-

Reliability modeling of systems with dependent failure when the Life measured by the number of loadings

以载荷作用次数为寿命指标的失效相关系统可靠性建模

Wang Zheng , Kang Rui , Xie Li-yang.

王正, 康锐, 谢里阳

摘　要：研究了随机载荷作用次数对齿轮可靠性的影响，通过引入条件可靠度，在不作失效独立假设的前提下，运用应力-强度干涉模型建立了具有多种失效模式的齿轮可靠度计算模型，根据随机载荷作用的统计学意义，运用顺序统计量理论建立了随机载荷多次作用时的齿轮可靠性模型，并研究了齿轮可靠度随载荷作用次数的变化规律，研究表明，即使在强度不退化的情况下，齿轮的可靠度也随着随机载荷作用次数的增加在逐渐降低。

2012

0.0

2012

0.0

. 2012, 48(2):63-67 DOI:doi:10.3901/JME.2012.02.063

Reliability sensitivity estimation of mechanical components with multiple failure modes

多失效模式机械零件可靠性灵敏度估计

Lu Hao , Zhang Yi-min , Zhao Chang-long

卢昊, 张义民, 赵长龙

摘　要：机械零件的失效往往存在多种失效模式,且这些失效模式对可靠性灵敏度均有影响,因此在进行可靠性灵敏度估计时,要充分考虑零件的各个潜在失效模式。提出一种多失效模式机械零件可靠性灵敏度分析的数值方法。运用随机摄动技术和四阶矩技术,求得各失效模式功能函数的前四阶矩及可靠性指标,解决了随机变量分布类型未知时,各失效模式的可靠度计算问题。根据机械零件失效模式较少的特点,将零件的潜在失效模式视为串联关系,则零件整体的失效即为失效模式的串联失效。结合灵敏度分析的梯度算法,推导出关于随机变量均值和方差的可靠性灵敏度的计算公式。数值算例表明所述方法可快速有效地估计多失效模式机械零件的可靠性灵敏度,且适用于非线性功能函数的情况。

... 为解决这个问题,学者们提出了将系统失效视为各个失效模式串联的可靠度计算和基于主次失效模式的可靠度计算,基于二阶联合概率的窄界限理论计算结构可靠度的估计区间等方法^[5,6,7] ...

2006

0.0

. 2006, 28(4):508-511 DOI:doi:10.3321/j.issn:1001-9669.2006.04.008

Research on calculating the reliability of mechanical component with correlaed failure modes

机械零件多失效模式相关可靠度算法研究

喻天翔, 宋笔锋, 万方义

机械零件可靠性在工程设计中具有重要价值,但由于多失效模式间的相关性,使得可靠性设计计算变得很困难.在O.Detlevsen二阶窄界限理论的基础上,提出一种仅考虑主次失效模式相关系数的计算方法,并以一组实际应用中传动轴多失效模式的数据为例,验证所提出的方法.计算结果与Monte Carlo仿真精确计算结果比较接近,表明该算法切实可行,结果完全满足精度要求.

1979

0.0

2007

0.0

. 2007, 24(8):27-31

Computational intelligence-based reliability design optimization for structural system

基于计算智能技术的结构系统可靠性优化设计

Zhang Yi-min , Liu Ren-yun , Yu Fan-hua.

张义民, 刘仁云, 于繁华

... 文献[8,9]提出了利用神经网络进行多失效模式下系统可靠度计算,并给出了结构设计参数与系统可靠度之间的显性函数关系,在此基础上进行结构系统可靠性优化设计 ...

2005

0.0

. 2005, 22(3):257-261 DOI:doi:10.3969/j.issn.1007-4708.2005.03.001

Reliability-based structural optimization using neural network

结构系统可靠性优化设计的神经网络方法

Zhang Yi-mi , Zhang Lei.

张义民, 张雷

In this study two methods are examined. In the first one, the probabilistic perturbation method and the Edgeworth series are employed to give the theoretical formula for reliability-based optimization with non-normal random parameters. Therefore, the probabilistic constraints are transformed into deterministic constraints, and then the reliability-based optimal design parameters could be obtained accurately and quickly. In the second one, neural network (NN) and Monte Carlo simulation (MCS) are applied in reliability-based structural optimization with more failure modes. The neural network is used to simulate the relation expression between the design parameters and the structural reliability based on Monte Carlo simulation. Therefore, the structural probabilistic constraints are transformed into a single equivalent deterministic constraint approximately by NN, and then the process of reliability-based optimization can be implemented conveniently.

针对具有非正态随机参数的可靠性(优化)设计，提出了随机摄动-Edgeworth级数方法，采用该方法将可靠性概率约束转化为等价的确定型约束，可以迅速准确地获得优化设计信息。针对具有多失效模式的结构系统可靠性优化设计，提出了随机模拟一神经网络方法(MCS―NN)，将随机模拟方法与神经网络技术有机结合，为结构系统可靠性优化设计提供了一种新方法。

2006

0.0

... 极端学习机(Extreme learning machine,ELM)是Huang等^[10]于2006年提出的一种新颖的单隐层前馈神经网络,该网络将传统的单隐层前馈神经网络参数训练问题转化为求解线性方程组,解析求得具有最小范数的最小二乘解作为网络输出权值,整个训练过程一次完成且无需迭代,与传统迭代式神经网络相比,网络训练权值的获取将不依赖所选择的训练算法,增强了网络的泛化能力,同时训练速度显著提高 ...

2014

0.0

... 近年来,国内外学者提出了灰色序列极端学习机、选择遗忘机制的极端学习机、免疫极端学习机,分别在复杂非线性的时变动力过程仿真和预测、混沌时间序列预测、产品系统可靠性参数区间预测等方面取得了良好的效果^[11,12,13] ...

2011

0.0

. 2011, 60(8):68-74 DOI:doi:10.7498/aps.60.080504

Selective forgetting extreme learning machine and its application to time series prediction

具有选择与遗忘机制的极端学习机在时间序列预测中的应用

Zhang Xian , Wang Hong-li.

张弦, 王宏力

To solve the problem of extreme learning machine (ELM) on-line training with sequential training samples, a new algorithm called selective forgetting extreme learning machine (SF-ELM) is proposed and applied to chaotic time series prediction. The SF-ELM adopts the latest training sample and weights the old training samples iteratively to insure that the influence of the old training samples is weakened. The output weight of the SF-ELM is determined recursively during on-line training procedure according to its generalization performance. Numerical experiments on chaotic time series on-line prediction indicate that the SF-ELM is an effective on-line training version of ELM. In comparison with on-line sequential extreme learning machine, the SF-ELM has better performance in the sense of computational cost and prediction accuracy.

针对训练样本贯序输入时的极端学习机 (ELM)训练问题,提出一种具有选择与遗忘机制的极端学习机 (SF-ELM),并研究了其在混沌时间序列预测中的应用. SF-ELM以逐次增加新训练样本的方式实现在线训练,通过引入遗忘因子以减弱旧训练样本的影响,同时以泛化能力为判断依据,对其输出权值进行选择性递推更新. 混沌时间序列在线预测实例表明,SF-ELM是一种有效的ELM在线训练模式. 相比于在线贯序极端学习机,SF-ELM具有更快的在线训练速度和更高的在线预测精度,因此更适于混沌时间序列在线预测.

2013

0.0

. 2013, 47(6):1013-1021 DOI:doi:doi:10.3785/j.issn.1008-973X.2013.06.012

Intervals prediction of system reliability parameters based on immune optimization

基于免疫优化的产品系统可靠性参数区间预测方法

Lin Xiao-hua , Feng Yi-xiong , Tan Jian-rong.

林晓华, 冯毅雄, 谭建荣

Aiming at the deficiencies of system reliability prediction, an interval prediction method based on immune optimization algorithm was put forward. First, a prediction neural network of reliability parameters was constructed, which was trained by extreme learning machine (ELM) algorithm. The improved BFGS technique was used to optimize left weights and biases of the network. Then nonlinear regression model was used to construct prediction interval(PI) for reliability parameters based on its point value derived from the trained neural network and the weights of network. So the PI quality depends on the network structure and the weight decay regularizing factor. The immune algorithm was adopted to automate the neural network model selection and adjustment of the weight decay regularizing factor. Model selection and parameter adjustment were carried out through minimization of the PI based cost function called coverage and proportional length based criterion（CPLC）, which combines the coverage probability and the mean interval proportional length of PI. Finally, the proposed theory and method was applied to predict the reliability parameter—mean time between failure(MTBF) of computer numerical control(CNC) lathes, which proved the that prediction performance of the method was better than that of the traditional methods.

针对当前系统可靠性预测方法的不足,提出一种基于免疫优化的区间预测方法.构建可靠性参数预测神经网络模型,由极端学习机（ELM）算法进行训练,并以修正BFGS法对网络的左侧权值和阈值进行调整.在由该网络得到的预测点值和网络权重的基础上,根据非线性回归模型构建可靠性参数的区间预测值（PI）,PI的质量取决于网络结构和权衰减调节参数.结合PI的覆盖率和平均区间比例长度提出一种新的PI综合评价指标,以此衡量PI的质量；引入免疫优化算法优化区间预测值和网络结构,以最小化综合评价指标为成本函数,寻求决策变量，即网络隐层神经元个数和权衰减调节参数的最优值.将提出的方法和理论应用于某系列数控车床的可靠性参数平均无故障时间的预测,证明了其预测性能优于传统方法.

2011

0.0

... 由于材料的弹性模量与材料强度的立方根具有线性关系^[14],弹性模量随时间变化模型可表示为: ...

2000

0.0

2011

0.0

. 2011, 28(1):47-53 DOI:doi:10.3969/j.issn.1001-2400.2011.01.008

New differential evolution constrained optimization algorithm

一种新的差分进化约束优化算法

Liu Ruo-chen , Jiao Li-cheng , Lei Qi-feng.

刘若辰, 焦李成, 雷七峰

摘　要：对于约束优化问题，目前提出的差分进化算法大多采用罚函数法，但此方法对罚参数有很强的依赖性．基于此，把约束优化问题中的约束条件当作一个目标函数，从而把约束优化问题转化为有两个目标函数的多目标优化问题．借鉴多目标优化中的Pareto的概念，对种群中的个体规定等级，便于在优胜劣汰过程中确定选择概率．同时，在算法陷入局部最优时，采用一种不可行解替换机制来提高算法搜索能力．对13个标准测试问题的测试结果表明，与动态惩罚函数的进化算法、可行性规则的差分进化算法、采用随机排序的进化策略以及人工免疫响应约束进化策略相比，新算法在求解精度上均具有一定的优势．

2007

0.0

. 2007, 19(21):4932-4935 DOI:doi:10.3969/j.issn.1004-731X.2007.21.021

Particle swarm optimizer based on diversity of particle in dynamic environments

动态环境下基于种群多样性的微粒群算法

Hu Jing , Zeng Jian-chao , Tan Ying.

胡静, 曾建潮, 谭瑛

针对现有环境检测和环境响应方法存在的不足,提出了改进的基于微粒自身信息的检测方法,不仅降低了的算法复杂度,而且弥补了常用检测方法的局限性.同时还提出了种群多样性和微粒逃逸行为相结合的新型响应方法,将改进的检测和响应方法应用于各种复杂变化的抛物线函数中,结果表明该算法在动态环境中的有效性.

... 如果出现前、后代粒子的位置接近而对应适应度值却显著不同,这基本上可以推断环境发生了变化^[17] ...