混合动力汽车实时优化控制策略仿真分析

引用本文

夏超英, 杜智明. 混合动力汽车实时优化控制策略仿真分析.吉林大学学报:工学版, 2016, 46(4): 1276-1286
XIA Chao-ying, DU Zhi-ming. Simulation analysis on real-time optimal control strategy for hybrid electric vehicle. Journal of Jilin University Engineering and Technology Edition, 2016, 46(4): 1276-1286 复制到剪切板

Permissions

混合动力汽车实时优化控制策略仿真分析

夏超英, 杜智明

天津大学电气与自动化工程学院,天津 300072

通讯作者：杜智明(1983-),男,博士研究生.研究方向:混合动力汽车控制及仿真.E-mail:duzhiming1983@126.com

作者简介:夏超英(1958-),男,教授,博士生导师.研究方向:自动控制理论,混合动力汽车电机及控制系统.E-mail:xiachaoying@126.com

基金:“863”国家高技术研究发展计划项目(2012AA111203)

摘要

针对无级变速混合动力汽车中发动机工作点与道路工况解耦的运行特点,提出一种基于二次型最优控制理论的实时优化控制策略,该策略在保证动力系统输出量跟踪给定值的同时,通过平滑发动机功率运行曲线,从而间接降低车辆燃油消耗。基于ADVISOR软件的二次开发,建立实时优化控制系统的仿真模型,并在8种不同工况下进行仿真对比,结果表明:本文控制策略不仅使车辆具有良好的动力性能,而且在道路工况未知条件下,能显著降低油耗和排放水平,节油效果与基于庞特里亚金最小值原理(Pontryagin's minimum principle,PMP)的全局最优控制策略相近,仅相差1.05%~4.82%。

关键词: 自动控制技术; 并联混合动力汽车; 实时控制策略; 二次型最优控制

中图分类号:TP273 文献标志码:A 文章编号:1671-5497(2016)04-1276-11

Simulation analysis on real-time optimal control strategy for hybrid electric vehicle

XIA Chao-ying, DU Zhi-ming

School of Electrical Engineering and Automation, Tianjin University, Tianjin 300072, China

Abstract

A quadratic real-time optimal control strategy is proposed in accordance with the decoupling characteristics between engine operating point and drive cycle in Hybrid Electric Vehicle (HEV) using Continuous Variable Transmission (CVT). By smoothing the engine operating curve, the strategy minimizes fuel consumption indirectly while the output of the drive system could track the given trajectory. Based on the second development of ADVISOR software, the simulation model is established for real-time optimal control system. Simulation results show that the proposed strategy not only leads to good driving performance of the vehicle with, but also reduces fuel consumption and emission significantly without and priori knowledge of the drive cycle. Compared with the global optimal control strategy based on Pontryagin's Minimum Principle (PMP) under eight types of drive cycle, the difference of fuel consumption is only about 1.05%~4.82%.

Keyword: automatic control technology; parallel hybrid electric vehicle(HEV); real-time control strategy; quadratic optimal control

Show Figures

0 引言

根据混合动力汽车^{[1, 2]}的拓扑结构选择合适的能量管理策略能够有效降低车辆油耗和排放水平, 各国科研人员近年来在该领域的研究主要分为两类:

(1)基于规则的能量管理策略。如Ehsani等^[3]提出的基于工程经验的规则控制策略, 通过预先设置一组门限参数, 如车速、电池荷电状态(State of charge, SOC)限值、发动机运行曲线等, 实时调整动力系统各部件工作状态, 使发动机在限定的高效区域内运行。因该策略实现简单, 在量产车中得到广泛应用, 缺点是规则的设计和门限参数的设置主要依靠工程经验, 且对道路工况的敏感性高。此后, Kheir等^[4]提出以油耗和排放为目标的模糊逻辑控制策略, Baumann等^[5]提出神经网络与模糊规则相结合的控制策略等。该类策略通过将车速、电池组SOC、需求功率等输入量模糊化, 利用模糊控制器中预先设定的基于“ 专家知识” 的规则, 对动力系统的工作模式和需求功率进行合理分配, 从而提高车辆整体性能。近年来, 为提高策略对工况的适应性及获取更好的燃油经济性, 研究人员又提出了诸如粒子群优化算法^[6]、基因算法^[7]等, 但因控制规则的建立仍主要依靠专家经验, 无法保证燃油经济性最优。

(2)基于优化的能量管理策略。如Rimaux等^[8]提出的基于动态规划(Dynamic programming, DP)的最优控制策略, Stockar等^[9]提出的基于庞特里亚金最小值原理(Pontryagin's minimum principle, PMP)的最优控制策略。该类策略以车辆的燃油消耗费用函数最小为目标, 通过Bellman动态规划理论或庞特里亚金最小值原理, 计算指定工况下满足约束条件的最优解。虽然策略实现了真正意义的最优化, 但在实际使用过程中, 由于未来道路工况难以预知, 且计算复杂, 因而很少用于实时控制, 通常主要用于控制策略的评价或控制规则的提取。

Paganelli等^[10]提出等效燃油消耗最小控制策略, 策略将电机的能量消耗转换为等效的发动机油耗, 将该油耗与发动机的实际油耗之和做为名义油耗, 在某个工况瞬时, 从保证系统的名义油耗最小出发, 确定电机的工作点, 实现对发动机、电机输出转矩的优化控制。由于策略中等效因子的取值对道路工况敏感性高, 近年来, 研究人员又提出了诸如神经自适应网络^[11]、在线工况预测^[12]等方法, 根据不同工况对等效因子进行动态修正。该类策略虽然在运算的每个步长内是最优的, 但却无法保证在整个运行区间内最优。

本文针对无级变速混合动力汽车, 提出一种新的能量管理策略。该策略基于二次型最优控制理论, 在保证车辆驾驶性能的基础上, 通过实时优化功率分配, 达到降低整车油耗的控制目标。使用ADVISOR软件在Matlab/Simulink环境下进行仿真模型的二次开发, 通过车辆动力性、节油效果的对比分析, 验证了本文控制策略的有效性。

1 车辆数学模型

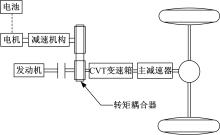
选择无级变速混合动力汽车作为研究对象, 其动力系统拓扑结构如图1所示, 各动力源和变速箱之间通过转矩耦合器连接, 在转矩耦合器的输入侧, 电机的输出轴通过固定减速机构与之相连, 而发动机的输出轴通过离合器与之相连, 通过离合器的投切, 确保发动机按控制策略需求进行启停控制。转矩耦合器输出侧经无级变速箱(Continuously variable transmission, CVT)和主减速器与车轮相连。

	Figure Option View Download New Window
	图1 并联混合动力系统结构示意图Fig.1 Structure diagram of parallel HEV

车辆在行驶过程中受到空气阻力F_ad、滚动阻力F_rr和牵引力F的作用, 其动力学方程为:

$\begin{matrix} M \frac{dv (t)}{dt} + F_{ad} (t) + F_{rr} (t) = F (t) (1) \end{matrix}$

式中:M为汽车总质量; v(t)为车速。

在式(1)的两侧同时乘以车速v(t), 可得车辆功率平衡方程为:

$\begin{matrix} \begin{matrix} \frac{1}{2} M \frac{d v^{2} (t)}{dt} + F_{ad} (t) v (t) + F_{rr} (t) v (t) = \\ P_{ice} (t) + P_{ess} (t) (2) \end{matrix} \end{matrix}$

式中:P_ice(t)为发动机输出功率; P_ess(t)为电机系统输出功率。

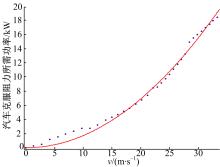
本文提出的实时优化控制策略基于二次型最优控制理论, 其分析对象应是线性系统, 对式(2)所示的非线性微分方程进行线性化处理, 如图2所示, 通过曲线拟合可知空气阻力F_ad(t)和滚动阻力F_rr(t)消耗的功率与车速v(t)的平方近似成正比, 功率平衡方程可线性化为:

$\begin{matrix} \frac{1}{2} M \frac{d v^{2} (t)}{dt} + f v^{2} (t) = P_{ice} (t) + P_{ess} (t) (3) \end{matrix}$

式中:f为线性拟合系数。

	Figure Option View Download New Window
	图2 功率平衡方程中非线性部分的拟合曲线Fig.2 Fitting curve of nonlinear term in power balance equation

永磁电机系统具有宽广的调速范围和高效工作区, 可以满足实时控制策略对电机转矩和功率的需求, 其系统效率η _m近似为常值。电机系统输出功率P_ess(t)与电池组输出功率P_bat(t)之间满足以下关系:

$\begin{matrix} \{\begin{matrix} P_{bat} (t) = P_{ess} (t) / η_{m}, P_{ess} (t) \geq 0 (放电状态) \\ P_{bat} (t) = P_{ess} (t) \cdot η_{m}, P_{ess} (t) < 0 (充电状态) \end{matrix} (4) \end{matrix}$

采用内阻模型的动力电池组, 当内部剩余能量能够满足驾驶需求时, 输出功率P_bat(t)可表示为:

$\begin{matrix} P_{bat} (t) = V_{out} (t) I_{out} (t) = V_{oc} I_{out} (t) - R_{int} I_{out}^{2} (t) (5) \end{matrix}$

式中:V_out(t)、I_out(t)分别为电池组输出电压、电流; V_oc为电池组开路电压; R_int为电池组内阻。

通常, 能量管理策略会控制电池组SOC的波动范围(一般为0.6~0.8), 如图3所示, 此时电池组的输出电压和内阻值变化很小, 近似为常值, 则电池组的动态特性可表示为:

$\begin{matrix} \frac{dSOC (t)}{dt} \end{matrix}$ =- $\begin{matrix} \frac{V_{oc} - \sqrt[]{V_{oc}^{2} - 4 R_{int} P_{bat} (t)}}{2 R_{int} Q_{\max}} \end{matrix}$ (6)

式中:Q_max为电池组的最大容量。

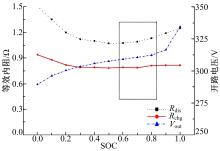	Figure Option View Download New Window
	图3 电池组开路电压和内阻特性图Fig.3 Characteristics of open-circuit-voltage and internal resistance for battery package

当电池组SOC波动范围较小时, 取η _bat为充放电平均效率, 则其动态特性可表示为:

$\begin{matrix} \frac{dSOC (t)}{dt} \cdot E = - \frac{P_{ess} (t)}{η} (7) \end{matrix}$

式中:E为电池组总能量; η 为电池/电机系统的总效率, 满足:

η = $\begin{matrix} \{\begin{matrix} η_{bat} η_{m}, P_{ess} (t) \geq 0 (放电状态) \\ \frac{1}{(} η_{bat} η_{m}), P_{ess} (t) < 0 (充电状态) \end{matrix} \end{matrix}$

若选择x₁(t)=v²(t), x₂(t)=SOC(t)· E为状态量; u₁(t)=P_ice(t), u₂(t)=P_ess(t)为控制量, 由式(3)和式(7)可建立整车动力系统线性化模型为:

$\begin{matrix} \{\begin{matrix} \overset{\cdot}{x} (t) = Ax (t) + Bu (t) \\ y (t) = Cx (t) \end{matrix} (8) \end{matrix}$

式中:x $\begin{matrix} (t) \end{matrix}$ = $\begin{matrix} [\begin{matrix} x_{1} (t) \\ x_{2} (t) \end{matrix}] \end{matrix}$ ; y $\begin{matrix} (t) \end{matrix}$ = $\begin{matrix} [\begin{matrix} y_{1} (t) \\ y_{2} (t) \end{matrix}] \end{matrix}$ ; u $\begin{matrix} (t) \end{matrix}$ = $\begin{matrix} [\begin{matrix} u_{1} (t) \\ u_{2} (t) \end{matrix}] \end{matrix}$ ; A= $\begin{matrix} [\begin{matrix} - \frac{2 f}{M} & 0 \\ 0 & 0 \end{matrix}] \end{matrix}$ ; B= $\begin{matrix} [\begin{matrix} \frac{2}{M} & \frac{2}{M} \\ 0 & - \frac{1}{η} \end{matrix}] \end{matrix}$ ;

C= $\begin{matrix} [\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}] \end{matrix}$ 。

系统在给定的时间区间[t₀, t_f]中, 需要满足以下约束条件:

$\begin{matrix} \{\begin{matrix} lo_soc < SOC (t_{f}) = SOC (t_{0}) < h i_soc \\ 0 \leq P_{ice} (t) \leq P_{ice_\max}, \forall t \in [t_{0}, t_{f}] \\ P_{ess_\min} \leq P_{ess} (t) \leq P_{ess_\max}, \forall t \in [t_{0}, t_{f}] \end{matrix} \end{matrix}$

式中:lo_soc为电池组SOC的最低限值; hi_soc为电池组SOC的最高限值; P_{ice_max}为发动机最大输出功率; P_{ess_min}为电机系统最大制动功率; P_{ess_max}为电机系统最大驱动功率。

2 实时优化控制策略

混合动力汽车能量优化控制的目的是在保证动力系统输出满足驾驶需求的同时, 降低油耗和排放水平, 针对如式(8)所示的车辆模型, 构造如下二次型性能指标:

(1)回收制动模式/电机驱动模式:发动机无动力输出, 由电池/电机系统提供车辆行驶所需的全部功率, 性能指标表示为:

J= $\begin{matrix} \frac{1}{2} \end{matrix} \begin{matrix} \int_{t_{0}}^{t_{f}} \end{matrix}$ [α ₁ $\begin{matrix} (y_{1} (t) - r^{2})^{2} \end{matrix}$ +α ₂ $\begin{matrix} u_{2}^{2} \end{matrix}$ (t)]dt (9)

式中:r为驾驶员的期望车速; 调整权重系数α ₁可实现对车辆驾驶性能的控制; 调整权重系数α ₂可实现对电机系统输出功率的控制。

(2)混合驱动模式:发动机启动工作, 电池组作为能量缓冲器, 避免发动机输出功率因工况变化而大幅波动, 性能指标表示为:

$\begin{matrix} \begin{matrix} J = \frac{1}{2} \int_{t_{0}}^{t_{f}} β_{1} (y_{1} (t) - r^{2})^{2} + β_{2} (y_{2} (t) - x_{2 e})^{2} + \\ β_{3} u_{1}^{2} (t) + β_{4} u_{2}^{2} (t)] dt (10) \end{matrix} \end{matrix}$

式中:x_2e为电池剩余能量; 调整权重系数β ₁可实现对车辆驾驶性能的控制; 调整权重系数β ₂可实现电池剩余能量相对于期望值波动的控制; 调整权重系数β ₃可实现对发动机输出功率的控制; 调整权重系数β ₄可实现对电机系统输出功率的控制。

以混合驱动模式为例, 式(10)所示性能指标可表示成一个二次型跟踪问题, 即:

$\begin{matrix} J = \frac{1}{2} \int_{t_{0}}^{t_{f}} e^{T} (t) Qe (t) + u^{T} (t) Ru (t)) dt (11) \end{matrix}$

式中:e(t)= $\begin{matrix} [\begin{matrix} e_{1} (t) \\ e_{2} (t) \end{matrix}] \end{matrix}$ = $\begin{matrix} [\begin{matrix} r^{2} \\ x_{2 e} \end{matrix}] \end{matrix}$ - $\begin{matrix} [\begin{matrix} y_{1} (t) \\ y_{2} (t) \end{matrix}] \end{matrix}$ 为系统实际输出与期望输出的偏差; z^*= $\begin{matrix} [\begin{matrix} r^{2} \\ x_{2 e} \end{matrix}] \end{matrix}$ 为系统

的期望输出值; Q= $\begin{matrix} [\begin{matrix} β_{1} & 0 \\ 0 & β_{2} \end{matrix}] \end{matrix}$ 和R= $\begin{matrix} [\begin{matrix} β_{3} & 0 \\ 0 & β_{4} \end{matrix}] \end{matrix}$ 为权重系数矩阵, 且满足Q≥ 0, R> 0。

由线性二次型最优控制理论可知, 当性能指标中的终端时间t_f固定时, 最优输出跟踪问题的控制律为:

$\begin{matrix} u (t) = - R^{- 1} B^{T} [K (t) x (t) - g (t)] (12) \end{matrix}$

当终端时间t_f足够大(但有限)时, K(t)在区间[t₀, t_f]中除去在t_f附近一小段时间外, 均为常值K, 且满足代数黎卡提方程, 即:

KA+A^TK-KBR^-¹B^TK+C^TQC=0

同样, 对于常值给定z^*, g(t)在区间[t₀, t_f]中除去在t_f附近一小段时间外, 均为常值g, 且满足代数方程, 即:

$\begin{matrix} {[A - B R^{- 1} B^{T} K]}^{T} \end{matrix}$ g+C^TQz^*=0

由于A-BR^-¹B^TK为稳定矩阵, 故可逆, 因此有:

g=- $\begin{matrix} {\{{[A - B R^{- 1} B^{T} K]}^{T}\}}^{- 1} \end{matrix}$ C^TQz^*

此时常值指令z^*下的最优控制律为:

$\begin{matrix} u (t) = - R^{- 1} B^{T} [Kx (t) - g] (13) \end{matrix}$

将对称矩阵K和伴随向量g代入式(13), 得到一个反馈控制律为常值的二次型最优控制, 即:

$\begin{matrix} \begin{matrix} u (t) = - R^{- 1} B^{T} Kx (t) - R^{- 1} B^{T} \{[A - \\ B R^{- 1} B^{T} {K]}^{T}}^{- 1} C^{T} Q z^{*} (14) \end{matrix} \end{matrix}$

由式(14)可知, 本文提出的控制策略只与系统的当前状态x(t)以及指令信号z^*有关, 是一种可在工况未知条件下应用的实时优化控制策略。表1为不同运行模式下的权系数和黎卡提方程的解, 在反馈控制律的推导过程中, 使用线性化模型只是为得到实时控制策略, 本文后面仿真中使用的控制对象是式(2)和式(6)所示的非线性对象。

表1 不同运行模式下的权系数和黎卡提方程的解 Table 1 Weight coefficient and solution of riccati algebraic equation in different operation modes

控制模式	回收制动模式	电机驱动模式	混合驱动模式
权系数	Q= $\begin{matrix} [\begin{matrix} 1000 & 0 \\ 0 & 0 \end{matrix}] \end{matrix}$ ; R= $\begin{matrix} [\begin{matrix} 0 & 0 \\ 0 & 5 \times 10^{- 4} \end{matrix}] \end{matrix}$	Q= $\begin{matrix} [\begin{matrix} 1000 & 0 \\ 0 & 0 \end{matrix}] \end{matrix}$ ; R= $\begin{matrix} [\begin{matrix} 0 & 0 \\ 0 & 10^{- 3} \end{matrix}] \end{matrix}$	Q= $\begin{matrix} [\begin{matrix} 1000 & 0 \\ 0 & 5 \times 10^{- 6} \end{matrix}] \end{matrix}$ ;
控制量矩阵	$\begin{matrix} [\begin{matrix} P_{ice} (t) \\ P_{ess} (t) \end{matrix}] \end{matrix}$ = $\begin{matrix} [\begin{matrix} 0 \\ - α_{2}^{- 1} {B^{T}}_{12} (K x_{1} (t) - g) \end{matrix}] \end{matrix}$	$\begin{matrix} [\begin{matrix} P_{ice} (t) \\ P_{ess} (t) \end{matrix}] \end{matrix}$ = $\begin{matrix} [\begin{matrix} 0 \\ - α_{2}^{- 1} {B^{T}}_{12} (K x_{1} (t) - g) \end{matrix}] \end{matrix}$	$\begin{matrix} [\begin{matrix} P_{ice} (t) \\ P_{ess} (t) \end{matrix}] \end{matrix}$ = -R^-¹B^T $\begin{matrix} [Kx (t) - g] \end{matrix}$
黎卡提方程的解	K=449.5132;	K=632.508;	K= $\begin{matrix} [\begin{matrix} 791.9953 & 0.0530 \\ 0.0530 & 1.4014 \times 10^{- 4} \end{matrix}] \end{matrix}$ ;

表1 不同运行模式下的权系数和黎卡提方程的解 Table 1 Weight coefficient and solution of riccati algebraic equation in different operation modes

3 仿真模型

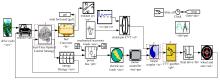
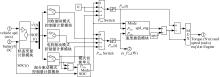
本文提出的实时优化控制策略, 根据动力系统实际输出与期望输出之间的偏差, 直接计算发动机系统和电机系统的控制功率, 为验证控制策略对车辆油耗、尾气排放和电池组SOC的影响, 本文通过ADVISOR软件的二次开发技术, 仅保留原仿真模型中各单元的正向通道, 将软件原有的后向仿真为主、前向仿真为辅的混合仿真方法改为前向仿真方法, 重新搭建的整车仿真模型如图4所示。

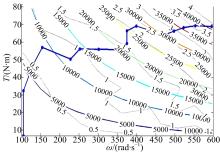
建模思想:在车辆实际行驶过程中, 驾驶员根据道路工况, 通过调节踏板给定指令, 使车辆能够按照给定的工况行驶。在仿真过程中, 为模拟实际驾驶状态, 由道路工况模块(Drive cycle)给出当前时刻的期望车速r(t); 控制策略单元(Real-time optimal control strategy)通过当前实际车速v(t)、期望车速r(t)和电池组SOC实测值SOC(t), 计算发动机控制功率P_ice(t)和电机系统控制功率P_ess(t)。对图1所示的系统, 为使发动机在最优工作曲线(如图5蓝色曲线所示)上运行, 首先控制策略单元根据发动机控制功率P_ice(t), 利用查表插值方法得到发动机最优工作点[spd_eng_opt(t), trq_eng_opt(t)]; 然后由发动机最优转速spd_eng_opt(t)和当前实际车速v(t)确定CVT变速箱的最优速比值cvt_ratio(t); 最后通过电机系统控制功率P_ess(t)及变速箱最优速比确定电机工作点[spd_mc(t), trq_mc(t)], 整个控制过程由发动机节气门、CVT变速箱速比与电机转矩的联调实现。

	Figure Option View Download New Window
	图4 采用实时优化控制策略的ADVISOR仿真模型Fig.4 ADVISOR Simulink model using real-time optimal control strategy

发动机单元(Fuel converter)和电机单元(Motor/controller)在不超过功率限制的前提下, 根据仿真模型前向通道传递过来的转速、转矩需求值, 通过计算分别给出各单元实际能够提供的转速和转矩值。在考虑机械传动效率的前提下, 仿真模型沿系统前向通道依次计算转矩耦合器、CVT变速箱、主减速器等部件实际输出的转速和转矩值, 最终通过汽车车轮模块得到当前时刻的车轮转速, 并将其作为仿真输入回传到整车单元。此时正向通道的仿真计算完成, 仿真模型开始下一时刻的仿真计算。

	Figure Option View Download New Window
	图5 SI-41型发动机燃油消耗MAP图Fig.5 Fuel consumption MAP of SI-41 ICE

根据上述建模思路, 发动机、电机系统忽略瞬态过程, 利用静态MAP效率图建立仿真模型, 电池系统选择内阻模型, 而控制策略单元(图4虚线框1所示)、转矩耦合器单元(图4虚线框2所示)、CVT变速箱单元(图4虚线框3所示)需要重新进行设计, 以下将根据仿真信号传递顺序, 对各单元模型予以详细说明。

3.1 实时优化控制策略单元

图6为实时优化控制策略单元仿真框图。状态变量计算模块将实际车速v(t)和电池组SOC实测值SOC(t)转化为控制量矩阵计算中所需的状态变量x $\begin{matrix} (t) \end{matrix}$ = $\begin{matrix} [\begin{matrix} v^{2} (t) \\ SOC (t) \cdot E \end{matrix}] \end{matrix}$ 。

根据表1给出的控制量矩阵计算公式, 通过回收制动模式控制量计算模块、电机驱动模式控制量计算模块和混合驱动模式控制量计算模块, 得到不同工作模式下的发动机和电机系统控制功率P_ice(t)和P_ess(t), 交由模式切换单元进行模式切换。

模式切换单元以电池组SOC实测值SOC(t)和系统总功率需求P_req(t)=P_ice(t)+P_ess(t)作为输入变量, 确定系统工作模式Mode(t), 具体判定标准为:

(1)回收制动模式(Motor regen):P_req(t)< 0且SOC(t)≤ hi_soc, 此时Mode(t)=1。

(2)电机驱动模式(Motor only):P_req(t)≤ P₀且SOC(t)≥ lo_soc, 此时Mode(t)=2。

(3)混合驱动模式(Engine and motor):除上述两种工作模式外的其他情况, 此时Mode(t)=3。

此外, 为防止系统在不同模式间频繁切换, 模式切换单元还为转换门限设置了一定的滞环宽度。根据系统工作模式Mode(t), 利用选择开关得到当前时刻发动机和电机系统的控制功率P_ice(t)和P_ess(t), 经过限幅, P_ess(t)可直接作为电池组单元(energy storage)的仿真输入, 而P_ice(t)则需通过速度插值模块转化为对应最优工作点的转速、转矩值。

	Figure Option View Download New Window
	图6 实时优化控制策略单元仿真框图Fig.6 Simulink diagram of real-time optimal control strategy block

在混合驱动模式下, 发动机的最优工作曲线以数据表格形式存储在速度插值模块中, 模块根据发动机控制功率P_ice(t), 通过线性插值的方法确定发动机最优工作转速spd_eng_opt(t), 对应的最优工作转矩trq_eng_opt(t)表示为:

$\begin{matrix} trq_eng_opt (t) = \frac{P_{ice} (t)}{spd_eng_opt (t)} (15) \end{matrix}$

在回收制动和电机驱动模式下, 发动机处于怠速状态, 动力输出为零, 此时其最优工作点表示为:

$\begin{matrix} \{\begin{matrix} spd_eng_opt (t) = spd_idle \\ trq_eng_opt (t) = 0 \end{matrix} (16) \end{matrix}$

式中:spd_idle为发动机怠速值。

3.2 转矩耦合器单元

转矩耦合器在发动机、电机和CVT变速箱之间起机械固定和转矩耦合作用, 如图4虚线框2所示, 其输入变量分别为发动机单元和电机单元的实际输出转速、转矩值。

在混合驱动模式下, 转矩耦合器和发动机的实际输出转速相等, 即:

$\begin{matrix} tc_spd_a (t) = spd_eng_a (t) (17) \end{matrix}$

式中:tc_spd_a(t)为转矩耦合器实际输出转速; spd_eng_a(t)为发动机实际输出转速。

在回收制动模式和电机驱动模式下, 发动机不参与工作, 由于电机与转矩耦合器间通过固定减速装置相连, 此时转矩耦合器的实际输出转速表示为:

$\begin{matrix} tc_spd_a (t) = \frac{spd_mc_a (t)}{mc_ratio} (18) \end{matrix}$

式中:spd_mc_a(t)为电机实际输出转速; mc_ratio为固定减速装置的速比。

考虑转矩耦合器的效率因素, 此时转矩耦合器的实际输出转矩tc_trq _a(t)可表示为:

$\begin{matrix} \begin{matrix} tc_trq_a (t) = trq_mc_a (t) * mc_ratio + \\ trq_eng_a (t) - trq_loss (t) \end{matrix} (19) \end{matrix}$

式中:trq_mc_a(t)为电机的实际输出转矩; trq_eng_a(t)为发动机的实际输出转矩; trq_loss(t)为转矩耦合器的损耗。

3.3 CVT变速箱单元

与手动/自动变速箱的换挡过程不同, CVT变速箱要根据控制策略要求, 对速比连续进行调节, 通过与发动机节气门和电机转矩的联调, 确保发动机在需求的最优工作点运行。图4虚线框3所示的CVT变速箱单元(CVT Gearbox)内部主要由两部分组成:

(1)最优速比计算模块:该模块有两个输入变量, 一是变速箱输出侧转速值cvt_spd_out_r(t), 由整车单元根据实际车速v(t), 考虑主减速器的减速比后折算到变速箱输出侧的速度值; 二是变速箱输入侧最优转速值cvt_spd_in_r(t), 由控制策略单元中的速度插值模块计算而得。

混合驱动模式下(见图1), CVT变速箱与发动机之间无减速装置, 因此变速箱输入侧的最优转速值与发动机的最优工作转速spd_eng_opt(t)相同, 即:

$\begin{matrix} cvt_spd_in_r (t) = spd_eng_opt (t) (20) \end{matrix}$

在回收制动和电机驱动模式下, 发动机不参与工作, 为保证系统能在不同工作模式间平稳切换, 使变速箱速比不发生突变, 仿真模型使电机运行在等效最佳工作曲线上。控制策略单元通过线性插值的方法确定电机最优工作转速spd_mc_opt(t), 如图1所示, CVT变速箱与电机之间通过固定减速装置相连, 因此变速箱输入侧的最优转速值可表示为:

$\begin{matrix} cvt_spd_in_r (t) = \frac{spd_mc_opt (t)}{mc_ratio} (21) \end{matrix}$

式中:mc_ratio为固定减速装置的速比。

综上, 仿真过程中CVT变速箱选择的最优速比可统一表示为:

$\begin{matrix} cvt_ratio (t) = \frac{cvt_spd_in_r (t)}{cvt_spd_out_r (t)} (22) \end{matrix}$

(2)变速箱转矩、转速输出计算模块:忽略金属带传动特性和液压执行机构的动力学特性, CVT变速箱输入与输出之间的特性可表示为:

$\begin{matrix} \{\begin{matrix} cvt_spd_out_a (t) = \frac{cvt_spd_in_a (t)}{cvt_ratio (t)} \\ cvt_trq_out_a (t) = (cvt_trq_in_a (t) * \\ cvt_eff (t) - T_{inertia} (t)) * cvt_ratio (t) \end{matrix} (23) \end{matrix}$

式中:cvt_spd_in_a(t)和cvt_trq_in_a(t)分别为变速箱输入侧的实际转速、转矩值; cvt_spd_out_a(t)和cvt_trq_out_a(t)分别为变速箱输出侧的实际转速、转矩值; cvt_eff(t)为变速箱的传动效率, 根据输入侧的实际转速、转矩值使用二维查表插值的方法求得; T_inertia(t)为归算到变速箱输入侧的惯性力矩, 表示为:

$\begin{matrix} T_{inertia} (t) = J \frac{d (cvt_spd_in_a (t))}{dt} (24) \end{matrix}$

式中:J为变速箱输入侧的转动惯量。

4 仿真结果分析

仿真车辆的基本参数如下:FC_SI41emis型发动机的排量为1.0 L; 最大功率为41 kW@5700 r/min; 最大转矩为81 N· m@3477 r/min; ESS_NIMH6型电池的额定容量/电压为6 Ah/308 V; MC_PRIUS型电机的最大功率为31 kW; 迎风面积为2.0 m²; 空气阻力系数为0.335; 滚动阻力系数为0.009; 汽车质量为1287 kg。加速性能体现车辆迅速提高行驶速度的能力, 是衡量车辆动力性能的重要指标。加速性能仿真结果如表2所示, 与传统燃油汽车和采用电量平衡型控制策略^[13]相比, 本文提出的实时优化控制策略能够显著提升车辆加速性能, 在0~96.6 km/h的加速时间仅需14.2 s, 与其他两种情况相比, 性能分别提升33.3%和20.2%。

表2 加速性能仿真结果 Table 2 Simulation results of acceleration 单位:s

目前, 世界主要的排放测试行驶工况分为美国行驶工况、欧洲行驶工况和日本行驶工况3类, 其中以美国FTP(Federal test program)为代表的瞬态工况和以欧洲ECE(Economic commission for Europe)为代表的模态工况应用最为广泛, 我国使用的是以欧洲标准工况NEDC为基础的测试工况。

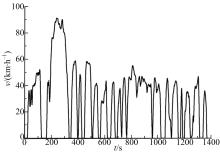
从上述3类测试工况中, 本文选取最具典型意义的8个工况, 其中包括4个美国行驶工况UDDS、FTP、HWFET和CSHVR, 1个欧洲行驶工况NEDC, 日本行驶工况J1015和2个印度行驶工况INDIA_URBAN、INDIA_HWY。图7为美国环境保护署(EPA)制订的UDDS测试工况, 该工况总里程为12 km; 用时1369 s; 平均车速31.51 km/h; 最高车速91.25 km/h, 是美国车辆测试认证的标准工况, 本文以其为例进行仿真对比分析。

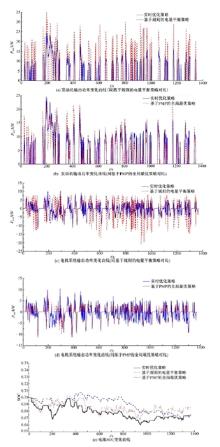
	Figure Option View Download New Window
	图7 UDDS测试工况Fig.7 UDDS driving cycle

设初始状态x₁(t₀)=0, x₂(t₀)=0.7* 6* 308* 3.6 kJ, 在UDDS测试工况条件下, 各控制策略的发动机输出功率、电机系统输出功率和电池组SOC的仿真曲线如图8所示。为验证实时优化控制策略的有效性, 本文将该策略同两类典型控制策略(基于规则的电量平衡型控制策略和基于PMP的全局最优控制策略^[14])进行对比, 研究表明:当电池荷电状态小范围变化时, 协态变量λ 近似为常值, 此时利用PMP方法可以得到全局最优解, 且该计算结果与基于动态规划控制策略得到的节油率基本一致^[14]。

	Figure Option View Download New Window
	图8 UDDS工况下的仿真结果Fig.8 Simulation results under UDDS driving cycle

如图8所示, 3种控制策略在满足车辆驾驶需求的基础上, 均保证了电池组的SOC在期望值附近小幅波动。与基于规则的电量平衡型控制策略相比, 当电池SOC偏离期望值时, 实时优化控制策略能在满足约束要求的前提下, 主动调节发动机和电机系统的输出功率, 并避免发动机功率出现大幅波动, 从而达到节能降耗的目标。与基于PMP的全局最优控制策略相比, 两种策略对发动机输出功率波动情况的控制效果相似, 说明本文的控制策略对油耗指标具有较好的优化效果。

在道路工况未知条件下, 实时优化控制策略同样具有良好的优化效果, 通过8种典型道路工况的仿真对比分析, 如表3所示, 本文的控制策略与全局最优控制策略间的节油率仅相差1.05%~4.82%。

对于火花点燃式发动机, 主要的尾气排放物包括HC、CO和NO_x, 由于发动机的燃油高效区与低排放区并不完全重合, 控制策略通过对发动机运行点的调节, 使其在提高燃油经济性的同时, 不会导致排放水平的显著增加, 这也是判定控制策略有效性的重要标准之一。

表3 不同道路工况油耗仿真结果(L/100 km) Table 3 Fuel consumption results of different driving cycle

表4为8种道路工况条件下, 3种控制策略的排放性能仿真结果, 与电量平衡型控制策略相比, 本文的实时优化控制策略尽管HC的排放水平略有增加, 但燃油消耗降低了1.2%~22%; CO的排放水平降低了28.2%~55.8%; NO_x的排放水平降低了6.5%~20.8%, 因而该策略在减排降耗方面的效果明显优于前者。

表4 不同道路工况排放仿真结果(g/km) Table 4 Emission results of different driving cycle

与全局最优控制策略相比, 实时优化控制策略HC的排放水平增加了1.46%~8.55%; NO_x的排放水平增加了4.14%~22.8%; CO的排放水平则降低了1.8%~33.4%。虽与全局最优控制策略相比, 在减排降耗方面略有差距, 但本文策略计算简便, 对不同工况具有很强的适应性, 更具有工程推广应用的价值。

5 结束语

提出一种基于二次型最优控制理论的实时优化控制策略, 在保证动力系统输出量跟踪给定值的同时, 通过平滑发动机功率运行曲线, 间接达到降低车辆燃油消耗的目的。为了对控制策略的有效性进行验证, 本文选择ADVISOR车辆仿真软件, 通过基于Matlab/Simulink环境的二次开发, 重新搭建满足实时控制策略要求的仿真模型。加速性能仿真以及8种不同道路工况的仿真对比结果表明:该策略不仅使车辆具有良好的动力性能, 而且能显著降低车辆的油耗和尾气排放水平, 作为一种易于工程实现的控制算法, 对指导未来整车能量管理策略的工程开发应用具有重要意义。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Salia A R, Zhang N, Zhu J G. A comparative analysis of fuel economy and emissions between a conventional HEV and the UTS PHEV[J]. IEEE Transactions on Vehicular Technology, 2011, 60(1): 44-54. [本文引用:1]
[2]	Markel T, Simpson A. Plug-in hybrid electric vehicle energy storage system design[C]∥Advanced Automotive Battery Conference, Baltimore, USA, 2006: 1-9. [本文引用:1]
[3]	Ehsani M, Yimin G, Butler K L. Application of electrically peaking hybrid propulsion system to a full-size passenger car with simulated design verification[J]. IEEE Transactions on Vehicular Technology, 1999, 48(6): 1779-1787. [本文引用:1]
[4]	Kheir N A, Salman M A, Schouten N J. Emissions and fuel economy trade-off for hybrid vehicles using fuzzy logic[J]. Mathematics and Computers in Simulation, 2004, 66(2-3): 155-172. [本文引用:1]
[5]	Baumann B, Rizzoni G, Washington G. Intelligent control of hybrid vehicles using neutral networks and fuzzy logic[C]∥SAE Paper, 981061. [本文引用:1]
[6]	吴晓刚, 王旭东, 孙金磊, 等. ISG型混合动力汽车粒子群优化模糊控制研究[J]. 公路交通科技, 2011, 28(6): 146-152. Wu Xiao-gang, Wang Xu-dong, Sun Jin-lei, et al. Research on particle swarm optimization fuzzy control for ISG hybrid electric vehicle[J]. Journal of Highway and Transportation Research and Development, 2011, 28(6): 146-152. [本文引用:1]
[7]	Zhou M L, Lu D K, Li W M, et al. Optimized fuzzy logic control strategy for parallel hybrid electric vehicle based on genetic algorithm[J]. Applied Mechanics and Materials, 2013, 274: 345-349. [本文引用:1]
[8]	Rimaux S, Delhom M, Combes E. Hybrid vehicle powertrain: modeling and control[C]∥Proceedings of the 16th International Electric Vehicle Symposium, Beijing, China, 1999: 120-135. [本文引用:1]
[9]	Stockar S, Marano V, Rizzoni G, et al. Optimal control for plug-in hybrid electric vehicle applications[C]∥American Control Conference, Baltimore, USA, 2010: 5024-5030. [本文引用:1]
[10]	Paganelli G, Delprat S, Guerra T M, et al. Equivalent consumption minimization strategy for parallel hybrid powertrains[C]∥IEEE 55th Vehicular Technology Conference, Birmingham, USA, 2002: 2076-2081. [本文引用:1]
[11]	Gurkaynak Y, Khaligh A, Emadi A. Neural adapative control strategy for hybrid electric vehicles with parallel powertrain[C]∥IEEE Vehicle Power and Propulsion Conference, Piscataway, USA, 2010: 1-6. [本文引用:1]
[12]	Musardo C, Rizzoni G, Staccia B. A-ECMS: an adapative algorithm for hybrid electric vehicle energy management[C]∥IEEE 44th Conference on Decision and Control, Seville, Spain, 2005: 1816-1823. [本文引用:1]
[13]	曾小华, 王庆年, 李骏, 等. 基于ADVISOR2002混合动力汽车控制策略模块开发[J]. 汽车工程, 2004(26): 394-396, 416. Zeng Xiao-hua, Wang Qing-nian, Li Jun, et al. The development of HEV control strategy module based on ADVISOR2002 software[J]. Automotive Engineering, 2004, 26(4): 394-396, 416. [本文引用:1]
[14]	Namwook K, Sukwon C, Huei P. Optimal control of hybrid electric vehicles based on Pontryagin's minimum principle[J]. IEEE Transactions on Control System Technology, 2011, 19(5): 1279-1287. [本文引用:2]

2011

0.0

... 0 引言根据混合动力汽车^[1,2]的拓扑结构选择合适的能量管理策略能够有效降低车辆油耗和排放水平,各国科研人员近年来在该领域的研究主要分为两类: ...

2006

0.0

1999

0.0

... 如Ehsani等^[3]提出的基于工程经验的规则控制策略,通过预先设置一组门限参数,如车速、电池荷电状态(State of charge,SOC)限值、发动机运行曲线等,实时调整动力系统各部件工作状态,使发动机在限定的高效区域内运行 ...

2004

0.0

... 此后,Kheir等^[4]提出以油耗和排放为目标的模糊逻辑控制策略,Baumann等^[5]提出神经网络与模糊规则相结合的控制策略等 ...

0.0

... 此后,Kheir等^[4]提出以油耗和排放为目标的模糊逻辑控制策略,Baumann等^[5]提出神经网络与模糊规则相结合的控制策略等 ...

2011

0.0

. 2011, 28(6):146-152 DOI:doi:10.3969/j.issn.1002-0268.2011.06.024

Research on particle swarm optimization fuzzy control for ISG hybrid electric vehicle

ISG型混合动力汽车粒子群优化模糊控制研究

Wu Xiao-gang , Wang Xu-dong , Sun Jin-lei

吴晓刚, 王旭东, 孙金磊

In the process of controlling the energy distribution of ISG hybrid vehicle，lower precision and limited adaptive capability were caused by using the traditional fuzzy control strategy. A novel particle swarm optimization fuzzy control strategy was proposed. By using particle swarm algorithm，the membership function was optimized based on the control model built by the traditional fuzzy logic. The fuzzy controller parameters that real-time traced by the optimized membership function with environment and load changing was realized. The simulation result shows that this method is able to reduce the change of battery SOC and improve the fuel economy of hybrid electric system compared with using Insight control strategy and the traditional fuzzy control strategy. The experimental result proves that the battery SOC can be controlled within a reasonable scope with this method.

针对ISG型混合动力汽车能量分配的控制过程,应用传统的模糊控制存在精度不高、自适应能力有限等问题。提出一种粒子群优化模糊控制的方法。在应用传统模糊逻辑建立控制模型基础上,利用粒子群算法对模糊控制中的隶属度函数进行优化,实现了优化的隶属度函数随环境变化以及负载变化实时跟踪模糊控制器的参数变化。仿真结果表明,与Insight控制策略和传统模糊控制策略相比,该方法能够降低电池组SOC变化,同时提高混合动力系统的燃油经济性。试验结果验证使用该方法能够在一定程度上将电池SOC控制在比较合理的范围。

... 近年来,为提高策略对工况的适应性及获取更好的燃油经济性,研究人员又提出了诸如粒子群优化算法^[6]、基因算法^[7]等,但因控制规则的建立仍主要依靠专家经验,无法保证燃油经济性最优 ...

2013

0.0

1999

0.0

... 如Rimaux等^[8]提出的基于动态规划(Dynamic programming,DP)的最优控制策略,Stockar等^[9]提出的基于庞特里亚金最小值原理(Pontryagin's minimum principle,PMP)的最优控制策略 ...

2010

0.0

2002

0.0

... Paganelli等^[10]提出等效燃油消耗最小控制策略,策略将电机的能量消耗转换为等效的发动机油耗,将该油耗与发动机的实际油耗之和做为名义油耗,在某个工况瞬时,从保证系统的名义油耗最小出发,确定电机的工作点,实现对发动机、电机输出转矩的优化控制 ...

2010

0.0

... 由于策略中等效因子的取值对道路工况敏感性高,近年来,研究人员又提出了诸如神经自适应网络^[11]、在线工况预测^[12]等方法,根据不同工况对等效因子进行动态修正 ...

2005

0.0

2004

0.0

... 加速性能仿真结果如表2所示,与传统燃油汽车和采用电量平衡型控制策略^[13]相比,本文提出的实时优化控制策略能够显著提升车辆加速性能,在0~96 ...

2011

0.0

... 为验证实时优化控制策略的有效性,本文将该策略同两类典型控制策略(基于规则的电量平衡型控制策略和基于PMP的全局最优控制策略^[14])进行对比,研究表明:当电池荷电状态小范围变化时,协态变量#cod#x003bb ...

... 近似为常值,此时利用PMP方法可以得到全局最优解,且该计算结果与基于动态规划控制策略得到的节油率基本一致^[14] ...