<em> α</em>和高斯噪声背景下线性极化阵列波达方向和极化参数联合估计的FLOCC-SMN方法

引用本文

石屹然, 赵晓晖, 单泽彪, 石要武. α和高斯噪声背景下线性极化阵列波达方向和极化参数联合估计的FLOCC-SMN方法 .吉林大学学报:工学版, 2016, 46(4): 1297-1303
SHI Yi-ran, ZHAO Xiao-hui, SHAN Ze-biao, SHI Yao-wu. FLOCC-SMN method for DOA polarization parameters estimation of linear polarization array in α and Gaussian noise . Journal of Jilin University Engineering and Technology Edition, 2016, 46(4): 1297-1303 复制到剪切板

Permissions

α和高斯噪声背景下线性极化阵列波达方向和极化参数联合估计的FLOCC-SMN方法

石屹然^1,², 赵晓晖¹, 单泽彪¹, 石要武³

1.吉林大学通信工程学院, 长春 130022

2.长春气象仪器研究所, 长春 130012

3.吉林大学生物与农业工程学院, 长春 130022

通讯作者：赵晓晖(1957-),男,教授,博士生导师.研究方向:自适应信号处理理论与应用.E-mail:xhzhao@jlu.edu.cn

作者简介:石屹然(1984-),男,讲师,在站博士后.研究方向:信号处理.E-mail:shiyiran@jlu.edu.cn

基金:国家自然科学基金项目(61571209)

摘要

针对 α和高斯混合噪声背景下的线性极化阵列波达方向和极化参数估计问题,提出了一种基于分数低阶循环相关的子空间-最小范数方法。该方法针对 α稳定分布过程的特点,利用信号的循环平稳特性,克服了传统的基于二阶矩或高阶累积量无法用于 α噪声背景的缺点,弥补了分数低阶矩对循环平稳干扰信号抑制能力的不足。所采用的子空间-最小范数方法不仅减少了传统MUSIC方法的计算量,而且有效地抑制了分数低阶循环相关函数的估计误差。仿真结果表明,本文算法对 α和高斯混合噪声及循环平稳干扰信号的抑制能力明显优于分数低阶矩方法。

关键词: 通信技术; 极化阵列; 稳定分布; 最小范数; 极化参数; 波达方向

中图分类号:TN911.23 文献标志码:A 文章编号:1671-5497(2016)04-1297-07

FLOCC-SMN method for DOA polarization parameters estimation of linear polarization array in α and Gaussian noise

SHI Yi-ran^1,², ZHAO Xiao-hui¹, SHAN Ze-biao¹, SHI Yao-wu³

1.College of Communication Engineering, Jilin University, Changchun 130022, China

2.Changchun Meteorological Instrument Research Institute, Changchun 130012, China

3.College of Biological and Agricultural Engineering, Jilin University, Changchun 130022, China

Abstract

A fractional lower order cyclic correlation-based subspace minimum norm method was proposed for the joint estimation of Directions-of-arrival (DOA) and polarization parameters of linear polarization array under mixed noise of α and/or Gaussian noise. Considering the characteristics of α stable distribution and using the cycle stationarity of signals, the proposed method overcomes the disadvantages of the traditional second order moment or high order cumulant-based methods, which can not by used under α noise. Using the fractional lower order cyclic correlation method, the proposed method makes up for the lack of cycle stationary disturbance suppression of the traditional fractional lower order moment method. The subspace minimum norm method used in this paper can effectively reduce the computation of the traditional MUSIC method and suppress the estimation error of the fractional lower order cyclic correlation function. Simulation results show that the proposed method is superior to the fractional lower order moment-based method for the suppression of the cycle stationary disturbance and the mixed noise of and Gaussian noise.

Keyword: communications; polarization array; stable distribution; minimum norm; polarization parameter; direction of arrival(DOA)

Show Figures

0 引言

传统的极化阵列波达方向(Direction of arrival, DOA)和极化参数联合估计方法^[1]基本上是基于“ 背景噪声为高斯分布” 这一假设。广义中心极限定理保证了这一假设的合理性和广泛适用性。背景噪声符合高斯分布的假设不仅带来理论分析的方便, 而且可以采用二阶矩和高阶累积量这些行之有效的信号处理工具^{[2, 3]}。然而, 在阵列信号DOA估计的实际应用中发现, 其测量环境中不仅存在着高斯噪声, 而且还大量存在着具有非高斯特性的冲击噪声。研究结果^[4]表明, 这种非高斯冲击噪声可以用特征指数为 $\begin{matrix} α (0 < α \leq 2) \end{matrix}$ 的稳定分布过程(以下简称为 $\begin{matrix} α \end{matrix}$ 噪声)来表征。从信号处理的角度来看, $\begin{matrix} α \end{matrix}$ 稳定分布过程有两个重要特点:① $\begin{matrix} α \end{matrix}$ 稳定分布是唯一一种满足广义中心极限定理的广义高斯分布, 高斯分布是 $\begin{matrix} α \end{matrix}$ 稳定分布中, 当 $\begin{matrix} α = 2 \end{matrix}$ 的一个特例, 因此 $\begin{matrix} α \end{matrix}$ 稳定分布比高斯分布具有更广泛的适用范围^[4]; ② $\begin{matrix} α \end{matrix}$ 稳定分布过程仅存在阶次 $\begin{matrix} p < α < 2 \end{matrix}$ 的分数低阶矩(FLOS)^[5]。当 $\begin{matrix} α < 1 \end{matrix}$ 时, 甚至连均值的运算也不可能。 $\begin{matrix} α \end{matrix}$ 稳定分布过程的这一性质直接导致传统的基于高阶累积量或基于二阶矩的信号处理方法在 $\begin{matrix} α \end{matrix}$ 噪声背景下性能急剧下降。

在自然界中, 由于 $\begin{matrix} α \end{matrix}$ 噪声往往与高斯噪声混杂在一起, 因此, 在阵列信号处理中, 人们更关注的是对 $\begin{matrix} α \end{matrix}$ 噪声和高斯噪声均具有极强抑制能力的高分辨率DOA估计方法研究。由于 $\begin{matrix} α \end{matrix}$ 稳定分布仅存在着 $\begin{matrix} 0 < p < α < 2 \end{matrix}$ 的分数低阶矩, 因此目前 $\begin{matrix} α \end{matrix}$ 噪声背景下的阵列信号DOA估计基本上都是采用FLOS或由其派生的方法处理^[6]。Nikias等^[7]提出了一种基于共变的线性阵列DOA估计鲁棒MUSIC方法, 该方法实现了在 $\begin{matrix} α \end{matrix}$ 噪声背景下, 线性阵列的DOA参数估计, 并取得了较好的实验结果。MUSIC方法仅适于阵列信号和附加噪声为联合 $\begin{matrix} SαS \end{matrix}$ (即标准 $\begin{matrix} α \end{matrix}$ 稳定分布^[8])稳定分布过程情况, 因此具有很大局限性^[9]。针对这一问题, Mendel等^[9]提出了一种基于FLOS的线性阵列DOA估计的鲁棒MUSIC方法, 但该方法仅限于附加噪声为零均值独立同分布(i.i.d) $\begin{matrix} SαS \end{matrix}$ 稳定分布情况, 且要求 $\begin{matrix} α \end{matrix}$ 稳定分布的特征指数为 $\begin{matrix} 1 < α \leq 2, \end{matrix}$ 因此仍具有很大的局限性。

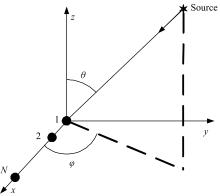
针对上述问题, 本文提出了基于分数低阶循环相关(Fraetional low order cyclic correlation, FLOCC)^[10]的线性极化阵列DOA和极化参数联合估计的子空间-最小范数(Subspace minimum norm, SMN)方法, 该方法可有效抑制任意 $\begin{matrix} α (1 < α \leq 2 \end{matrix}$ )和高斯噪声以及任何异于信号循环频率的平稳干扰信号, 且对分数低阶循环相关函数的估计误差不敏感, 从而大大提高了线性极化阵列DOA和极化参数估计的精度及算法的鲁棒性。

1 线性极化阵列的接收信号模型

以三维坐标系的原点作为相位参考点, 设 N个电磁矢量传感器以阵元间距d沿x轴均匀排列。则线性极化阵列结构如图1所示^[11]。

	Figure Option View Download New Window
	图1 电磁矢量传感器线性极化阵列结构图Fig.1 Structure diagram of linear electromagnetic vector sensor array

设远场空域内有 $\begin{matrix} K \end{matrix}$ 个电磁信号以入射角度为 $\begin{matrix} (θ_{k}, φ_{k}) 、 \end{matrix}$ 极化信息为 $\begin{matrix} (γ_{k}, η_{k}) \end{matrix}$ 入射到图1所示的线性极化阵列, 则极化阵列接收信号可表示为^[11]:

$\begin{matrix} \begin{matrix} X (t) = \overset{K}{\sum_{k = 1}} b_{k} (θ_{k}, φ_{k}) \otimes a_{k} S_{k} (t) + n (t) = \\ AS (t) + n (t) (1) \end{matrix} \end{matrix}$

式中: $\begin{matrix} \otimes \end{matrix}$ 表示Kronectker积; $\begin{matrix} b_{k} (θ_{k}, φ_{k}) = [1, U_{k}, \dots, U_{k}^{N - 1}] \end{matrix}$ 为入射信号的 $\begin{matrix} N \times 1 \end{matrix}$ 维空域导向矢量; 其中 $\begin{matrix} U_{k} = \exp [j 2 πdsin θ_{k} \cos φ_{k}] / λ \end{matrix}$ 为空间相位因子, $\begin{matrix} λ \end{matrix}$ 为入射信号的波长, $\begin{matrix} d \leq λ / 2; A = [b_{1} (θ_{1}, φ_{1}) \otimes a_{1}, b_{2} (θ_{2}, φ_{2}) \otimes a_{2}, \dots, b_{k} (θ_{k}, φ_{k}) \otimes a_{k}] \end{matrix}$ 为 $\begin{matrix} 6 N \times K \end{matrix}$ 维空域-极化域导向矢量阵。其中 $\begin{matrix} 6 \times 1 \end{matrix}$ 维极化— 角度域导向矢量 $\begin{matrix} a_{k} \end{matrix}$ 为:

$\begin{matrix} \begin{matrix} a_{k} = a_{k} (θ_{k}, φ_{k}, γ_{k}, η_{k}) ≜ [\begin{matrix} a_{1 k} \\ a_{2 k} \\ a_{3 k} \\ a_{4 k} \\ a_{5 k} \\ a_{6 k} \end{matrix}] ≜ \\ \underset{Θ_{k}}{\underset{︷}{[\begin{matrix} \cos θ_{k} \cos φ_{k} & - \sin φ_{k} \\ \cos θ_{k} \sin φ_{k} & \cos φ_{k} \\ - \sin θ_{k} & 0 \\ - \sin φ_{k} & - \cos θ_{k} \cos φ_{k} \\ \cos φ_{k} & - \cos θ_{k} \sin φ_{k} \\ 0 & \sin θ_{k} \end{matrix}]}} \underset{g_{k}}{\underset{︷}{[\begin{matrix} \sin γ_{k} e^{j η_{k}} \\ \cos γ_{k} \end{matrix}]}} (2) \end{matrix} \end{matrix}$

式中: $\begin{matrix} S (t) = {[S_{1} (t), S_{2} (t), \dots, S_{k} (t)]}^{T} \end{matrix}$ 为入射信号矢量矩阵; $\begin{matrix} n (t) = [n_{1} (t), n_{2} (t), \dots, n_{k} {(t)]}^{T} \end{matrix}$ 为阵列的附加噪声矢量矩阵。

不失一般性, 这里假设:

(1) $\begin{matrix} {\{S_{k} (t)\}}_{k = 1}^{K} \end{matrix}$ 是 $\begin{matrix} K \end{matrix}$ 个谱密度未知的循环频率相同的零均值循环平稳过程, 且假设循环频率 $\begin{matrix} ω \end{matrix}$ 已知。

(2)加性噪声 $\begin{matrix} n_{i} (t) = n_{αi} (t) + n_{gi} (t), \end{matrix}$ 其中 $\begin{matrix} n_{αi} (t) \end{matrix}$ 为任意零均值 $\begin{matrix} α (0 < α < 2) \end{matrix}$ 噪声, $\begin{matrix} n_{gi} (t) \end{matrix}$ 为高斯有色噪声, 且 $\begin{matrix} n_{αi} (t) 、 n_{gi} (t) \end{matrix}$ 以及各 $\begin{matrix} S_{k} (t) \end{matrix}$ 之间相互统计循环独立。

2 本文方法

定义由式(1)所示的线性极化阵列含噪输出信号矢量的 $\begin{matrix} 6 N \times 6 N \end{matrix}$ 维分数低阶循环相关函数(FLOCC)矩阵为:

$\begin{matrix} R_{X, p}^{ω} = E [X (t + \frac{τ}{2}) {|X^{H} (t - \frac{τ}{2})|}^{(p - 1)} e^{- j 2 πωt}] (3) \end{matrix}$

式中: $\begin{matrix} ω \end{matrix}$ 为循环频率, 假设 $\begin{matrix} ω \end{matrix}$ 是已知的; $\begin{matrix} p \end{matrix}$ 表示分数低阶矩的阶次; 上标H表示共轭转置。根据文献[10], 当 $\begin{matrix} p < α < 2 \end{matrix}$ 时, 该分数低阶循环相关函数矩阵存在。

根据分数低阶循环相关函数性质, 式(3)可写为:

$\begin{matrix} R_{X, p}^{ω} = \overset{K}{\sum_{k = 1}} b (θ_{k}, φ_{k}) \otimes a_{k} r_{S_{k}}^{ω} {[b (θ_{k}, φ_{k}) \otimes a_{k}]}^{H} (4) \end{matrix}$

式中: $\begin{matrix} r_{S_{k}, S_{k}}^{ω} (τ) \end{matrix}$ 为 $\begin{matrix} S_{k} \end{matrix}$ 的分数低阶循环相关函数:

$\begin{matrix} r_{S_{k}, S_{k}}^{ω} (τ) = E [S_{k} (t + \frac{τ}{2}) {|S_{k}^{*} (t - \frac{τ}{2})|}^{(p - 1)} e^{- j 2 πωt}] (5) \end{matrix}$

由式(4)整理可得

$\begin{matrix} R_{X, p}^{ω} = A R_{S, P}^{ω} A^{H} (6) \end{matrix}$

式中: $\begin{matrix} R_{S, P}^{ω} = diag [r_{S_{1}, S_{1}, p}^{ω} (τ), r_{S_{2}, S_{2}, p}^{ω} (τ), \dots, r_{S_{k}, S_{k}, p}^{ω} (τ)]; A \end{matrix}$ 为空域— 极化域导向矢量矩阵:

$\begin{matrix} \begin{matrix} A = \\ [b_{1} (θ_{1}, φ_{1}) \otimes a_{1}, b_{2} (θ_{2}, φ_{2}) \otimes a_{2}, \\ \dots, b_{k} (θ_{k}, φ_{k}) \otimes a_{k}] = \\ [\begin{matrix} a_{1} & a_{2} & \dots & a_{k} \\ U_{1} a_{1} & U_{2} a_{2} & \dots & U_{k} a_{k} \\ ⋮ & ⋮ & ⋮ \\ U_{1}^{N - 1} a_{1} & U_{2}^{N - 1} a_{2} & \dots & U_{k}^{N - 1} a_{k} \end{matrix}] (7) \end{matrix} \end{matrix}$

设空间有K个完全极化循环平稳信号以θ_k,φ_k,γ_k,η_k入射到线性极化阵列, 不难证明, 矩阵 $\begin{matrix} R_{X, p}^{ω} 的秩为 k 。 \end{matrix}$ 对式(7)进行奇异值分解, 得:

$\begin{matrix} R_{X, p}^{ω} = UΣ V^{H} = [\begin{matrix} U_{1} & U_{2} \end{matrix}] [\begin{matrix} Σ_{1} & 0 \\ 0 & 0 \end{matrix}] [\begin{matrix} {V^{H}}_{1} \\ {V^{H}}_{2} \end{matrix}] (8) \end{matrix}$

式中: $\begin{matrix} Σ_{1} = diag [σ_{1}, σ_{2}, \dots, σ_{k}] \end{matrix}$ 为矩阵 $\begin{matrix} R_{X, p}^{ω} \end{matrix}$ 的非零奇异值矩阵。

由式(8)可得:

$\begin{matrix} \begin{matrix} R_{X, p}^{ω} = U_{1} Σ_{1} {V^{H}}_{1} (9) \\ R_{X, p}^{ω} {V^{H}}_{2} = 0 (10) \end{matrix} \end{matrix}$

将式(6)带入式(10), 由于 $\begin{matrix} A \end{matrix}$ 为高矩阵, 且 $\begin{matrix} R_{S, P}^{ω} \end{matrix}$ 可逆, 因而有:

$\begin{matrix} A^{H} V_{2} = 0 (11) \end{matrix}$

这说明信号导向矢量阵 $\begin{matrix} A \end{matrix}$ 与噪声矢量空间 $\begin{matrix} V_{2} \end{matrix}$ 中任一噪声奇异矢量 $\begin{matrix} V_{i} \in V_{2} \end{matrix}$ 均正交。由文献[12], 线性极化阵列信号的二维DOA和极化参数估计的MUSIC算法可表示为:

$\begin{matrix} P_{MUSIC} (θ, φ, γ, η) = \arg \underset{θ, φ, γ, η}{MAX} \frac{1}{{|{V^{H}}_{2} A (θ, φ, γ, η)|}^{2}} (12) \end{matrix}$

然而, 传统MUSIC算法却存在以下几个缺点:

(1)从式(12)可以看出, 在传统MUSIC算法中, 其参数搜索过程需要利用噪声子空间 $\begin{matrix} V_{2} \end{matrix}$ 的全部噪声奇异矢量, 这严重导致了该算法的计算量相对较大, 在极大程度上限制了该算法的推广和发展。

(2)受接收数据长度的限制、干扰信号以及背景噪声的影响, 其FLOCC矩阵 $\begin{matrix} R_{X, p}^{ω} \end{matrix}$ 必定存在误差, 进而导致 $\begin{matrix} V_{2} \end{matrix}$ 中的奇异矢量也存在误差, 这也对传统MUSIC算法的参数估计精度带来极大的影响。

针对上述问题, 本文提出了FLOCC-SMN方法。由于噪声子空间 $\begin{matrix} V_{2} \end{matrix}$ 中的任意奇异矢量均与导向矢量矩阵 $\begin{matrix} A \end{matrix}$ 正交, 这些奇异矢量构成了 $\begin{matrix} V_{2} \end{matrix}$ 子空间的一组完备正交基。因此, 这一正交基底的任意线性组合也与矩阵 $\begin{matrix} A \end{matrix}$ 正交。根据线性代数理论, 最小范数方法对矩阵误差具有良好的抑制能力。因此, 满足式(12)的最小范数解可表示为^[13]:

$\begin{matrix} \min_{w \in F} w^{H} w (13) \end{matrix}$

式中: $\begin{matrix} F = {w : R_{X, p}^{ω} w = 0, \end{matrix}$ 且 $\begin{matrix} w (0) = 1} 。 \end{matrix}$

将特征矢量 $\begin{matrix} w \end{matrix}$ 表示为 $\begin{matrix} V_{2} \end{matrix}$ 子空间的正交基底的线性组合, 即:

$\begin{matrix} w = \overset{6 N}{\sum_{i = k + 1}} α_{i} {V^{H}}_{i} (14) \end{matrix}$

由 $\begin{matrix} V_{i} (i = k + 1, \dots, 6 N) \end{matrix}$ 之间的正交性, 可得:

$\begin{matrix} w^{H} w = \overset{6 N}{\sum_{i = k + 1}} α_{i}^{2} (15) \end{matrix}$

$\begin{matrix} w (0) = 1 \end{matrix}$ 的条件可表达为:

$\begin{matrix} \overset{6 N}{\sum_{i = k + 1}} α_{i} V_{i}^{*} (0) = 1 (16) \end{matrix}$

因而, 在 $\begin{matrix} R_{X, p}^{ω} w = 0 \end{matrix}$ 且 $\begin{matrix} w (0) = 1 \end{matrix}$ 的约束条件下, 求 $\begin{matrix} w^{H} w \end{matrix}$ 极小的问题, 相当于求如下函数的无条件极值问题:

$\begin{matrix} \begin{matrix} f (α_{i}, λ) = \overset{6 N}{\sum_{i = k + 1}} α_{i}^{2} + λ (\overset{6 N}{\sum_{i = k + 1}} α_{i} w (0) - 1) (17) \\ 令 \\ \frac{\partial f}{\partial α_{i}} = 0, i = k + 1, \dots, 6 N (18) \\ 可得 : \\ 2 α_{i} + λ V_{i}^{*} (0) = 0, i = k + 1, \dots, 6 N (19) \end{matrix} \end{matrix}$

将式(19)代入式(14), 可得:

$\begin{matrix} w = β \overset{6 N}{\sum_{i = k + 1}} V_{i}^{*} (0) {V^{H}}_{i} (20) \end{matrix}$

由约束条件 $\begin{matrix} w (0) = 1, \end{matrix}$ 可得:

$\begin{matrix} \begin{matrix} β = {[\overset{6 N}{\sum_{i = k + 1}} {|V_{i} (0)|}^{2}]}^{- 1} (21) \\ 所以 \\ w = \frac{\overset{6 N}{\sum_{i = k + 1}} V_{i}^{*} (0) {V^{H}}_{i}}{\overset{6 N}{\sum_{i = k + 1}} {|V_{i} (0)|}^{2}} (22) \end{matrix} \end{matrix}$

如前文所述, 由信号导向矢量 $\begin{matrix} A \end{matrix}$ 与噪声矢量子空间 $\begin{matrix} V_{2} \end{matrix}$ 的正交性, 特征矢量 $\begin{matrix} w \end{matrix}$ 也必定与导向矢量 $\begin{matrix} A \end{matrix}$ 正交, 即:

$\begin{matrix} A^{H} w = 0 (23) \end{matrix}$

因此, 式(12)可改写为:

$\begin{matrix} \begin{matrix} P (θ, φ, γ, η) = \arg \max_{θ, φ, γ, η} \frac{1}{{|w A^{H} (θ, φ, γ, η)|}^{2}} = \\ \arg \max_{θ, φ, γ, η} \frac{1}{\det [A^{H} (θ, φ, γ, η) w w^{H} A (θ, φ, γ, η)]} = \\ \arg \max_{θ, φ, γ, η} \frac{1}{\det [g^{H} \underset{Z (θ, φ)}{\underset{︷}{Θ^{H} w w^{H} Θ}} g]} (24) \end{matrix} \end{matrix}$

式中:det $\begin{matrix} [\cdot] \end{matrix}$ 为矩阵行列式运算符。

由于矩阵 $\begin{matrix} Z (θ, φ) \end{matrix}$ 与极化参数 $\begin{matrix} (γ, η) \end{matrix}$ 是相互独立的, 当 $\begin{matrix} Z (θ, φ) \end{matrix}$ 奇异时, $\begin{matrix} P (θ, φ, γ, η) \end{matrix}$ 将出现峰值。因此, 入射信号的DOA参数估计可通过下式的二维搜索获得^[14]:

$\begin{matrix} \{\hat{θ}, \hat{φ}\} = \arg \max_{θ, φ} \frac{1}{\det [Z (θ, φ)]} (25) \end{matrix}$

将 $\begin{matrix} \{\hat{θ}, \hat{φ}\} \end{matrix}$ 代入矩阵 $\begin{matrix} Z (θ, φ) \end{matrix}$ , 由式(24), 入射信号的极化参数即可通过再次的二维搜索获得:

$\begin{matrix} \{\hat{γ}, \hat{η}\} = \arg \max_{γ, η} \frac{1}{\det [g^{H} Z (\hat{θ}, \hat{φ}) g]} (26) \end{matrix}$

对比式(24)和式(25)(26)可见, DOA和极化参数的四维搜索计算等效地转变成了两次二维搜索, 这在极大程度上降低了参数搜索的计算量。

3 仿真验证

实验1 考查线性极化阵列DOA和极化参数联合估计FLOCC-SMN方法的参数估计性能及对噪声和干扰的抑制能力。

实验条件:设线性极化阵列的阵元数为8, 间距为 $\begin{matrix} λ / 2 。 \end{matrix}$ 远场空域内有三个等功率且相互独立的窄带QPSK信号 $\begin{matrix} S_{1} 、 S_{2} \end{matrix}$ 和 $\begin{matrix} S_{3} \end{matrix}$ 入射到线性极化阵列上。其中, $\begin{matrix} S_{1} 、 S_{2} \end{matrix}$ 为待测信源, $\begin{matrix} S_{3} \end{matrix}$ 为干扰信号。 $\begin{matrix} S_{1} 、 S_{2} \end{matrix}$ 的载波频率为 $\begin{matrix} f_{0} = 1 MHz, S_{3} \end{matrix}$ 的载波频率为0.95 MHz, 三个信号的入射角度和极化参数分别为: $\begin{matrix} (θ_{1}, φ_{1}, γ_{1}, η_{1}) = (55 °, 65 °, 35 °, 45 °) 、 (θ_{2}, φ_{2}, γ_{2}, η_{2}) = (125 °, 45 °, 70 °, 35 °) 、 (θ_{3}, φ_{3}, γ_{3}, η_{3}) = (45 °, 10 °, 65 °, 70 °) 。 \end{matrix}$ 附加噪声 $\begin{matrix} n_{α} (t) \end{matrix}$ 为 $\begin{matrix} SαS \end{matrix}$ 稳定分布噪声, 它是按文献[15]方法产生, $\begin{matrix} α = 1.6, \end{matrix}$ 其信噪比采用广义信噪比(Generalized signal to noise ratio, GSNR)^[15]定义; $\begin{matrix} n_{g} (t) \end{matrix}$ 为由高斯白噪声通过一个四阶带通滤波器产生的零均值高斯有色噪声, 其信噪比记为 $\begin{matrix} S N_{g} R 。 \end{matrix}$ 噪声与信号, 以及噪声之间均是统计独立的。取混合信噪比 $\begin{matrix} SNR = GSNR + S N_{g} R = 10 dB (GSNR = S N_{g} R \end{matrix}$ ), 信干比SIR=3 dB, 快拍数为1000, 采样频率 $\begin{matrix} f_{c} = 5 f_{0}, \end{matrix}$ 循环频率 $\begin{matrix} ω = f_{0} = 1 MHz 。 \end{matrix}$

实验方法:使用本文方法对入射信号的DOA和极化参数进行估计。

实验结果:图2和图3分别为本文FLOCC-SMN方法的DOA和极化参数估计的一次典型实验结果。

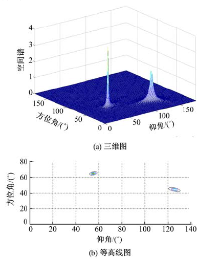	Figure Option View Download New Window
	图2 FLOCC-SMN方法的DOA估计 (SNR=10 dB, SIR=3 dB)Fig.2 DOA estimation of FLOCC-SMN method (SNR=10 dB, SIR=3 dB)

如图2、图3所示, 本文方法可有效地抑制与待测信号循环频率相异的干扰信号(SIR=3 dB)对参数估计带来的影响。并且在 $\begin{matrix} α \end{matrix}$ 稳定分布噪声和高斯有色噪声并存、混合信噪比SNR=10 dB的情况下, 仍然可以以较高精度对待测信号的DOA和极化参数进行估计。

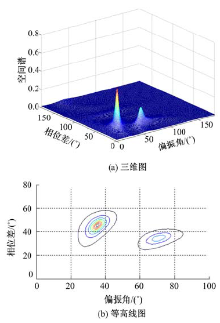实验2 作为比较, 采用与实验1相同的实验条件和实验方法, 但采用基于分数低阶矩( $\begin{matrix} P = 1.4 \end{matrix}$ )的MUSIC方法(FLOC-MUSIC), 图4、图5为待测信号的DOA和极化参数估计一次典型实验结果。

	Figure Option View Download New Window
	图3 FLOCC-SMN方法的极化参数估计(SNR=10 dB, SIR=3 dB)Fig.3 Polarization parameters estimation of FLOCC-SMN method(SNR=10 dB, SIR=3 dB)

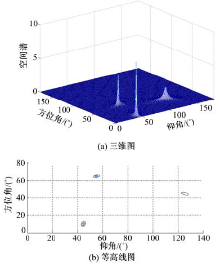	Figure Option View Download New Window
	图4 FLOC-MUSIC方法的DOA估计 (SNR=10 dB, SIR=3 dB)Fig.4 DOA estimation of FLOC-MUSIC method (SNR=10 dB, SIR=3 dB)

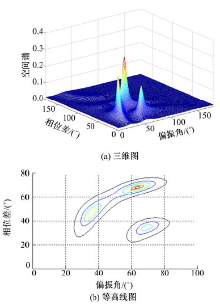	Figure Option View Download New Window
	图5 FLOC-MUSIC方法的极化参数估计 (SNR=10 dB, SIR=3 dB)Fig.5 Polarization parameters estimation of FLOC-MUSIC method(SNR=10 dB, SIR=3 dB)

对比实验1和实验2的仿真结果, 可以明显看出, 在 $\begin{matrix} α \end{matrix}$ 噪声和高斯有色噪声背景下, FLOC-MUSIC方法虽然可以估计出信号的DOA和极化参数, 但是对于循环频率相异的干扰信号 $\begin{matrix} S_{3}, \end{matrix}$ 却出现了明显的伪峰。这说明本文FLOCC-SMN算法对于分离和抑制不同循环频率干扰信号的能力明显优于FLOC-MUSIC算法。

实验3 在不同信噪比条件下, 验证本文FLOCC-SMN方法的参数估计性能。

实验条件:使 $\begin{matrix} α \end{matrix}$ 噪声和高斯有色噪声的混合信噪比(SNR)以5 dB为间隔, 从-10 dB到35 dB变化。其他实验条件与实验1相同。

实验方法:在每种信噪比条件下, 利用本文FLOCC-SMN方法执行100次Monte Carlo实验。并将100次的实验结果进行如下均方根误差(Root mean square error, RMSE)计算:

$\begin{matrix} \begin{matrix} RMS E_{(DOA)} & = \sqrt[]{E [{(\hat{θ} - θ)}^{2} + {(\hat{φ} - φ)}^{2}]} \\ (27) \\ RMS E_{(polarization)} & = \sqrt[]{E [{(\hat{γ} - γ)}^{2} + {(\hat{η} - η)}^{2}]} \\ (28) \end{matrix} \end{matrix}$

式中: $\begin{matrix} \hat{θ} 、 \hat{φ} 、 \hat{γ} 、 \hat{η} \end{matrix}$ 为采用本文FLOCC-SMN方法所得到的DOA和极化参数的估计值;θ、φ、γ、η为参数的真实值。

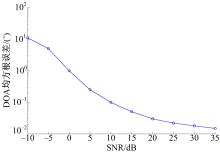
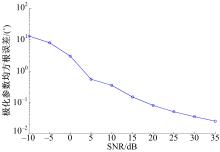
实验结果:图6和图7分别为在不同信噪比条件下, 采用本文FLOCC-SMN方法得到的信号DOA和极化参数估值的RMSE变化曲线。

	Figure Option View Download New Window
	图6 DOA估计的均方根误差曲线Fig.6 RMSE curve of DOA estimation

	Figure Option View Download New Window
	图7 极化参数估计的均方根误差曲线Fig.7 RMSE curve of polarization parameters estimation

由图6和图7可知, 随着 $\begin{matrix} α \end{matrix}$ 噪声和高斯有色噪声的混合信噪比(SNR)的逐渐增加, DOA和极化参数估计的RMSE逐渐减少。而且即使在混合信噪比很低的情况下, 本文FLOCC-SMN方法仍然具有较高的DOA和极化参数估计精度。这充分说明了本文FLOCC-SMN方法能有效地抑制与信号循环不相关的任何有色噪声及干扰。

4 结束语

针对 $\begin{matrix} α \end{matrix}$ 噪声和高斯有色噪声背景下, 线性极化阵列DOA和极化参数估计问题, 提出了一种基于分数低阶循环相关子空间-最小范数方法。首先, 利用信号的循环平稳特性, 采用分数低阶循环相关函数, 不仅克服了基于分数低阶矩类阵列DOA估计方法仅适用于独立同分布(i.i.d) $\begin{matrix} SαS \end{matrix}$ 背景噪声的缺点, 而且还可以充分抑制 $\begin{matrix} α \end{matrix}$ 和高斯混合噪声及与信号循环频率相异的任何循环平稳信号的干扰, 因而具有优良的信号参数估计性能及对各种环境噪声的鲁棒性。其次。针对传统MUSIC方法计算量大的问题, 采用最小范数方法将噪声子空间中的全部奇异矢量等效组合成一个特征矢量, 不仅有效地降低了参数搜索的计算量, 而且还在极大程度上降低了干扰信号以及背景噪声对噪声奇异矢量的误差影响。通过仿真实验, 验证了本文方法可充分抑制与待测信号循环频率相异的任意循环平稳干扰信号, 而且在 $\begin{matrix} α \end{matrix}$ 和高斯噪声混合信噪比较低时, 仍然具有较高的DOA和极化参数估计精度。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	石屹然. 有色噪声背景下极化阵列信号参数估计方法研究[D]. 兰州: 兰州理工大学电气工程与信息工程学院, 2010. Shi Y-iran. Study on methods of parameter estimation of polarization sensitive array signal in colored noise[D]. Lanzhou: College of Electrial and Information Engineering, Lanzhou University of Technology, 2010. [本文引用:1]
[2]	单泽彪, 石要武, 刘小松, 等. 时变遗忘因子动态DOA跟踪算法[J]. 吉林大学学报: 工学版, 2016, 46(2): 632-638. Shan Ze-biao, Shi Yao-wu, Liu Xiao-song, et al. DOA tracking algorithm of moving target with variable forgetting factor[J]. Journal of Jilin University (Engineering and Technology Edition), 2016, 46(2): 632-638. [本文引用:1]
[3]	杨巍, 石要武. 基于分数阶傅里叶变换的宽带Chirp信号的波达方向角估计[J]. 吉林大学学报: 工学版, 2014, 44(3): 818-821. Yang Wei, Shi Yao-wu. Broadband direction-arrival estimation of Chirp signal using fractional Fourier transform[J]. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(3): 818-821. [本文引用:1]
[4]	Shao M, Nikias C L. Signal processing with fractional lower order moments: stable processes and their applications[J]. Proceedings of the IEEE, 1993, 81(7): 986-1010. [本文引用:2]
[5]	Shao M, Nikias C L. Detection and adaptive estimation of stable processes with fractional lower-order moments[C]∥IEEE Sixth SP Workshop on Statistical Signal and Array Processing, Victoria, BC, 1992: 94-97. [本文引用:1]
[6]	何劲. α稳定分布噪声背景下阵列信号处理方法研究[D]. 南京: 南京理工大学电子工程与光电技术学院, 2007. He Jing. Investigation on array signal processing amid α-stable noise[D]. Nanjing: School of Electronic and Optical Engineering, Nanjing University of Science and Technology, 2007. [本文引用:1]
[7]	Tsakalides P, Nikias C L. The robust covariation-based MUSIC (ROC-MUSIC) algorithm for bearing estimation in impulsive noise environments[J]. IEEE Transactions on Signal Processing, 1996, 44(7): 1623-1633. [本文引用:1]
[8]	Samorodnitsky G, Taqqu M S. Stable non-Gaussian rand om processes: stochastic models with infinite variance[J]. Bulletin of the London Mathmatical Society, 1996, 28(134): 554-555. [本文引用:1]
[9]	Liu T H, Mendel J M. A subspace-based direction finding algorithm using fractional lower order statistics[J]. IEEE Transactions on Signal Processing, 2001, 49(8): 1605-1613. [本文引用:2]
[10]	里红杰. 基于分数低阶循环相关的系统辨识及应用研究[D]. 大连: 大连理工大学电子与信息工程学院, 2007. Li Hong-jie. System identification and application based on fractional lower order cyclic correlation[D]. Dalian: School of Electronic and Information Engineering, Dalian University of Technology, 2007. [本文引用:1]
[11]	Wong K T, Zoltowski M D. Closed-form direction-finding with arbitrarily spaced electromagnetic vector-sensors at unknown locations[C]∥Proceedings of the International Conference on Acoustics, Speech, and Signal Processing, Seattle, WA, 1988: 1949-1952. [本文引用:2]
[12]	赵拥军. 宽带阵列信号波达方向估计理论与方法[M]. 北京: 国防工业出版社, 2013. [本文引用:1]
[13]	黄琳. 系统与控制理论中的线性代数[M]. 北京: 科学出版社, 1984. [本文引用:1]
[14]	周欣. 复杂噪声背景下极化阵列信号参数估计的理论与方法研究>. [D]: 长春: 吉林大学通信工程学院, 2009. Zhou Xin. Study on theory and method of signal parameters estimation with polarization sensitive array in complex noise[D]. Changchun: College of Communication Engineering, Jilin University, 2009. [本文引用:1]
[15]	Chambers J M, Mallows C L, Stuck B W. A method for simulating stable rand om variables[J]. Journal of the American Statistical Association, 1976, 71(354): 340-344. [本文引用:1]

2010

0.0

. 2010, :- DOI:doi:10.7666/d.y1712490

Study on methods of parameter estimation of polarization sensitive array signal in colored noise[D]. Lanzhou: College of Electrial and Information Engineering,

有色噪声背景下极化阵列信号参数估计方法研究

Shi Y-iran.

石屹然

电磁矢量传感器阵列信号处理是信号处理领域里的一个新兴的热点研究问题，它在国防、通信、航空等诸多领域都有着广泛的应用前景。　　本文以电磁矢量传感器极化阵列多参数估计为目标，以各种有色噪声抑制为重点，以提高阵列信号参数估计性能为核心，针对各种不同的典型极化阵列结构和信号特性，研究了多种性能优良的阵列信号参数估计方法。首先，对于单电磁矢量传感器DOA和极化参数估计问题，分别研究了基于循环相关和基于高阶累积量的子空间 —最小范数方法；其次，对于工程上应用广泛的线性极化阵列的DOA和极化参数估计问题，又分别研究了基于循环相关...

... 0 引言传统的极化阵列波达方向(Direction of arrival,DOA)和极化参数联合估计方法^[1]基本上是基于#cod#x0201c ...

2016

0.0

.吉林大学学报:工学版, 2016, 46(2):632-638 DOI:doi:10.13229/j.cnki.jdxbgxb201602044

DOA tracking algorithm of moving target with variable forgetting factor

时变遗忘因子动态DOA跟踪算法

Shan Ze-biao , Shi Yao-wu , Liu Xiao-song

单泽彪, 石要武, 刘小松

To track the Direction of Arrival (DOA) of the moving targets quickly and accurately, an adaptive subspace updating algorithm with a variable forgetting factor is proposed. First, this tracking algorithm adaptively adjusts the weights of current and historical data in a covariance matrix according to the DOA change speed. Then the maximum likelihood estimation algorithm is used and the Sequence Quadratic Program (SQP) is applied to optimize the likelihood function in order to reduce the computation cost of the algorithm. Experimental results show that the proposed DOA tracking algorithm has the ability to track coherent sources and obtain acceptable tracking results even under the condition of low SNR and small snapshot number in comparison with other methods.

针对目标信号源波达方向(DOA)实时变化的情况,提出了一种时变遗忘因子的自适应样本协方差矩阵更新方法.时变遗忘因子根据DOA变化的快慢自适应调节自身的大小,从而合理地调整历史数据及当前采样数据在协方差矩阵更新过程中所占的权重.在更新协方差矩阵后,对其直接应用最大似然估计方法,并将序列二次规划(SQP)应用于似然函数的优化求解上,最终实现了DOA的动态跟踪.仿真结果表明:该算法具有解相干的能力和良好的跟踪精度,并且在小样本,低信噪比下仍能达到比较满意的跟踪效果.

... 背景噪声符合高斯分布的假设不仅带来理论分析的方便,而且可以采用二阶矩和高阶累积量这些行之有效的信号处理工具^[2,3] ...

2014

0.0

. 2014, 44(3):818-821 DOI:doi:10.7964/jdxbgxb201403038

Broadband direction-arrival estimation of Chirp signal using fractional Fourier transform

基于分数阶傅里叶变换的宽带Chirp信号的波达方向角估计

Yang Wei , Shi Yao-wu.

杨巍, 石要武

We consider the problem of estimating the Directions of Arrival (DOA) of broadband Chirp signal sources using a sensor array. Since the Fractional Fourier Transform (FRFT) can rotate the time-frequency plane, the frequencies of Chirp signals are concentrated by a properly chosen rotational angle, and the direction array is also obtained in FRFT domain. By this way, the broadband DOAs estimation is then successfully processed using the well existing narrowband DOA estimation algorithms. Simulation results demonstrate that the proposed method is quite simple and has much better performance compared to the methods such as the Coherent Signal Subspace method.

利用分数傅里叶变换(Fractional Fourier transform,FRFT)时频面旋转的特性,将Chirp信号的能量集中,并在分数阶傅里叶域内接收含宽带Chirp信号参数的方向矩阵,然后再通过窄带DOA(Direction of arrival)算法进行波达方向角估计。理论分析和仿真试验证明了该算法的有效性,并且很大程度地提高了信噪比。

... 背景噪声符合高斯分布的假设不仅带来理论分析的方便,而且可以采用二阶矩和高阶累积量这些行之有效的信号处理工具^[2,3] ...

1993

0.0

... 研究结果^[4]表明,这种非高斯冲击噪声可以用特征指数为 α(0α≤2)的稳定分布过程(以下简称为 α噪声)来表征 ...

... 从信号处理的角度来看, α稳定分布过程有两个重要特点:① α稳定分布是唯一一种满足广义中心极限定理的广义高斯分布,高斯分布是 α稳定分布中,当 α=2的一个特例,因此 α稳定分布比高斯分布具有更广泛的适用范围^[4] ...

1992

0.0

... ② α稳定分布过程仅存在阶次 pα2的分数低阶矩(FLOS)^[5] ...

2007

0.0

. 2007, :- DOI:doi:10.7666/d.y1155022

Investigation on array signal processing amid #cod#x003b1;-stable noise

#cod#x003b1;稳定分布噪声背景下阵列信号处理方法研究

He Jing.

何劲

高斯分布噪声在阵列信号处理的方法和应用研究中占据着主导地位。但是，大量的实验数据表明大气噪声、水下声学噪声、电磁干扰噪声等都具有冲击性，因此不适于用高斯分布来描述。近年来，非高斯α稳定分布噪声在信号处理领域受到了广泛的重视，已成为常用的冲击噪声的数学模型。论文根据阵列信号处理的发展，在前人工作的基础上，对非高斯α稳定分布噪声背景下阵列信号处理中的波束形成和波达方向(DOA)估计方法进行了研究，取得了一些有意义的成果。论文内容主要由四部分组成：第一部分背景材料阐述了α稳定分布和阵列信号处理的基本知识。在α稳定分布方面，介绍了单变量和多变量α稳定分布的定义和性质，给出了对称α稳定分布的参数估计方法，以及用于冲击性信号建模的其它常用分布。在阵列信号处理方面，介绍了阵列的基本概念，给出阵列信号处理的数学模型，讨论了阵列信号处理中波束形成和DOA估计的常用方法。第二部分波束形成方法的研究 α稳定分布噪声背景下的波束形成算法基本上都是基于分数低阶统计量展开的。但是，随着噪声冲击强度增大，这类算法的信号干扰噪声比急剧下降，严重地影响了波束形成性能。根据分数低阶统计量和零阶统计量，这部分提出强冲击噪声环境下表现出稳健的波束形成性能的三种新的波束形成算法：分数低阶最小方差无畸变响应波束形成算法(FrMVDR)、线性约束最小几何功率波束形成算法(LCMGP)和最小几何误差波束形成算法(MGPE)。 FrMVDR算法是基于最小方差无畸变响应波束形成算法发展的。类同于传统的阵列响应，首先定义了分数低阶阵列响应；然后，在理论上证明了当分数阶数小于噪声特征指数α的一半时，分数低阶阵列输出功率有界。理论分析和仿真结果表明，基于分数低阶的MVDR算法在任意噪声冲击强度时，都能稳健的工作。FrMVDR算法推广了传统的MVDR算法的应用环境。 LCMGP和MGPE算法都是基于零阶统计量和几何功率发展的。LCMGP算法假设来自期望信号方向的波束响应保持不变，利用波束形成输出几何功率最小化来获取最优权向量。与基于分数低阶矩的波束形成算法相比，LCMGP算法在任意噪声冲击强度时都能稳健的工作，而且LCMGP算法也不需要噪声特征指数的先验信息或估计值。 MGPE算法利用波束形成输出信号和期望信号之间几何功率误差的最小化来求解最优权向量。这类算法的最优权向量没有封闭的表达式，我们采用迭代复加权最小二乘算法对其进行求解。与最小分数低阶误差波束形成算法相比，MGPE算法不需要噪声特征指数的先验信息或估计值，而且可以获得更小的信号估计误差。第三部分DOA估计方法的研究这部分研究了α稳定分布噪声环境下平稳和非平稳信号的DOA估计方法。在平稳信号方面，提出了基于Screened-Ratio原理的MUSIC(SR-MUSIC)算法和基于无穷范数归一化的预处理的MUSIC(IN-MUSIC)算法。在非平稳信号方面，提出了基于FLOM的空-时频域(FLOM-TF-MUSIC)和空-模糊域的MUSIC(FLOM-AD-MUSIC)算法。 SR-MUSIC是根据Screened-Ratio原理构造阵列接收的相关矩阵进行特征分解发展的。该算法不需要FLOM参数p的选择，从而避免了基于阵列共变矩阵(ROC-MUSIC)和阵列FLOM矩阵(FLOM-MUSIC)的DOA估计方法由于需要噪声特征指数的估计和由于不同参数p所带来的DOA估计误差。 IN-MUSIC首先对阵列数据进行无穷范数归一化预处理，然后采用基于二阶统计量的子空间方法进行DOA估计。α稳定分布的噪声不存在有界的二阶矩；但是，经过无穷范数归一化后，我们从理论上证明了归一化的α稳定分布噪声为零均值、有限方差的噪声。因此，无穷范数归一化预处理的阵列信号可以采用子空间分解的方法进行DOA估计。与其它预处理方法相比，无穷范数归一化预处理不需要噪声概率密度函数的信息和人为选择的参数，而且计算也很简单。 FLOM-TF-MUSIC和FLOM-AD-MUSIC都是对非平稳信号提出的。当噪声为冲击噪声时，传统的时频分析方法将不能反映信号的时频二维特性，因此，时频-MUSIC等算法将不再适用。对此，我们在α稳定分布的噪声假设下，引入分数低阶统计量，定义了基于FLOM的时频分布，分析了其性质。然后将基于FLOM的时频分布推广到空域，定义了基于FLOM的空间时频分布矩阵，并对其进行特征分析，发现其结构可用来进行DOA估计。最后结合MUSIC算法实现DOA估计。与时频域相对应，我们还将分数低阶统计量与模糊域分析结合，定义了基于FLOM的模糊函数，并将其推广到空域，定义基于FLOM的空间模糊函数矩阵，分析其特征结构，再利用MUSIC算法实现DOA估计。第四部分：基于矢量传感器阵列的DOA和DOA-极化估计方法研究这部分研究了α稳定分布噪声环境下基于声学矢量阵DOA估计和电磁矢量阵的DOA-极化联合估计方法。首先，对声学矢量阵，提出了一种高斯噪声背景下基于单声学矢量对的二维DOA估计算法(Uni-AUVD-ESPRIT)；对电磁矢量阵，提出了一种高斯噪声背景下的基于单电磁矢量对的二维DOA-极化联合估计算法(Uni-EMVD-ESPRIT)。然后，将这两种算法与FLOM和无穷范数归一化结合，分析了其在α稳定分布噪声中的性能。 Uni-AUVD-ESPRIT算法／Uni-EMVD-ESPRIT算法充分利用空间放置的两个矢量传感器的空间不变性，可获得具有闭式解形式的DOA／DOA-极化参数估计值。算法不需要进行迭代搜索，且适用于任意信号形式。

... 由于 α稳定分布仅存在着 0pα2的分数低阶矩,因此目前 α噪声背景下的阵列信号DOA估计基本上都是采用FLOS或由其派生的方法处理^[6] ...

1996

0.0

... Nikias等^[7]提出了一种基于共变的线性阵列DOA估计鲁棒MUSIC方法,该方法实现了在 α噪声背景下,线性阵列的DOA参数估计,并取得了较好的实验结果 ...

1996

0.0

... MUSIC方法仅适于阵列信号和附加噪声为联合 SαS(即标准 α稳定分布^[8])稳定分布过程情况,因此具有很大局限性^[9] ...

2001

0.0

... MUSIC方法仅适于阵列信号和附加噪声为联合 SαS(即标准 α稳定分布^[8])稳定分布过程情况,因此具有很大局限性^[9] ...

... 针对这一问题,Mendel等^[9]提出了一种基于FLOS的线性阵列DOA估计的鲁棒MUSIC方法,但该方法仅限于附加噪声为零均值独立同分布(i ...

2007

0.0

. 2007, :- DOI:doi:10.7666/d.y1225515

System identification and application based on fractional lower order cyclic correlation[D]. Dalian:School of Electronic and Information Engineering,

基于分数低阶循环相关的系统辨识及应用研究

Li Hong-jie.

里红杰

系统辨识是指根据系统的输入、输出信号及其统计特性进行系统参数的估计。基于循环平稳特性的二阶统计量(SOS)方法与以往基于高阶统计特性(HOS)的方法相比具有计算量小、收敛速度快等优点,因此近年来,基于信号循环平稳特性的系统辨识方法受到了广泛的关注。在传统的信号处理中,高斯信号模型占据主导地位,这种假设在许多情况下是合理的,而且在该模型下设计的信号处理方法易于进行理论上的解析分析。然而,在实际应用中存在的大量非高斯信号和噪声具有显著的尖峰脉冲特性,如水声信号、低频大气噪声及许多人为产生的信号和噪声。如果仍采用高斯分布模型来描述这类过程,将会由于模型与信号噪声不能很好匹配而导致所设计的算法性能显著退化。α稳定分布则为这类过程提供了非常有用的理论工具,因此,通常用α稳定分布来描述这类具有显著尖峰脉冲状波形的随机信号。由于α稳定分布是广义的高斯分布,而高斯分布是α稳定分布的特例,因此α稳定分布模型具有更广泛的适用性。但在分数低阶α稳定分布噪声下,由于没有有限的二阶矩,因此在高斯模型下基于二阶统计量的系统辨识方法不能正常工作。本文首先回顾了系统辨识的发展,然后分别从分数低阶α稳定分布模型和高斯模型这两方面着手,具体介绍了基于共变、α谱的系统辨识方法和基于循环平稳特性的二阶统计量的系统辨识方法。然后结合分数低阶相关和二阶循环相关给出了分数低阶循环相关(FLOCC)的定义,并证明了分数低阶循环相关的循环频率与二阶循环相关的循环频率相等的特性。最后在背景噪声为α稳定分布模型假设条件下,应用分数低阶循环相关理论,依据现有的基于循环平稳特性的二阶统计量的系统辨识方法,给出了基于分数低阶循环相关的系统辨识算法。理论分析和计算机仿真表明,该算法在高斯和非高斯α稳定分布噪声环境下均具有良好的韧性。

... 针对上述问题,本文提出了基于分数低阶循环相关(Fraetional low order cyclic correlation,FLOCC)^[10]的线性极化阵列DOA和极化参数联合估计的子空间-最小范数(Subspace minimum norm,SMN)方法,该方法可有效抑制任意 α(1α≤2)和高斯噪声以及任何异于信号循环频率的平稳干扰信号,且对分数低阶循环相关函数的估计误差不敏感,从而大大提高了线性极化阵列DOA和极化参数估计的精度及算法的鲁棒性 ...

1988

0.0

... 则线性极化阵列结构如图1所示^[11] ...

... 设远场空域内有 K个电磁信号以入射角度为 (θk,φk)、极化信息为 (γk,ηk)入射到图1所示的线性极化阵列,则极化阵列接收信号可表示为^[11]: ...

2013

0.0

1984

0.0

... 因此,满足式(12)的最小范数解可表示为^[13]: ...

2009

0.0

. 2009, :-

Study on theory and method of signal parameters estimation with polarization sensitive array in complex noise

复杂噪声背景下极化阵列信号参数估计的理论与方法研究>.

Zhou Xin.

周欣

由于极化阵列能够同时获取空间电磁信号的空域信息和极化信息而备受学者们的关注。与传统标量传感器阵列相比,极化阵列具有明显的优势:稳健的检测能力、较高的分辨能力、较强的干扰抑制能力以及极化多址能力;当多个极化信号在空间域不能被分辨时,利用信号的极化差异仍然能在极化域被分离;在极化阵列空间孔径较小时,仍然具有较好的分辨率。极化阵列的这些优势使其具有重要的军事、民事应用价值。基于极化阵列的信号多参数估计是极化阵列信号处理的一个重要研究内容,它在雷达、声纳、通信和生物医学等领域有着广泛的应用前景。本文首先介绍了极化阵列信号处理的基础知识,在此基础上,着重讨论了极化阵列信号多参量估计的理论与方法问题。其中包括:复杂噪声背景下循环平稳信号的多参数估计、机载矢量传感器阵列的信号多参数估计、相干信源的多参数估计、α稳定分布噪声背景下极化圆阵信号多参数估计,以及非平稳信号的二维DOA和极化参数估计方法等。这些内容都是极化阵列信号处理领域的研究热点,它们无论对极化阵列信号处理的理论发展还是实际应用,都有重要的意义。

... 因此,入射信号的DOA参数估计可通过下式的二维搜索获得^[14]: ...

1976

0.0

... 6,其信噪比采用广义信噪比(Generalized signal to noise ratio,GSNR)^[15]定义 ...