面向区域的认知无线电系统的频谱感知模型

引用本文

栾磊, 赵晓晖, 徐勇军. 面向区域的认知无线电系统的频谱感知模型.吉林大学学报:工学版, 2016, 46(4): 1304-1312
LUAN Lei, ZHAO Xiao-hui, XU Yong-jun. Region oriented spectrum sensing model for cognitive radio system. Journal of Jilin University Engineering and Technology Edition, 2016, 46(4): 1304-1312 复制到剪切板

Permissions

面向区域的认知无线电系统的频谱感知模型

栾磊^1,², 赵晓晖², 徐勇军²

1.空军大连通信士官学校无线通信系,辽宁大连 116600

2.吉林大学通信工程学院,长春 130012

通讯作者：赵晓晖(1957-),男,教授,博士生导师.研究方向:信号处理.E-mail:xhzhao@jlu.edu.cn

作者简介:栾磊(1983-),男,讲师,博士研究生.研究方向:认知无线电.E-mail:luanleiv126@163.com

基金:国家自然科学基金项目(61171079)

摘要

建立了面向区域的频谱感知模型(RSSM),根据路径损耗和衰落裕度理论推导出了RSSM感知区域的大小。基于RSSM,在单用户频谱感知中分析了阈值设定方法以及次用户位置对频谱感知性能的影响;在协作频谱感知中,利用D-S理论分析了硬决策协作频谱感知中次用户分散性对感知性能的影响。最后通过仿真实验证明了本文模型的正确性。

关键词: 通信技术; 认知无线电; 协作频谱感知; 频谱感知模型; D-S证据理论

中图分类号:TN929 文献标志码:A 文章编号:1671-5497(2016)04-1304-09

Region oriented spectrum sensing model for cognitive radio system

LUAN Lei^1,², ZHAO Xiao-hui², XU Yong-jun²

1.Department of Wireless Communication, Air Force Dalian Communication Sergeant School, Dalian 116600, China

2.College of Communication Engineering, Jilin University, Changchun 130012, China

Abstract

A Region-oriented Spectrum Sensing Model (RSSM) was proposed. First, the size of the sensing area of RSSM was deduced using path loss and fading margin theory. Then, in single-user spectrum sensing framework, the method of threshold setting and the impact of secondary user's location on the performance of spectrum sensing were analyzed. Furthermore, in hard decision-making cooperative spectrum sensing, the effect of the secondary user's dispersion on the performance of spectrum sensing was studied. Simulation results not only demonstrate the effectiveness and rationality of the proposed model, but also confirm the correctness of location information on the analysis of spectrum sensing performance.

Keyword: communication; cognitive radio; cooperative spectrum sensing; spectrum sensing model; D-S evidence theory

Show Figures

0 引言

频谱感知是认知无线电技术的基础^{[1, 2, 3]}, 具有快速准确的频谱感知能力是对高性能认知无线电设备的基本要求。目前, 频谱感知方法从是否协作角度上看可分为两类:单用户本地频谱感知和协作频谱感知。电磁环境中的多径效应、阴影衰落和噪声不确定性严重影响了系统的频谱感知性能^[4], 因此单用户频谱感知有时很难满足认知无线电系统要求。由于协作频谱感知能够大大提高频谱感知性能, 因此受到普遍关注^[5]。

目前, 多数学者在研究基于能量检测的频谱感知时, 都假定已知接收信号信噪比(SNR), 所得到的频谱感知性能是针对一个固定SNR来说的, 这就是面向信噪比的频谱感知模型。次用户接收信号的信噪比主要由主用户发射功率、次用户与主用户之间的距离以及信道状态决定, 如果已知主用户发射功率并且只考虑信道中的路径损耗, 将信噪比固定相当于假设所要感知的主用户全都位于以次用户为圆心的某圆内。然而在实际应用中, 主用户与次用户之间的距离是随机变化的, 将主用户的位置严格限定在一个圆内是不尽合理的, 在这一假设下设计出的频谱感知方法有时难以满足实际认知无线电系统要求。因此, 以主用户的位置可随机变化作为研究的前提更具有实际意义。另外, 由于协作频谱感知通过空间分集来提高频谱感知性能, 所以参与协作的次用户和主用户的位置必将对协作频谱感知性能产生影响, 因此, 位置信息的应用得到很多学者的关注。文献[6]在假设主用户位置信息的前提下, 推导出最佳的能量检测阈值, 然而通常情况下很难获得主用户的位置信息, 所以难以推广到实际应用中。文献[7]将随机几何网络模型引入到频谱感知研究中, 充分考虑了主用户网络和次用户网络拓扑结构的随机性, 将感知信息线性融合, 并采用Fisher线性判别法推导出线性系数。文献[8]根据次用户的相对位置信息来研究参与协作次用户的本地检测结果的相关性, 并建立一个低复杂度的次优融合准则。

已知的关于用户位置信息对频谱感知性能影响的研究基本上都是基于面向信噪比的频谱感知模型的, 本文尝试建立一种面向区域的频谱感知模型(Region oriented spectrum sensing model, RSSM), 并通过该模型从一个新的角度分析次用户的位置对频谱感知性能的影响, RSSM中检测目标不再是检测距次用户某一距离处是否存在主用户而是检测在某一区域中是否存在主用户, 此时主用户与次用户之间的距离是随机变化的, 所建模型实际上就是在以往研究的基础上, 补充了主用户与次用户的相对位置因素对频谱感知性能的影响, 使频谱感知模型更完备, 更符合实际应用场景。

1 系统模型

RSSM包含三个要素:一是需要被感知的主用户; 二是发起通信的次用户; 三是次用户的感知区域。RSSM就是指发起通信的次用户对感知区域进行检测, 判定其中是否存在主用户。合理划分感知区域既保证了次用户与主用户的正常通信, 又达到了充分提高频谱利用率的目的。感知区域太大将导致次用户感知灵敏度过高, 频谱利用率过低; 感知区域太小, 主用户与次用户之间容易相互干扰。次用户通常位于感知区域的中心, 限定感知区域相当于限定主用户与次用户之间距离的变化范围。由于距离对路径损耗的影响最为直接, 因此在RSSM中只考虑路径损耗对感知区域划分的影响。感知区域实质上是由次用户和主用户的发射功率等通信参数决定的。如图1所示, 其中有一个主用户 $\begin{matrix} PU 和 SU 一个次用户, R_{pi} \end{matrix}$ 为主用户干扰半径; $\begin{matrix} R_{pc} \end{matrix}$ 为主用户通信半径; $\begin{matrix} R_{si} \end{matrix}$ 为次用户干扰半径; $\begin{matrix} R_{sc} \end{matrix}$ 为次用户通信半径; $\begin{matrix} A \end{matrix}$ 代表频谱感知区域, 其半径 $\begin{matrix} R \end{matrix}$ 为:

$\begin{matrix} R = \max \{R_{pc} + R_{si}, R_{sc} + R_{pi}\} (1) \end{matrix}$

式中: $\begin{matrix} R_{pc} + R_{si} \end{matrix}$ 是只考虑次用户干扰主用户通信, 主用户能够正常通信时, 主用户与次用户之间的最小距离; $\begin{matrix} R_{sc} + R_{pi} \end{matrix}$ 是只考虑主用户干扰次用户通信, 次用户正常通信时, 主用户与次用户之间的最小距离。

多数文献都未考虑主用户对次用户的干扰, 而在实际应用中, 不仅要防止次用户干扰主用户, 也要避免主用户干扰次用户。图1描述的是一种特殊情况, 此时 $\begin{matrix} R = R_{pc} + R_{si} = R_{sc} + R_{pi}, \end{matrix}$ 在实际应用中, 这种情况非常少, 但是如果将图中的主用户看做一个正在通信的次用户, 那就有其特殊意义了。因为实际应用中不允许两个次用户使用同一个频谱空洞(Spectrum hole, SH)。

	Figure Option View Download New Window
	图1 频谱感知区域示意图Fig.1 Spectrum sensing region framwork

主用户的通信半径 $\begin{matrix} R_{pc} \end{matrix}$ 由主用户的发射功率和主用户接收机的灵敏度决定, 这两个参数是主用户系统建立时确定的, 基于路径损耗原理以及这两个参数就能得到 $\begin{matrix} R_{pc} \end{matrix}$ 。路径损耗值主要由距离、波长、天线高度和环境决定, 因为本文主要考查距离对路径损耗的影响, 所以采用如下简化的路径损耗模型^[9]:

$\begin{matrix} \{\begin{matrix} L = P_{pt} - P_{pr} = 121.98 + 20 lgd - 20 lgλ' \\ d > R', R' = 10^{\frac{20 lgλ' - 121.98}{20}} \end{matrix} (2) \end{matrix}$

式中: $\begin{matrix} d \end{matrix}$ 为接收机与发射机间的距离, 单位为km; $\begin{matrix} L \end{matrix}$ 为路径损耗, 单位为dB; $\begin{matrix} λ' \end{matrix}$ 为波长, 单位为m。

用 $\begin{matrix} P_{prmin} \end{matrix}$ 表示主用户接收机正常工作时接收功率 $\begin{matrix} P_{pr} \end{matrix}$ 的最小值, 即主用户接收灵敏度。无线信道是时变衰落信道, 所以接收信号的SNR(已将所有功率值进行噪声归一化处理, 所以信噪比和功率数值相等)是一个随机变量, $\begin{matrix} P_{pr} \end{matrix}$ 有时非常小, 因此为了保证通信可靠性, 必须使 $\begin{matrix} P_{pr} \end{matrix}$ 的最小值比 $\begin{matrix} P_{prmin} \end{matrix}$ 高出一些, 高出这部分的SNR就是衰落裕度SNR_pi, 体现了主用户接收机抵抗干扰的能力。在保证正常通信的前提下, 主用户发射机和主用户接收机之间的最大路径损耗为:

$\begin{matrix} L_{\max} = P_{pt} - P_{prmin} - SN R_{pi} (3) \end{matrix}$

这时主用户发射机和接收机之间的距离是主用户系统的最大通信距离。式(3)中的 $\begin{matrix} P_{pt} 、 P_{prmin} \end{matrix}$ 和SNR_pi对一个主用户系统来说是已知的, 根据式(2)和式(3)可得:

$\begin{matrix} \begin{matrix} R_{pc} = \\ 10 \exp (\frac{P_{pt} - P_{prmin} - SN R_{pi} - 121.98 + 20 lgλ'}{20}) (4) \end{matrix} \end{matrix}$

同理, 可求出:

$\begin{matrix} \begin{matrix} R_{sc} = \\ 10 \exp (\frac{P_{st} - P_{srmin} - SN R_{si} - 121.98 + 20 lgλ'}{20}) (5) \end{matrix} \end{matrix}$

式中: $\begin{matrix} P_{srmin} \end{matrix}$ 是次用户接收机灵敏度; SNR_si是次用户系统的衰落裕度。由衰落裕度原理可求出 $\begin{matrix} R_{si} \end{matrix}$ 和 $\begin{matrix} R_{pi} \end{matrix}$ 分别为:

$\begin{matrix} \begin{matrix} R_{si} = 10 \exp (\frac{P_{st} - SN R_{pi} - 121.98 + 20 lgλ'}{20}) (6) \\ R_{pi} = 10 \exp (\frac{P_{pt} - SN R_{si} - 121.98 + 20 lgλ'}{20}) (7) \end{matrix} \end{matrix}$

由式(1)(4)(5)(6)和式(7)得出频谱感知半径 $\begin{matrix} R \end{matrix}$ , 确定感知区域是应用RSSM的前提。

2 基于RSSM的单用户能量检测

文献[10]指出, 在非衰落加性高斯白噪声信道中基于能量检测的单用户频谱感知性能为:

$\begin{matrix} \begin{matrix} P_{f} = \frac{Γ (u, \frac{λ}{2})}{Γ (u)} = H_{u} (λ) (8) \\ P_{d} = Q_{u} (\sqrt[]{2 γ}, \sqrt[]{λ}) (9) \end{matrix} \end{matrix}$

式中: $\begin{matrix} P_{f} 为虚拟警概率; P_{d} 为检测概率; γ \end{matrix}$ 是接受信号信噪比的瞬时值; $\begin{matrix} λ \end{matrix}$ 是检测阈值; $\begin{matrix} u \end{matrix}$ 是检测带宽和检测时间的乘积; $\begin{matrix} Γ (\cdot, \cdot) \end{matrix}$ 是不完全Gamma函数; $\begin{matrix} Γ (\cdot) \end{matrix}$ 是完全Gamma函数; $\begin{matrix} H_{u} (λ) 是 λ \end{matrix}$ 的函数。

由于虚警概率 $\begin{matrix} P_{f} \end{matrix}$ 与 $\begin{matrix} γ \end{matrix}$ 无关, 所以它与检测区域的大小也无关, 用 $\begin{matrix} P_{fA} \end{matrix}$ 表示次用户对 $\begin{matrix} A \end{matrix}$ 中主用户的虚警概率, 则有 $\begin{matrix} P_{fA} = P_{f} 。 \end{matrix}$ 因为检测概率 $\begin{matrix} P_{d} \end{matrix}$ 与 $\begin{matrix} γ \end{matrix}$ 有关, 所以检测区域的大小将对 $\begin{matrix} P_{d} \end{matrix}$ 产生影响。假设在 $\begin{matrix} A \end{matrix}$ 中有一个主用户, 主用户可在 $\begin{matrix} A \end{matrix}$ 中的任何位置出现, 那么主用户与次用户的距离 $\begin{matrix} d \end{matrix}$ 就是一个随机变量, 为了便于分析, 假设 $\begin{matrix} d \end{matrix}$ 服从均匀分布, 其概率密度函数为:

$\begin{matrix} f (d) = \{\begin{matrix} \frac{1}{R - R'}, R' < d \leq R \\ 0, 其他 \end{matrix} (10) \end{matrix}$

显然, 此时主用户出现在 $\begin{matrix} A \end{matrix}$ 上任何位置的概率是相等的。假设 $\begin{matrix} λ' \end{matrix}$ 和 $\begin{matrix} P_{pt} \end{matrix}$ 为已知, 由式(2)可得:

$\begin{matrix} γ (d) = P_{pt} - 121.98 - 20 lgd + 20 lgλ' (11) \end{matrix}$

由式(8)得阈值:

$\begin{matrix} λ = H_{u}^{- 1} (P_{f}) (12) \end{matrix}$

将式(11)(12)带入式(9)得:

$\begin{matrix} P_{d} = Q_{u} (\sqrt[]{2 γ (d)}, \sqrt[]{H_{u}^{- 1} (P_{f})}) (13) \end{matrix}$

假设 $\begin{matrix} P_{f} 、 P_{pt} \end{matrix}$ 和 $\begin{matrix} \end{matrix}$ λ'是已知量,而d是一个随机变量, 所以如果一个主用户以等概率出现在 $\begin{matrix} A \end{matrix}$ 中, 那么次用户能够检测到这个主用户的概率 $\begin{matrix} P_{dA} \end{matrix}$ 为:

$\begin{matrix} P_{dA} = \frac{1}{R - R'} \int_{R}^{'} Q_{u} (\sqrt[]{2 γ (x)}, \sqrt[]{H_{u}^{- 1} (P_{f})}) dx (14) \end{matrix}$

瑞利衰落信道中, 接收信号的信噪比是一个随机变量, 其概率密度函数为^[10]:

$\begin{matrix} f (γ) = \frac{1}{γ'} \exp (- \frac{γ}{γ'}) (15) \end{matrix}$

式中: $\begin{matrix} γ' \end{matrix}$ 是接收信号信噪比的均值, 取决于发射功率和路径损耗的大小, 表示为:

$\begin{matrix} γ' = P_{pt} - 121.98 - 20 lgd + 20 lgλ' (16) \end{matrix}$

同时考虑瑞利衰落和路径损耗两个因素的情况下, 检测概率 $\begin{matrix} P_{d} \end{matrix}$ 为:

$\begin{matrix} P_{d} = \int_{0}^{\infty} Q_{u} (\sqrt[]{2 γ}, \sqrt[]{λ}) f (γ) dγ (17) \end{matrix}$

将式(12)(15)带入式(17)得:

$\begin{matrix} \begin{matrix} P_{d} (d) = \int_{0}^{\infty} Q_{u} (\sqrt[]{2 x}, \sqrt[]{H_{u}^{- 1} (P_{f})}) \times \\ \frac{1}{γ' (d)} \exp (- \frac{x}{γ' (d)}) dx (18) \end{matrix} \end{matrix}$

该次用户对检测区域 $\begin{matrix} A \end{matrix}$ 的检测概率 $\begin{matrix} P_{dA} \end{matrix}$ 为:

$\begin{matrix} \begin{matrix} P_{dA} = \frac{1}{R - R'} \int_{R}^{'} \int_{0}^{\infty} Q_{u} (\sqrt[]{2 x}, \sqrt[]{H_{u}^{- 1} (p_{f})}) \times \\ \frac{1}{γ' (y)} \exp (- \frac{x}{γ' (y)}) dxdy (19) \end{matrix} \end{matrix}$

定义 $\begin{matrix} g (y) \end{matrix}$ 为:

$\begin{matrix} \begin{matrix} g (y) = \int_{0}^{\infty} Q_{u} (\sqrt[]{2 x}, \sqrt[]{H_{u}^{- 1} (p_{f})}) \times \\ \frac{1}{γ' (y)} \exp (- \frac{x}{γ' (y)}) dx (20) \end{matrix} \end{matrix}$

根据式(20)可将式(19)化简为:

$\begin{matrix} P_{dA} = \frac{1}{R - R'} \int_{R}^{'} g (y) dy (21) \end{matrix}$

显然 $\begin{matrix} g (y) \end{matrix}$ 在 $\begin{matrix} [R', R] \end{matrix}$ 上是连续的, 由积分中值定理可知, 必存在一点 $\begin{matrix} ξ \in [R', R], 使 P_{dA} = g (ξ) 。 \end{matrix}$ 因为主用户距离次用户越近 $\begin{matrix} P_{d} \end{matrix}$ 越大, 令 $\begin{matrix} P_{dR'} = P_{d} (R'), P_{dR} = P_{d} (R), \end{matrix}$ 所以在相同阈值 $\begin{matrix} λ \end{matrix}$ 下有 $\begin{matrix} P_{dR} < P_{dA} < P_{dR'} 。 \end{matrix}$ 设定阈值时, 若使 $\begin{matrix} 0.99 < P_{dR} < P_{dA} < P_{dR'}, \end{matrix}$ 此时次用户对感知区域上主用户的检测概率很高, 但是如果主用户出现在距次用户较近的位置, $\begin{matrix} P_{d} \end{matrix}$ 将非常大, 甚至接近于1, 这说明 $\begin{matrix} λ \end{matrix}$ 设定得过小, 这将使 $\begin{matrix} P_{f} \end{matrix}$ 非常大, 此时频谱利用率过低。如果为了降低 $\begin{matrix} P_{f} \end{matrix}$ 而使 $\begin{matrix} λ \end{matrix}$ 变得太大, 又将使距离次用户较远处的主用户的检测概率变得过于小, 无法满足需要, 这说明当主用户位置随机变化时, 由于面向信噪比频谱感知模型无法从全局的角度衡量频谱感知性能, 所以难以选择合适的 $\begin{matrix} λ \end{matrix}$ , 这是传统的面向信噪比频谱感知的弊病。通过上面的分析, 可以得出, 在设定 $\begin{matrix} λ \end{matrix}$ 时, 合理的选择是使 $\begin{matrix} P_{dA} = 0.99, \end{matrix}$ 这样既保证了在感知区域 $\begin{matrix} A \end{matrix}$ 上主用户以足够高的概率被感知到, 又保证了SH的利用率。

下面探讨次用户位置对 $\begin{matrix} P_{dA} \end{matrix}$ 的影响。设次用户为 $\begin{matrix} A \end{matrix}$ 中任意一点 $\begin{matrix} (ρ, θ), \end{matrix}$ 原点为极点, 由于 $\begin{matrix} A \end{matrix}$ 是一个对称区域, $\begin{matrix} θ \end{matrix}$ 对 $\begin{matrix} P_{dA} \end{matrix}$ 无影响, 所以将次用户坐标简化为 $\begin{matrix} (ρ, 0) \end{matrix}$ 。主用户极坐标设为 $\begin{matrix} (ρ_{p}, θ_{p}), ρ_{p} \end{matrix}$ 和 $\begin{matrix} θ_{p} \end{matrix}$ 的概率密度函数分别表示为:

$\begin{matrix} \begin{matrix} f (ρ_{p}) & = \{\begin{matrix} \frac{1}{R - R'}, 0 < R' < ρ_{p} < R \\ 0, 其他 \end{matrix} (22) \\ g (θ_{p}) & = \frac{1}{2 π}, 0 < θ_{p} < 2 π (23) \end{matrix} \end{matrix}$

可证明 $\begin{matrix} E [γ'] \end{matrix}$ 是 $\begin{matrix} ρ \end{matrix}$ 的递减函数(见附录), 也就是说次用户离中心越远, 次用户接收信噪比的均值越小, 其漏检率就越高, 所以在同一阈值下, 次用户位于原点时, 对 $\begin{matrix} A \end{matrix}$ 上主用户的检测概率最大。

3 基于RSSM的协作频谱感知

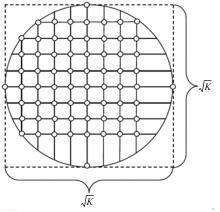
为了便于分析, 将感知区域离散化, 如图2所示。在感知区域上画网格, 平行横线之间的距离和平行竖线之间的距离相等, 横线和竖线的交点记为 $\begin{matrix} i, i = 1, 2, \dots, K 。 \end{matrix}$ 假设感知区域中只有一个主用户, 并且只能在这 $\begin{matrix} K \end{matrix}$ 个交点上出现, 在每个交点出现的概率相等, 当 $\begin{matrix} K \end{matrix}$ 趋于无穷大时, 感知区域就转变为连续区域。假设感知区域中有两组次用户, 第一组由位于同一点的 $\begin{matrix} n \end{matrix}$ 个次用户组成, 第二组中有 $\begin{matrix} n \end{matrix}$ 个次用户, 其中一个次用户与第一组中次用户的位置相同, 其余 $\begin{matrix} n - 1 \end{matrix}$ 个次用户分散在感知区域的不同位置。下面用D-S理论分析基于RSSM的“ OR” 准则和“ AND” 准则协作频谱感知中次用户的分散性对协作频谱感知性能的影响。

	Figure Option View Download New Window
	图2 感知区域离散化示意图Fig.2 Discretized sensing area

3.1 基于RSSM的“ OR” 准则频谱感知

设 $\begin{matrix} Ω_{u} = {c_{u 1}, \dots, c_{uk}, m_{u 1}, \dots, m_{uk}} \end{matrix}$ 是第 $\begin{matrix} u \end{matrix}$ 个次用户对应的识别框架, $\begin{matrix} {c_{ui}} \end{matrix}$ 是主用户在 $\begin{matrix} i \end{matrix}$ 点时第 $\begin{matrix} u \end{matrix}$ 个次用户感知到该主用户, $\begin{matrix} {m_{ui}} \end{matrix}$ 是主用户在 $\begin{matrix} i \end{matrix}$ 点时第 $\begin{matrix} u \end{matrix}$ 个次用户未感知到该主用户, 这样的识别框架共有 $\begin{matrix} n \end{matrix}$ 个。每个识别框架中都有 $\begin{matrix} 2 K \end{matrix}$ 个焦元, 分别为 $\begin{matrix} {c_{ui}} \end{matrix}$ 和 $\begin{matrix} {m_{ui}}, i = 1, 2, \dots, K; u = 1, 2, \dots, n 。 \end{matrix}$ 因为每组次用户都是由 $\begin{matrix} n \end{matrix}$ 个次用户组成的, 所以每组次用户对应 $\begin{matrix} n \end{matrix}$ 个证据, 每个次用户对应一个基本概率分配(Basic probability assignment, BPA)函数, 设 $\begin{matrix} M_{gu} (x) \end{matrix}$ 是第 $\begin{matrix} g \end{matrix}$ 组的第 $\begin{matrix} u \end{matrix}$ 个次用户对应的基本概率分配函数。设 $\begin{matrix} Ω_{g} = {{\bar{c}}_{g 1}, \dots, {\bar{c}}_{gk}, {\bar{m}}_{g 1}, \dots, {\bar{m}}_{gk}} \end{matrix}$ 是第 $\begin{matrix} g \end{matrix}$ 组次用户对应的识别框架, $\begin{matrix} \{{\bar{c}}_{gi}\} \end{matrix}$ 是主用户在 $\begin{matrix} i \end{matrix}$ 点时第 $\begin{matrix} g \end{matrix}$ 组次用户感知到该主用户, $\begin{matrix} \{{\bar{m}}_{gi}\} \end{matrix}$ 是主用户在 $\begin{matrix} i \end{matrix}$ 点时第 $\begin{matrix} g \end{matrix}$ 组次用户未感知到该主用户, 设 $\begin{matrix} M_{g} (x) \end{matrix}$ 是第 $\begin{matrix} g \end{matrix}$ 组次用户的基本概率分配函数。

假设每个次用户的阈值相同, 并使总的虚警概率为0.1。设单个次用户的基本概率分配函数为:

$\begin{matrix} \{\begin{matrix} M_{gu} ({c_{ui}}) = \frac{p_{d} (d_{ui})}{K} \\ M_{gu} ({m_{ui}}) = \frac{1 - p_{d} (d_{ui})}{K} \end{matrix} (24) \end{matrix}$

式中: $\begin{matrix} d_{ui} \end{matrix}$ 是第 $\begin{matrix} u \end{matrix}$ 个次用户与点 $\begin{matrix} i \end{matrix}$ 之间的距离。

对于“ OR” 准则协作频谱感知, D-S理论的推理规则可表示为:

$\begin{matrix} if E_{gi} t h enC = {{\bar{c}}_{gi}} CF = {h_{i}} (25) \end{matrix}$

式中:证据 $\begin{matrix} E_{gi} \end{matrix}$ 是 $\begin{matrix} n \end{matrix}$ 个独立证据的析取, 其含义是当主用户在 $\begin{matrix} i \end{matrix}$ 点时, 第 $\begin{matrix} g \end{matrix}$ 组中有次用户检测到该主用户, $\begin{matrix} E_{gi} \end{matrix}$ 可表示为:

$\begin{matrix} E_{gi} = E_{1 i} \lor E_{2 i} \lor \dots \lor E_{ni} (26) \end{matrix}$

式中: $\begin{matrix} E_{ui} = \{c_{ui}\}, u = 1, 2, \dots, n; \end{matrix}$ CF是可信度因子, 因为式(25)是一个确定性推理, 所以 $\begin{matrix} h_{i} = 1, C \end{matrix}$ 是结论, 其基本概率分配函数为:

$\begin{matrix} M_{g} (\{{\bar{c}}_{gi}\}) = CER (E_{gi}) \times h_{i} (27) \end{matrix}$

式中: $\begin{matrix} CER (E_{gi}) \end{matrix}$ 是 $\begin{matrix} E_{gi} \end{matrix}$ 的信任度函数, 表示证据 $\begin{matrix} E_{gi} \end{matrix}$ 的确定性, 根据证据析取原理可得:

$\begin{matrix} \begin{matrix} CER (E_{gi}) = \max {CER (\{c_{1 i}\}), \\ C ER (\{c_{2 i}\}), \dots, CER (\{c_{ni}\})} (28) \end{matrix} \end{matrix}$

式中: $\begin{matrix} CER (\{c_{ui}\}) \end{matrix}$ 是 $\begin{matrix} \{c_{ui}\} \end{matrix}$ 的信任度函数, 描述了 $\begin{matrix} \{c_{ui}\} \end{matrix}$ 的确定性, $\begin{matrix} CER (\{c_{ui}\}) \end{matrix}$ 为:

$\begin{matrix} \begin{matrix} CER (\{c_{ui}\}) = Bel (\{c_{ui}\}) + \frac{|\{c_{ui}\}|}{|Ω_{u}|} \times \\ [Pl (\{c_{ui}\}) - Bel (\{c_{ui}\})] (29) \end{matrix} \end{matrix}$

式中: $\begin{matrix} Bel (\{c_{ui}\}) \end{matrix}$ 是 $\begin{matrix} \{c_{ui}\} \end{matrix}$ 的信任函数; $\begin{matrix} Pl (\{c_{ui}\}) \end{matrix}$ 是 $\begin{matrix} \{c_{ui}\} \end{matrix}$ 的似然函数; $\begin{matrix} |\{c_{ui}\}| \end{matrix}$ 和 $\begin{matrix} |Ω_{u}| \end{matrix}$ 分别是 $\begin{matrix} \{c_{ui}\} \end{matrix}$ 和 $\begin{matrix} Ω_{u} \end{matrix}$ 中元素的个数, 根据D-S理论得:

$\begin{matrix} \begin{matrix} Bel (\{c_{ui}\}) = \sum_{B \subseteq \{c_{ui}\}} M_{gu} (B), 对所有 B \in Ω_{u} (30) \\ Pl (\{c_{ui}\}) = \sum_{B ⋂ \{c_{ui}\} \neq φ} M_{gu} (B), 对所有 B \in Ω_{u} (31) \end{matrix} \end{matrix}$

因为 $\begin{matrix} Ω_{u} \end{matrix}$ 中的 $\begin{matrix} c_{ui} \end{matrix}$ 与 $\begin{matrix} m_{ui} \end{matrix}$ 都是互斥的, 所以:

$\begin{matrix} Pl (E_{ui}) = Bel (E_{ui}) = M_{gu} (\{c_{ui}\}) (32) \end{matrix}$

由式(29)和式(32)可得 $\begin{matrix} CER (\{c_{ui}\}) = M_{gu} (\{c_{ui}\}), \end{matrix}$ 那么式(28)就被转换为:

$\begin{matrix} \begin{matrix} CER (E_{gi}) = \\ \max \{M_{gu} (\{c_{1 i}\}), M_{gu} (\{c_{2 i}\}), \dots, M_{g u} (\{c_{ni}\})\} (33) \end{matrix} \end{matrix}$

因为 $\begin{matrix} P_{d} (d_{ui}) \end{matrix}$ 是 $\begin{matrix} d_{ui} \end{matrix}$ 的单调递减函数, 设第 $\begin{matrix} g \end{matrix}$ 组中次用户与点 $\begin{matrix} i \end{matrix}$ 之间距离的最小值为 $\begin{matrix} d_{gi} = \min \{d_{ui}\}, u = 1, 2, \dots, n, \end{matrix}$ 那么:

$\begin{matrix} CER (E_{gi}) = p_{d} (d_{gi}) / K (34) \end{matrix}$

其含义是 $\begin{matrix} i \end{matrix}$ 点上有主用户时, 证据 $\begin{matrix} E_{gi} \end{matrix}$ 的确定性等于离 $\begin{matrix} i \end{matrix}$ 点最近的次用户感知到 $\begin{matrix} i \end{matrix}$ 点上主用户的可信度。对于第一组次用户, 由于 $\begin{matrix} n \end{matrix}$ 个次用户位于同一点, 所以 $\begin{matrix} d_{1 i} = d_{ui} 。 \end{matrix}$ 而第二组中的 $\begin{matrix} n \end{matrix}$ 个次用户分散在感知区域的不同位置, 由于其中一个次用户和第一组中次用户位于相同位置, 则可得:

$\begin{matrix} d_{1 i} \geq d_{2 i} (35) \end{matrix}$

由式(34)(35)和 $\begin{matrix} P_{d} (d_{ui}) \end{matrix}$ 的单调性可得:

$\begin{matrix} CER (E_{1 i}) \leq CER (E_{2 i}) (36) \end{matrix}$

由式(27)(36)可得:

$\begin{matrix} M_{1} (\{{\bar{c}}_{1 i}\}) \leq M_{2} (\{{\bar{c}}_{2 i}\}) (37) \end{matrix}$

集合 $\begin{matrix} \{{\bar{c}}_{g 1}, \dots, {\bar{c}}_{gK}\} \end{matrix}$ 的信任函数为:

$\begin{matrix} Bel (\{{\bar{c}}_{g 1}, \dots, {\bar{c}}_{gK}\}) = \overset{K}{\sum_{i = 1}} M_{g} (\{{\bar{c}}_{gi}\}) (38) \end{matrix}$

式(38)描述了感知区域上只有一个主用户时, 第 $\begin{matrix} g \end{matrix}$ 组次用户感知到该主用户的信任程度, 其值越大说明该组次用户的感知性能越好。由式(37)和式(38)可得:

$\begin{matrix} Bel (\{{\bar{c}}_{11}, \dots, {\bar{c}}_{1 K}\}) < Bel (\{{\bar{c}}_{21}, \dots, {\bar{c}}_{2 K}\}) (39) \end{matrix}$

由式(39)可知, 第二组次用户的感知性能比第一组次用户的感知性能好, 所以基于RSSM的“ OR” 准则协作频谱感知, 次用户越分散, 感知性能越好。

3.2 基于RSSM的“ AND” 准则频谱感知

对于“ AND” 准则协作频谱感知, D-S理论的推理规则表示为:

$\begin{matrix} ifE'_{gi} t h enC = \{\bar{c}'_{gi}\} CF = \{h_{i}\} (40) \end{matrix}$

式中:证据 $\begin{matrix} E'_{gi} \end{matrix}$ 是 $\begin{matrix} n \end{matrix}$ 个独立证据的合取, 其含义是当主用户在 $\begin{matrix} i \end{matrix}$ 点时, 第 $\begin{matrix} g \end{matrix}$ 组中所有次用户都检测到该主用户, $\begin{matrix} E'_{gi} \end{matrix}$ 可表示为:

$\begin{matrix} E'_{gi} = E_{1 i} \land E_{2 i} \land \dots \land E_{ni} (41) \end{matrix}$

式中: $\begin{matrix} E_{ui} = \{c_{ui}\}, u = 1, 2, \dots, n; \end{matrix}$ 因为式(41)是一个确定性推理, 所以 $\begin{matrix} h_{i} = 1, C \end{matrix}$ 是结论, 其基本概率分配函数为:

$\begin{matrix} M_{g} ({\bar{c}'_{gi}}) = CER (E'_{gi}) \times h_{i} (42) \end{matrix}$

式中: CER(E'_gi)是E'_gi 的信任度函数,表示证据E'_gi的确定性, 根据证据合取原理可得:

$\begin{matrix} CER (E'_{gi}) = \min \{\begin{matrix} CER ({c_{1 i}}), \\ CER ({c_{2 i}}), \dots, CER ({c_{ni}}) \end{matrix}\} (43) \end{matrix}$

由证据理论可知 $\begin{matrix} CER (E_{ui}) = M_{gu} ({c_{ui}}), \end{matrix}$ 那么式(43)可转化为:

$\begin{matrix} \begin{matrix} CER (E_{gi}) = \min {M_{gu} ({c_{1 i}}), \\ M_{gu} ({c_{2 i}}), \dots, M_{gu} ({c_{ni}})} (44) \end{matrix} \end{matrix}$

设d'_gi=max{d_ui } 是第g组中次用户与点i之间距离的最大值,式中u=1,2,…,n,由于P_d (d_ui)是d_ui的单调递减函数,那么CER(E'_gi)表示为:

$\begin{matrix} CER (E'_{gi}) = \frac{P_{d} (d'_{gi})}{K} (45) \end{matrix}$

其含义是 i点上有主用户时,证据E'_gi的确定性等于离i点最远的次用户感知到该主用户的可信度。对第一组次用户来说,由于n个次用户位于同一点,所以d'_1i=d_ui 。第二组中n个次用户分散在感知区域的不同位置, 并且其中有一个次用户与第一组中次用户的位置相同, 则可得:

$\begin{matrix} d'_{1 i} \leq d'_{2 i} (46) \end{matrix}$

由式(44)(46)和 $\begin{matrix} P_{d} (d_{ui}) \end{matrix}$ 的单调性可得:

$\begin{matrix} CER (E'_{1 i}) \geq CER (E'_{2 i}) (47) \end{matrix}$

由式(42)(47)可得:

$\begin{matrix} M_{1} ({\bar{c}'_{1 i}}) \geq M_{2} ({\bar{c}'_{2 i}}) (48) \end{matrix}$

由式(38)(48)可得:

$\begin{matrix} Bel ({\bar{c}'_{11}, \dots, \bar{c}'_{1 K}}) > Bel ({\bar{c}'_{21}, \dots, \bar{c}'_{2 K}}) (49) \end{matrix}$

由式(49)可知, 第一组次用户的感知性能比第二组次用户的感知性能好, 所以基于RSSM的“ AND” 准则协作频谱感知, 次用户越集中, 感知性能越好。因为 $\begin{matrix} d'_{1 i} = d_{1 i}, \end{matrix}$ 并且由式(34)(45)可得:

$\begin{matrix} CER (E'_{1 i}) = CER (E_{1 i}) (50) \end{matrix}$

由式(36)(47)(50)可得:

$\begin{matrix} \begin{matrix} CER (E_{2 i}) \geq CER (E_{1 i}) = \\ CER (E'_{1 i}) \geq CER (E'_{2 i}) (51) \end{matrix} \end{matrix}$

由式(27)(42)(51)可得;

$\begin{matrix} \begin{matrix} M_{2} ({{\bar{c}}_{2 i}}) \geq M_{1} ({{\bar{c}}_{1 i}}) = \\ M_{1} ({\bar{c}'_{1 i}}) \geq M_{2} ({\bar{c}'_{2 i}}) (52) \end{matrix} \end{matrix}$

由式(38)(52)可得:

$\begin{matrix} \begin{matrix} Bel ({{\bar{c}}_{21}, \dots, {\bar{c}}_{2 K}}) > Bel ({{\bar{c}}_{11}, \dots, {\bar{c}}_{1 K}}) = \\ Bel ({\bar{c}'_{1 i}, \dots, \bar{c}'_{1 K}}) > Bel ({\bar{c}'_{2 i}, \dots, \bar{c}'_{2 K}}) (53) \end{matrix} \end{matrix}$

由式(53)可知, 无论次用户集中还是分散, 基于RSSM的协作频谱感知, 采用“ OR” 准则都比采用“ AND” 准则感知性能好。

4 仿真验证

4.1 仿真条件

首先确定感知区域A。设主用户通信系统中P_pt是120 dB· m, $\begin{matrix} P_{prmin} \end{matrix}$ 是9.5425 dB· m, SNR_pi是18.93 dB; 次用户通信系统中 $\begin{matrix} P_{st} \end{matrix}$ 是120 dB· m, $\begin{matrix} P_{srmin} \end{matrix}$ 是9.5425 dB· m, SNR_si是18.9351 dB。信号波长 $\begin{matrix} λ' \end{matrix}$ 为1/6 m。由式(4)(5)(6)和式(7)可得R_pc和R_sc等于1 km, R_pi和R_si等于1.5 km, 再由式(1)求得感知半径等于2.5 km。下面基于这些参数进行仿真。另外, 设时间带宽积为5, 并且所有检测概率和虚警概率的理论值都是根据式(8)(9)和式(17)计算得来的, 仿真值是通过10⁶次蒙特卡洛仿真计算的。

4.2 单用户频谱感知

图3描述了单用户频谱感知中, 虚警概率为0.1时, 次用户位置对漏检概率的影响。设次用户的极坐标为 (ρ,θ),由于感知区域是中心对称的,所以令θ=0,只需考虑ρ对感知性能的影响。由图3可知,漏检概率P_m随ρ的增大而增大, 这与第2节的分析相符, 可理解为次用户离感知区域中心越远, 主用户在次用户附近区域出现的概率越小, 次用户检测主用户的难度越大, 发生漏检的概率越大。

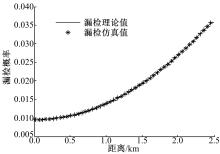	Figure Option View Download New Window
	图3 基于RSSM次用户位置对单用户频谱感知性能的影响Fig.3 Performance of single user spectrum sensing versus secondary user's location under RSSM

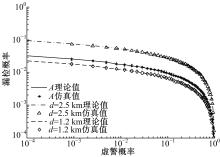	Figure Option View Download New Window
	图4 基于RSSM和SNR模型单用户频谱感知的补充ROCFig.4 Performance of ROC based on RSSM and SNR model in single user scenario

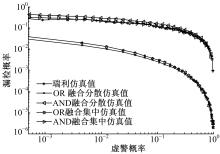
图4是基于RSSM和面向信噪比频谱感知模型在加性高斯白噪声加瑞利衰落信道中的补充ROC。传统的面向信噪比的频谱感知模型中, 主用户与次用户之间的距离固定不变, 例如假设主用户与次用户之间距离为1.2 km, 设定阈值为 $\begin{matrix} λ_{1, 2} 时漏检概率为 0.01, 虚警概率为 P_{f 1, 2} = 0.002 \end{matrix}$ (远小于0.1); 假设主用户与次用户之间距离为2.5 km, 设定阈值为 $\begin{matrix} λ_{2.5} 时漏检概率为 0.01 时, 虚警概率为 P_{f 2.5} = 0.342 \end{matrix}$ (大于0.1)。显然 , 设定主用户和次用户之间的距离不同将导致设定的阈值不同, 所得到的虚警概率就不同, 从图4可知, 所得到的虚警概率有时满足要求, 有时不满足要求, 因此面向信噪比频谱感知模型中难以找到一个合适的阈值。从图4可知, 基于RSSM的频谱感知, 漏检概率为0.01时虚警概率 $\begin{matrix} P_{fA} = 0.083 \end{matrix}$ (小于并且接近0.1)恰好满足要求, 由此可见基于RSSM设定的阈值是合理的。

4.3 硬决策协作频谱感知

图5中给出了基于RSSM的三组次用户的频谱感知特性, 第一组中只有一个位于感知区域中心的次用户; 第二组中有5个次用户, 它们的极坐标分别为(0, 0)、(1, 0)、(1, π /2)、(1, π )和(1, 3π /2), 代表一组分散的次用户; 第三组中有5个次用户, 它们的极坐标分别为(0, 0)、(1, 0)、(1, 0)、(1, 0)和(1, 0), 代表一组集中的次用户。第一组次用户补充ROC的理论值曲线和仿真值曲线完全重合, 并且与另外两组次用户相比, 对于同一虚警概率, 该组对应的漏检概率最大, 说明“ OR” 准则协作频谱感知性能优于单用户频谱感知性能。图5中的理论值曲线是根据传统的“ OR” 准则理论^[11]得到的, 第二组的理论值曲线和第三组的理论值曲线重合, 说明传统的“ OR” 准则理论无法反映次用户的分散性对频谱感知性能的影响。第三组的仿真值曲线在第二组仿真值曲线上方, 说明次用户分散时的漏检概率比集中时的漏检概率小, 这与第3节分析的结论相符, 第二组和第三组中仿真值曲线都在理论值曲线上方, 说明传统的“ OR” 准则融合理论不适用于RSSM。

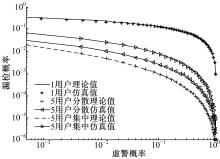	Figure Option View Download New Window
	图5 基于RSSM的“ OR” 准则协作频谱感知性能Fig.5 Performance of cooperative spectrum sensing based on RSSM under ‘ OR’ criteria

为了说明对称性和分散性对频谱感知性能的影响, 假设感知区域中有5个次用户, 它们的极坐标分别为(0,0)、(1,θ)、(1,θ/4、(1,θ/2)和(1,3θ/4),θ∈(0,2π]。由图6可知,Q_m是θ的单调递减函数。θ=2π时次用户的分散性和对称性最好, 感知性能也最好。

	Figure Option View Download New Window
	图6 基于RSSM的“ OR” 准则协作频谱感知恒虚警时极角θ 对Q_m的影响Fig.6 Performance of polar angle under cooperative spectrum sensing based on RSSM under ‘ OR’ criteria

	Figure Option View Download New Window
	图7 基于RSSM“ AND” 准则协作频谱感知性能Fig.7 Performance of cooperative spectrum sensing based on RSSM under ‘ AND’ criteria

图7是三组次用户的"AND"准则协作频谱感知性能曲线。假设感知区域中有三组次用户, 第一组中只有一个位于(0, 0)的次用户, 该组代表单个次用户; 第二组中有5个次用户, 它们的极坐标为(0, 0)、(1, 0)、(1, π /2)、(1, π )和(1, 3π /2), 该组代表位置分散的次用户; 第三组中有5个次用户, 它们的极坐标为(0, 0)、(1, 0)、(1, 0)、(1, 0)和(1, 0), 该组代表位置集中的次用户。由图7可知, 单用户感知时, 理论值曲线与仿真值曲线重合, 并且在另外两组次用户仿真值曲线下方, 说明单用户频谱感知的性能优于“ AND” 准则协作频谱感知的性能。第二组和第三组次用户的理论值曲线重合, 并且位于这两组次用户仿真值曲线的上方, 说明传统“ AND” 融合理论无法反映次用户分散性对频谱感知性能的影响, 并且不适用于RSSM。第二组次用户的仿真值曲线在第三组次用户仿真值曲线的上方, 说明此时, 次用户越集中感知性能越好。

	Figure Option View Download New Window
	图8 次用户极径固定极角对漏检概率的影响Fig.8 Performance of undetected probability versus polar radius fixed polar angel of SUs

图8进一步证实了基于RSSM的“ AND” 准则协作频谱感知中次用户的分散性对频谱感知性能的影响。感知区域中有5个次用户, 它们的极坐标分别为(0,0)、(1,θ)、(1,θ/4)、(1,θ/2)和(1,3θ/4),θ∈(0,2π]。由图8可知,Q_m是θ的单调递增函数。θ=2π时次用户分散性最大, 漏检概率最大。理论值为常量并且始终比仿真值小, 说明传统“ AND” 融合理论无法反映次用户分散性对频谱感知性能的影响。

因为传统的“ OR” 准则和“ AND” 准则协作频谱感知理论不适用于RSSM, 所以图9中只给出这两种融合准则的仿真结果。设感知区域中有三组次用户, 第一组只有一个次用户, 坐标为(0, 0), 代表单用户感知; 第二组中有5个次用户, 它们的极坐标分别为(0, 0)、(1, 0)、(1, π /2)、(1, π )和(1, 3π /2), 代表分散的次用户; 第三组中有5个次用户, 它们极坐标分别为(0, 0)、(0.1, 0)、(0.1, 0)、(0.1, 0)和(0.1, 0), 代表集中的次用户。由图9可知, 无论次用户集中还是分散, “ OR” 准则的漏检概率都比“ AND” 准则的漏检概率小, 而且次用户分散分布并采用“ OR” 准则融合时漏检概率最小, 即感知性能最好。

	Figure Option View Download New Window
	图9 “ AND” 准则和“ OR” 准则补充ROCFig.9 Performance of ROC under ‘ AND’ and ‘ OR’ criterion

5 结束语

本文建立的RSSM与传统面向信噪比的频谱感知模型相比, 实用性更强。在阈值设定方面, 基于RSSM的阈值设定方法更加合理, 有效提高了认知无线电系统的感知性能。另外, 分析发现基于RSSM的频谱感知中, 主用户和次用户的位置信息按一定规律影响感知性能:在单用户频谱感知中, 次用户在感知区域中心时频谱感知性能最好; 在“ OR” 准则协作频谱感知中, 次用户越分散感知性能越好, 而“ AND” 准则协作频谱感知中, 次用户越集中感知性能越好, 并且无论次用户如何分布, “ OR” 准则频谱感知的感知性能都优于“ AND” 准则频谱感知的感知性能, 这些结论无疑对次用户的选择有一定的指导意义。

附录

对E[γ']是ρ的递减函数的证明

设次用户极坐标为(ρ,0),主用户的极坐标为(ρ_p,θρ_p),由余弦定理得:

$\begin{matrix} \begin{matrix} k (ρ_{p}, θ_{p}, ρ) = ρ_{p}^{2} - 2 ρ_{p} ρcos θ_{p} + ρ^{2} (54) \\ d = \sqrt[]{k (ρ_{p}, θ_{p}, ρ)} (55) \end{matrix} \end{matrix}$

将式(54)(55)带入式(16)得:

$\begin{matrix} \begin{matrix} γ' & = - 10 \lg [k (ρ_{p}, θ_{p}, ρ)] + C (56) \\ C & = P_{pt} - 121.98 + 20 lgλ' (57) \end{matrix} \end{matrix}$

当 $\begin{matrix} ρ_{p} = R, θ_{p} = π, ρ = R 时 k (ρ_{p}, θ_{p}, ρ) 的值最大为 4 R^{2}; 当 ρ_{p} = R', θ_{p} = 0, ρ = 0 时 k (ρ_{p}, θ_{p}, ρ) 的值最小为 R_{0}^{2} 。点 (4 R^{2}, \lg 4 R^{2}) 和点 (R_{0}^{2}, \lg R_{0}^{2}) 确定一条直线 l, \end{matrix}$ 其方程式为:

$\begin{matrix} l (k) = \frac{\lg 4 R^{2} - \lg R_{0}^{2}}{4 R^{2} - R_{0}^{2}} (k - R_{0}^{2}) + \lg R_{0}^{2} (58) \end{matrix}$

在不改变单调性和定义域情况下, 用l[k(ρ_p,θ_p,ρ)]近似式(56)中的lg[k(ρ_p,θ_p,ρ)],式(56)化简为:

$\begin{matrix} γ' = - 10 l [k (ρ_{p}, θ_{p}, ρ)] + C (59) \end{matrix}$

可见 γ'是以ρ为参变量、ρ_p和θ_p为自变量的线性函数, 同时它也是二维随机变量, 根据线性函数期望的性质可得:

$\begin{matrix} E [γ'] = - 10 l (E [k (ρ_{p}, θ_{p}, ρ)]) + C (60) \end{matrix}$

其中, $\begin{matrix} E [k (ρ_{p}, θ_{p}, ρ)] 化简为 k (ρ) \end{matrix}$ :

$\begin{matrix} \begin{matrix} k (ρ) = \int_{0}^{2} \int_{R_{0}}^{R} ρ_{p}^{2} - 2 ρ_{p} ρcos θ_{p} + ρ^{2}) \times \\ \frac{1}{2 π (R - R_{0})} d ρ_{p} d θ_{p} = \\ \frac{1}{3} (R^{2} + R R_{0} + R_{0}^{2}) + ρ^{2} (61) \end{matrix} \end{matrix}$

求 $\begin{matrix} k (ρ) \end{matrix}$ 的一阶导数为:

$\begin{matrix} k' (ρ) = 2 ρ \geq 0 (62) \end{matrix}$

由式(62)可得 k(ρ)是ρ的递增函数,而E(γ')是k(ρ)的递减函数,根据复合函数单调性定理可得,E(γ')是ρ的递减函数。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	FCC. Spectrum policy task force report[R]. Washington D C: Federal Communications Commission, 2002. [本文引用:1]
[2]	Islam M H, Koh C L, Oh S W. Spectrum survey in Singapore: occupancy measurements and analysis[C]∥The 3rd International Conference on Cognitive Radio Oriented Wireless Networks and Communications, Singapore, 2008: 1-7. Islam M H, Koh C L, Oh S W. Spectrum survey in Singapore: occupancy measurements and analysis[C]∥The 3rd International Conference on Cognitive Radio Oriented Wireless Networks and Communications, Singapore, 2008: 1-7. [本文引用:1]
[3]	Mitola III J, Jr Maguire G Q. Cognitive radio: making software radios more personal[J]. IEEE Journal on Personal Communications, 1999, 6(4): 13-18. [本文引用:1]
[4]	Zeng Y, Liang Y C, Hoang A T, et al. A review on spectrum sensing for cognitive radio: challenges and solutions[J]. EURASIP Journal on Advances in Signal Processing, 2010, 2010(2): 1-15. [本文引用:1]
[5]	Yucek T, Arslan H. A survey of spectrum sensing algorithms for cognitive radio applications[J]. IEEE Journal on Communications Surveys & Tutorials, 2009, 11(1): 116-130. [本文引用:1]
[6]	Jia P, Vu M, Le-Ngoc T. Capacity-and Bayesian-based cognitive sensing with location side information[J]. IEEE Journal on Selected Areas in Communications, 2011, 29(2): 276-289. [本文引用:1]
[7]	Choi K W, Hossain E, Kim D I. Cooperative spectrum sensing under a rand om geometric primary user network model[J]. IEEE Transactions on Wireless Communications, 2011, 10(6): 1932-1944. [本文引用:1]
[8]	Unnikrishnan J, Veeravalli V V. Cooperative sensing for primary detection in cognitive radio[J]. IEEE Journal of Selected Topics in Signal Processing, 2008, 2(1): 18-27. [本文引用:1]
[9]	Xia H H. A simplified analytical model for predicting path loss in urban and suburban environments[J]. IEEE Transactions on Vehicular Technology, 1997, 46(4): 1040-1046. [本文引用:1]
[10]	Digham F F, Alouini M S, Simon M K. On the energy detection of unknown signals over fading channels[C]∥IEEE International Conference on Communications, Alaska, 2003: 3575-3579. [本文引用:1]
[11]	Peh E, Liang Ying-chang. Optimization for cooperative sensing in cognitive radio networks[C]∥IEEE International Conference on Wireless Communications and Networking, Hong Kong, 2007: 27-32. [本文引用:1]

2002

0.0

... 0 引言频谱感知是认知无线电技术的基础^[1,2,3],具有快速准确的频谱感知能力是对高性能认知无线电设备的基本要求 ...

2008

0.0

... 0 引言频谱感知是认知无线电技术的基础^[1,2,3],具有快速准确的频谱感知能力是对高性能认知无线电设备的基本要求 ...

1999

0.0

... 0 引言频谱感知是认知无线电技术的基础^[1,2,3],具有快速准确的频谱感知能力是对高性能认知无线电设备的基本要求 ...

2010

0.0

... 电磁环境中的多径效应、阴影衰落和噪声不确定性严重影响了系统的频谱感知性能^[4],因此单用户频谱感知有时很难满足认知无线电系统要求 ...

2009

0.0

... 由于协作频谱感知能够大大提高频谱感知性能,因此受到普遍关注^[5] ...

2011

0.0

2011

0.0

2008

0.0

1997

0.0

... 路径损耗值主要由距离、波长、天线高度和环境决定,因为本文主要考查距离对路径损耗的影响,所以采用如下简化的路径损耗模型^[9]: ...

2003

0.0

... 瑞利衰落信道中,接收信号的信噪比是一个随机变量,其概率密度函数为^[10]: ...

2007

0.0

... 准则理论^[11]得到的,第二组的理论值曲线和第三组的理论值曲线重合,说明传统的#cod#x0201c ...