基于不完全信道信息的D2D功率分配算法

引用本文

马蓓, 张海林, 张兆维, 钟鸣. 基于不完全信道信息的D2D功率分配算法.吉林大学学报:工学版, 2016, 46(4): 1320-1324
MA Bei, ZHANG Hai-lin, ZHANG Zhao-wei, ZHONG Ming. Imperfect channel state information based D2D power allocation algorithm. Journal of Jilin University Engineering and Technology Edition, 2016, 46(4): 1320-1324 复制到剪切板

Permissions

基于不完全信道信息的D2D功率分配算法

马蓓, 张海林, 张兆维, 钟鸣

西安电子科技大学综合业务网理论及关键技术国家重点实验室,西安 710071

作者简介:马蓓(1982-),女,博士研究生.研究方向:D2D通信网络资源分配.E-mail:beima@mail.xidian.edu.cn

基金:国家自然科学基金项目(61072069, 61301169)

摘要

针对蜂窝与终端直通(Device-to-device,D2D)混合网络中的不完全信道状态信息(Channel state information, CSI),提出了一种基于不完全CSI的最优功率分配算法。利用拉格朗日乘数法推导出了最优功率分配解的闭式表达式。相对于传统的最大发送功率分配方案,该最优解受信道信息误差的影响较小,具有较好的鲁棒性。仿真结果表明,本文算法可以节约发送功率,并得到更大的接收信噪比。

关键词: 通信技术; 终端直通; 不完全信道状态信息; 功率分配; 鲁棒性

中图分类号:TN915 文献标志码:A 文章编号:1671-5497(2016)04-1320-05

Imperfect channel state information based D2D power allocation algorithm

MA Bei, ZHANG Hai-lin, ZHANG Zhao-wei, ZHONG Ming

State Key Laboratory of Integrated Services Networks, Xidian University, Xi'an 710071, China

Abstract

An optimal power allocation algorithm is developed for cellular and Device-to-Device (D2D) hybrid network, where the Channel State Information (CSI) is imperfect. The obtained power solution is a simple but solid closed-form using the Lagrange multiplier method. The proposed power allocation algorithm is more robust to the CSI as compared with the traditional maximum transmit power allocation scheme. Simulation results show that the proposed algorithm can obtain higher received Signal-to-Noise Ratio (SNR) than that obtained using traditional power allocation scheme.

Keyword: communications; device-to-detive(D2D); imperfect channel state information; power allocation; robustness

Show Figures

0 引言

终端直通(Device-to-device, D2D)通信具有降低终端发射功率、提高网络吞吐量、瞬时数据速率以及系统频谱效率等诸多优势, 最近几年得到了越来越多的关注^{[1, 2, 3]}。功率分配是影响D2D通信系统性能的重要因素, 因此成为研究的基本问题。文献[4]提出了一种功率与资源块的联合优化分配算法, 在优化D2D链路总速率的同时保证了蜂窝用户的服务质量。文献[5]在总传输速率受限的情况, 研究了网络功率消耗最小化的功率分配方法。文献[6]提出了一种LTE网络中D2D贪婪功率分配方案, 提高了D2D系统的吞吐量。文献[7]设计了一种子区间最优值搜索算法, 分析了蜂窝与D2D混合网络中多频带资源的场景下D2D用户最佳密度和功率分配问题。文献[8]提出了一种基于中继的资源分配方案, 实现了次级用户在两个时隙内的双向通信。然而, 这些研究工作都是基于完全信道状态信息(Channel state information, CSI), 而忽略了实际网络中不完全CSI对系统性能的影响。

因此, 在现实场景中分析不完全CSI对D2D功率分配问题的影响有重要的意义。本文提出了一种具有鲁棒性的最优功率分配算法。构造以蜂窝基站的接收信噪比最大为目标的凸优化问题, 并利用Karush-Kuhu-Tucker(KKT)条件得出了最优功率分配的闭式解。最优功率分配的D2D用户作为中继帮助蜂窝用户完成传统的蜂窝通信, 提高蜂窝网络系统的频谱效率和网络容量。仿真结果表明, 该功率分配算法受信道信息误差的影响较传统的最大发送功率分配方案小, 在同等误差条件下, 接收信噪比性能得到改善。

1 系统模型

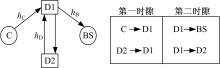
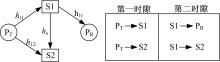
研究蜂窝系统中D2D作为中继的通信场景, 如图1所示。为了简化分析, 研究的网络模型为单蜂窝小区。网络节点包含一个蜂窝用户C、一对D2D用户(D1, D2)以及一个蜂窝基站BS。在时分双工模式下, D2D用户对(D1, D2)共享蜂窝用户C的上行信道资源建立本地直连通信。同时, D2D用户D1作为中继帮助蜂窝用户C完成其与基站BS间的通信。用h_C、h_B和h_D分别表示C→ D1、D1→ BS和D2→ D1链路的信道衰落系数。假设节点BS、C、D1和D2的发送信号均服从均值为0、方差为1的高斯分布。用P_C、P_D和 $\begin{matrix} P_{2} \end{matrix}$ 分别表示C、D1和D2的发送功率。不失一般性, 假设节点BS、D1和D2处的噪声分别为独立的均值为0、方差为 $\begin{matrix} σ_{i}^{2} (i = n_{B}, n_{D}, 2) \end{matrix}$ 的加性高斯白噪声。

	Figure Option View Download New Window
	图1 系统模型Fig.1 System model

由于在实际的蜂窝通信场景中存在着信道估计误差, C→ D1和D1→ BS链路的信道模型可表示为:

$\begin{matrix} \begin{matrix} h_{C} = {\hat{h}}_{C} + e_{C} \end{matrix} \end{matrix}$ (1)

$\begin{matrix} h_{B} = {\hat{h}}_{B} + e_{B} \end{matrix}$ (2)

式中: $\begin{matrix} {\hat{h}}_{C} \end{matrix}$ 和 $\begin{matrix} {\hat{h}}_{B} \end{matrix}$ 表示信道 $\begin{matrix} h_{C} \end{matrix}$ 和 $\begin{matrix} h_{B} \end{matrix}$ 的最小均方误差估计; $\begin{matrix} e_{C} \end{matrix}$ 和 $\begin{matrix} e_{B} \end{matrix}$ 表示相应的信道估计误差, 且分别服从复正态分布 $\begin{matrix} CN (0, σ_{e_{C}}^{2}) \end{matrix}$ 和 $\begin{matrix} CN (0, σ_{e_{B}}^{2}) 。 \end{matrix}$ 信道估计误差的方差 $\begin{matrix} σ_{e_{C}}^{2} \end{matrix}$ 和 $\begin{matrix} σ_{e_{B}}^{2} \end{matrix}$ 与相应的信道估计 $\begin{matrix} {\hat{h}}_{C} \end{matrix}$ 和 $\begin{matrix} {\hat{h}}_{B} \end{matrix}$ 是不相关的。

传输过程分为两个时隙。第一时隙, 节点C向中继D1发送信号, 同时节点D2也向中继D1发送信号。中继D1接收到的信号 $\begin{matrix} x_{D} \end{matrix}$ 可表示为:

$\begin{matrix} x_{D} = \sqrt[]{P_{C}} {\hat{h}}_{C} s + \sqrt[]{P_{C}} e_{C} s + \sqrt[]{P_{2}} h_{D} s_{2} + n_{D} \end{matrix}$ (3)

式中: $\begin{matrix} s \end{matrix}$ 和 $\begin{matrix} P_{C} \end{matrix}$ 分别表示节点C的发送信号和发送功率; $\begin{matrix} s_{2} \end{matrix}$ 和 $\begin{matrix} P_{2} \end{matrix}$ 分别表示节点D2的发送信号和发送功率; $\begin{matrix} n_{D} \end{matrix}$ 是中继D1处的均值为0、方差为 $\begin{matrix} σ_{n_{D}}^{2} \end{matrix}$ 的复高斯随机噪声。

由于节点D1是信号 $\begin{matrix} s_{2} \end{matrix}$ 的目的节点, 通过将来自节点C的信号当作噪声处理, 可以首先解出信号 $\begin{matrix} s_{2} 。 \end{matrix}$ 为了保证成功解调, D2→ D1链路的可达传输速率为:

$\begin{matrix} R_{21} (P_{2}, P_{C}) = \frac{1}{2} lo g_{2} (1 + \frac{g_{s} P_{2}}{g_{c} P_{C} + σ_{n_{D}}^{2}}) \end{matrix}$ (4)

式(4)对D2→ D1链路的带宽进行了归一。其中, “ 1/2” 表示该传输占用了一半的协议规定的通信时间。 $\begin{matrix} g_{s} \end{matrix}$ 和 $\begin{matrix} g_{c} \end{matrix}$ 分别表示信道 $\begin{matrix} h_{D} \end{matrix}$ 和 $\begin{matrix} h_{C} \end{matrix}$ 的信道功率增益, $\begin{matrix} g_{c} = {|h_{C}|}^{2}, g_{s} = {|h_{D}|}^{2} 。 \end{matrix}$ 在成功解出信号 $\begin{matrix} s_{2} \end{matrix}$ 后, 中继D1将 $\begin{matrix} s_{2} \end{matrix}$ 从接收信号 $\begin{matrix} x_{D} \end{matrix}$ 中去除。则中继D1的接收信号变为:

$\begin{matrix} y_{CD} = \sqrt[]{P_{C}} {\hat{h}}_{C} s + \sqrt[]{P_{C}} e_{C} s + n_{D} \end{matrix}$ (5)

第二时隙, 节点D1采用放大-转发中继模式转发信号 $\begin{matrix} y_{CD}, \end{matrix}$ 同时向节点D2发送自己的信号进行D2D通信。节点BS通过将发送给D2的信息当作噪声处理, 可以解出其期望信号。节点BS处的接收信号 $\begin{matrix} y_{B} \end{matrix}$ 可表示为:

$\begin{matrix} y_{B} = β (\sqrt[]{P_{C}} {\hat{h}}_{C} s + \sqrt[]{P_{C}} e_{C} s + n_{D}) ({\hat{h}}_{B} + e_{B}) + n_{B} \end{matrix}$ (6)

式中: $\begin{matrix} β = \sqrt[]{\frac{P_{D}}{P_{C} ({|{\hat{h}}_{B}|}^{2} + σ_{e_{B}}^{2}) + σ_{n_{D}}^{2}}} \end{matrix}$ 是放大系数, 保证了中继节点D1的发送功率为 $\begin{matrix} P_{D}; n_{B} \end{matrix}$ 是节点BS处的均值为0、方差为 $\begin{matrix} σ_{n_{B}}^{2} \end{matrix}$ 的复高斯随机噪声。通过将信道估计误差当作加性噪声, 节点BS的接收信噪比可以表示为:

$\begin{matrix} \begin{matrix} r = ψ_{1} ψ_{2} P_{C} P_{D} / {[(ψ_{1} + ψ_{2} + 1) P_{C} P_{D} + \\ (ψ_{1} + 1) ψ_{4} P_{C} + (ψ_{2} + 1) ψ_{3} P_{D} + ψ_{3} ψ_{4}]} \end{matrix} \end{matrix}$ (7)

式中: $\begin{matrix} ψ_{1} = {|{\hat{h}}_{C}|}^{2} / σ_{e_{C}}^{2}; ψ_{2} = {|{\hat{h}}_{B}|}^{2} / σ_{e_{B}}^{2}; ψ_{3} = σ_{n_{D}}^{2} / σ_{e_{C}}^{2}; ψ_{4} = σ_{n_{B}}^{2} / σ_{e_{B}}^{2} 。 \end{matrix}$

综上可以看出, 信道估计误差对基站端的接收信噪比有重要的影响。

2 功率分配

依据接收信噪比最大准则, 分析不完全信道状态信息下蜂窝节点C和D2D中继节点D1最优功率分配的问题。优化问题(P1)可描述为:

$\begin{matrix} \begin{matrix} \min 1 / r (8) \\ s . t . \begin{matrix} P_{C} + P_{D} \leq P_{T} (9) \\ P_{C} \geq 0, P_{D} T \geq 0 (10) \\ \frac{1}{r} \leq \frac{1}{r_{\min}} (11) \end{matrix} \end{matrix} \end{matrix}$

式中: $\begin{matrix} P_{T} \end{matrix}$ 是协作传输中的最大总功率; $\begin{matrix} r_{\min} \end{matrix}$ 是节点BS接收信噪比的门限值。第一个约束条件(式(9))是协作传输中总功率一定的约束条件。第二个约束条件(式(10))保证了分配功率的非负性。第三个约束条件(式(11))保证了接收信噪比满足门限值 $\begin{matrix} r_{\min} 。 \end{matrix}$ 在优化问题P1中, 约束条件(9)和(10)是线性的。因此, P1是一个凸优化问题。通过拉格朗日乘数法可以得出P1的最优解。

定理1 在不完全CSI下, 最优功率分配问题P1的最优解可以表示为:

$\begin{matrix} \begin{matrix} P_{C}^{*} = \\ \frac{\sqrt[]{({|{\hat{h}}_{C}|}^{2} + σ_{e_{C}}^{2}) P_{T} + 1} P_{T}}{\sqrt[]{({|{\hat{h}}_{C}|}^{2} + σ_{e_{C}}^{2}) P_{T} + 1} + \sqrt[]{({|{\hat{h}}_{B}|}^{2} + σ_{e_{B}}^{2}) P_{T} + 1}} (12) \\ P_{D}^{*} = \\ \frac{\sqrt[]{({|{\hat{h}}_{B}|}^{2} + σ_{e_{B}}^{2}) P_{T} + 1} P_{T}}{\sqrt[]{({|{\hat{h}}_{C}|}^{2} + σ_{e_{C}}^{2}) P_{T} + 1} + \sqrt[]{({|{\hat{h}}_{B}|}^{2} + σ_{e_{B}}^{2}) P_{T} + 1}} (13) \end{matrix} \end{matrix}$

证明引入约束条件(9)(10)和(11)对应的非负拉格朗日乘子 $\begin{matrix} λ_{i}, i = 1, 2, 3, 4, \end{matrix}$ 优化问题P1可描述为:

$\begin{matrix} \begin{matrix} L (P_{C}, P_{D}, λ_{i}) = λ_{1} (P_{C} + P_{D} - P_{T}) + λ_{2} (- P_{C}) + \\ λ_{3} (- P_{D}) + λ_{4} (\frac{1}{r} - \frac{1}{r_{\min}}) + \frac{1}{r} (14) \end{matrix} \end{matrix}$

优化问题P1的KKT条件可以表示为:

$\begin{matrix} \begin{matrix} \frac{\partial L (P_{C}, P_{D}, λ_{i})}{\partial P_{C}^{*}} = - (λ_{4}^{*} + 1) \times \\ \frac{ψ_{4} [(1 + ψ_{1}) P_{D}^{*} + ψ_{3}]}{ψ_{1} ψ_{2} P_{C}^{* 2} P_{D}^{*}} + \\ λ_{1}^{*} - λ_{2}^{*} = 0 (15) \\ \frac{\partial L (P_{C}, P_{D}, λ_{i})}{\partial P_{D}^{*}} = - (λ_{4}^{*} + 1) \times \\ \frac{ψ_{3} [(1 + ψ_{2}) P_{C}^{*} + ψ_{4}]}{ψ_{1} ψ_{2} P_{C}^{*} P_{D}^{* 2}} + \\ λ_{1}^{*} - λ_{3}^{*} = 0 (16) \\ λ_{1}^{*} (P_{C}^{*} + P_{D}^{*} - P_{T}) = 0 (17) \\ λ_{2}^{*} (- P_{C}^{*}) = 0 (18) \\ λ_{3}^{*} (- P_{D}^{*}) = 0 (19) \\ λ_{4}^{*} (\frac{1}{r} - \frac{1}{r_{\min}}) = 0 (20) \\ - P_{C}^{*} \leq 0 (21) \\ - P_{D}^{*} \leq 0 (22) \\ \frac{1}{r} - \frac{1}{r_{\min}} \leq 0 (23) \\ P_{C}^{*} + P_{D}^{*} - P_{T} \leq 0 (24) \\ λ_{i}^{*} \geq 0, i = 1, 2, 3, 4 (25) \end{matrix} \end{matrix}$

式中: $\begin{matrix} {(\cdot)}^{*} \end{matrix}$ 表示变量在最优点处的取值。式(17)中, $\begin{matrix} λ_{1}^{*} \end{matrix}$ 与 $\begin{matrix} (P_{C}^{*} + P_{D}^{*} - P_{T}) \end{matrix}$ 不同时为0。类似, 通过讨论式(18)(19)和(20)中 $\begin{matrix} λ_{i}^{*} (i = 2, 3, 4) \end{matrix}$ 的不同取值情况, 可以解上面的KKT条件。因此, 可以得到优化问题P1的最优解 $\begin{matrix} P_{C}^{*} \end{matrix}$ 和 $\begin{matrix} P_{D}^{*}, \end{matrix}$ 如式(12)(13)所示。

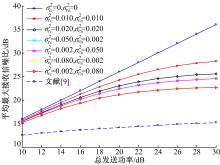
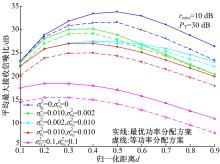
综上可以看出, 蜂窝节点C和D2D中继节点D1的最优功率解 $\begin{matrix} P_{C}^{*} \end{matrix}$ 和 $\begin{matrix} P_{D}^{*} \end{matrix}$ 均受到信道估计误差的影响。所得最优解满足约束条件(9)(10)和(11)。

3 仿真结果

对本文提出的功率分配算法(定理1)进行了性能仿真。仿真参数如下:蜂窝小区半径为500 m; D2D对距离为25 m; D1与BS间的距离为250 m; 路径损耗系数为4; 基站接收信噪比门限值r_min=10 dB; 节点D1和BS端的噪声功率 $\begin{matrix} σ_{n_{D}}^{2} = σ_{n_{B}}^{2} = 1; \end{matrix}$ 最大总发送功率P_T=30 dB。作为比较, 文献[9]的系统模型如图2所示。

	Figure Option View Download New Window
	图2 文献[9]系统模型Fig.2 System model of Ref.[9]

	Figure Option View Download New Window
	图3 不同信道估计误差下的平均最大接收信噪比Fig.3 Average maximal received SNR with different channel estimation errors

图3给出了在各种信道估计误差取值情况下, 平均最大接收信噪比随发送功率变化的仿真结果。可以看出, 平均最大接收信噪比随着发送功率的增加而增大。对于给定的发送功率, 最大接收信噪比随信道估计误差的增加而减小。当误差较大且不平衡时, 平均最大接收信噪比增加的趋势呈减弱状态。这里, 估计误差的不平衡是指信道C→ D1与D1→ BS的误差方差不相等的情况, 即 $\begin{matrix} σ_{e_{C}}^{2} \neq σ_{e_{B}}^{2} 。 \end{matrix}$ 当两条不平衡曲线对称时, 例如, $\begin{matrix} (σ_{e_{C}}^{2}, σ_{e_{B}}^{2}) \end{matrix}$ 取值分别为(0.050, 0.002)和(0.002, 0.050)时, 这两条对称曲线将对应相同的最大接收信噪比。

首先, 与文献[9]的单向通信相比, 本文所提协议实现了D2D用户在两个时隙内的双向通信, 同时保证了更大的接收信噪比性能。这是因为, 在本文所提出的协议模型中, 中继节点D1在第一时隙将来自节点D2的信号解码, 并在第二时隙将其从中继信号中去除。因此, 对于蜂窝用户C来说, 第二时隙的信号处理与文献[9]是一样的, 即D2D用户的双向通信并不影响蜂窝用户的系统性能。其次, 由于节点D2可以在第一时隙复用蜂窝用户的上行资源, 提高了频谱利用率。而且, 性能的提高不仅来自于协议所允许的传输本身, 还来自于所提出的最优功率分配方案。相比之下, 在文献[9]中, 蜂窝用户只能固定使用其最大发送功率。

图4给出了各种信道估计误差情况下平均最大接收信噪比随蜂窝用户位置信息变化的仿真曲线。作为比较, 图中也给出了采用等功率分配方案的性能曲线。可以看出, 对于所有的信道估计误差, 本文所提出的功率分配算法优于等功率分配方案。图4显示, $\begin{matrix} d \end{matrix}$ 的取值随信道估计误差的增大而减小。当信道估计误差为零时(即 $\begin{matrix} σ_{e_{C}^{}}^{2} = σ_{e_{B}^{}}^{2} = 0), \end{matrix}$ 且中继节点D1位于蜂窝用户C和基站BS的中间位置时(即 $\begin{matrix} d = 0.5), \end{matrix}$ 平均最大接收信噪比可以获得最大值。当信道估计误差对称时, 例如, 误差方差 $\begin{matrix} (σ_{e_{C}}^{2}, σ_{e_{B}}^{2}) \end{matrix}$ 取值为(0.01, 0.002)和(0.002, 0.01)时, 最佳D2D位置为 $\begin{matrix} d = 0.4, \end{matrix}$ 此时平均最大接收信噪比达到最大值。

	Figure Option View Download New Window
	图4 平均最大接收信噪比随蜂窝用户位置的变化曲线Fig.4 Curve of average maximal received SNR versus location of cellular user

4 结束语

研究了不完全CSI对D2D通信最优功率分配的影响。给出以接收信噪比最大化为目标的功率分配最优解。仿真结果证明:本文算法受信道估计误差的影响较传统的最大发送功率分配方案小, 具有较好的鲁棒性。同时证明了考虑信道估计误差对最优功率分配方案设计的重要性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	崔鹏, 陈力. D2D 技术在LTE-A系统中的应用[J]. 现代电信科技, 2011, 2(1) : 92-95. Cui Peng, Chen Li. Applications of device-to-device in LTE-A system[J]. Modern Science & Technology of Telecommunications, 2011, 2(1): 92-95. [本文引用:1]
[2]	Lei L, Zhong Z, Lin C, et al. Operator controlled device-to-device communications in LTE-advanced networks[J]. IEEE Wireless Communications, 2012, 19(3): 96-104. [本文引用:1]
[3]	The 3rd Generation Partnership Project, Release 12, Tech Rep 3GPP TR 22. 803 V12. 2. 0, Technical specification group services and system aspects: feasibility study for proximity service (ProSe)he 3rd Generation Partnership Project, Release 12, Tech Rep 3GPP TR 22. 803 V12. 2. 0, Technical specification group services and system aspects: feasibility study for proximity service (ProSe)[S]. 2013. [本文引用:1]
[4]	Tirkkonen C H, Doppler K, Ribeiro C. Power optimization of device-to-device communication underlaying cellular communication[C]∥IEEE International Conference on Communications, Dresden, Germany, 2009: 1-5. [本文引用:1]
[5]	Fodor G, Reider N. A distributed power control scheme for cellular network assisted D2D communications[C]∥IEEE GLOBECOM, Houston, TX, USA, 2011: 1-6. [本文引用:1]
[6]	荣涛, 吴斌, 糜正琨. 一种LTE 网络D2D通信资源共享算法[J]. 南京邮电大学学报: 自然科学版, 2013, 33(3) : 85-90. Rong Tao, Wu Bin, Mi Zheng-kun. Resource sharing algorithm for D2D communications in LTE-A network[J]. Journal of Nanjing University of Posts and Telecommunications (Natural Science), 2013, 33(3) : 85-90. [本文引用:1]
[7]	胡春静, 刘子扬, 彭博, 等. 多频带混合场景下终端直通通信用户最优用户密度与功率分配研究[J]. 电子与信息学报, 2014, 36(5): 1171-1177. Hu Chun-jing, Liu Zi-yang, Peng Bo, et al. Optimal user density and power allocation in D2D multi-band hybrid scenario[J]. Journal of Electronics and Information Technology, 2014, 36(5): 1171-1177. [本文引用:1]
[8]	Pei Yi-yang, Liang Ying-chang. Cooperative spectrum sharing with bidirectional secondary transmission[J]. IEEE Transaction on Vehicular Technology, 2015, 64(1): 108-117. [本文引用:1]
[9]	Han Y, Pand haripand e A, Ting S. Cooperative spectrum sharing via controlled amplify-and -forward relaying[C]∥IEEE PIMRC, Cannes, FRA, 2008: 1-5. [本文引用:1]

2011

0.0

... 0 引言终端直通(Device-to-device,D2D)通信具有降低终端发射功率、提高网络吞吐量、瞬时数据速率以及系统频谱效率等诸多优势,最近几年得到了越来越多的关注^[1,2,3] ...

2012

0.0

2013

0.0

2009

0.0

2011

0.0

2013

0.0

. 2013, 33(3):85-90 DOI:doi:10.3969/j.issn.1673-5439.2013.03.013

Resource sharing algorithm for D2D communications in LTE-A network

一种LTE 网络D2D通信资源共享算法

Rong Tao , Wu Bin , Mi Zheng-kun.

荣涛, 吴斌, 糜正琨

Device�to�Device communication can effectively reduce the load of eNodeB in LTE networks.However，while sharing radio resources between D2D and cellular systems，there will be interference between systems.It can be effectively alleviated with reasonable resource allocation.A greedy resource allocation algorithm is proposed for D2D with LTE networks.It can guarantee the cellular system exempt from the D2D interference while a D2D pair sharing resources of multiple cellular users to increase the throughput of D2D system.The simulation results have shown the performance comparison between the proposed algorithm，random allocation algorithm and interference�aware resouce allocation algorithm.

在LTE网络下部署D2D（Device?to?Device）系统能有效降低基站的负荷，但是D2D系统共享蜂窝系统资源时会产生系统间干扰，通过合理的资源分配可以有效降低这种干扰。文中提出一种LTE网络中D2D贪婪资源分配算法，该算法能保证蜂窝系统不受D2D通信的干扰影响，同时单个D2D对可以复用多个蜂窝用户资源，以提高D2D系统的吞吐量。最后通过仿真给出本算法与随机分配和干扰感知分配算法的性能比较。

2014

0.0

. 2014, 36(5):1171-1177 DOI:doi:10.3724/SP.J.1146.2013.01023

Optimal user density and power allocation in D2D multi-band hybrid scenario

多频带混合场景下终端直通通信用户最优用户密度与功率分配研究

Hu Chun-jing , Liu Zi-yang , Peng Bo

胡春静, 刘子扬, 彭博

This paper analyzes the optimal density and power allocation for the D2D (Device-to-Device) communication in heterogeneous networks on multi-bands with target of maximizing the D2D transmission capacity. The heterogeneous networks contain one or several cellular systems, and the D2D communication shares uplink resources with them. By utilizing stochastic geometry, it is formed as a sum capacity optimization problem for the D2D network with constraints that guarantee outage probabilities of both cellular and the D2D transmissions. Since the original problem is non-convex, the proof work is divided into two steps: first, it is proved that the power allocation problem is convex when the D2D density is fixed, which can be solved by Lagrangian method; and then that the feasible region for the D2D user density is divided into finite sub-intervals by the outage constraints and the local maximum D2D transmission capacity can be obtained by the derivative method. A sub-interval linear searching algorithm based on the above conclusions is proposed. The simulation results demonstrate the effectiveness of the proposed algorithm and show that the optimal parameters of the D2D transmission is mainly affected by the outage constraints and the interference from cellular systems.

该文分析了蜂窝与终端直通(Device-to-Device, D2D)混合网络中多频带资源的场景下D2D用户最佳密度和功率分配问题。在混合网络中包含一个或者多个蜂窝网络，D2D用户复用蜂窝系统上行频谱资源。通过采用随机几何理论，上述问题可以建模成一个以最大化D2D网络容量为目标并以蜂窝用户和D2D用户的中断概率为约束条件的优化问题。由于上述优化问题非凸，因此分成两步解决原问题：首先证明当D2D用户密度确定的时候原问题对于功率分配是凸问题，并通过拉格朗日对偶方法得到了最优功率分配方案；随后证明中断约束条件将D2D用户密度的定义域分成有限个子区间，在每个子区间上可以通过求导的方式得到D2D传输容量局部最优解，基于上述两个结论，文中设计了一种子区间最优值搜索算法。通过仿真验证了算法的有效性，并且反映出D2D传输容量主要由中断约束条件和来自蜂窝网络的干扰决定。

2015

0.0

2008

0.0