基于帧间差分和背景差分的运动目标检测算法

引用本文

孙挺, 齐迎春, 耿国华. 基于帧间差分和背景差分的运动目标检测算法.吉林大学学报:工学版, 2016, 46(4): 1325-1329
SUN Ting, QI Ying-chun, GENG Guo-hua. Moving object detection algorithm based on frame difference and background subtraction. Journal of Jilin University Engineering and Technology Edition, 2016, 46(4): 1325-1329 复制到剪切板

Permissions

基于帧间差分和背景差分的运动目标检测算法

孙挺^1,², 齐迎春², 耿国华¹

1.西北大学可视化研究所,西安 710069

2.周口师范学院计算机科学与技术学院,河南周口 466001

作者简介:孙挺(1972-),男,副教授,博士.研究方向:智能信息处理,科学可视化.E-mail:20011026@zknu.edu.cn

基金:“973”国家重点基础研究发展计划前期研究专项项目(2011CB311802); 河南省科技厅科技发展计划项目(122400450356); 河南省科技厅科技发展计划软科学项目(132400410927)

摘要

针对运动目标检测领域中帧间差分法和背景差分法的缺陷,提出一种将两种方法融合在一起的新算法。首先,该算法在采用混合高斯建立背景模型时对方差更新作了修改,使得模型与真实背景更接近。其次,用连续三帧差分代替两帧差分,采取自适应差分阈值的方法。最后,将两种差分的结果融合并作形态学处理提取目标。实验结果表明,本文算法能有效抑制噪声和空洞,适应性强、检测效果良好。

关键词: 通信技术; 帧间差分; 背景差分; 目标检测; 融合

中图分类号:TN91 文献标志码:A 文章编号:1671-5497(2016)04-1325-05

Moving object detection algorithm based on frame difference and background subtraction

SUN Ting^1,², QI Ying-chun², GENG Guo-hua¹

1.Institute of Visualization Technology,Northwest University,Xi'an 710069,China

2.School of Computer Science and Technology,Zhoukou Normal University,Zhoukou 466001,China

Abstract

In order to overcome the defects of frame difference and background subtraction algorithms in moving object detection, a new method that integrates the two algorithms is proposed. First, when the Gaussian mixture model is employed to build the background model, the update of the variance is modified, so the model is more close to the real background. Then, two consecutive frame differencing is replaced by three consecutive frame differencing, and the differencing threshold is adaptive. Finally, the results of the two differences are integrated and the target is extracted after morphological process. Experimental results show that the method can effectively suppress noise and the "hole", the method is more adaptable and has good detection results.

Keyword: communications; frame difference; background subtraction; object detection; integration

Show Figures

0 引言

运动目标检测算法包括背景差分法^{[1, 2]}、帧间差分法^{[3, 4]}和光流法^{[5, 6]}等。光流法算法复杂、需要特殊的硬件支持、实时性较差。背景差分法是将当前帧与背景模型进行差分操作来实现对运动目标的检测, 该算法准确性高、易于实现、检测速度快, 但是由于实际场景的复杂多变, 而且存在着各种噪声和干扰, 造成背景建模和模拟的难度增加。文献[7]提出用混合高斯模型(Gaussian mixture model, GMM)建立背景, 有效解决了背景的干扰问题, 文献[8]在GMM算法的基础上, 利用支持向量机对前景像素作进一步判断, 减少了复杂环境下检测的错误率。帧间差分法是将相邻连续两帧或者三帧图像进行差分来获得运动目标轮廓, 该算法时间复杂度较低, 因此是运动目标检测中使用较多的一种算法, 但当较大的噪声出现在视频图像序列中时, 该算法的性能会明显下降, 检测错误率增加, 且该方法对噪声的变化比较敏感, 而且要求目标的运动速度不能过快。当目标表面灰度大面积均匀时, 会产生空洞现象, 使目标被分割成多个区域。文献[9]提出一种结合光流法与三帧差分法的运动目标检测算法, 选择图像中具有代表性的Harris角点像素计算光流信息, 简化了光流的计算, 引入三帧差分法作为简化光流法的补充, 但光流算法较复杂。文献[10]提出基于背景建模与帧间差分的目标检测改进算法, 能改善混合高斯背景差分法中高斯背景建模产生的鬼影, 以及帧间差分法的前景检测结果中出现的严重拖影和空洞现象, 并且在背景突变的情况下也能进行有效检测, 但是对过于复杂的运动情况的检测还不是很理想。

背景差分法和帧间差分法运用较为广泛, 但是其优缺点都比较突出, 使用单一的背景差分或帧间差分法的检测效果并不好。因此, 本文将背景差分法与帧间差分法结合起来, 对背景模型中方差的更新作了改进, 用连续三帧差分代替两帧差分, 并使用自适应的阈值。通过上述步骤, 本文算法能较好地检测运动目标并具有较强的鲁棒性。

1 背景建模及背景差分

1.1 背景建模

背景差分的关键在于背景建模, 基于高斯混合模型的背景建模是现在常用的算法。单一分布的高斯模型能较好地适用于室内场景; 但是在环境变化较复杂的室外, 单高斯分布^[11]的模型会出现较大偏差, 容易将晃动的树叶、喷泉等背景误认为前景。因此, 本文采用混合高斯模型算法^[12]来进行背景建模, 能较好地处理背景混乱和光线突然变化等干扰。

图像中某像素点p(x₀,y₀ ),假设它在1~t时刻的像素值为(x_l,…x_i,…x_t )。对这些像素值使用k个高斯分布来进行描述,则x_t 的概率密度函数由k个高斯分布的加权混合表示如下^[13]:

$\begin{matrix} p (x_{t}) = \overset{k}{\sum_{i = 1}} w_{t, i} \cdot η (x_{t}, u_{t, i}, Σ_{t, i}) (1) \end{matrix}$

式中: $\begin{matrix} w_{t, i} 、 u_{t, i} 和 Σ_{t, i} 分别为 t 时刻混合高斯模型第 i \end{matrix}$ 个高斯分布的权重( $\begin{matrix} \overset{k}{\sum_{i = 1}} \end{matrix}$ w_t_,_i=1)、均值和协方差矩阵; $\begin{matrix} η (x_{t}, u_{t, i}, Σ_{t, i}) \end{matrix}$ 为高斯分布的概率密度函数:

$\begin{matrix} \begin{matrix} η (x_{t}, u_{t, i}, Σ_{t, i}) = \frac{1}{{(2 π)}^{n / 2} {|Σ_{t, i}|}^{\frac{1}{2}}} \cdot \\ e^{- \frac{1}{2} (x_{t} - u_{t, i})^{T} Σ_{t, i}^{- 1} (x_{t} - u_{t, i})} (2) \end{matrix} \end{matrix}$

当t+1时刻的观测点到来时,将x_t+1分别与k个高斯分布的均值u_t,_i做比较。并按某一判断规则选择匹配的高斯分布。这个规则为:

$\begin{matrix} | x_{t + 1} - u_{t, i} |< c \cdot σ_{t, i}^{2}, i = 1, 2, \dots, k (3) \end{matrix}$

式中: $\begin{matrix} c \end{matrix}$ 为自定义参数, 在实际应用中一般取2.5。若满足上述规则, 则认为 $\begin{matrix} x_{t + 1} 与第 i \end{matrix}$ 个高斯函数匹配。

与 $\begin{matrix} x_{t} \end{matrix}$ 相匹配的的高斯分布的参数按如下公式^[14]进行更新:

$\begin{matrix} \begin{matrix} μ_{t, i} & = (1 - ρ) \cdot μ_{t - 1, i} + ρ \cdot x_{t} (4) \\ σ_{t, i}^{2} & = (1 - ρ) \cdot σ_{t, i}^{2} + ρ \cdot (x_{t} - μ_{t, i})^{2} (5) \\ ρ & = α \cdot w_{t, i} (6) \end{matrix} \end{matrix}$

式中:α为高斯分布权值的更新速率(又叫用户定义的学习率),其取值范围为α∈[0,1];ρ为参数的更新速率(又叫参数学习率)。

对于没有匹配的高斯分布, 其均值、方差均保持不变。 $\begin{matrix} k \end{matrix}$ 个高斯分布的权重按如下公式进行更新:

$\begin{matrix} w_{t, i} = (1 - α) \cdot w_{t - 1, i} + α \cdot M (7) \end{matrix}$

对于匹配的第 $\begin{matrix} i 个分布, 取 M = 1; 其余的 k - 1 个分布取 M = 0 。 \end{matrix}$

为提高背景模型的可靠程度, 将权重进行归一化处理, 即 $\begin{matrix} {\tilde{w}}_{t, i} \end{matrix}$ =w_t_,_i/ $\begin{matrix} \overset{k}{\sum_{i = 1}} \end{matrix}$ w_t_,_i。按照比值 $\begin{matrix} {\tilde{w}}_{t, i} / σ_{t, i} \end{matrix}$ 的大小对各分布进行降序排列, 取优先级较高的前b个分布作为可靠背景分布,其中 $\begin{matrix} b = \underset{b'}{\arg \min} \end{matrix}$ ( $\begin{matrix} \overset{b'}{\sum_{i = 1}} \end{matrix} \begin{matrix} {\tilde{w}}_{t, i} \end{matrix}$ > T₁), T₁用来控制背景分布的个数。

在灰度图像中, 每个像素的值为[0, 255], 较暗区域处的像素值只能为0, 较亮区域处的像素值只能为255。而式(5)描述的 $\begin{matrix} σ^{2} 的更新是一个逐渐递减的过程, 最后趋于 0, 这就导致按 {\tilde{w}}_{t, i} / σ_{t, i} 的大小对各分步排序时, σ^{2} = 0 \end{matrix}$ 的分步始终排在前列, 造成背景模型与实际有偏差。因此, 本文给 $\begin{matrix} σ^{2} 设定了一个下限 σ_{\min}^{2}, 取 σ_{\min}^{2} \end{matrix}$ 为初始值的20%, 有:

$\begin{matrix} σ_{t, i}^{2} = \{\begin{matrix} σ_{t, i}^{2}, σ_{t, i}^{2} > σ_{\min}^{2} \\ σ_{\min}^{2}, 其他 \end{matrix} (8) \end{matrix}$

1.2 背景差分

背景差分法是将当前帧与背景模型进行差分操作来实现对运动目标的检测。在建立好背景模型 $\begin{matrix} f_{b} \end{matrix}$ 后, 对当前的每一帧图像 $\begin{matrix} f_{k}, \end{matrix}$ 利用式(9)得到差分图像, 然后按式(10)对差分图像进行二值化, 再对二值图像做一个形态学处理就可以提取运动目标了。

当背景建模完成后, 可按式(9)和式(10)进行背景差分, 得到背景差分后的二值图像Z_k(x, y)。

$\begin{matrix} \begin{matrix} D_{k} (x, y) & = |f_{k} (x, y) - f_{b} (x, y)| (9) \\ Z_{k} (x, y) & = \{\begin{matrix} 0, D_{k} (x, y) < T_{2} \\ 1, D_{k} (x, y) \geq T_{2} \end{matrix} (10) \end{matrix} \end{matrix}$

式中:D_k (x,y)是背景差分图像;Z_k (x,y)是二值图像;T₂为分割阈值。

若帧间差分图像中的某点的像素值小于阈值T₂,则认为该点是静止的,该点被判为背景点;若大于阈值T₂,则认为该点是运动的, 该点被判为目标点。

2 帧间差分

帧间差分法是将相邻连续两帧或者三帧图像进行差分来获得运动目标轮廓。差分公式如下:

$\begin{matrix} \begin{matrix} P_{k} (x, y) = |f_{k} (x, y) - f_{k - 1} (x, y)| (11) \\ R_{k} (x, y) = \{\begin{matrix} 0, D_{k} (x, y) < T_{3} \\ 1, D_{k} (x, y) \geq T_{3} \end{matrix} (12) \end{matrix} \end{matrix}$

式中:P_k (x,y)是帧间差分图像;R_k (x,y)是二值图像;T₃为分割阈值。

若帧间差分图像中的某点的像素值小于阈值T₃, 则认为该点是静止的, 该点被判为背景点; 若大于阈值T₃, 则认为该点是运动的, 该点被判为目标点。

用连续两帧进行差分, 可能存在以下缺点:①检测出的目标包含两帧中变化的信息, 存在较多的目标点, 检侧出来的目标比实际目标范围要大, 甚至出现“ 双影” 现象; ②连续两帧相减导致两帧中目标重叠的部分被减掉, 从而检测不出来此部分, 造成空洞。而连续三帧差分法, 先将连续三帧中前后两帧分别差分, 从重合的部分中提取目标轮廓。比连续两帧差分法有明显改进, 其算法步骤如下:

步骤1 读取连续三帧图像 $\begin{matrix} f_{k - 1} 、 f_{k} 、 f_{k + 1}, 求出相邻两帧的差分图像 P_{k} 、 P_{k + 1}, 根据自适应阈值 T_{3}, 提取出运动区域并二值化, 得到 R_{k} 和 R_{k + 1} 。 \end{matrix}$

步骤2 将得到的 $\begin{matrix} R_{k} 和 R_{k + 1} \end{matrix}$ 按式(13)进行计算, 求得包含运动目标的二值图像:

$\begin{matrix} R_{k} (x, y) = \{\begin{matrix} 1, R_{k} (x, y) ⋂ R_{k + 1} (x, y) = 1 \\ 0, 其他 \end{matrix} (13) \end{matrix}$

在此方法中, 帧间差分阈值T₃的选取很关键, 传统的方法是根据不同的视频、不同的背景、不同的运动目标选取不同的阈值。因为每个视频都要选取阈值, 当背景发生变化或者目标发生变化时, 固定的阈值可能就不再适用, 带来的结果就是检测的准确率下降。本文采用自适应阈值的方法来解决此问题, 该方法可按一定的方式自动选取阈值, 并根据场景的变化不断变化。阈值的提取公式如下:

$\begin{matrix} \begin{matrix} T_{4} & = (median [P_{k} (x, y)] + \max [P_{k} (x, y)] + \\ \min [P_{k} (x, y)]) / 4 (14) \\ T_{3} & = T_{4} + 1.4826 \times median [P_{k 2} (x, y) - \\ median [P_{k 2} (x, y)]] (15) \end{matrix} \end{matrix}$

3 运动目标提取

在得到背景差分后的二值图像Z_k(x,y)和帧间差分后的二值图像R_k(x,y)后,可按下式进行运动目标的提取:

$\begin{matrix} F_{k} (x, y) = \{\begin{matrix} 1, Z_{k} (x, y) ⋃ R_{k} (x, y) = 1 \\ 0, 其他 \end{matrix} (16) \end{matrix}$

由于此方法结合了背景差分法和帧间差分法, 因此具有上述两种方法的优点, 形成互补。

对 $\begin{matrix} F_{k} \end{matrix}$ 进行3× 3形态学处理, 除去孤立噪声点, 结果记为 $\begin{matrix} F_{s} 。 \end{matrix}$ 在帧间差分的过程中, 可能存在将部分属于前景的像素点差分掉, 导致前景目标出现空洞。为尽可能使前景目标完整, 可采用基于形态学目标重构^[15]的方法:

$\begin{matrix} F = F_{s} ⋂ (F_{k} \oplus SE) (17) \end{matrix}$

式中: $\begin{matrix} F \end{matrix}$ 为目标重构后最终的分割结果; SE为结构元素, 其尺寸依赖于目标的大小, 实验表明, 7× 7的尺寸可以达到较好的效果。

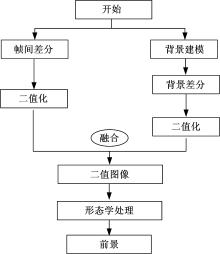
本文基于帧间差分法和背景差分法的运动目标检测算法流程如图1所示。

	Figure Option View Download New Window
	图1 本文检测算法Fig.1 Flow chart of proposed algorithm

4 仿真实验

为验证本文算法的检测结果, 在Matlab上进行了仿真实验。高斯混合模型的参数 $\begin{matrix} K \end{matrix}$ 为3; 初始方差为30; $\begin{matrix} α \end{matrix}$ 为0.02。

实验1为室外某男子的检测结果对比, 如图2所示。可以看出, 帧间差分法由于连续两帧相减, 造成检测结果里缺少很大部分真实目标。由于本视频拍摄的光线变化较少, 背景比较固定, 背景差分法的检测效果较好, 但是仍有少量空洞存在。本文算法结合了背景差分法和帧间差分法的优点, 再加入形态学滤波, 能有效抑制空洞, 检测效果较好。

	Figure Option View Download New Window
	图2 实验1检测结果的比较Fig.2 Result comparison by experiment 1

实验2为室外高速公路上的车辆检测结果对比, 如图3所示。可以看出, 帧间差分由于连续两帧相减, 造成检测结果里缺少部分真实目标。由于本视频拍摄环境较复杂, 背景模型变化较大, 导致传统背景差分法的检测效果不佳, 有大量噪声存在。本文算法将帧间差分与背景差分结合, 并对背景模型的更新做出修改, 使得背景模型更接近真实状态, 对于光线变化处理得很好, 有效避免了由于光线突变导致的检测误差。

	Figure Option View Download New Window
	图3 实验2检测结果的比较Fig.3 Result comparison by experiment 2

实验3为室外某男子的检测结果对比, 如图4所示。可以看出, 帧间差分法的检测结果里出了空洞, 也出现了部分噪声。而背景差分的检测结果中, 由于目标部分灰度与背景较接近, 导致部分目标被当做前景。本文算法在对差分阈值的选取上是自适应的, 在不同的情况下, 阈值可根据差分图像自适应调整, 因此检测结果更加准确。

	Figure Option View Download New Window
	图4 实验3检测结果的比较Fig.4 Result comparison by experiment 3

5 结束语

本文首先对运动目标检测的两种常见算法— — 帧间差分法和背景差分法进行探讨, 针对各自的缺点, 提出了一种新的算法, 将帧间差分与背景差分结合起来, 对背景模型中方差的更新作了改进, 用连续三帧差分代替两帧差分, 并使用自适应的阈值。实验表明, 本文算法能有效抑制噪声和空洞, 适应性强, 检测效果良好。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	汪冲, 席志红, 肖春丽. 基于背景差分的运动目标检测方法[J]. 应用科技, 2009, 36(10): 16-18. Wang Chong, Xi Zhi-hong, Xiao Chun-li. Moving objects detection based on background subtraction method[J]. Applied Science and Technology, 2009, 36(10): 16-18. [本文引用:1]
[2]	Piccardi M. Background subtraction techniques: a review[C]∥IEEE International Conference on Systems, Man and Cybemeties, Sydney, Australia, 2004: 3099-3104. [本文引用:1]
[3]	王振亚, 曾黄麟. 一种基于帧间差分和光流技术结合的运动车辆检测和跟踪新算法[J]. 计算机应用与软件, 2012, 29(5): 117-120. Wang Zhen-ya, Zeng Huang-lin. A new algorithm of moving vehicle detection and tracking based on combining frame difference method with optical flow technique[J]. Computer Applications and Software, 2012, 29(5): 117-120. [本文引用:1]
[4]	Tsai D M, Lai S C. Independent component analysis-based background subtraction for indoor surveillance[J]. IEEE Transactions on Image Processing, 2009, 18(1): 158-160. [本文引用:1]
[5]	Zhang Jie-yu, Barron J L. Optical flow at occlusion[C]∥The Ninth Conference on Computer and Robot Vision, Toronto, Canada, 2012: 198-205. [本文引用:1]
[6]	胡觉晖, 李一民, 潘晓露. 改进的光流法用于车辆识别与跟踪[J]. 科学技术与工程, 2010, 10(23): 5814-5817. Hu Jue-hui, Li Yi-min, Pan Xiao-lu. An improved optical flow algorithmin in vehicle identification and tracking[J]. Science Technology and Engineering, 2010, 10(23): 5814-5817. [本文引用:1]
[7]	Stauffer C, Grimson W E L. Adaptive background mixture models for real-time tracking[C]∥IEEE Computer Vision and Pattern Recognition, Fort Collins, USA, 1999: 246-250. [本文引用:1]
[8]	Zhang J, Chen C H. Moving objects detection and segmentation in dynamic video backgrounds[C]∥IEEE Conference on Technologies for Homeland Security, Woburn, MA, 2007: 64-69. [本文引用:1]
[9]	袁国武, 陈志强, 龚健, 等. 一种结合光流法与三帧差分法的运动目标检测算法[J]. 小型微型计算机系统, 2013, 34(3): 669-671. Yuan Guo-wu, Chen Zhi-qiang, Gong Jian, et al. A moving object detection algorithm based on a combination of optical flow and three-frame difference[J]. Journal of Chinese Computer Systems, 2013, 34(3): 6 69-671. [本文引用:1]
[10]	陈俊超, 张俊豪, 刘诗佳, 等. 基于背景建模与帧间差分的目标检测改进算法[J]. 计算机工程, 2011, 37(增刊): 171-173. Chen Jun-chao, Zhang Jun-hao, Liu Shi-jia, et al. Improved target detection algorithm based on background modeling and frame difference[J]. Computer Engineering, 2011, 37(Sup. ): 171-173. [本文引用:1]
[11]	王小平, 张丽杰, 常佶. 基于单高斯背景模型运动目标检测方法的改进[J]. 计算机工程与应用, 2009, 45(21): 118-120. Wang Xiao-ping, Zhang Li-jie, Chang Ji. Improved method of moving objects detection based on single-gaussian background mode[J]. Computer Engineering and Applications, 2009, 45(21): 118-120. [本文引用:1]
[12]	魏晓慧, 李良福, 钱钧. 基于混合高斯模型的运动目标检测方法研究[J]. 应用光学, 2010, 31(4): 574-578. Wei Xiao-hui, Li Liang-fu, Qian Jun. Moving object detection based on mixture Gaussian mode[J]. Journal of Applied Optics, 2010, 31(4): 574-578. [本文引用:1]
[13]	张俊根, 姬红兵. 高斯混合粒子PHD滤波被动测角多目标跟踪[J]. 控制与决策, 2011, 26(3): 413-417. Zhang Jun-gen, Ji Hong-bing. Gaussian mixture particle probability hypothesis density based passive bearings-only multi-target tracking[J]. Control and Decision, 2011, 26(3): 413-417. [本文引用:1]
[14]	Li Li, Xu Ji-ning. Moving human detection algorithm based on Gaussian mixture model[C]∥Proceedings of the 29th Chinese Control Conference, Beijing, 2010: 2853-2856. [本文引用:1]
[15]	Xu L Q, Land abaso J L, Lei B. Segmentation and tracking of multiple moving objects for intelligent video analysis[J]. BT Technology Journal, 2004, 22(3): 140-149. [本文引用:1]

2009

0.0

. 2009, 36(10):16-18 DOI:doi:10.3969/j.issn.1009-671X.2009.10.005

Moving objects detection based on background subtraction method

基于背景差分的运动目标检测方法

Wang Chong , Xi Zhi-hong , Xiao Chun-li.

汪冲, 席志红, 肖春丽

针对静止摄像机下的运动目标检测问题,提出了一种基于背景减法的运动目标检测算法.通过对一组连续视频进行处理,从中得到不含运动目标的背景图像.再利用背景差分的方法提取出运动目标.在确定比较阈值的过程中,一改以往通过实验不断调整的做法,提出了动态阈值的概念,从而增强了检测效果,提高了算法的可实施性.融入了高斯模型关于背景更新的算法,克服了由于背景突然改变而造成的误检测.实验结果表明,通过背景差分与高斯模型相结合的方法,在有诸多不确定性因素的序列视频中构建背景有较好的自适应性,能迅速响应实际场景的变化,为准确地检测出运动目标提供了必要的基础.

... 0 引言运动目标检测算法包括背景差分法^[1,2]、帧间差分法^[3,4]和光流法^[5,6]等 ...

2004

0.0

... 0 引言运动目标检测算法包括背景差分法^[1,2]、帧间差分法^[3,4]和光流法^[5,6]等 ...

2012

0.0

. 2012, 29(5):117-120 DOI:doi:10.3969/j.issn.1000-386X.2012.05.031

A new algorithm of moving vehicle detection and tracking based on combining frame difference method with optical flow technique

一种基于帧间差分和光流技术结合的运动车辆检测和跟踪新算法

Wang Zhen-ya , Zeng Huang-lin.

王振亚, 曾黄麟

摘　要：为了改进智能交通中的运动车辆检测和跟踪方法,提出一种基于改进的帧间差分和光流技术结合的运动车辆检测和跟踪的新方法。先用帧间差分法检测出运动物体的运动区域,再计算差值图中不为零处的光流,然后利用其光流场来实现运动目标的跟踪。为了减少计算量,提出一种基于最优估计的点匹配技术和光流均匀采样策略的光流场计算方法,并通过对灰度化后的光流场进行自适应阈值分割、形态学滤波等处理,实现了实时的运动目标检测和跟踪。

... 0 引言运动目标检测算法包括背景差分法^[1,2]、帧间差分法^[3,4]和光流法^[5,6]等 ...

2009

0.0

... 0 引言运动目标检测算法包括背景差分法^[1,2]、帧间差分法^[3,4]和光流法^[5,6]等 ...

2012

0.0

... 0 引言运动目标检测算法包括背景差分法^[1,2]、帧间差分法^[3,4]和光流法^[5,6]等 ...

2010

0.0

. 2010, 10(23):5814-5817 DOI:doi:10.3969/j.issn.1671-1815.2010.23.052

An improved optical flow algorithmin in vehicle identification and tracking

改进的光流法用于车辆识别与跟踪

Hu Jue-hui , Li Yi-min , Pan Xiao-lu.

胡觉晖, 李一民, 潘晓露

摘　要：利用帧间差分获取运动区域,采用梯度阈值获取二值图像,再提取运动区域目标特征点的光流,对光流矢量采取分段标注,设置感兴趣区域。利用光流特性实现目标的识别,定位与跟踪,对于运动目标的跟踪具有实时性和鲁棒性,能够用于车流量统计,对车辆辅助行驶研究起到一定的铺垫作用,实验结果证明该算法的有效性和实用性。

... 0 引言运动目标检测算法包括背景差分法^[1,2]、帧间差分法^[3,4]和光流法^[5,6]等 ...

1999

0.0

2007

0.0

2013

0.0

. 2013, 34(3):669-671 DOI:doi:10.3969/j.issn.1000-1220.2013.03.047

A moving object detection algorithm based on a combination of optical flow and three-frame difference

一种结合光流法与三帧差分法的运动目标检测算法

Yuan Guo-wu , Chen Zhi-qiang , Gong Jian

袁国武, 陈志强, 龚健

Moving objects detection is an important research of computer vision. Optical flow method is an important way, but it is limited to use because of its complexity. A moving object detection algorithm based on a combination of optical flow and the three-frame difference is proposed. The calculation of optical flow is simplified. Harris corners are detected, then the pixels are selected to compute optical flow information, which reduce the algorithm′s complexity. Because the detected moving target area is not complete, three-frame difference method is introduced as a supplement. The experimental results show that the algorithm can achieve real-time and have better results than anyone in these two separate algorithms.

运动目标的检测是计算机视觉研究的重要内容之一，光流法是其中的一种重要方法.由于计算光流的算法复杂，限制了它的使用.本文提出一种结合光流法与三帧差分法的运动目标检测算法，该算法简化了光流的计算，选择图像中具有代表性的Harris角点，只对这些像素点计算光流信息，有效地减少了复杂度，由于检测得到的运动目标区域不够完整，引入了三帧差分法作为简化光流法的补充.经过实验，该方法使光流法达到了实时性要求，取得了好的效果，优于单独运用两种方法中的任何一种取得的效果.

2011

0.0

. 2011, 37(增刊):171-173

Improved target detection algorithm based on background modeling and frame difference

基于背景建模与帧间差分的目标检测改进算法

Chen Jun-chao , Zhang Jun-hao , Liu Shi-jia

陈俊超, 张俊豪, 刘诗佳

摘　要：在分析现有运动目标检测算法的基础上,提出一种基于背景建模与帧间差分的运动目标检测改进算法。改进算法能改善混合高斯背景相减法中高斯背景建模产生的鬼影,以及帧间差分法的前景检测结果中出现的严重拖影和空洞现象,并且在背景突变下也能进行有效检测。测试结果表明,改进算法对运动目标检测有较好的检测效果,适用于户外大型场所的监控设备领域。

2009

0.0

. 2009, 45(21):118-120 DOI:doi:10.3778/j.issn.1002-8331.2009.21.035

Improved method of moving objects detection based on single-gaussian background mode

基于单高斯背景模型运动目标检测方法的改进

Wang Xiao-ping , Zhang Li-jie , Chang Ji.

王小平, 张丽杰, 常佶

In order to overcome the deficiency of updating the background model and removing the shadow when the background subtraction method is applied to detect moving objects，an improved algorithm based on the single-Gaussian background model is proposed.The experimental results indicate that the algorithm can remove the shadow and extract the moving object effectively，which lays a solid foundation for the following work such as body recognization，behavior analysis and so on.

针对背景减除法应用于运动目标检测中的背景模型更新和阴影消除问题，提出了一种改进的单高斯背景模型估计算法和快速的阴影消除方法。实验结果表明，算法在有效去除阴影的同时能够较好地提取运动目标，为后续的人体识别、行为分析等工作奠定了良好的基础。

... 但是在环境变化较复杂的室外,单高斯分布^[11]的模型会出现较大偏差,容易将晃动的树叶、喷泉等背景误认为前景 ...

2010

0.0

. 2010, 31(4):574-578 DOI:doi:10.3969/j.issn.1002-2082.2010.04.014

Moving object detection based on mixture Gaussian mode

基于混合高斯模型的运动目标检测方法研究

Wei Xiao-hui , Li Liang-fu , Qian Jun.

魏晓慧, 李良福, 钱钧

In order to detect moving object in image scene in time, this paper presents a moving object detection method based on mixture Gaussian model. We regard the image pixel value as the synthesized process of the foreground Gauss distribution and the background Gauss distribution, and realize the background estimation and adaptive background update. Through performing multiple object segmentation after background subtraction, we can successfully detect multiple moving objects. The experiments show that when the background of image sequence is changing, the mixture Gaussian model based algorithm can estimate changed background accurately, and through subtraction between scene image and background image, the interested moving object can be detected. The experimental results for real image sequences demonstrate this moving object detection algorithm based on mixture Gaussian model is efficient.

为了能够及时检测到图像场景中的运动目标，提出一种基于混合高斯模型的运动目标检测方法。借助把图像的像素值看成是前景高斯分布和背景高斯分布的组合，进行了背景估计和自适应背景更新；通过对背景差分后的图像进行多目标分割，进行了多个运动目标的检测。实验发现：随着图像序列的背景不断变化，基于混合高斯模型算法能够准确估计出变化的背景，通过将场景图像和背景图像进行差分，检测到感兴趣的运动目标。

... 因此,本文采用混合高斯模型算法^[12]来进行背景建模,能较好地处理背景混乱和光线突然变化等干扰 ...

2011

0.0

. 2011, 26(3):413-417 DOI:doi:10.1097/IGC.0b013e31820fa168

Gaussian mixture particle probability hypothesis density based passive bearings-only multi-target tracking

高斯混合粒子PHD滤波被动测角多目标跟踪

Zhang Jun-gen , Ji Hong-bing.

张俊根, 姬红兵

为解决目标数未知或随时间变化的多日标跟踪问题,通常将多目标状态和脱测数据表示成随机集形式,并通过递推计算目标状态联合分布的概率假设密度(PHD)来完成,然而,对于被动测角的非线性跟踪问题,PHD无法获得闭合解,为此挺出一种新的高斯混合粒了PHD算法,该算法利用高斯混合近似PHD,以避免用聚类确定目标状态,并采用拟蒙特卡罗(QMC)积分方法计算日标状态的预测和更新分布,仿真结果验证了所提出算法的有效性.

... 对这些像素值使用k个高斯分布来进行描述,则xt的概率密度函数由k个高斯分布的加权混合表示如下^[13]: ...

2010

0.0

... 与 xt相匹配的的高斯分布的参数按如下公式^[14]进行更新: ...

2004

0.0

... 为尽可能使前景目标完整,可采用基于形态学目标重构^[15]的方法: ...