基于十字型阵列的并行子阵波束形成算法

引用本文

刘雪松, 周凡, 周泓, 田翔, 蒋荣欣, 陈耀武. 基于十字型阵列的并行子阵波束形成算法.吉林大学学报:工学版, 2016, 46(4): 1330-1336
LIU Xue-song, ZHOU Fan, ZHOU Hong, TIAN Xiang, JIANG Rong-xin, CHEN Yao-wu. Parallel subarray beamforming algorithm based on cross array. Journal of Jilin University Engineering and Technology Edition, 2016, 46(4): 1330-1336 复制到剪切板

Permissions

基于十字型阵列的并行子阵波束形成算法

刘雪松^1,², 周凡^1,^2,³, 周泓^1,², 田翔^1,^2,³, 蒋荣欣^1,^2,³, 陈耀武^1,^2,³

1.浙江大学数字技术及仪器研究所,杭州 310027

2.浙江省网络多媒体技术研究重点实验室,杭州 310027

3.浙江大学工业控制技术国家重点实验室,杭州 310027

通讯作者：周凡(1978-),男,副教授,博士.研究方向:嵌入式系统,声纳信号处理,多媒体技术,FPGA并行计算.E-mail:fanzhou@mail.bme.zju.edu.cn

作者简介:刘雪松(1988-),男,博士研究生.研究方向:嵌入式系统,声纳信号处理.E-mail:11015006@zju.edu.cn

基金:国家自然科学基金项目(41276090); “863”国家高技术研究发展计划项目(2014AA091301); 中央高校基本科研业务费专项资金项目

摘要

针对基于平面阵三维声纳成像系统应用中硬件开销及波束形成计算量大的问题,提出了一种基于十字型阵列的并行子阵波束形成算法。十字型阵列采用两条一维线阵实现了三维声纳成像,相比于二维平面阵,极大地简化了硬件复杂度。并行子阵算法在此基础上对十字型阵列的接收波束形成过程进行优化。算法将接收阵划分为多个子阵,在各子阵上并行地进行一级频域波束形成,在各子阵之间执行二级波束域波束形成,该两级并行流水线结构,有效地降低了波束形成的计算量。此外,给出了算法在现场可编程门阵列(FPGA)平台上的实现架构。仿真结果显示:本文算法获得了与直接波束形成相近的波束性能,但计算量仅为其一半,并且随着波束数量的增加,其优势会更加明显。

关键词: 信息处理技术; 并行子阵波束形成; 子阵划分; 十字型阵列; 计算量需求

中图分类号:TN911.7 文献标志码:A 文章编号:1671-5497(2016)04-1330-07

Parallel subarray beamforming algorithm based on cross array

LIU Xue-song^1,², ZHOU Fan^1,^2,³, ZHOU Hong^1,², TIAN Xiang^1,^2,³, JIANG Rong-xin^1,^2,³, CHEN Yao-wu^1,^2,³

1.Institute of Advanced Digital Technology and Instrumentation, Zhejiang University,Hangzhou 310027,China

2.Zhejiang Provincial Key Laboratory for Network Multimedia Technologies,Hangzhou 310027,China

3.State Key Laboratory of Industrial Control Technology,Zhejiang University,Hangzhou 310027,China

Abstract

To overcome the problem of huge hardware cost and computational load associated with the planar array in 3D sonar imaging application, a parallel subarray beamforming algorithm based on the cross array is proposed. The cross array can achieve 3D sonar image by two 1D linear arrays, which greatly simplifies the hardware complexity compared to planar array. The proposed algorithm is applied to optimize the receiving beamforming procedure of the cross array, and subdivide the receiving array into several subarrays. The first-stage frequency-domain beamforming is performed simultaneously in each subarray, and the second-stage beam-domain beamforming is implemented between the subarrays. The two-stage parallel and pipeline framework efficiently reduces the computational requirement of the beamforming. Moreover, the architecture of the algorithm on Field Programmable Gate Array (FPGA) is given. The simulation and analysis results demonstrate that the proposed algorithm can achieve similar beam performance but save half of the computational requirement compared to the direct method. As the number of beams increases, the superiority of the proposed algorithm becomes more obvious.

Keyword: information processing; parallel subarray beamforming; subarray decomposition; cross array; computational requirement

Show Figures

0 引言

三维声纳成像系统^[1]在水下探测、海底地貌测绘、海洋地质考察、海底施工、水下机器人、沉积物打捞等众多水下应用领域的作用日渐明显, 具有广阔的发展前景^{[2, 3]}。

波束形成是三维声纳成像系统中最常采用的方法之一。声纳信号的波束形成是对某些特定方向上信号进行加强, 对其他方向上信号进行削弱的一种空间滤波算法^[4]。通常, 为获得三维声纳图像, 需要一个二维接收换能器阵列, 接收观测场景的回波信号, 并对其进行波束形成计算^[5]。而二维平面阵列存在两个问题制约着三维声纳成像系统的发展:①大量的换能器数量, 导致前端信号通道硬件开销巨大; ②数字波束形成算法所需的计算量庞大, 难以工程实现^[6]。针对上述两个问题, Repetto等^[6]利用模拟退火(Simulating annealing)算法对平面换能器阵列进行稀疏化处理, 使得非等间距稀疏阵列在保持系统性能不变的前提下, 减小了硬件开销。陈朋等^[7]利用声纳回波信号的位移矢量分解及合成原理, 对三维声纳频域波束形成算法进行了优化, 减少了算法所需的内存空间。Palmese等^[8]提出了一种CZT波束形成算法, 成功地减少了1~2个数量级的计算量。此外, 一些学者将发射波束形成和接受波束形成相结合, 基于十字型阵列(Cross array), 实现三维图像的构建。MacPhie^[9]证明了十字型阵列能够以M+N的阵元数量, 获得与平面阵(阵元数量M× N)相同的性能。文献[10, 11]设计实现了基于十字型阵列的海底地形测绘系统, 并进行了实际的海底测试, 得到了海底地形的三维声学图像。

本文基于十字型阵列, 提出了一种工作在远场的并行子阵波束形成(Parallel subarray beamforming, PSB)算法, 优化了十字型阵列的接收波束形成过程。该算法将接收阵列分解为多个子阵:首先, 在每个子阵中并行地进行一级波束形成; 然后, 抽取一级波束结果, 在子阵之间进行二级波束形成, 得到的结果即为最终的波束强度。并行子阵算法的两级并行流水线结构, 在降低了波束形成算法计算量的同时, 也保持了与十字型阵列直接波束形成(Direct method, DM)算法相近的波束性能。结合十字型阵列本身降低了系统的硬件复杂度, 该算法很大程度上解决了制约三维声纳成像发展的两个问题。此外, 本文还给出了并行子阵波束形成算法的现场可编程门阵列(FPGA)平台实现。通过仿真实验和分析, 证明了该算法的有效性和优越性。

1 十字型阵列波束形成

十字型阵列由两条相互垂直的线阵组成:一条作为发射阵列; 一条作为接收阵列。利用发射和接收阵列分别在垂直和水平方向上的波束指向性, 实现三维图像的构建。

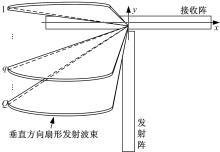
首先, 垂直发射线阵(包含N路阵元)通过对各路阵元发射信号进行相移, 各路发射信号经过叠加, 向预设垂直波束方向(Steering direction)发射扇形波束, 如图1所示。发射波束形成的相移参数θ _n(远场)和波束方向图BP_Tr可表示为^[4]:

	Figure Option View Download New Window
	图1 十字阵发射波束形成示意图Fig.1 Transmitting beamforming of cross array

$\begin{matrix} \begin{matrix} θ_{n} & = 2 π f_{0} \cdot (n - 1) d_{t} \cdot \sin β_{q} / c (1) \\ B P_{Tr} & = |\overset{N}{\sum_{n = 1}} S_{n} (k) \cdot \exp (- j θ_{n})| (2) \end{matrix} \end{matrix}$

式中:f₀为发射信号的中心频率; n(1≤ n≤ N)为发射阵元的序号, 发射波束形成以第一个发射阵元为参考点; d_t为发射阵元间距; β _q为垂直方向的波束方向角, q(1≤ q≤ Q)为其索引号; S_n(k)为发射信号的L点离散傅里叶变换(Discrete fourier transform, DFT)结果, k为其线谱号; c为声纳信号在水下传播的速度(1500 m/s)。

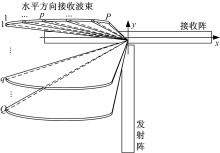
随后, 当发射阵列向一个波束方向发射结束后, 接收阵列接收来自该方向的回波信号, 并在该波束扇面内进行水平方向的频域波束形成, 如图2所示。接收波束形成完成后, 发射阵列向下一个垂直波束方向进行发射。接收波束形成的相移参数θ _m(远场)和波束方向图BP_Re可表示为:

$\begin{matrix} \begin{matrix} θ_{m} = 2 π f_{0} \cdot (m - \frac{M + 1}{2}) d_{r} \cdot \sin α_{p} / c (3) \\ B P_{Re} = |\overset{M}{\sum_{m = 1}} S_{m} (k) \cdot \exp (- j θ_{m})| (4) \end{matrix} \end{matrix}$

式中:m(1≤ m≤ M)为接收阵元的序号, 接收波束形成以接收阵中点为参考点; d_r为接收阵元间距; α _p为水平方向的波束方向角; p(1≤ p≤ P)为其索引号; S_m(k)为接收回波信号的L点DFT结果。

	Figure Option View Download New Window
	图2 十字阵接收波束形成示意图Fig.2 Receiving beamforming of cross array

当完成所有垂直及水平方向的波束形成后, 则可得到整个场景的波束强度信息(共P× Q个波束), 构建三维声纳图像。十字型阵列整体波束方向图为接收和发射波束方向图的乘积^[1], 其表达式为:

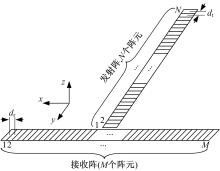
$\begin{matrix} BP = |B P_{Re}| \cdot |B P_{Tr}| (5) \end{matrix}$

2 并行子阵波束形成算法

十字型阵列配置如图3所示。其发射信号采样点通过预先计算, 存储在内存中, 不需要额外计算量。因此, 本文提出的PSB算法目的在于优化十字型阵列的接收波束形成过程, 降低其计算量, 有利于工程化实现。

	Figure Option View Download New Window
	图3 十字型阵列配置Fig.3 Configuration of cross array

PSB算法的核心思想是将接收阵列分成多个子阵, 利用远小于整阵的子阵规模, 以及算法的两级并行流水线结构, 提高波束形成的计算效率。子阵划分示意图如图4所示。

	Figure Option View Download New Window
	图4 子阵划分示意图Fig.4 Decomposition of subarray

2.1 一级波束形成

如图4所示, 接收阵被划分为M_S个子阵, 每个子阵包含M_F个阵元, 子阵阵元间距为d_r, 子阵间间距为M_F× d_r。当接收阵接收到声纳回波后, 各阵元通道对回波信号进行采样。为获得回波信号的频域信息, 对各通道的采样数据进行L点DFT运算, 抽取回波信号中心频率对应的频谱值, 子阵中DFT运算的变换公式如下:

$\begin{matrix} \begin{matrix} S_{m_{F}} (k) & = \overset{L}{\sum_{l = 1}} s_{m_{F}} (l) \cdot \exp (- j \frac{2 π}{L} l \cdot k) (6) \\ k & = L \cdot f_{0} / f_{s} (7) \end{matrix} \end{matrix}$

式中:k表示中心频率f₀对应的线谱号; $\begin{matrix} S_{m_{F}} \end{matrix}$ (k)为其DFT结果; $\begin{matrix} s_{m_{F}} \end{matrix}$ (l)是回波信号的采样数据, 其中m_F(1≤ m_F≤ M_F)代表子阵中阵元的序号; f_s为采样频率。

若一级波束形成在每个子阵中生成P_F个波束(通常P_F≤ P), 则其相移参数 $\begin{matrix} θ_{m_{F}} \end{matrix}$ 和波束方向图BP₁可表示如下:

$\begin{matrix} θ_{m_{F}} \end{matrix}$ =2π f₀· $\begin{matrix} (m_{F} - \frac{M_{F} + 1}{2}) \end{matrix}$ d_r· sin $\begin{matrix} α_{p_{F}} \end{matrix}$ /c (8)

$\begin{matrix} B P_{1} = |\overset{M_{F}}{\sum_{m_{F} = 1}} S_{m_{F}} (k) \cdot \exp (- j θ_{m_{F}})| (9) \end{matrix}$

式中: $\begin{matrix} α_{p_{F}} \end{matrix}$ 为子阵一级波束形成的水平波束方向角, p_F(1≤ p_F≤ P_F)为其索引号。

2.2 二级波束形成

一级波束形成完成后, 以各子阵为基本阵元, 在子阵之间进行二级波束形成, 阵元间距为M_F× d_r, 最终生成P个波束。二级波束形成以一级波束结果作为采样数据, 从频域转换为波束域进行计算。因此, 首先要对各子阵一级波束结果进行抽取, 在抽取过程中保证二级波束方向角α _p尽可能接近一级波束方向角 $\begin{matrix} α_{p_{F}} \end{matrix}$ , 即:

$\begin{matrix} α_{p} \approx α_{p_{F}} (10) \end{matrix}$

由式(10)可得, 二级波束索引号p和一级索引号p_F的关系如下:

$\begin{matrix} \frac{(p - 1) α_{\max}}{(P - 1)} \approx \frac{(p_{F} - 1) α_{\max}}{(P_{F} - 1)} (11) \end{matrix}$

式中:α _max为角度覆盖范围, 则有:

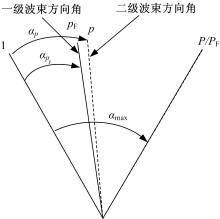
$\begin{matrix} \begin{matrix} p_{F} = round [\frac{(p - 1) (P_{F} - 1)}{(P - 1)} + 1] \\ (12) \end{matrix} \end{matrix}$

式中:round[* ]表示对结果进行四舍五入。波束抽取示意图如图5所示。

	Figure Option View Download New Window
	图5 波束抽取示意图Fig.5 Extraction of beam results

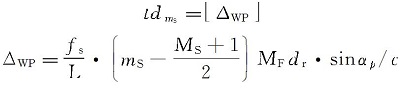
一级波束结果作为二级波束形成的采样数据, 其采样频率降为f_s/L。由于各子阵间回波存在波程差, 因此场景中同一个目标的回波, 对于不同的子阵, 其对应的一级波束结果可能在不同的采样时刻完成, 即其一级波束结果的输出顺序不同。故在二级波束形成中, 需要引入一个时延参数, 配合相移参数进行补偿。则一级波束结果可重新表示为BP₁(t $\begin{matrix} d_{m_{S}} \end{matrix}$ ), 其中时延参数t $\begin{matrix} d_{m_{S}} \end{matrix}$ 代表一级波束结果的相对采样时刻顺序(即结果输出顺序), m_S(1≤ m_S≤ M_S)为子阵序号, 其表达式为:

式中: · 表示对结果进行向下取整; Δ _WP为波程差, 以接收阵中点为参考点。

由式(13)可知, 时延参数为波程差结果向下取整的整数部分, 代表子阵之间一级波束结果计算输出顺序的相对差值。波程差结果的小数部分转换为相移参数, 对其进行相位补偿。在计算相移参数 $\begin{matrix} θ_{m_{S}} \end{matrix}$ 时, 其对应的信号频率仍为f₀, 其表达式为:

$\begin{matrix} θ_{m_{S}} = 2 π f_{0} \frac{L}{f_{s}} \cdot (Δ_{WP} - t d_{m_{S}}) (15) \end{matrix}$

则二级波束形成的波束方向图BP₂可表示如下:

$\begin{matrix} B P_{2} = |\overset{M_{S}}{\sum_{m_{S} = 1}} B P_{1} (t d_{m_{S}}) \cdot \exp (- j θ_{m_{S}})| (16) \end{matrix}$

根据式(12), 抽取一级波束结果进行二级波束形成计算, 得到的结果即为最终波束强度结果。

3 PSB算法的FPGA实现

3.1 FPGA实现

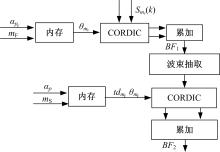
由式(9)及式(16)可知, PSB算法的两级波束形成的累加项均为复数的相位旋转, 采用CORDIC(Coordinate rotation digital computer)算法^[12]可直接实现相位旋转功能, 然后对结果进行累加, 最终即可得到波束强度结果。PSB算法的数据通路如图6所示。

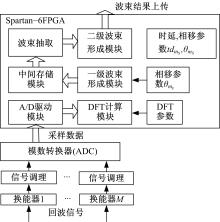
	Figure Option View Download New Window
	图6 PSB算法数据通路Fig.6 Data path of PSB algorithm

基于PSB算法的数据通路, 选用Spartan-6系列FPGA作为核心平台, 设计实现了PSB算法基于FPGA平台的系统架构。声纳回波信号通过接收换能器转换为电信号, 经过信号调理及A/D转换电路, 变换为数字信号传输至FPGA, 进行波束形成计算, 最终将波束结果上传至上位机显示, 其结构框图如图7所示。

	Figure Option View Download New Window
	图7 FPGA结构框图Fig.7 Architecture of FPGA

3.2 计算量分析

为评估PSB算法的计算量需求, 基于上述数据通路及FPGA结构, 对算法的计算量进行分析, 并与十字型阵列的DM接收波束形成算法进行对比。

对于PSB和DM算法, 其均为频域波束形成算法, 因此首先需要对各通道采样数据进行DFT运算, 采样点数为L。接收阵元数量为M, 每个通道完成一次DFT运算需要2L次实数乘法以及2(L-1)次实数加法, 则DFT所需实数计算量CL_DFT为:

$\begin{matrix} \begin{matrix} C L_{DFT} = [2 L + 2 (L - 1)] \cdot M = \\ (4 L - 2) \cdot M (17) \end{matrix} \end{matrix}$

对于DM算法, 计算一个波束, 由式(4)可知, 需要M次复数乘法(一次复乘包含4次实数乘法和2次实数加法)以及M-1次复数加法(一次复加包含2次实数加法), 若波束数为P, 则DM算法的波束形成的计算量CL_BF为:

$\begin{matrix} \begin{matrix} C L_{BF} = (4 M + 2 M + 2 M - 2) \cdot P = \\ (8 M - 2) \cdot P (18) \end{matrix} \end{matrix}$

由此可知, DM算法的总计算量CL_DM为:

$\begin{matrix} \begin{matrix} C L_{DM} = C L_{DFT} + C L_{BF} = (4 L - 2) \cdot \\ M + (8 M - 2) \cdot P (19) \end{matrix} \end{matrix}$

对于PSB算法, 根据式(9)和式(16), 采用CORDIC算法, 一级波束形成生成P_F个波束需要M_F× P_F次相位旋转(即M_F× P_F次实数运算), 以及(M_F-1)× P_F次复数加法(CORDIC结果累加); 二级波束形成生成P个波束需要M_S× P次实数运算, 以及(M_S-1)× P次复数加法。则两级波束形成计算量CL_F和CL_S分别为:

$\begin{matrix} \begin{matrix} C L_{F} = M_{F} P_{F} + 2 (M_{F} - 1) P_{F} = (3 M_{F} - 2) P_{F} (20) \\ C L_{S} = M_{S} P + 2 (M_{S} - 1) P = (3 M_{S} - 2) P (21) \end{matrix} \end{matrix}$

故PSB算法的总计算量CL_PSB为:

$\begin{matrix} \begin{matrix} C L_{PSB} = C L_{DFT} + M_{S} \cdot C L_{F} + C L_{S} = (4 L - \\ 2) M + (3 M_{F} - 2) P_{F} \cdot M_{S} + (3 M_{S} - 2) P (22) \end{matrix} \end{matrix}$

为了对两种波束形成算法的计算效率进行对比, 在相同阵列配置的条件下:接收阵阵元数量M=100; DFT点数L=150; 子阵阵元数量M_F=10; 子阵数量M_S=10; 一级波束数P_F=26, 根据式(19)及式(22), 分别计算当波束数P为50、100和150的情况下, DM算法和PSB算法的计算量, 其结果对比如表1所示。

表1 DM及PSB算法计算量对比 Table 1 Comparisons of computational load between DM and PSB

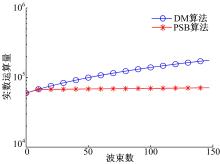
在上述实验环境下, DM及PSB算法计算量随波束数变化的趋势如图8所示。

	Figure Option View Download New Window
	图8 计算量随波束数变化示意图Fig.8 Computational load vs beam numbers

由图8和表1可以看出, PSB算法的计算量随波束数P增长变化不明显。对于PSB算法而言, 决定其计算量的主要因素是DFT的计算量CL_DFT, 其次是一级波束形成的计算量M_S× CL_F(主要取决于P_F), 二级波束形成的计算量CL_S对整体影响不大(M_S一般较小), 而DM算法计算量则随P增大而线性增加。因此, 波束数P越大, PSB算法在降低计算量方面的优势也越明显。当P=100时, PSB算法的计算量需求约为DM算法的二分之一。

4 仿真实验及分析

为验证PSB算法的有效性, 在Matlab仿真环境中, 对算法不同子阵划分情况下的归一化波束方向图进行仿真实验, 并与十字型阵列的DM接收波束形成算法进行对比。仿真环境设置如下:整阵阵元数量M=100; 总波束方向数P=100; 阵元间距d_r=1.5 mm; 信号中心频率f₀=500 kHz; 采样频率f_s=3 MHz; 场景角度覆盖α _max=± 50° ; DFT点数L=150。

假设在-15.66° (随意选取的一个预设波束方向)存在一个单点目标, 在以下4种子阵划分情况下进行仿真:①子阵阵元数M_F=10, 子阵数M_S=10, 一级波束数P_F=26; ②子阵阵元数M_F=25, 子阵数M_S=4, 一级波束数P_F=16; ③子阵阵元数M_F=25, 子阵数M_S=4, 一级波束数P_F=26; ④子阵阵元数M_F=10, 子阵数M_S=10, 一级波束数P_F=100。

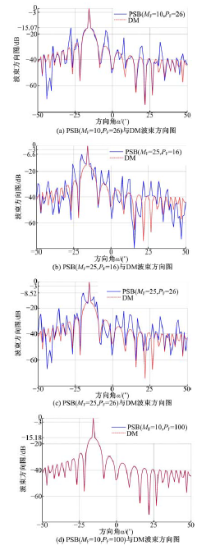
仿真结果如图9所示。

PSB算法中, 由于二级波束形成的近似波束抽取过程, 使得PSB算法与DM算法相比存在一定误差。作为一种近似波束形成算法, 其近似精度与子阵阵元数M_F及一级波束数P_F相关。结合仿真结果, 可得到如下结论:

(1)PSB算法不论在何种子阵划分条件下, 可以获得与DM算法完全相同的主瓣性能(主瓣宽度, -3 dB处测得, 均为0.4° ), 如图9所示。

	Figure Option View Download New Window
	图9 PSB算法与DM算法波束方向图对比Fig.9 Comparisons of beam pattern in PSB and DM

(2)由图9(a)、9(d)可知, PSB算法的近似主要由二级波束形成中的近似波束抽取造成, 当一级波束数等于总波束数时(即P_F=P), PSB算法可获得与DM算法相同的波束性能, 如图9(d)所示。

(3)由图9(b)、9(c)可知, 在子阵阵元数M_F相同的情况下, 当一级波束数不等于总波束数时(即P_F≠ P), 一级波束数P_F越大, PSB算法获得的旁瓣峰值越低(P_F=16时, 旁瓣峰值为-6.6 dB; P_F=26时, 旁瓣峰值为-8.52 dB)。

(4)由图9(a)、9(c)可知, 当一级波束数不等于总波束数时(即P_F≠ P), PSB算法会引入一些新的旁瓣。新引入的旁瓣主要由二级波束形成补偿参数的周期变化造成。由式(13)(14)(15)可知, PSB算法的二级波束形成阵元间距变为M_F× d_r, 而旁瓣则是波束方向图的周期性极值。因此, M_F越大, 补偿参数的周期越短, 旁瓣出现的位置距主瓣越近, 而此处一级波束结果的衰减不够大, 则会出现比较高的旁瓣峰值(M_F=10时, 旁瓣峰值为-15.07 dB; M_F=25时, 旁瓣峰值为-8.52 dB)。

(5)由4组实验结果对比可知, 子阵阵元数M_F越小, 一级波束数P_F越大, PSB算法的波束性能与DM算法越接近(当M_F=0, P_F=P时, PSB算法完全等同于DM算法), 但是根据式(22), 其相应的计算量也越大。

(6)在十字型阵列的波束形成中采用PSB算法进行子阵划分时, 需要综合考虑3个因素:波束方向图的主瓣宽度、旁瓣峰值以及波束形成的计算量。合理的子阵划分方式能够使主瓣宽度更窄、旁瓣峰值更低、计算量更小。在实际工程应用中, 为降低波束形成计算量, 可以选择牺牲较少的旁瓣性能, 以满足其实时性需求。在本实验中, 通过对多种子阵划分方式波束方向图的仿真, 得到较为合理的子阵划分方式为:子阵阵元数M_F=10, 一级波束数P_F=26。该子阵划分方式获得的主瓣宽度与DM算法一致, 旁瓣峰值为-15.07 dB, 相比DM算法仅增大0.11 dB, 并且计算量得到大幅降低, 通过设置阈值, 将小于-15 dB的波束信号滤除掉, 便可保证不会出现目标的误识别。

5 结束语

提出了一种基于十字型阵列的远场频域并行子阵波束形成算法, 优化了十字型阵列的接收波束形成过程。PSB算法在获得与十字型阵列直接波束形成算法相近的波束性能的同时, 降低了波束形成的计算量需求, 便于其工程化实现。此外, PSB算法也可扩展到平面阵, 在平面阵波束形成应用中, 其降低计算量的优势将会更加明显。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Murino V, Trucco A. Three-dimensional image generation and processing in underwater acoustic vision[J]. Proceedings of the IEEE, 2000, 88(12): 1903-1948. [本文引用:2]
[2]	Wachowski N, Azimi-Sadjadi M R. A new synthetic aperture sonar processing method using coherence analysis[J]. IEEE Journal of Oceanic Engineering, 2011, 36(4): 665-678. [本文引用:1]
[3]	Palmese M, Trucco A. Acoustic imaging of underwater embedded objects: signal simulation for three-dimensional sonar instrumentation[J]. IEEE Transactions on Instrumentation and Measurement, 2006, 55(4): 1339-1347. [本文引用:1]
[4]	Nielsen R O. Sonar Signal Processing[M]. Boston: Artech House, 1991: 51-52. [本文引用:2]
[5]	Trucco A. Thinning and weighting of large planar arrays by simulated annealing[J]. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 1999, 46(2): 347-355. [本文引用:1]
[6]	Repetto S, Palmese M, Trucco A. Design and assessment of a low-cost 3-D sonar imaging system based on a sparse array[C]∥IEEE Instrumentation and Measurement Technology Conference, Sorrento, 2006: 410-415. [本文引用:2]
[7]	陈朋, 陈耀武. 三维声纳频域波束形成算法的优化及实现[J]. 吉林大学学报: 工学版, 2010, 40(3): 830-835. Chen Peng, Chen Yao-wu. 3D sonar frequency-domain beamforming algorithm-optimization and implementation[J]. Journal of Jilin University (Engineering and Technology Edition), 2010, 40(3): 830-835. [本文引用:1]
[8]	Palmese M, Trucco A. Three-Dimensional acoustic imaging by chirp zeta transform digital beamforming[J]. IEEE Transactions on Instrumentation and Measurement, 2009, 58(7): 2080-2086. [本文引用:1]
[9]	MacPhie R H. A mills cross multiplicative array with the power pattern of a conventional planar array[C]∥Proc IEEE Antennas and Propagation Soc Int Symp, Honolulu, HI, 2007: 5961-5964. [本文引用:1]
[10]	Henderson T L, Lacker S G. Seafloor profiling by a wideband sonar: simulation, frquency-response optimization, and results of a brief sea test[J]. IEEE Journal of Oceanic Engineering, 1989, 14(1): 94-107. [本文引用:1]
[11]	Okino M, Higashi Y. Measurement of seabed topography by multibeam sonar using CFFT[J]. IEEE Journal of Oceanic Engineering, 1986, 11(4): 474-479. [本文引用:1]
[12]	Volder J E. The CORDIC trigonometric computing technique[J]. IRE Trans on Electronic Computers, 1959, 8(3): 330-334. [本文引用:1]

2000

0.0

... 0 引言三维声纳成像系统^[1]在水下探测、海底地貌测绘、海洋地质考察、海底施工、水下机器人、沉积物打捞等众多水下应用领域的作用日渐明显,具有广阔的发展前景^[2,3] ...

... 十字型阵列整体波束方向图为接收和发射波束方向图的乘积^[1],其表达式为: ...

2011

0.0

2006

0.0

1991

0.0

... 声纳信号的波束形成是对某些特定方向上信号进行加强,对其他方向上信号进行削弱的一种空间滤波算法^[4] ...

... _n(远场)和波束方向图BP_Tr可表示为^[4]: ...

1999

0.0

... 通常,为获得三维声纳图像,需要一个二维接收换能器阵列,接收观测场景的回波信号,并对其进行波束形成计算^[5] ...

2006

0.0

... ②数字波束形成算法所需的计算量庞大,难以工程实现^[6] ...

... 针对上述两个问题,Repetto等^[6]利用模拟退火(Simulating annealing)算法对平面换能器阵列进行稀疏化处理,使得非等间距稀疏阵列在保持系统性能不变的前提下,减小了硬件开销 ...

2010

0.0

. 2010, 40(3):830-835

3D sonar frequency-domain beamforming algorithm-optimization and implementation

三维声纳频域波束形成算法的优化及实现

Chen Peng , Chen Yao-wu.

陈朋, 陈耀武

A new optimization algorithm for threedimensional (3D) sonar beamforming in the frequencydomain is proposed. The relationship between the beam intensity and azimuth angle is derived based on the resolution of echo displacement vector, and then the algorithm is optimized. Simulation of the algorithm is conducted in Matlab and two datapaths for the proposed algorithm are demonstrated. The memory and the computational requirements for the proposed datapaths are also analyzed. Finally, under the Xilinx ISE environment, simulations for the two datapaths are carried out on FieldProgrammable Gate Arrays (FPGAs) respectively, and the resource utilizations are listed. It is demonstrated that the proposed algorithm possesses the advantage to reduce the memory requirements without sacrificing the system performance.

为了对三维声纳频域波束形成算法进行优化，提出了一种算法的优化方法。利用声纳回波信号的位移矢量分解与合成原理，推导出波束强度与相应方向角的数学关系式，进而使算法得到优化，并对优化的波束形成算法进行了仿真。同时，给出了实现此算法的两种数据通路，并对其内存需求量和计算量进行了分析。最终在Xilinx ISE环境下，在现场实现可编程门阵列（FPGA）上对该两种数据通路进行了仿真，并列出了相应的资源利用情况。优化后的算法不仅可以得到与传统算法相同的波束强度矩阵结果，而且减少了存储相移参数所需的内存空间。

... 陈朋等^[7]利用声纳回波信号的位移矢量分解及合成原理,对三维声纳频域波束形成算法进行了优化,减少了算法所需的内存空间 ...

2009

0.0

... Palmese等^[8]提出了一种CZT波束形成算法,成功地减少了1~2个数量级的计算量 ...

2007

0.0

... MacPhie^[9]证明了十字型阵列能够以M+N的阵元数量,获得与平面阵(阵元数量M#cod#x000D7 ...

1989

0.0

1986

0.0

1959

0.0

... 1 FPGA实现由式(9)及式(16)可知,PSB算法的两级波束形成的累加项均为复数的相位旋转,采用CORDIC(Coordinate rotation digital computer)算法^[12]可直接实现相位旋转功能,然后对结果进行累加,最终即可得到波束强度结果 ...