基于星载混合相控阵MIMO SAR的多方向测绘带成像及二维DBF处理

引用本文

张乐乐, 陈殿仁, 赵爽. 基于星载混合相控阵MIMO SAR的多方向测绘带成像及二维DBF处理.吉林大学学报:工学版, 2016, 46(4): 1344-1353
ZHANG Le-le, CHEN Dian-ren, ZHAO Shuang. Multi-direction swath imaging and two-dimensional digital beamforming based on space-born hybrid phased-MIMO SAR. Journal of Jilin University Engineering and Technology Edition, 2016, 46(4): 1344-1353 复制到剪切板

Permissions

基于星载混合相控阵MIMO SAR的多方向测绘带成像及二维DBF处理

张乐乐, 陈殿仁, 赵爽

长春理工大学电子信息工程学院,长春 130022

通讯作者：陈殿仁 (1953-), 男,教授,博士生导师.研究方向:雷达信号处理,毫米波雷达技术,雷达目标模拟.E-mail:dianrenchen@163.com

作者简介:张乐乐(1987-),男,博士研究生.研究方向:高分辨率宽测绘带SAR成像技术.E-mail:andy_zhang1987@126.com

基金:国防装备预研项目(40405050302); 装备预研基金项目(9140A17010213Bq03003)

摘要

为解决图像模糊和图像混叠的问题,提出了将混合相控阵MIMO雷达与SAR相结合(混合相控阵MIMO SAR)的多方向测绘带成像方法,且提出二维数字波束合成(DBF)处理技术以实现无模糊宽测绘带高分辨率成像。首先建立该方法信号模型,推导了混合相控阵MIMO SAR的实际控制矩阵。然后针对多方向成像易造成图像混叠和距离模糊的不足,提出俯仰向自适应DBF算法,实现了图像混叠部分的有效分离且对模糊有很好的抑制。最后利用方位向加权对带外模糊置零。仿真结果表明该二维DBF处理技术的有效性。与星载双向和相控阵多向成像方法相比,该方法工作方式更灵活,能够满足多功能星载SAR的要求。

关键词: 信息处理技术; 星载混合相控阵MIMO SAR; 信号模型; 二维DBF; 图像混叠; 图像模糊

中图分类号:TN959.74 文献标志码:A 文章编号:1671-5497(2016)04-1344-10

Multi-direction swath imaging and two-dimensional digital beamforming based on space-born hybrid phased-MIMO SAR

ZHANG Le-le, CHEN Dian-ren, ZHAO Shuang

School of Electronics and Information Engineering, Changchun University of Science and Technology,Changchun 130022,China

Abstract

An imaging method of multi-direction swath based on space-born hybrid phased-MIMO SAR is proposed, which combines traditional phased-array radar with a new technique for multiple-input multiple-output (MIMO) radar, and the 2-D DBF for this system is presented to achieve unambiguous wide swath imaging with high azimuth resolution. Firstly, the signal model was built and the virtual control matrix of the Hybrid Phased-MIMO SAR was derived. Secondly, considering the image overlap and range ambiguity caused by multiple direction imaging, the adaptive Digital Beamforming (DBF) algorithm in range was proposed to separate the overlap area in images and to suppress the ambiguity. Finally, azimuth ambiguity that exceeds the signal bandwidth is suppressed by weighting in azimuth. Simulation results validate the effectiveness of this 2-D processing. Compared with space-born bi-direction SAR by two major lobes and multi-direction SAR by phased array, operation mode will be more flexible by using our method, and satisfy requests of multifunctional space-born SAR.

Keyword: information processing; space-born phased-MIMO SAR; signal model; 2-D BDF; image overlap; image ambiguity

Show Figures

0 引言

与传统的星载合成孔径雷达(SAR)相比, 新一代多功能星载合成孔径雷达能够在同一个卫星上完成不同的任务。这种雷达能够同时结合多种成像模式, 例如多波束ScanSAR、聚束成像、高分辨率宽带成像(HRWS)^{[1, 2]}等。在某些应用中要求对特定区域进行动态监测, 或者对特定运动目标进行速度测量和精确跟踪^[3], 这需要对不同方向的测绘带成像。文献[4]提出了星载双向SAR成像模型, 使方位向天线方向图的主瓣和栅瓣分别指向不同方向的目标区域, 并对其成像, 该方法受到天线的制约, 缺少灵活性, 不能同时在距离和方位向进行多方向测绘带成像。文献[5]提出了相控阵多功能成像雷达(PAMIR), 并对其系统设计和功能实现进行了研究。新一代的多输入多输出(MIMO)雷达系统中, 天线使用最新的多维波形编码技术^{[6, 7, 8, 9]}, 对发射信号进行独立选择, 灵活性高于传统的相控阵雷达系统。在此基础上, 文献[10-13]提出并研究了混合相控阵MIMO雷达(HMPAR), 它结合相控阵雷达和MIMO雷达的优点, 将发射阵列分为多个子阵列, 并使各个子阵列的发射信号相互正交, 经过发射波束合成指向任意方向。

本文将混合相控阵MIMO雷达与SAR相结合, 称为星载混合相控阵MIMO SAR(Hybrid phased-MIMO SAR), 提出基于星载混合相控阵MIMO SAR多方向测绘带成像方法, 其中高方位向分辨率和宽测绘带是多功能星载SAR的基本要求。文献[14]提出多通道无模糊重建算法, 利用方位向多通道接收技术^[15], 提高等效脉冲重复频率(PRF), 避免由于信号非均匀采样导致的方位模糊, 实现宽测绘带成像, 但是这种算法存在以下两个问题:①当回波为非带限信号时, 会造成图像模糊; ②在同一时刻, 多方向测绘带的部分反射回波信号会在接收端混叠, 造成图像混叠^[16]。

由于回波信号处于不同的距离单元和方位位置, 在俯仰向有不同的视角, 本文采用俯仰向DBF对回波信号进行自适应等副瓣加权并对模糊信号置零; 方位向DBF对带外模糊信号置零, 实现星载混合相控阵MIMO SAR的二维DBF, 不仅解决了图像模糊和图像混叠的问题, 还大大提升了系统的干扰抑制能力。

1 HMPAR原理

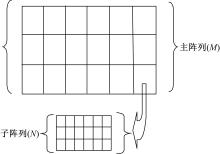
图1为混合相控阵MIMO雷达的一个矩形阵列, 又称 $\begin{matrix} MN \end{matrix}$ 阵列, 由 $\begin{matrix} M \end{matrix}$ 个子阵列组成, 每个子阵列由 $\begin{matrix} N \end{matrix}$ 个阵元构成。每个子阵列产生一个波束方向图照射 $\begin{matrix} 1 / M \end{matrix}$ 倍的总搜索范围, 通过形成 $\begin{matrix} M \end{matrix}$ 个恰当的波束, 就可以对整个搜索范围分配均匀的发射能量。如果 $\begin{matrix} M \end{matrix}$ 个子阵列的每个发射波束指向同一个方向, 则HMPAR是一个大型的相控阵雷达。这样的阵列根据不同应用的要求, 可以有多种配置方式, 这样发射波束方向图具有非常好的灵活性, 通常选择 $\begin{matrix} M = N, \end{matrix}$ 其发射方向图具有更高的灵活性, 配置方式如表1所示。

	Figure Option View Download New Window
	图1 混合相控阵MIMO雷达示意图Fig.1 Multi-direction SAR acquisition geometry

表1 HMPAR配置方式 Table 1 Possible rectangular configuration of HMPAR

HMPAR结合了相控阵雷达和MIMO雷达各自的优点, 通过分析各自的优点, 推导HMPAR发射信号的理论模型。假设发射信号矢量 $\begin{matrix} \tilde{s} (t) \end{matrix}$ 含 $\begin{matrix} M \end{matrix}$ 个相互正交的信号, $\begin{matrix} \tilde{s} (t) = {[\begin{matrix} {\tilde{s}}_{1} (t) & \dots & {\tilde{s}}_{M} (t) \end{matrix}]}^{T}, \end{matrix}$ 信号的协方差矩阵表示为:

$\begin{matrix} R (0) = \int_{T_{d}} \tilde{s} (t) {\tilde{s}}^{H} (t) dt = I_{M} (1) \end{matrix}$

式中: $\begin{matrix} I_{M} \end{matrix}$ 为一个 $\begin{matrix} M \times M \end{matrix}$ 的单位矩阵, 则 $\begin{matrix} M \end{matrix}$ 个子阵列的总发射能量为:

$\begin{matrix} E = tr \{\int_{T_{d}} \tilde{s} (t) {\tilde{s}}^{H} (t) dt\} = M (2) \end{matrix}$

式中:tr $\begin{matrix} \{\cdot\} \end{matrix}$ 表示矩阵的迹; $\begin{matrix} T_{d} \end{matrix}$ 为雷达脉冲的宽度; 第 $\begin{matrix} k \end{matrix}$ 个子阵列的发射信号定义为:

$\begin{matrix} s_{k} (t) = \sqrt[]{E_{k}} {\tilde{s}}_{k} (t) w_{k}^{*}, k = 1, 2, \dots, M (3) \end{matrix}$

式中: $\begin{matrix} w_{k} \end{matrix}$ 为第 $\begin{matrix} k \end{matrix}$ 个子阵列的波束合成加权复矢量, 其表达式为:

$\begin{matrix} w_{k} = \frac{a_{k} (θ_{k})}{‖ a_{k} (θ_{k}) ‖}, k = 1, 2, \dots, M (4) \end{matrix}$

式中: $\begin{matrix} E_{k} \end{matrix}$ 为第 $\begin{matrix} k \end{matrix}$ 个发射脉冲的能量, 表示为:

$\begin{matrix} E_{k} = \int_{T_{d}} {s^{H}}_{k} (t) s_{k} (t) dt = \frac{M}{M} = 1 \end{matrix}$ (5)

式中: $\begin{matrix} {(\cdot)}^{T} \end{matrix}$ 、 $\begin{matrix} {(\cdot)}^{H} \end{matrix}$ 、 $\begin{matrix} {(\cdot)}^{*} \end{matrix}$ 分别代表转置、厄米特转置和共轭算子。

对于 $\begin{matrix} M \end{matrix}$ 个子阵列, 如果每个子阵列的波束指向不同的方向, 对应的每个子阵列的控制矢量和HMPAR控制矢量矩阵分别为:

$\begin{matrix} \begin{matrix} a_{k} (θ_{k}) = \\ {[\begin{matrix} 1 & α & \dots & β \end{matrix}]}^{T} (6) \end{matrix} \end{matrix}$

式中: $\begin{matrix} α = e^{- j (2 π f_{0} dcos θ_{k} / c)}; β = e^{- j (2 π f_{0} (N - 1) dcos θ_{k} / c)} 。 \end{matrix}$ $\begin{matrix} A (θ) = [\begin{matrix} a_{1} (θ_{1}) & \dots & a_{M} (θ_{M}) \end{matrix}] (7) \end{matrix}$

式中: $\begin{matrix} θ_{k} \end{matrix}$ 表示第 $\begin{matrix} k \end{matrix}$ 个子阵列合成波束的指向; $\begin{matrix} d \end{matrix}$ 为每个子阵列中阵元之间的间距; $\begin{matrix} f_{0} \end{matrix}$ 为载波频率; $\begin{matrix} c \end{matrix}$ 为光速。

此系统叠加的发射信号为:

$\begin{matrix} y (t) = \overset{M}{\sum_{k = 1}} \sqrt[]{E_{k}} {\tilde{s}}_{k} (t) {w^{H}}_{k} a_{k} (θ_{k}) (8) \end{matrix}$

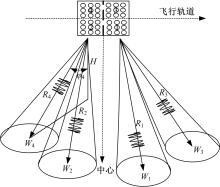
式(8)代表在同一时刻, 通过信号分集及空间复用的方法, $\begin{matrix} M \end{matrix}$ 个子阵列分别发射 $\begin{matrix} M \end{matrix}$ 个正交信号, 可以探测 $\begin{matrix} M \end{matrix}$ 个方向目标。

2 混合相控阵MIMO SAR多方向测绘带成像方法

图2为混合相控阵MIMO SAR多方向测绘带成像的示意图, 图2给出了配置4个子阵列的情形。在发射端, 把一个长脉冲分为间隔为 $\begin{matrix} T_{0} \end{matrix}$ 的4个相互正交的子脉冲, 每个子脉冲对应各自的子阵列, 依次发射不同方向的波束指向不同的测绘带。每个子脉冲分别对应不同的测绘带 $\begin{matrix} W_{k} \end{matrix}$ ^[17]如下:

$\begin{matrix} W_{k} = \frac{T_{k} c}{2 \sin φ_{k}} (9) \end{matrix}$

式中: $\begin{matrix} T_{k} c \end{matrix}$ 为每个子脉冲的长度; $\begin{matrix} c \end{matrix}$ 为光速; $\begin{matrix} φ_{k} \end{matrix}$ 为入射角。

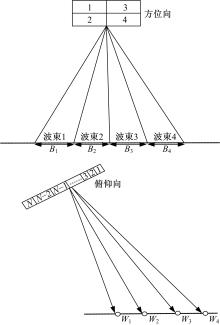
图3给出了4个子阵列的发射天线方向图, 实际应用中可以有多种配置方式。

	Figure Option View Download New Window
	图2 混合相控阵MIMO SAR多方向成像示意图Fig.2 Multi-direction SAR acquisition geometry

	Figure Option View Download New Window
	图3 混合相控阵MIMO SAR发射方向图Fig.3 Hybrid phased-MIMO SAR transmit beampattern

2.1 信号模型

假设第 $\begin{matrix} k \end{matrix}$ 个子阵列发送的信号如式(3)所示, 其中 $\begin{matrix} {\tilde{s}}_{k} (t) \end{matrix}$ 为线性调频信号:

$\begin{matrix} \begin{matrix} {\tilde{s}}_{k} (t) = rect [\frac{t - (k - 1) T_{0}}{T}] \times \\ \exp \{j 2 π f_{0} [t - (k - 1) T_{0}] + \\ jπ k_{r} {[t - (k - 1) T_{0}]}^{2} (10) \end{matrix} \end{matrix}$

式中:rect[ ]表示矩形函数; $\begin{matrix} k_{r} \end{matrix}$ 为线性调频信号的调斜率; $\begin{matrix} T \end{matrix}$ 为子脉冲持续时间。

利用点目标模型分析接收的原始数据, 假设每个测绘带对应不同斜距的点目标, 如图2所示, 每个点目标对应的斜距为 $\begin{matrix} R_{1}, R_{2}, \dots, R_{k}, \end{matrix}$ 它们之间满足如下关系:

$\begin{matrix} \{\begin{matrix} \frac{2 R_{1}}{c} = \frac{2 R_{2}}{c} + T_{0} \\ \frac{2 R_{2}}{c} = \frac{2 R_{3}}{c} + T_{0} \\ ︙ \\ \frac{2 R_{k - 1}}{c} = \frac{2 R_{k}}{c} + T_{0} \end{matrix} (11) \end{matrix}$

这些目标的回波信号将会在接收端产生混叠, 对于第 $\begin{matrix} k \end{matrix}$ 个点目标, 其回波信号为:

$\begin{matrix} \begin{matrix} s_{out_k} (t - 2 R_{k} / c) = \sqrt[]{E_{k}} {\tilde{s}}_{out_k} (t - \\ 2 R_{k} / c) w_{k}^{*} k = 1, 2, \dots, M (12) \\ {\tilde{s}}_{out_k} (t - 2 R_{k} / c) = \\ ρ_{t} rect [\frac{t - 2 R_{k} / c - (k - 1) T_{0}}{T}] \cdot \\ \exp \{j 2 π f_{0} [t - 2 R_{k} / c - (k - 1) T_{0}] + \\ jπ k_{r} {[t - 2 R_{k} / c - (k - 1) T_{0}]}^{2}\} (13) \end{matrix} \end{matrix}$

归纳总结式(11)可推得 $\begin{matrix} (2 R_{k}) / c = (2 R_{1}) / c - (k - 1) T_{0}, \end{matrix}$ 代入式(13)中得:

$\begin{matrix} \begin{matrix} {\tilde{s}}_{out_k} (t - 2 R_{k} / c) = ρ_{t} rect [\frac{t - 2 R_{1} / c}{T}] \cdot \\ \exp \{j 2 π f_{0} [t - 2 R_{1} / c] + \\ jπ k_{r} {[t - 2 R_{1} / c]}^{2}\} (14) \end{matrix} \end{matrix}$

式中: $\begin{matrix} ρ_{t} \end{matrix}$ 为目标反射信号的幅度, 每个子阵列 $\begin{matrix} j \end{matrix}$ 分别接收来自不同方向目标的反射信号, 其输出信号为:

$\begin{matrix} \begin{matrix} r_{j} (t - 2 R_{k} / c) = y (t - 2 R_{k} / c) a_{j} (θ_{k}) = \\ \overset{M}{\sum_{k = 1}} \sqrt[]{E_{k}} {\tilde{s}}_{out_k} (t - 2 R_{k} / c) \cdot \\ {w^{H}}_{k} a_{k} (θ_{k}) a_{j} (θ_{k}) (15) \end{matrix} \end{matrix}$

式中: $\begin{matrix} y (t - 2 R_{k} / c) \end{matrix}$ 为式(8)中 $\begin{matrix} y (t) \end{matrix}$ 的回波信号。

假设接收来自 $\begin{matrix} θ_{k} \end{matrix}$ 方向的目标回波信号, 则子阵列 $\begin{matrix} j \end{matrix}$ 接收的目标回波输出信号为:

$\begin{matrix} \begin{matrix} {\tilde{r}}_{j} (t - 2 R_{k} / c) = \sqrt[]{E_{k}} {\tilde{s}}_{out_k} (t - 2 R_{k} / c) {w^{H}}_{k} \cdot \\ a_{k} (θ_{k}) a_{j} (θ_{k}) (16) \end{matrix} \end{matrix}$

整理 $\begin{matrix} M \end{matrix}$ 个子阵列的接收信号为一个信号矢量 $\begin{matrix} r (θ_{k}) : \end{matrix}$

$\begin{matrix} \begin{matrix} r (θ_{k}) = [\begin{matrix} {\tilde{r}}_{1} (θ_{k}) \\ ︙ \\ {\tilde{r}}_{M} (θ_{k}) \end{matrix}] = \\ \sqrt[]{E_{k}} {\tilde{s}}_{out_k} (t - 2 R_{k} / c) A^{T} (θ_{k}) \otimes b (θ_{k}) = \\ \sqrt[]{E_{k}} {\tilde{s}}_{out_k} (t - 2 R_{k} / c) P (θ_{k}) (17) \end{matrix} \end{matrix}$

式中:􀱋表示克罗内克积, 其中 $\begin{matrix} b (θ_{k}) = {w^{H}}_{k} a_{k} (θ_{k}); P (θ_{k}) \end{matrix}$ 为混合相控阵MIMO SAR的实际控制矩阵, $\begin{matrix} P (θ_{k}) \end{matrix}$ 是一个 $\begin{matrix} N \times M \end{matrix}$ 阶矩阵, 如式(18)所示。

$\begin{matrix} \begin{matrix} P (θ_{k}) = \\ {[\begin{matrix} b (θ_{k}) & \dots & b (θ_{k}) \\ b (θ_{k}) e^{- j 2 π f_{0} dcos θ_{k} / c} & \dots & b (θ_{k}) e^{- j 2 π f_{0} \cos θ_{k} / c} \\ ︙ & ︙ \\ b (θ_{k}) e^{- j 2 π f_{0} (N - 1) dcos θ_{k} / c} & \dots & b (θ_{k}) e^{- j 2 π f_{0} (N - 1) dcos θ_{k} / c} \end{matrix}]}^{T} (18) \end{matrix} \end{matrix}$

通过恰当地选择 $\begin{matrix} P (θ_{k}) \end{matrix}$ 就可以实现混合相控阵MIMO SAR对不同方向测绘带成像, 接收 $\begin{matrix} θ_{k} \end{matrix}$ 方向的回波信号能量最大。由于要对多方向测绘带成像, 在回波信号中, 不仅存在严重的模糊信号, 还有子脉冲之间混叠的信号, 大大地降低了成像的质量。

2.2 二维DBF

混合相控阵MIMO SAR对回波信号分别采用俯仰向DBF和方位向DBF, 如图4所示, 方位向每个子阵列分别合成波束指向不同角度的测绘带, 方位向的角度分割等效于方位向多普勒带宽的分割, 每个波束分别对应一个窄带多普勒带宽 $\begin{matrix} B_{1} 、 B_{2} 、 B_{3} 、 B_{4}, \end{matrix}$ 与方位向多维波形编码等效。假设每个测绘带对应的点目标分别为 $\begin{matrix} W_{1} 、 W_{2} 、 W_{3} 、 W_{4}, \end{matrix}$ 在同一时间, 来自不同子脉冲的回波信号具有不同的俯仰角, 可以通过俯仰向DBF分离这些混叠雷达回波信号, 并对每个测绘带的信号进行俯仰向窄波束扫描接收(Narrow scan-on-receive), 最终无模糊分离方位向多个波束的回波信号, 方位向DBF对方位向模糊信号置零, 最后把这些回波信号相干结合后, 恢复出整个多普勒带宽并获得高方位向分辨率。本文采用的方法与多通道无模糊重建算法相比, 不仅能够恢复干净无模糊的频谱而且能够对模糊信号(距离模糊信号和方位向模糊信号)实现低旁瓣接收和模糊置零, 其中获取最优权数成为系统设计的关键。

	Figure Option View Download New Window
	图4 混合相控阵MIMO SAR方位向和俯仰向等效示意图Fig.4 Hybrid phased-MIMO SAR abridged general view in azimuth and range

2.2.1 俯仰向DBF

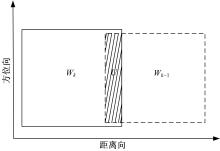
假设系统未对回波信号做加权处理, 子测绘带之间会发生混叠, 图5为信号混叠示意图, 第 $\begin{matrix} k \end{matrix}$ 个子脉冲对应测绘带 $\begin{matrix} W_{k}, \end{matrix}$ 第 $\begin{matrix} k - 1 \end{matrix}$ 个子脉冲对应测绘带 $\begin{matrix} W_{k - 1}, \end{matrix}$ 在最后输出的有效图像中出现混叠部分 $\begin{matrix} U 。 \end{matrix}$ 实际图形中还会有其他子测绘带之间的混叠部分和严重的模糊信号, 把这些信号统称为干扰信号(图5中未给出)。本文基于HMPAR给出一种俯仰向自适应DBF, 实现最优权数设计并对接收信号加权。

	Figure Option View Download New Window
	图5 信号混叠示意图Fig.5 Position of partially overlapped raw data blocks

假设干扰信号的幅度为 $\begin{matrix} {\{ρ_{m}\}}_{m = 1}^{B}, 位置为 {\{θ_{m}\}}_{m = 1}^{B}, \end{matrix}$ 则其回波信号可表示为:

$\begin{matrix} \begin{matrix} Q_{out_m} (t - 2 R_{m} / c) = \sqrt[]{E_{m}} ρ_{m} w_{m}^{*} rect [\frac{t - 2 R_{m} / c}{T}] \cdot \\ \exp \{j 2 π f_{0} [t - 2 R_{m} / c] + jπ k_{r} {[t - 2 R_{m} / c]}^{2}\} (19) \\ 式中 : \\ {\tilde{Q}}_{out_m} (t - 2 R_{m} / c) = ρ_{m} rect [\frac{t - 2 R_{m} / c}{T}] \cdot \\ \exp \{j 2 π f_{0} [t - 2 R_{m} / c]\} (20) \end{matrix} \end{matrix}$

则总接收信号如下:

$\begin{matrix} \begin{matrix} X (t) = r (θ_{k}) + \overset{B}{\sum_{m = 1}} z (θ_{m}) + n (t) = \\ \sqrt[]{E_{k}} {\tilde{s}}_{out_k} (t - 2 R_{k} / c) P (θ_{k}) + \end{matrix} \end{matrix}$

$\begin{matrix} \overset{B}{\sum_{m = 1}} \sqrt[]{E_{m}} {\tilde{Q}}_{out_m} (t - 2 R_{m} / c) P (θ_{m}) + n (t) (21) \end{matrix}$

式中: $\begin{matrix} z (θ_{m}) \end{matrix}$ 表示干扰信号的HMPAR输出信号矢量; $\begin{matrix} n (t) \end{matrix}$ 为HMPAR系统的噪声矢量, 由式(5)知 $\begin{matrix} E_{k} = E_{m} = 1 \end{matrix}$ 并带入式(21)中。

接收方向图要保证期望信号的增益最大, 干扰方向形成零点并且副瓣形状、增益与期望静态方向图接近, 设静态方向图综合得到的权为 $\begin{matrix} W_{0}, \end{matrix}$ 问题变为怎样使自适应方向图除了在干扰方向形成零点, 还具有静态方向图的特点, 比如低副瓣或特定形状的副瓣甚至固定零点等, 本文给出-40 dB的等副瓣。在保证满足线性最小方差约束法(LCMV)约束基础上, 使求出的权值尽量地逼近静态综合权 $\begin{matrix} W_{0}, \end{matrix}$ 设符合上面要求的自适应方向图控制权为 $\begin{matrix} W_{opt}, \end{matrix}$ 则 $\begin{matrix} W_{opt} \end{matrix}$ 为下面约束问题的解:

$\begin{matrix} \{\begin{matrix} \min_{W} W^{H} R_{XX} W \\ s . t . C^{H} W = f \end{matrix} (22) \end{matrix}$

式中: $\begin{matrix} R_{XX} \end{matrix}$ 为干扰加噪声的协方差矩阵;

$\begin{matrix} C \end{matrix}$ 为约束矩阵:

$\begin{matrix} C = [\begin{matrix} \bar{W_{0}} & \bar{C_{0}} & A (θ_{m}) \end{matrix}] (23) \end{matrix}$

式中: $\begin{matrix} \bar{C_{0}} \end{matrix}$ 是为了防止期望信号被自适应加权消除, 具体表达式参考文献[18]; $\begin{matrix} A (θ_{m}) \end{matrix}$ 为干扰信号的控制矢量。

$\begin{matrix} \bar{W_{0}} = \frac{W_{0}}{{W^{H}}_{0} W_{0}} (24) \end{matrix}$

$\begin{matrix} f \end{matrix}$ 设定 $\begin{matrix} C \end{matrix}$ 中每个列矢量对应的约束值:

$\begin{matrix} f = {[\begin{matrix} 1 & 0 & \dots & 0 \end{matrix}]}^{T} (25) \end{matrix}$

假设 $\begin{matrix} M \end{matrix}$ 元阵列, 有 $\begin{matrix} N \end{matrix}$ 个干扰, 为高斯白噪声背景, 噪声功率为 $\begin{matrix} σ_{n}^{2}, \end{matrix}$ 根据特征空间理论, 数据协方差阵 $\begin{matrix} R_{XX} \end{matrix}$ 的逆可表示为:

$\begin{matrix} \begin{matrix} R_{XX}^{- 1} = \overset{B}{\sum_{i = 1}} λ_{i}^{- 1} e_{i} {e^{H}}_{i} + \overset{N}{\sum_{i = B + 1}} σ_{n}^{- 2} e_{i} {e^{H}}_{i} = \\ σ_{n}^{- 2} [I - \overset{N}{\sum_{i = 1}} \frac{λ_{i} - σ_{n}^{2}}{λ_{i}} e_{i} {e^{H}}_{i}] (26) \end{matrix} \end{matrix}$

式中: $\begin{matrix} λ_{i} 、 e_{i} \end{matrix}$ 分别为 $\begin{matrix} R_{XX} \end{matrix}$ 的特征值和特征矢量。

为获得期望的自适应方向图并减少小特征值对应特征矢量的扰动, 采用对角加载技术^[19], 设加载量为 $\begin{matrix} Q 。 \end{matrix}$ 则最优权数可以表示为:

$\begin{matrix} \begin{matrix} W_{opt} = [I - \overset{N}{\sum_{i = 1}} \frac{λ_{i} + Q - σ_{n}^{2}}{λ_{i} + Q} e_{i} {e^{H}}_{i}] \bar{C} \cdot \\ {({\bar{C}}^{H} [I - \overset{N}{\sum_{i = 1}} \frac{λ_{i} + Q - σ_{n}^{2}}{λ_{i} + Q} e_{i} {e^{H}}_{i}] \bar{C})}^{- 1} f (27) \end{matrix} \end{matrix}$

则系统加权输出信号为:

$\begin{matrix} \begin{matrix} Y (t) = W_{opt}^{H} X (t) = \\ {\tilde{s}}_{out_k} (t - 2 R_{k} / c) W_{opt}^{H} P (θ_{k}) + \\ \overset{B}{\sum_{m = 1}} {\tilde{Q}}_{out_m} (t - 2 R_{m} / c) W_{opt}^{H} P (θ_{m}) + N (t) = \\ {\tilde{s}}_{out_k} (t - 2 R_{k} / c) U (θ_{k}) + \\ \overset{B}{\sum_{m = 1}} {\tilde{Q}}_{out_m} (t - 2 R_{m} / c) U (θ_{m}) + N (t) (28) \end{matrix} \end{matrix}$

式中: $\begin{matrix} U (θ_{k}) = {W^{H}}_{opt} P (θ_{k}) \end{matrix}$ 为期望信号的信道控制函数, 使得 $\begin{matrix} θ_{k} \end{matrix}$ 方向的回波信号能量能被最大接收; $\begin{matrix} U (θ_{m}) = W_{opt}^{H} P (θ_{m}) \end{matrix}$ 为干扰信号的信道控制函数, 可以有效地抑制 $\begin{matrix} θ_{m} \end{matrix}$ 方向的回波信号能量; $\begin{matrix} N (t) \end{matrix}$ 为系统加权后的噪声。

2.2.2 方位向DBF

回波信号通过俯仰向DBF对混叠信号进行分离并对模糊信号等副瓣抑制且置零, 这时虽然各个子脉冲的回波信号被无模糊分离, 但在方位向仍然存在模糊信号, 通过提高方位向多普勒带宽的采样频率(PRF)避免方位混叠, 但实际上多普勒频谱不是严格的带限, 这是由方位向天线方向图旁瓣引起的, 当回波的多普勒频率超出采样间隔-PRF/2≤ f_sig≤ PRF/2时, 这部分频率成分会被折叠进入当前处理的多普勒频率范围内, 从而产生模糊。

假设第 $\begin{matrix} P \end{matrix}$ 个子脉冲回波信号的多普勒带宽为 $\begin{matrix} - B_{p} / 2 \leq f_{sig} \leq B_{p} / 2, 其中 f_{sig} = 2 vsinφ / λ, v \end{matrix}$ 为卫星的飞行速度, $\begin{matrix} φ \end{matrix}$ 为方位斜视角, 则方位模糊的多普勒带宽为:

$\begin{matrix} \pm k \cdot PRF - B_{p} / 2 \leq f_{amb} \leq \pm k \cdot PRF + B_{p} / 2 (29) \end{matrix}$

式中: $\begin{matrix} f_{amb} = f_{sig} \pm k \cdot PRF; k \end{matrix}$ 为模糊信号阶数, 一阶模糊信号能量对总方位模糊能量贡献最大。

每个子脉冲对应的方位向加权矢量为 $\begin{matrix} W_{p} \end{matrix}$ , 通过方位向波束合成使多普勒模糊部分置零, 进而提取期望信号, 其表达式为:

$\begin{matrix} V_{p} W_{p} = H (30) \end{matrix}$

式中: $\begin{matrix} V_{p} \end{matrix}$ 为接收阵列矩阵, 矩阵中每行包含期望信号和模糊信号的控制矢量, $\begin{matrix} H = {[\begin{matrix} h_{1} & h_{2} & \dots & h_{n} \end{matrix}]}^{T}, \end{matrix}$ 其中 $\begin{matrix} h_{p} = 1, \end{matrix}$ 其他元素为零。由式(30)推导出 $\begin{matrix} W_{p} \end{matrix}$ 为:

$\begin{matrix} W_{p} = {V_{p}}^{- 1} H (31) \end{matrix}$

2.3 混合相控阵MIMO SAR多方向成像系统实现

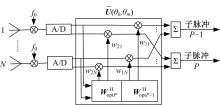
图6为基于混合相控阵MIMO SAR俯仰向DBF的系统框图, 假设发射 $\begin{matrix} P \end{matrix}$ 个子脉冲, 分别通过 $\begin{matrix} P \end{matrix}$ 个子阵列合成指向不同方向的波束, 照射 $\begin{matrix} P \end{matrix}$ 个子测绘带, 测绘带的回波信号被俯仰向 $\begin{matrix} N \end{matrix}$ 个子孔径同时接收。图6给出两个子测绘带分离的情况, 类似地, 对于超过两个子测绘带的分离情形在图6的基础上进行扩展。每个子孔径同时接收第 $\begin{matrix} P - 1 \end{matrix}$ 个子脉冲和第 $\begin{matrix} P \end{matrix}$ 个子脉冲的回波信号, 经过A/D变换后, 对输出两路信号分别加权, $\begin{matrix} W_{optP - 1}^{H} \end{matrix}$ 和 $\begin{matrix} W_{optP}^{H} \end{matrix}$ 为式(27)得到的最优权数, 分离出的两路信号各自累加输出。

	Figure Option View Download New Window
	图6 混合相控阵MIMO SAR俯仰向DBF系统框图Fig.6 Block diagram of system design in range

图6中 $\begin{matrix} \tilde{U} (θ_{k}, θ_{m}) \end{matrix}$ 为回波信号对应的系统信道控制函数, 如式(32)所示, 当 $\begin{matrix} k = m \end{matrix}$ 时, 为有用信号的信道控制函数; 当 $\begin{matrix} k \neq m \end{matrix}$ 时, 为干扰信号的信道控制函数。

$\begin{matrix} \tilde{U} (θ_{k}, θ_{m}) = \{\begin{matrix} U (θ_{k}), k = m \\ U (θ_{m}), k \neq m \end{matrix} (32) \end{matrix}$

	Figure Option View Download New Window
	图7 混合相控阵MIMO SAR方位向DBF系统框图Fig.7 Block diagram of system design in azimuth

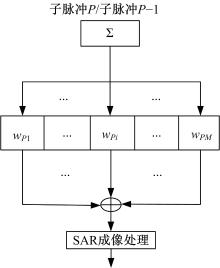
图7为方位向DBF系统框图, $\begin{matrix} M \end{matrix}$ 为方位向子孔径数, 子脉冲 $\begin{matrix} P \end{matrix}$ 和子脉冲 $\begin{matrix} P - 1 \end{matrix}$ 各自对应的回波信号通过方位向加权对方位模糊信号置零, 由式(31)得出权值, 加权后各子孔径输出信号叠加并进行SAR成像处理(例如RD算法)。

3 仿真分析

通过处理仿真点目标信号来验证本文的推导结果, 系统参数见表2。在实际应用中混合相控阵MIMO SAR有多种配置方式且有很好的灵活性, 本系统采用两个子阵列合成两个波束分别指向 $\begin{matrix} θ_{1} 、 θ_{2} \end{matrix}$ 方向, 发射方向图如图8所示。图9为混合相控阵MIMO SAR俯仰向双向发射天线方向图, 两个主波束的指向分别为34.78° 、40.96° 。

表2 混合相控阵MIMO SAR系统参数 Table 2 System parameters used in hybrid phased-MIMO SAR

	Figure Option View Download New Window
	图8 混合相控阵MIMO SAR发射方向图Fig.8 Hybrid phased-MIMO SAR transmit beampattern

	Figure Option View Download New Window
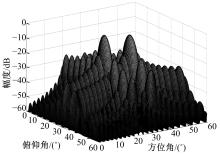
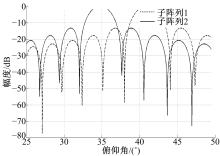	图9 混合相控阵MIMO SAR俯仰向双向发射方向图Fig.9 Hybrid phased-MIMO SAR bidirectional transmit beampattern in elevation

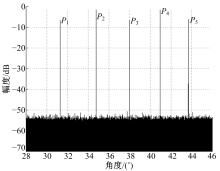
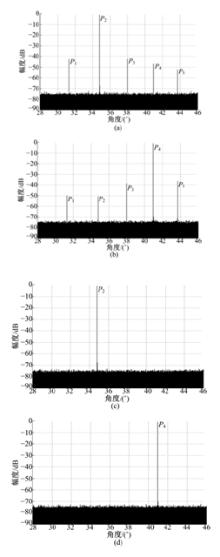
仿真中对每个子孔径加入白噪声, 信噪比为20 dB, 图10给出了原始距离像, 在回波信号中除了有两个子脉冲的混叠信号外, 还有距离模糊信号。其中 $\begin{matrix} P_{2} 、 P_{4} \end{matrix}$ 分别为两个子脉冲对应测绘带的点目标回波信号, 这是期望信号。 $\begin{matrix} P_{1} 、 P_{3} 、 P_{5} \end{matrix}$ 分别为其他测绘带的点目标回波信号, 这是仿真加入的距离模糊信号, 方向分别为31.28° 、38° 、43.68° , 这些信号会导致成像模糊。图11和图12给出了期望信号 $\begin{matrix} P_{2} 、 P_{4} \end{matrix}$ 方向的自适应波束合成接收方向图, 相比于传统的方法本文给出的俯仰向自适应DBF方法可以使接收方向图旁瓣接近于-40 dB且模糊信号深度置零。图13(a)、13(b)为传统零点指向方法对模糊信号的抑制结果, 低噪声时抑制性能明显。

	Figure Option View Download New Window
	图10 原始距离像Fig.10 Raw data with range compression

	Figure Option View Download New Window
	图11 θ ₁方向的自适应波束合成接收方向图Fig.11 Beampattern for direction θ ₁

	Figure Option View Download New Window
	图12 θ ₂方向的自适应波束合成接收方向图Fig.12 Beampattern for direction θ ₂

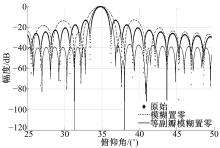
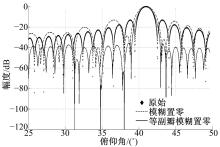
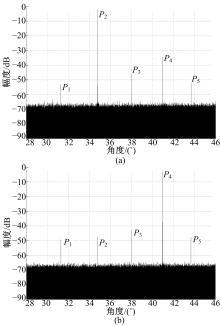
采用本文方法对回波信号自适应等副瓣接收, 分离出的期望信号如图14(a)、14(b)所示, 可以看出模糊信号平均幅度为-40 dB以下, 能够满足SAR的大部分应用要求, 如果对回波信号自适应等副瓣接收且对模糊信号置零, 由图14(c)、14(d)可以看到模糊信号不存在了, 其中噪声也得到了很好的抑制。

	Figure Option View Download New Window
	图13 传统零点指向法的点目标P₂与P₄距离像Fig.13 Range compression results of conventional null-steering method for point target P₂ and P₄

	Figure Option View Download New Window
	图14 本文方法的点目标P₂与P₄距离像Fig.14 Range compression results of advanced method for point target P₂ and P₄

当系统的信噪比为0 dB时, 从图15(a)、15(b)可看出传统零点指向法对噪声敏感, 其模糊信号的抑制性能下降明显。而本文方法的模糊抑制性能与信噪比为20 dB时一致, 模糊信号被完全消除, 如图15(c)、15(d)所示。

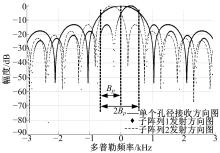
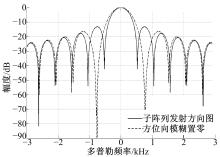
	Figure Option View Download New Window
	图15 系统信噪比为0 dB时的性能比较Fig.15 Performance comparison at SNR=0 dB

图16为方位向天线方向图, 单个发射波束的多普勒带宽为 $\begin{matrix} B_{P}, \end{matrix}$ 由图可以看出单个孔径接收方向图的等效多普勒带宽为 $\begin{matrix} 2 B_{P} \end{matrix}$ , 其带宽是两个发射波束的相干结合, 多普勒带宽内还存在一阶方位模糊, 其与发射波束旁瓣相对应。分离后的回波信号经过方位向加权后, 如图17所示, 天线方向图的第一旁瓣被深度置零, 抑制了带外信号。

	Figure Option View Download New Window
	图16 方位向天线方向图Fig.16 Beampattern in azimuth

	Figure Option View Download New Window
	图17 方位向加权Fig.17 Beampattern with beamforming in azimuth

4 结束语

提出了星载混合相控阵MIMO SAR多方向测绘带成像方法, 同时给出了基于此系统的二维DBF处理技术。分别对回波信号进行俯仰向DBF处理, 与传统零点指向法相比, 本文方法对噪声不敏感, 能够分离出混叠的子脉冲信号且抑制模糊信号。同时对子脉冲信号在方位向加权, 抑制方位向带外模糊信号。仿真结果表明:本文提出的二维DBF处理技术不仅能无模糊分离期望信号且对干扰信号进行了有效抑制, 能够输出无模糊高分辨率的多方向图像。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Gebert N, Krieger G, Moreira A. Multichannel azimuth processing in ScanSAR and TOPS mode operation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(7): 2994-3008. [本文引用:1]
[2]	Gao Can-guan, Wang R, Deng Yun-kai, et al. Large-scene sliding spotlight SAR using multiple channels in azimuth[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(5): 1006-1010. [本文引用:1]
[3]	Henke D, Magnard C, Frioud M, et al. Moving-target tracking in single-channel wide-beam SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(11): 4735-4747. [本文引用:1]
[4]	Wollstadt S, Prats-Iraola P, Lopez-Dekker P, et al. Bidirectional SAR imaging mode[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(1): 601-614. [本文引用:1]
[5]	Ender J H G, Brenner A R. PAMIR—a wideband phased array SAR/MTI system[J]. IEE Proceedings Radar, Sonar and Navigation, 2003, 150(3): 165-172. [本文引用:1]
[6]	Wang Wen-qin. MIMO SAR OFDM chirp waveform diversity design with rand om matrix modulation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(3): 1615-1625. [本文引用:1]
[7]	Kim J H, Younis M, Prats-Iraola P, et al. First spaceborne demonstration of digital beamforming for azimuth ambiguity suppression[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(1): 1-11. [本文引用:1]
[8]	Krieger G, Gebert N, Moreira A. Multidimensional waveform encoding: a new digital beamforming technique for synthetic aperture radar remote sensing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(1): 31-46. [本文引用:1]
[9]	Feng Fan, Li Shi-qiang, Yu Wei-dong, et al. Study on the processing scheme for space-time waveform encoding SAR system based on two-dimensional digital beamforming[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(3): 910-932. [本文引用:1]
[10]	Hassanien A, Vorobyov S A. Phased-MIMO radar: a tradeoff between phased-array and MIMO radars[J]. IEEE Transactions on Signal Processing, 2010, 58(6): 1-33. [本文引用:1]
[11]	Fuhrmann D R, Browning J P, Rangaswamy Muralidhar. Signaling strategies for the hybrid MIMO phased-array radar[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(1): 66-78. [本文引用:1]
[12]	Hua G, Abeysekera S S. Receiver design for range and doppler sidelobe suppression using MIMO and phased-array radar[J]. IEEE Transactions on Signal Processing, 2013, 61(6): 1315-1326. [本文引用:1]
[13]	Wang Wen-qin, Shao Huai-zong. A flexible phased-MIMO array antenna with transmit beamforming[J]. International Journal of Antennas and Propagation, 2012, 10(6): 473-475. [本文引用:1]
[14]	Krieger G, Gebert N, Moreira A. Unambiguous SAR signal reconstruction from nonuniform displaced phase center sampling[J]. IEEE Geoscience and Remote Sensing Letters, 2004, 1(4): 260-264. [本文引用:1]
[15]	Wang Wen-qin. High altitude platform multichannel SAR for wide-area and staring imaging[J]. IEEE A&E Systems Magazine, 2014, 29(5): 12-17. [本文引用:1]
[16]	冯帆, 李世强, 禹卫东. 一种多维编码全极化SAR回波分离改进方法[J]. 电子与信息学报, 2012, 34(1): 172-178. Feng Fan, Li Shi-qiang, Yu Wei-dong. An improved approach to separating echoes in multidimensional waveform encoding fully-polarimetric SAR[J]. Journal of Electronics&Information Technology, 2012, 34(1): 172-178. [本文引用:1]
[17]	Kou Guang-jie, Wang Zhen-song, Yao Ping. Multiple beams spaceborne SAR imaging[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(4): 3363-3375. [本文引用:1]
[18]	Tseng C Y, Griffiths L J. A unified approach to the design of linear constraints in minimum variance adaptive beamformers[J]. IEEE Transactions on Antennas and Propagation, 1992, 40(12): 1533-1542. [本文引用:]
[19]	Carlson B D. Covariance matrix estimation errors and diagonal loading in adaptive arrays[J]. IEEE Transactions on Aerospace and Electronic Systems, 1988, 24(4): 397-401. [本文引用:1]

2010

0.0

... 这种雷达能够同时结合多种成像模式,例如多波束ScanSAR、聚束成像、高分辨率宽带成像(HRWS)^[1,2]等 ...

2013

0.0

... 这种雷达能够同时结合多种成像模式,例如多波束ScanSAR、聚束成像、高分辨率宽带成像(HRWS)^[1,2]等 ...

2012

0.0

... 在某些应用中要求对特定区域进行动态监测,或者对特定运动目标进行速度测量和精确跟踪^[3],这需要对不同方向的测绘带成像 ...

2013

0.0

... 文献[4]提出了星载双向SAR成像模型,使方位向天线方向图的主瓣和栅瓣分别指向不同方向的目标区域,并对其成像,该方法受到天线的制约,缺少灵活性,不能同时在距离和方位向进行多方向测绘带成像 ...

2003

0.0

... 文献[5]提出了相控阵多功能成像雷达(PAMIR),并对其系统设计和功能实现进行了研究 ...

2015

0.0

... 新一代的多输入多输出(MIMO)雷达系统中,天线使用最新的多维波形编码技术^[6,7,8,9],对发射信号进行独立选择,灵活性高于传统的相控阵雷达系统 ...

2013

0.0

... 新一代的多输入多输出(MIMO)雷达系统中,天线使用最新的多维波形编码技术^[6,7,8,9],对发射信号进行独立选择,灵活性高于传统的相控阵雷达系统 ...

2008

0.0

... 新一代的多输入多输出(MIMO)雷达系统中,天线使用最新的多维波形编码技术^[6,7,8,9],对发射信号进行独立选择,灵活性高于传统的相控阵雷达系统 ...

2012

0.0

... 新一代的多输入多输出(MIMO)雷达系统中,天线使用最新的多维波形编码技术^[6,7,8,9],对发射信号进行独立选择,灵活性高于传统的相控阵雷达系统 ...

2010

0.0

2010

0.0

2013

0.0

2012

0.0

2004

0.0

... 文献[14]提出多通道无模糊重建算法,利用方位向多通道接收技术^[15],提高等效脉冲重复频率(PRF),避免由于信号非均匀采样导致的方位模糊,实现宽测绘带成像,但是这种算法存在以下两个问题:①当回波为非带限信号时,会造成图像模糊 ...

2014

0.0

2012

0.0

. 2012, 34(1):172-178 DOI:doi:10.3724/SP.J.1146.2011.00279

An improved approach to separating echoes in multidimensional waveform encoding fully-polarimetric SAR

一种多维编码全极化SAR回波分离改进方法

Feng Fan , Li Shi-qiang , Yu Wei-dong.

冯帆, 李世强, 禹卫东

By emitting H- and V-polarized pulses adjacently and receiving echoes with duo-polarized channels, multidimensional waveform encoding fully-polarimetric Synthetic Aperture Radar (SAR) can obtain all polarimetric components in one Pulse Repetition Interval (PRI). However, different polarized echoes will overlap under this mode, and thus should be separated effectively to realize fully-polarimetric remote sensing. To solve this problem, this paper proposes a new elevation Digital BeamForming (DBF) approach, which systematically integrates Finite Impulse Response (FIR) filters into the -steering beamformer, to separate echoes. Compared with conventional -steering beamfoming, FIR filters in the approach can deal with the issue of pulse extension well, thereby achieving better separation results. In the paper, detailed signal processing procedures, along with the block diagram of the new DBF, are provided. Simulation results are given to demonstrate the validation of the proposed approach.

通过依次发射H与V极化脉冲和双极化通道接收回波，多维编码全极化SAR能在一个脉冲重复间隔(PRI)内获得所有极化分量。然而，该模式下不同的极化回波会发生混叠，因此需要将它们有效分离开。该文提出了一种将FIR时域滤波处理嵌入到零点指向波束形成器的新型俯仰向数字波束形成(DBF)方法来分离回波。与传统零点指向法相比，该文方法中的FIR滤波能够解决脉冲空域延展所带来的问题，从而取得更好的分离效果。文中给出了详细的信号处理流程及新型波束形成器系统框图。仿真结果验证了该方法的有效性。

... ②在同一时刻,多方向测绘带的部分反射回波信号会在接收端混叠,造成图像混叠^[16] ...

2012

0.0

... 每个子脉冲分别对应不同的测绘带 Wk^[17]如下: ...

1992

1988

0.0

... 为获得期望的自适应方向图并减少小特征值对应特征矢量的扰动,采用对角加载技术^[19],设加载量为 Q ...