基于改进加权质心和UKF的移动目标定位算法

引用本文

许杰, 戚大伟. 基于改进加权质心和UKF的移动目标定位算法.吉林大学学报:工学版, 2016, 46(4): 1354-1359
XU Jie, QI Da-wei. Moving target localization based on improved weighted centroid and UKF algorithm. Journal of Jilin University Engineering and Technology Edition, 2016, 46(4): 1354-1359 复制到剪切板

Permissions

基于改进加权质心和UKF的移动目标定位算法

许杰^1,², 戚大伟³

1.黑龙江八一农垦大学信息技术学院,黑龙江大庆163319

2.东北林业大学工程技术学院, 哈尔滨 150040

3.东北林业大学理学院, 哈尔滨 150040

作者简介:许杰(1973),男,副教授,博士.研究方向:数字图像处理及农业(林业)信息化.E-mail:byndxj@163.com

基金:国家自然科学基金项目(31170518); 黑龙江省科技攻关项目(GC01KC156); 黑龙江省教育厅科研项目(12531445)

摘要

为了解决传统算法对于移动目标定位误差较大的问题,提出了一种基于接受信号强度指示(RSSI)的改进加权质心定位算法,并结合一种改进的UKF算法对RSSI进行有效滤波。针对传统质心定位算法只能静态设置权重的缺陷,提出利用定位误差对距离进行修正,有效提高了算法的定位精度。对于标准UKF算法,在采样过程中采用改进最小偏度策略,引入调节因子,保证了预测方差矩阵的半正定性,并且在滤波更新过程中采用衰减记忆滤波方法,有效抑制了滤波发散,提高了滤波精度。仿真实验结果证明了本文算法的正确性和有效性。

关键词: 信息处理技术; 移动目标定位; 加权质心算法; 无迹卡尔曼滤波

中图分类号:TN911 文献标志码:A 文章编号:1671-5497(2016)04-1354-06

Moving target localization based on improved weighted centroid and UKF algorithm

XU Jie^1,², QI Da-wei³

1.College of Information Technology, Heilongjiang Bayi Agricultural University, Daqing 163319,China

2.College of Engineering and Technology, Northeast Forestry University, Harbin 150040,China

3.College of Science, Northeast Forestry University, Harbin 150040,China

Abstract

Using traditional localization algorithms the location error is high for moving target. To solve this problem, an improved weighted centroid localization algorithm based on Received Signal Strength Intensity (RSSI) is proposed, and an improved Unscented Kalman Filter (UFK) algorithm is combined for RSSI filtering. For the defect that traditional centroid localization algorithm can only statically set the weights, in this improved algorithm, the localization error is used to correct the distance, which can effectively improves the localization accuracy. For the standard UKF algorithm, the minimum skewness strategy is used in the sampling process, and the adjustment factors are introduced to ensure the positive semidefinite of the prediction covariance matrix; simultaneously, the fading memory filtering method is used in filter updating process, which effectively inhibits the filter divergence and improves the filtering accuracy. Simulation results prove the correctness and effectiveness of the proposed algorithm.

Keyword: information processing; moving target localization; weighted centroid algorithm; unscented Kalman filter(UKF)

Show Figures

0 引言

许多的工程应用都需要对移动目标进行实时定位, 以便获得目标的动态信息, 从而进行后续处理。通常情况下, 移动目标都是依靠自身的传感器采集信息, 然后通过无线方式与路由节点通信来实现定位。受现场环境等因素的制约, 定位精度常常无法满足要求, 在硬件设备无法提升定位精度的情况下, 只能寻求更为先进的定位算法^{[1, 2, 3]}。

目前的移动目标定位算法主要分为两大类:第一类是不依靠距离的定位算法, 包括质心算法、凸规划算法以及DV-HOP算法等^{[4, 5]}; 第二类是基于距离的定位算法, 主要包括三边测量算法、三角测量算法以及极大似然估计算法等^{[6, 7]}。这两类方法各有优缺点, 因此经常会被结合使用, 在保证定位精度的前提下, 尽量降低硬件成本。

接收信号强度指示(Received signal strength indicator, RSSI)是一种用于计算节点间相对距离的常用参数, 不需要其他硬件, 可直接从移动目标自身携带的传感器获得。基于RSSI的加权质心定位算法在多个领域中都有应用, 并且取得了一定的效果^[8]。但是传统加权质心定位算法在分配权重时只是单纯地考虑与距离成反比关系, 存在一定的不合理性。此外, 在实际的测量环境中, RSSI很容易受到外界干扰, 混入一定的噪声, 就会导致数据出现较大的随机性和误差, 因此需要对RSSI进行有效滤波。

基于上述分析, 本文首先提出了一种改进的基于RSSI的加权质心定位算法, 该算法引入反馈机制, 利用定位误差对距离进行修正, 从而实现权重的动态调整; 其次, 利用UKF算法对获得的RSSI进行滤波, 针对传统UKF算法复杂度高的缺点, 通过优化最小偏度单形采样策略减少采样点, 以衰减记忆滤波平方根替代协方差阵实现递推运算, 从而减少计算误差引起的滤波发散, 达到改进UKF算法性能的目的。仿真实验结果表明, 本文算法具有较好的性能以及较高的定位精度。

1 移动目标定位算法

1.1 基于RSSI的加权质心定位算法

传统的质心算法原理为:当未知节点在定位区域中移动时, 通过广播方式与锚节点进行通信, 当收集到所有能与之连通的锚节点信息后, 计算出覆盖区域重叠部分的中心, 即估计未知节点的位置。从传统质心定位算法的原理可知, 能够给未知节点提供信息的锚节点越多, 定位越准确, 但是在实际应用中并不会有足够数量的锚节点来保障该算法的精度。此外, 传统质心算法不能保证未知节点从锚节点处接收的信息量相同, 当这些信息的方差较大时, 定位精度同样会受到很大影响。总体来看, 传统质心算法只能用于初步定位。

一种对质心算法的有效改进措施就是引入距离信息, 使未知节点与锚节点之间的位置有可参考的依据。在一个节点网络中, 发送节点广播的信息中会包含发射功率值, 而接收节点通过比较接收到信号的功率与自身的发射功率计算出功率差, 再通过某种信号传播模型计算出节点间的距离, 这就是RSSI的原理。因此可以定义RSSI为:

$\begin{matrix} RSSI = 10 * \lg \frac{P'_{rs}}{P_{ref}} (1) \end{matrix}$

式中: $\begin{matrix} P_{ref} \end{matrix}$ 为参考功率。如果信号传播的空间为理想自由空间, 那么 $\begin{matrix} P_{rs} = P'_{rs}, \end{matrix}$ 根据费尔斯电波公式:

$\begin{matrix} P_{rs} = P_{ts} \times G_{ts} \times G_{rs} * {(\frac{λ}{4 π d_{ij}})}^{2} (2) \end{matrix}$

式中: $\begin{matrix} P_{rs} \end{matrix}$ 为接收功率; $\begin{matrix} P_{ts} \end{matrix}$ 为发送功率; $\begin{matrix} G_{rs} \end{matrix}$ 为接收增益; $\begin{matrix} G_{ts} \end{matrix}$ 为发送增益; $\begin{matrix} λ \end{matrix}$ 为波长; $\begin{matrix} d_{ij} \end{matrix}$ 为发送节点与接收节点之间的距离。

由RSSI的原理可以看出, 其与距离之间存在特定的对应关系, 当其他参数已知时, 就可以利用RSSI计算出距离, 并且RSSI与距离之间呈明显的反比关系。与未知节点越近的锚节点其权重应该越大, 因此引入距离以后, 加权质心算法为:

$\begin{matrix} x = \frac{\overset{n}{\sum_{i = 1}} \frac{x_{i}}{d_{i}}}{\overset{n}{\sum_{i = 1}} \frac{1}{d_{i}}}, y = \frac{\overset{n}{\sum_{i = 1}} \frac{y_{i}}{d_{i}}}{\overset{n}{\sum_{i = 1}} \frac{1}{d_{i}}} (3) \end{matrix}$

1.2 改进的加权质心定位算法

由于距离信息参与了定位计算, 基于RSSI的加权质心算法的定位精度明显高于传统质心算法。但是RSSI非常容易受到外界干扰, 即使是同一个节点, 在同一个位置的发射功率也存在跳变现象, 因此完全依靠RSSI计算的权重并不能很好地根据情况变化进行调整, 导致定位结果稳定性不高。

针对上述问题, 本文提出一种改进的加权质心定位算法, 借鉴控制理论中的反馈思想, 计算每一次算法定位后的误差, 如果误差超过给定阈值, 则对利用RSSI计算出的距离进行动态修正; 否则, 距离不做改动。那么这里存在一个问题, 即如何实时地判定一次定位结果是否满足误差要求。理论上, 应该通过计算真实坐标与算法定位坐标之间的均方误差, 但是实际情况中并不知道未知节点的真实坐标, 所以直接计算定位误差的方式无法实现, 故本文采取一种间接方式来计算误差。现在能够得到的信息包括:通过RSSI计算得到的未知节点与锚节点之间的距离 $\begin{matrix} {d_{1}, d_{2}, \dots, d_{n}} \end{matrix}$ , 通过定位算法计算出的估计位置与锚节点之间的距离 $\begin{matrix} {d'_{1}, d'_{2}, \dots, d'_{n}}, \end{matrix}$ 那么定位误差可以定义为:

$\begin{matrix} ΔE = \sqrt[]{\frac{1}{n} \overset{n}{\sum_{i = 1}} {(d_{i} - d'_{i})}^{2}} (4) \end{matrix}$

根据式(4), 距离的动态调整公式为:

$\begin{matrix} d_{i + 1} = \{\begin{matrix} d_{i} + ΔE, ΔE \geq t h r \\ d_{i}, 其他 \end{matrix} (5) \end{matrix}$

式中:thr为根据经验给定的阈值, 通常情况下, 质心算法的定位误差大约为2 m, 根据三角形定理, 即三角形两边之差要小于第三边, 所以thr应该小于2 m, 再考虑到通过RSSI计算距离存在一定的误差, 所以本文建议thr取值范围为1~1.5 m。

1.3 改进定位算法的实现步骤

本文提出的改进加权质心定位算法的实现步骤为:

步骤1 锚节点周期性地向相邻节点广播发送自身信息, 包括节点ID和位置坐标。

步骤2 按照事先设定的数量 $\begin{matrix} n \end{matrix}$ , 未知节点接收锚节点发送的RSSI, 并且每一个锚节点只接收一个RSSI。

步骤3 根据式(1)(2)计算出未知节点与锚节点之间基于RSSI的距离集合 $\begin{matrix} {d_{1}, d_{2}, \dots, d_{n}} 。 \end{matrix}$

步骤4 通过加权质心算法计算出未知节点的位置估计值 $\begin{matrix} (x', y'), \end{matrix}$ 进而计算出位置估计值与锚节点之间的距离集合 $\begin{matrix} {d'_{1}, d'_{2}, \dots, d'_{n}} 。 \end{matrix}$

步骤5 根据式(4)(5)对距离进行调整修正。

步骤6 重复步骤(4)和步骤(5), 直到定位误差满足要求为止。

2 改进的UKF算法

在未知节点接收锚节点信息的过程中, 除了由于自身传感器原因而造成的发射功率跳变以外, 传输环境和信道能量等原因也会引起RSSI的随机变化, 混入大量噪声, 从而导致所计算的距离存在较大误差, 因此必须对得到的RSSI进行有效滤波。

UKF算法是一种非线性滤波算法, 其原理是利用采样策略逼近函数的非线性分布。该算法的最大优点是无需计算系统方程的雅克比矩阵, 因此其计算复杂度要明显低于KF、EKF等算法, 而且滤波精度也较高。UKF算法也存在如下的缺陷:首先, 目前经常采用的Sigma点采样策略基本都是对称采样, 在这个过程中, 需要 $\begin{matrix} L = 2 n + 1 \end{matrix}$ 个Sigma点, 对如此数量的Sigma点进行UT变换, 计算量太大, 无法应用于对实时性要求较高的系统中; 其次, 采用UKF算法进行滤波计算时, 经常存在发散现象, 尤其是测量值数目逐渐增多时, 按滤波方程计算的估计均方误差矩阵会趋于零或某一稳态值, 但估计值与真实值之间的偏差却越来越大, 最终导致滤波器失效。

针对上述问题, 本文提出两种改进措施:在Sigma采样过程中, 采用改进的最小偏度采样策略, 有效降低算法计算量, 提高实时性; 采用衰减记忆法滤波逐渐减小原来测量值的权重, 有效降低测量值对估计值的影响, 实现对滤波发散的有效抑制。

考虑一个一般的非线性模型:

$\begin{matrix} \begin{matrix} x_{k} & = f_{k - 1} (x_{k - 1}) + w_{k - 1} (6) \\ z_{k} & = h_{k} (x_{k}) + v_{k} (7) \end{matrix} \end{matrix}$

式中: $\begin{matrix} x_{k} \in R^{n} \end{matrix}$ 为系统状态; $\begin{matrix} f_{k} \in R^{n} \end{matrix}$ 和 $\begin{matrix} h_{k} \in R^{m} \end{matrix}$ 为系统状态的函数; 系统噪声 $\begin{matrix} w_{k} \in R^{n} \end{matrix}$ 和量测噪声 $\begin{matrix} v_{k} \in R^{m} \end{matrix}$ 为互不相关的零均值白噪声, 对应的协方差矩阵分别为 $\begin{matrix} Q_{k} \end{matrix}$ 和 $\begin{matrix} R_{k} 。 \end{matrix}$

改进UKF滤波算法的实现过程为:

(1)算法初始化

初始状态 $\begin{matrix} x_{0} \end{matrix}$ 要独立于所有噪声, 其先验均值和协方差阵为:

$\begin{matrix} E (x_{0}) = {\bar{x}}_{0} = {\hat{x}}_{0 | 0}, cov (x_{0}) = P_{0} (8) \end{matrix}$

(2)Sigma点集及其权系数生成

选择 $\begin{matrix} 0 \leq W_{0} < 1, \end{matrix}$ 则Sigma点权值为:

$\begin{matrix} W_{i} = \{\begin{matrix} (1 - W_{0}) / 2^{n}, i = 1 \\ W_{1}, i = 2 \\ 2^{i - 1} \times W_{1}, i = 3 \end{matrix} (9) \end{matrix}$

(3)初始向量迭代

输入状态为1维时:

$\begin{matrix} \{\begin{matrix} x_{0}^{1} = [0] \\ x_{1}^{1} = [- 1 / \sqrt[]{2 * W_{1}}] \\ x_{2}^{1} = [1 / \sqrt[]{2 * W_{1}}] \end{matrix} (10) \end{matrix}$

输入状态大于1维时:

$\begin{matrix} x_{i}^{j + 1} = \{\begin{matrix} [\begin{matrix} x_{i}^{j} \\ 0 \end{matrix}], i = 0 \\ [\begin{matrix} x_{i}^{j} \\ - 1 / \sqrt[]{2 * W_{j + 1}} \end{matrix}], i = 1, 2, \dots, j \\ [\begin{matrix} 0 \\ 1 / \sqrt[]{2 * W_{j + 1}} \end{matrix}], i = j + 1 \end{matrix} (11) \end{matrix}$

(4)嵌入均值和协方差信息

$\begin{matrix} x_{i} = \bar{x} + (\sqrt[]{P_{x}}) \times x_{i}^{j} (12) \end{matrix}$

从上述的采样策略可以看出, 其无法保证预测方差矩阵的半正定性, 本文通过引入调节因子的方法来解决这一问题, 如下所示:

$\begin{matrix} W_{i}^{(m)} = \{\begin{matrix} (1 - W_{0}) / (2^{n} \times ε^{2}), i = 1, 2 \\ (2^{i - 1} \times W_{1}) / ε^{2}, i = 3, 4, \dots, n + 1 \end{matrix} (13) \end{matrix}$

(5)时间方程更新

$\begin{matrix} \begin{matrix} \begin{matrix} x_{k}^{(i)} & = f (x_{i}) + U (k), i = 0, 1, \dots, 2 n (14) \\ {\hat{x}}_{k, k - 1} & = \overset{2 n}{\sum_{i = 0}} w_{i} x_{k}^{(i)} (15) \end{matrix} \\ P_{k, k - 1} = \overset{2 n}{\sum_{i = 0}} w_{i} [x_{k}^{(i)} - {\hat{x}}_{k, k - 1}] {[x_{k}^{(i)} - {\hat{x}}_{k, k - 1}]}^{T} + \\ Q_{k} s^{N - k}, s > 1 (16) \end{matrix} \end{matrix}$

(6)测量方程更新

$\begin{matrix} \begin{matrix} z_{k, k - 1}^{(i)} & = h ({\hat{x}}_{k, k - 1}^{(i)}) (17) \\ {\hat{z}}_{k, k - 1} & = \overset{2 n}{\sum_{i = 0}} w_{i} z_{k, k - 1}^{(i)} (18) \end{matrix} \end{matrix}$

(7)计算滤波增益

$\begin{matrix} \begin{matrix} P_{zz} = \overset{2 n}{\sum_{i = 0}} w_{i} [z_{k, k - 1}^{(i)} - {\hat{z}}_{k, k - 1}] {[z_{k, k - 1}^{(i)} - {\hat{z}}_{k, k - 1}]}^{T} + \\ R_{k} s^{N - k}, s > 1 (19) \\ P_{x z} = \overset{2 n}{\sum_{i = 0}} w_{i} [x_{k, k - 1}^{(i)} - {\hat{x}}_{k, k - 1}] {[z_{k, k - 1}^{(i)} - {\hat{z}}_{k, k - 1}]}^{T} (20) \\ K_{k} = P_{xz} P_{zz}^{- 1} (21) \end{matrix} \end{matrix}$

从式(16)和式(19)可以看出, 本文利用衰减记忆方法对噪声统计模型进行了改进, 分别用 $\begin{matrix} R_{k} s^{N - k} \end{matrix}$ 和 $\begin{matrix} Q_{k} s^{N - k} \end{matrix}$ 替代了原来的 $\begin{matrix} R_{k} \end{matrix}$ 和 $\begin{matrix} Q_{k}, \end{matrix}$ 即在右侧添加了一个标量因子。这样改进以后, 当前时刻测量值的权值增大, $\begin{matrix} N \end{matrix}$ 时刻以前的观测值逐渐衰减, 使以前时刻测量值对估计值的影响变小, 有效抑制了滤波发散。

3 实验分析

3.1 UKF滤波算法性能比较

根据经验, 同一地点RSSI的变化不大, 因此可建立关于RSSI的状态空间方程如下:

$\begin{matrix} \{\begin{matrix} x_{k} = x_{k - 1} + w_{k} \\ z_{k} = x_{k} + v_{k} \end{matrix} (22) \end{matrix}$

式中:状态 $\begin{matrix} x_{k} \end{matrix}$ 即为RSSI; 系统噪声 $\begin{matrix} w_{k} \end{matrix}$ 和量测噪声 $\begin{matrix} v_{k} \end{matrix}$ 根据多次试验分别取为均值为0、噪声方差为0.09和0.47的白噪声。

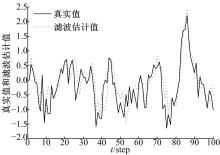
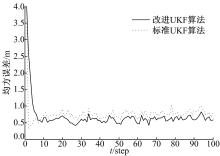
利用改进UKF算法对RSSI进行滤波, 考查滤波估计值与RSSI真实值之间的跟踪效果, 如图1所示。在同样条件下, 进行100次蒙特卡罗实验, 比较两种算法对RSSI滤波的估计值与真实值之间的均方误差, 结果如图2所示。

	Figure Option View Download New Window
	图1 滤波估计值与真实值跟踪图Fig.1 Filter and true value tracking graph

	Figure Option View Download New Window
	图2 滤波均方误差比较Fig.2 Comparison of mean square error filter

从图1和图2的结果可以明显看出, 本文提出的改进UKF算法对RSSI值的滤波性能良好, 滤波估计值可以非常好地跟踪真实值; 而均方误差的结果也显示, 改进后的UKF算法, 其整体性能要优于标准UKF算法, 滤波精度明显提升。

3.2 定位算法性能比较

本文模拟建立了一个移动目标室内定位系统, 系统由一个无线网卡和9个路由器组成, 9个路由器按照3× 3矩阵形式排列, 实验空间设置为20 m× 5 m(长× 宽), 面积约为100 m²。

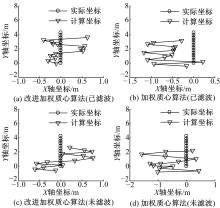
在实验过程中, 分别利用传统加权质心定位算法和改进加权质心定位算法, 在RSSI未滤波和已滤波的情况下, 对移动目标进行跟踪定位, 结果如图3所示。

	Figure Option View Download New Window
	图3 算法定位结果Fig.3 Localization algorithm results

从图3的定位结果可得到如下结论:

(1)RSSI对于定位结果有较大影响。对RSSI进行滤波以后的定位结果要明显好于未滤波的情况, 而且滤波以后的坐标分布较为集中, 说明结果稳定性更好。

(2)改进的加权质心算法的定位精度要明显高于传统加权质心算法。算法计算得到的坐标与实际坐标之间更为接近, 在上一次定位结果出现较大偏差以后, 明显有修正趋势, 说明本文算法利用定位误差对距离进行修正, 进而提高定位精度的策略是正确而有效的。

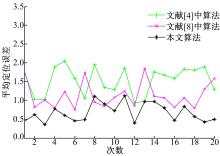
在同样的实验条件下, 与文献[4]和文献[8]中算法的定位结果进行了比较, 主要考查平均定位误差这个指标, 结果如图4所示。

	Figure Option View Download New Window
	图4 平均定位误差结果比较Fig.4 Result comparison of average error of location map

由图4的结果可知, 本文算法的平均定位误差最小, 仅为0.67 m, 文献[8]和文献[4]的定位精度要明显低于本文算法, 平均定位误差分别为1.13 m和1.52 m。这主要是因为本文算法对传统加权质心算法进行了有效改进, 利用定位偏差合理修正了RSSI距离, 并且利用改进UKF算法对RSSI值进行了滤波。而文献[4]中算法的实质就是传统加权质心定位算法, 只不过换了一种形式; 文献[8]中算法虽然对传统加权质心算法进行了一定的改进, 但是权值分配主要考虑了两个锚节点对于未知节点的影响; 而且这两种算法都未考虑RSSI的滤波问题, 故定位精度不高。

4 结束语

针对传统基于RSSI的质心定位算法静态分配权重的缺点, 提出利用定位误差对基于RSSI的距离进行修正, 从而降低定位误差, 有效提高了定位精度。对于硬件本身和环境因素引起的RSSI不稳定、带有噪声的问题, 提出了一种改进的UKF滤波算法, 采用改进的最小偏度采样策略, 有效降低了标准UKF算法的计算量, 提高了实时性, 同时采用衰减记忆滤波方法, 有效降低了测量值对于估计值的影响, 实现对于滤波发散的有效抑制。仿真实验表明, 本文提出的基于RSSI的改进加权质心算法的定位精度明显提高, 而改进的UKF滤波算法的稳定性和滤波精度也大大优于标准UKF算法。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	张锐恒, 庄毅, 赵振宇, 等. 基于MCB的传感网移动目标定位算法[J]. 计算机科学, 2012, 39(8): 34-37. Zhang Rui-heng, Zhuang Yi, Zhao Zhen-yu, et al. Mobile object localization algorithm for sensor networks based on MCB[J]. Comput Science, 2012, 39(8): 34-37. [本文引用:1]
[2]	郭力, 昂海松, 郑祥明. 基于单目视觉的微型飞行器移动目标定位方法[J]. 系统工程与电子技术, 2012, 34(5): 996-1000. Guo Li, Ang Hai-song, Zheng Xiang-ming. Moving target geolocation for micro air vehicles based on monocular vision[J]. Systems Engineering and Electronics, 2012, 34(5): 996-1000. [本文引用:1]
[3]	张云洲, 付文艳, 项姝. 室内环境下基于IMM-EKF算法的移动目标定位[J]. 计算机研究与发展, 2014, 51(11): 2408-2415. Zhang Yun-zhou, Fu Wen-yan, Xiang Shu, et al. IMM-EKF algorithm-based indoor moving target localization[J]. Journal of Computer Research and Development, 2014, 51(11): 2408-2415. [本文引用:1]
[4]	何艳丽. 无线传感器网络质心定位算法研究[J]. 计算机仿真, 2011, 28(5): 163-166. He Yan-li. Research on centroid localization algorithm for wireless sensor networks based RSSI[J]. Computer Simulation, 2011, 28(5): 163-166. [本文引用:1]
[5]	吴曦德, 方杰, 杨世杰. 基于GPSO-DVHop的传感器节点定位方法[J]. 计算机工程与应用, 2013, 49(22): 95-99. Wu Xi-de, Fang Jie, Yang Shi-jie. Wireless sensor network localization based on GPSO-DVHop algorithm[J]. Computer Engineering and Applications, 2013, 49(22): 95-99. [本文引用:1]
[6]	葛文涛, 陈俊杰. 基于三边定位的WSN锚节点加权补偿算法[J]. 测控技术, 2010, 29(9): 92-95. Ge Wen-tao, Chen Jun-jie. Weighted compensated algorithm of WSN anchor node based on trilateration localization[J]. Measurement and Control Technology, 2010, 29(9): 92-95. [本文引用:1]
[7]	王君, 高晓光. 多雷达站组合三角定位算法研究[J]. 系统工程与电子技术, 2008, 30(11): 2216-2219. Wang Jun, Gao Xiao-guang. Study on triangular locating algorithm for muli-radar station combination[J]. Systems Engineering and Electronics, 2008, 30(11): 2216-2219. [本文引用:1]
[8]	刘运杰, 金明录, 崔承毅. 基于RSSI的无线传感器网络修正加权质心定位算法[J]. 传感技术学报, 2010, 23(5): 717-721. Liu Yun-jie, Jin Ming-lu, Cui Cheng-yi. Modified weighted centroid localization algorithm based on RSSI for WSN[J]. Chinese Journal of Sensors and Actuators, 2010, 23(5): 717-721. [本文引用:1]

2012

0.0

. 2012, 39(8):34-37 DOI:doi:10.3969/j.issn.1002-137X.2012.08.007

Mobile object localization algorithm for sensor networks based on MCB

基于MCB的传感网移动目标定位算法

Zhang Rui-heng , Zhuang Yi , Zhao Zhen-yu

张锐恒, 庄毅, 赵振宇

摘　要：针对MCB移动定位算法在实时信息采样方面的不足,提出了EMCB（Enhanced Monte-Carlo localizationBoxed）定位算法。该算法在MCB算法基础之上,引入遗传算法中的变异和交叉操作,使样本选择向后验密度值较大的区域转移,从而有效地解决了原算法存在的成功采样率较低的问题。仿真实验结果表明,同MCB算法相比,EMCB算法平均采样数减少了约30%,定位精度提高了约17%。

... 受现场环境等因素的制约,定位精度常常无法满足要求,在硬件设备无法提升定位精度的情况下,只能寻求更为先进的定位算法^[1,2,3] ...

2012

0.0

. 2012, 34(5):996-1000 DOI:doi:10.3969/j.issn.1001-506X.2012.05.25

Moving target geolocation for micro air vehicles based on monocular vision

基于单目视觉的微型飞行器移动目标定位方法

Guo Li , Ang Hai-song , Zheng Xiang-ming.

郭力, 昂海松, 郑祥明

Aiming at the movement of the targets in unknown altitude terrain, a monocular camera based target geolocation method for micro air vehicles (MAV) is presented. Firstly, the optical flow histgram algorithm extracts background features in the target’s local region. Secondly, these features are clustered into two possible classes including aided plane features and non-aided plane features by the expectation maximization algorithm, in which the homography relationship between MAV ’s flight status measured by onboard micro electro mechanical systems (MEMS)/ global positioning system (GPS) sensors and planar is used. Meanwile, the normal vector of aided plane and the distance between the camera and the plane are estimated. Then the aided plane equation can be establised. Finally, the moving taregt can be geolocated by calculating the intersection of target’s sight line and aided plane in inertial frame. Experimental results show that this method can instantaneously geolocate the moving target by operator’s single click and the error can reach less than 15 m for an MAV flying at 100 m above the ground.

针对目标在地形高度未知环境中移动的情况，给出一种利用微型飞行器机载单目摄像机进行目标定位的方法。首先,借助光流直方图从当前图像帧中提取出移动目标局部区域内的背景特征点|然后,结合机载微机电系统(micro electro mechanical system, MEMS)/ 全球定位系统(global positioning system, GPS)传感器测量的飞行器位姿和空间平面点成像的单应变换关系，在期望值最大化算法中将背景特征点分类为辅助平面点和非辅助平面点，并估计辅助平面到摄像机光心的距离参数和法矢量参数，从而确定移动目标所处辅助平面的空间平面方程|最后,联立求解目标视线方程和辅助平面方程获得交点坐标，转换到惯性系下完成移动目标的地理定位。实验结果表明，当微型飞行器飞行高度为100 m时，操作人员单次点击移动目标的定位误差在15 m以内。

... 受现场环境等因素的制约,定位精度常常无法满足要求,在硬件设备无法提升定位精度的情况下,只能寻求更为先进的定位算法^[1,2,3] ...

2014

0.0

. 2014, 51(11):2408-2415 DOI:doi:10.7544/issn1000-1239.2014.20131073

IMM-EKF algorithm-based indoor moving target localization

室内环境下基于IMM-EKF算法的移动目标定位

Zhang Yun-zhou , Fu Wen-yan , Xiang Shu

张云洲, 付文艳, 项姝

It is a challenging task to improve the accuracy of the mobile localization in LOS (line-of-sight) and NLOS (non-line-of-sight) mixed environment. When the MN (moving node) moves in indoor environment, due to the obstacles such as walls, doors, and furniture, the communicating signal between MN and ANs(anchor nodes) change between LOS and NLOS frequently and randomly, which has negative effect on the accuracy of MN location estimation. To guarantee the accuracy, a KF (Kalman filter) based IMM (interacting multiple model) is proposed to filter the measured distance under the LOS/NLOS mixed environment. Due to the different characteristic of ranging errors between LOS and NLOS, two parallel KFs with different parameters are employed in order to suit for LOS mode and NLOS mode, both of the mode probabilities are calculated by the mode likelihoods and history probabilities. The modes transition between LOS/NLOS modes is based on Markov chain and mode probabilities. The weighted mean of the two modes filtering results is taken as the estimated distance of IMM. Once the estimated distances are obtained, the EKF (extended Kalman filter) is applied to locate the MN. The simulation results demonstrate the IMM can significantly mitigate the positive range error and achieve high localization accuracy.

如何在视距(line-of-sight, LOS)与非视距(non-line-of-sight, NLOS)混合的室内环境中提高移动目标定位的精度，这是一项富有挑战性的工作.移动目标在室内环境移动时，其与传感器网络节点之间的信号传播在LOS与NLOS之间随机切换，导致移动节点定位精度下降.提出一种交互式多模型-扩展卡尔曼滤波(interactive multiple model-extended Kalman filter, IMM-EKF)定位算法.根据LOS/NLOS环境下不同的测距误差特性，在IMM框架中采用2个平行的卡尔曼滤波器(Kalman filter, KF)模型对测量距离同时进行滤波，根据滤波结果和测量值计算2个模型的似然概率，模型间的转换通过Markov链实现，2个KF滤波结果加权融合后获得IMM距离估计值.在EKF定位阶段，通过位置预测和更新估计出移动目标位置.仿真结果表明，IMM-EKF算法能够有效抑制NLOS对目标定位的影响，其定位精度优于单模型算法.

... 受现场环境等因素的制约,定位精度常常无法满足要求,在硬件设备无法提升定位精度的情况下,只能寻求更为先进的定位算法^[1,2,3] ...

2011

0.0

. 2011, 28(5):163-166 DOI:doi:10.3969/j.issn.1006-9348.2011.05.040

Research on centroid localization algorithm for wireless sensor networks based RSSI

无线传感器网络质心定位算法研究

He Yan-li.

何艳丽

节点定位是无线传感器网络中的关键技术之一.质心定位算法完全依赖于锚节点的密度大小及分布情况,锚节点的密度较小且随机分布,所以质心定位算法的定位精度比较低.为了提高节点定位的精度,提出了一种改进的无线传感器网络质心定位算法.在质心定位算法中引人接收信号强度(RSSI)信息,利用RSSI计算节点间点到点的信号强度,并把信息强度值转换成距离值,取倒数作为质心算法权重值,通过质心定位算法对未知节点坐标进行计算,得到节点的具体位置.通过仿真对算法进行测试与分析,仿真结果表明,算法定位的误差减小,提高了节点定位精度,是一种有效的定位算法,为网络设计提供了依据.

... 目前的移动目标定位算法主要分为两大类:第一类是不依靠距离的定位算法,包括质心算法、凸规划算法以及DV-HOP算法等^[4,5] ...

2013

0.0

. 2013, 49(22):95-99 DOI:doi:10.3778/j.issn.1002-8331.1308-0423

Wireless sensor network localization based on GPSO-DVHop algorithm

基于GPSO-DVHop的传感器节点定位方法

Wu Xi-de , Fang Jie , Yang Shi-jie.

吴曦德, 方杰, 杨世杰

In order to reduce localization error of the wireless sensor network node, a novel localization method of the wireless sensor network node is proposed based on improved DV-Hop（GPSO-DVHop） which localization error is corrected by grouping particle swarm optimization（GPSO）. A node distance correction strategy is introduced to reduce estimation error of the distance between unknown node and anchor node, and then the node localization error of DV-Hop algorithm is corrected by GPSO algorithm. The performance of the method is analyzed on Matlab 2012. Compared with other localization methods, the proposed method has improved localization accuracy of the sensor node, and the results show the effectiveness of the proposed method.

为了减少无线传感器网络节点的定位误差，提出一种分群粒子群优化（GPSO）算法修正DV-Hop误差的传感器节点定位方法（GPSO-DVHop）。提出一种节点距离修正值策略，减少未知节点与锚节点间距离的估计误差，采用GPSO算法修正DV-Hop的节点定位误差，最后在Matlab 2012平台上对算法性能仿真分析。相对于对比传感器定位方法，GPSO-DVHop提高了传感器节点定位精度，仿真结果验证了GPSO-DVHop的有效性。

... 目前的移动目标定位算法主要分为两大类:第一类是不依靠距离的定位算法,包括质心算法、凸规划算法以及DV-HOP算法等^[4,5] ...

2010

0.0

. 2010, 29(9):92-95 DOI:doi:10.3969/j.issn.1000-8829.2010.09.025

Weighted compensated algorithm of WSN anchor node based on trilateration localization

基于三边定位的WSN锚节点加权补偿算法

Ge Wen-tao , Chen Jun-jie.

葛文涛, 陈俊杰

In order to inhibit the influence of complex environment on the location precision of nodes in wireless sensor network effectively,an anchor node weighted location algorithm was given,based on the trilateration location algorithm.The algorithm uses the anchor node’s own positioning capabilities,and obtains the positioning error in the vicinity positioning system of the anchor nodes through the weighted centroid location algorithm to compensate for the errors,which enhance the positioning precision of blind nodes.Tests show that this algorithm is simple and effective,and can be used to many applications.

为了有效抑制复杂环境对无线传感器网络节点定位精度的影响,以三边定位算法为基础,提出了一种锚节点加权补偿定位算法.该算法利用锚节点自身的定位功能,通过加权质心方法获得定位系统在锚节点附近的区域定位误差,并对该误差进行补偿,从而提高该区域盲节点的定位精度.实验结果显示,该算法简单有效,具有普遍应用意义.

... 第二类是基于距离的定位算法,主要包括三边测量算法、三角测量算法以及极大似然估计算法等^[6,7] ...

2008

0.0

. 2008, 30(11):2216-2219 DOI:doi:10.3321/j.issn:1001-506X.2008.11.043

Study on triangular locating algorithm for muli-radar station combination

多雷达站组合三角定位算法研究

Wang Jun , Gao Xiao-guang.

王君, 高晓光

多雷达站组合三角定位中,目标在接近某组合雷达基线就会偏离另一雷达组合基线.针对这一情况,提出目标接近两雷达基线的定位方程与目标远离两雷达基线的定位方程,利用专家系统思想设计多雷达站组合三角定位算法,并给出算例.从算例中可以看出,研究的算法能够提高多雷达站组合三角定位精度,具有较大的工程实用价值.

... 第二类是基于距离的定位算法,主要包括三边测量算法、三角测量算法以及极大似然估计算法等^[6,7] ...

2010

0.0

. 2010, 23(5):717-721

Modified weighted centroid localization algorithm based on RSSI for WSN

基于RSSI的无线传感器网络修正加权质心定位算法

Liu Yun-jie , Jin Ming-lu , Cui Cheng-yi.

刘运杰, 金明录, 崔承毅

提出了一种基于接收信号指示强度(RSSI)的修正加权质心定位算法,它区别于以往的加权质心定位算法,在该算法中采用测试距离倒数之和代替距离和的倒数作为权重,同时提出了修正系数的概念,避免了信息淹没现象,提高了定位精度.仿真结果表明,本文算法定位精度较之前的加权质心定位算法有了明显提高,最高可达17.83%. Abstract： Based on Received Signal Strength Indicator(RSSI),a modified weighted centroid localization algo-rithm is presented.Different from the former method,the sum of the reciprocal of each measared distance will be taken as the weight,instead of the reciprocal of sum.We also introduce a modified coefficient,which reduces the phenomenon of information drown,and the precision of localization is improved.The simulation result shows that the modified weighted centroid localization algorithm can provide an extra maximum precision gain of 17.83%,compared with the former method.

... 基于RSSI的加权质心定位算法在多个领域中都有应用,并且取得了一定的效果^[8] ...