作者简介:蔡金良(1987-),女,博士研究生.研究方向:汽车电磁兼容.E-mail:caijl10@mails.jlu.edu.cn
为了准确地分析高空核电磁脉冲作用下车辆发动机舱内的电磁环境,考虑了散热器、发动机和变速箱等不同形状、位于舱内不同位置的不规则金属设备的影响,计算了舱内500多个观测点的电场强度,并依据自参考方法验证了计算结果的准确性。最后从场强空间分布、场强峰值出现频率和谐振特性三方面分析了舱内的电磁环境。结果表明:舱内场强峰值符合瑞利分布;散热器使主谐振频率发生偏移,发动机使关键区域场强增大;金属设备显著影响舱内场强峰值的最大值,使其提高约一倍。
To precisely analyze the electromagnetic environment in automotive engine block radiated by High Electromagnetic Pulse (HEMP), the complex metallic equipments with different shapes at different positions, such as radiator, engine and gear-box were considered. The electric fields were computed at more than 500 points in the block, and the results were verified using self-reference method. Finally, the electromagnetic environment was analyzed from views of the electric field distribution, the frequency of occurrence of peak value and the electric field resonances. The results show that the electric peak values are Rayleigh distributed. The radiator leads the shift of the resonance frequency, and the engine results in the increase in electric field in important region. Metallic equipments evidently impact on the maximum electric field peak values in the block, which is doubled.
现代汽车的机动性和安全性越来越依赖于电子电控系统, 而大部分关键电子设备及线束均安装在发动机舱内。电磁脉冲(Electromagnetic pulse, EMP)技术和武器的不断发展, 使车辆电控系统的防护面临着新挑战[1, 2]。准确分析发动机舱内电磁环境效应是确保电控系统电磁防护设计有效的前提。
由于早期实验和计算条件的限制, 在车辆电磁环境研究中往往将车辆简化为等比例缩小模型或简单的矩形腔体[3, 4]。近些年数值计算和计算机技术的发展为精细建模和电磁环境效应计算提供了条件。目前已有学者按照车辆外壳实际尺寸建模并计算车内的场强[5], 在此基础上Ferrieres等[6]解决了车辆外壳曲面建模问题。Chahine等[7]则进一步建立了车架模型。由于车辆发动机舱内有发动机、变速箱、散热器等形状复杂的金属设备, 且发动机舱一般为半开放结构, 这为舱内电磁环境效应计算和分析带来困难。Siah等[8]主要在较高频段分析了发动机舱壳体及缝隙的作用, 分别计算了700 MHz和1.1 GHz电磁波照射下舱内屏蔽效能的分布。Tapigure等[9]考虑了多个金属设备的作用, 在200 MHz范围内分析了发动机舱内4个电子设备所在位置的谐振特性。上述文献均未系统分析发动机舱内复杂金属设备对电磁环境效应的影响, 因此考虑舱内复杂金属设备对电磁环境效应的影响, 对提高电磁环境效应计算精度具有重要意义。
本文以某一实际车辆为计算和分析对象, 考虑发动机、散热器和变速箱等复杂金属设备的影响, 实现了高空核电磁脉冲(High altitude electromagnetic pulse, HEMP)作用下发动机舱内电磁环境效应计算。应用IEEE Std 1597.1标准[10]验证了结果的准确性, 并通过对比舱内有无金属设备等多个情况下的电磁环境效应, 分析了不同位置和不同形状金属设备的影响效果, 为车辆电磁防护设计提供参考。
以美军标MIL-STD 464C[2]中定义的HEMP为激励源。HEMP是峰值场强为50 kV/m的平面波, 能量主要集中在500 MHz以下的频率范围内, 具体数学模型为:
式中:k=1.3; E0=50 kV/m; α =4× 107 s-1; β =6× 108 s-1。
以某车辆实际尺寸为基础, 在基于传输线矩阵算法[11]的CST2013 MS[12]计算平台上建立了车辆外壳和金属设备模型。
在频率为100 kHz~500 MHz时, 车辆壳体厚度远远超过了金属集肤深度, 同时车身缝隙可忽略[5], 故采用没有厚度的完全导体面建立外壳模型。进一步参考文献[5-7]中的建模方法, 建立了如图1(a)所示的车辆外壳模型, 图中
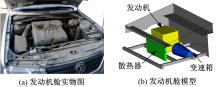
实际的车辆发动机舱及其内部结构如图2(a)所示, 从图中可以看出:发动机舱内设备非常多, 而且舱内空间有限, 同时并非舱内设备均为金属材质的。本文重点研究散热器、发动机和变速箱等位置关键且体积较大的典型金属设备的影响。
散热器、发动机和变速箱的实际结构复杂, 如图3~图5所示。若按照设备实际尺寸建模会使计算量激增, 甚至会导致无法计算。为保证计算结果准确、同时降低计算量, 参考文献[10]中的建模方法不改变金属设备的位置和体积, 采用规则的金属实体来模拟各个设备, 建立整车模型, 如图1(b)所示。散热器、发动机和变速箱在车辆模型中的具体位置如图2(b)所示。其中散热器为70 cm× 4 cm× 37 cm的矩形块, 位于发动机舱的正前方, 与舱盖相连; 发动机为45 cm× 45 cm× 12 cm和35 cm× 45 cm× 25 cm两个矩形块的组合体, 位于舱内部、顶端靠近舱盖; 变速箱为长50 cm的锥形柱(两个底面的直径分别为16 cm和25 cm), 位于舱底部。
在发动机舱内沿
最后, 对模型进行离散化即网格剖分, 同时设定计算空间, 但网格和计算空间的尺寸是在后文中确定的。
为确保计算结果准确, 用IEEE Std 1597.1标准中的自参考方法从网格、计算空间和时间长度3个方面对计算结果进行了验证, 验证流程图如图7所示(所有条件必须逐一验证)。建立初始模型后, 分别减小网格尺寸、增大计算空间、增大时间长度, 建立修改模型, 对比两模型的计算结果。若计算结果不相同则继续调整条件; 若计算结果趋于稳定不变, 认为计算模型与计算结果的准确性已满足标准要求。
以时间长度条件验证为例给出自参考验证过程。具体仿真条件为:以图1(b)整车模型为计算对象; 垂直极化HEMP平面波从正面照射车辆; 计算频率为100 kHz~500 MHz; 底面边界条件为电壁(模拟大地), 另5个面均为吸收边界; 以图1(a)中的A点为观测点; 时间长度分别取100~600 ns(以100 ns为步长)。计算结果如图8所示, 可以看出时间长度为500~600 ns时, 结果趋于稳定, 故500 ns即满足标准要求。经对网格和计算空间等另外两个条件验证后得出确保计算结果准确的条件:车模型的最小网格为0.15 cm(网格总数约为6× 108), 计算空间为8 m× 4.7 m× 3 m, 时间长度为500 ns。
实验条件:以同时考虑散热器、发动机和变速箱的整车模型为计算对象; 垂直极化HEMP平面波从正面照射车辆; 底面边界条件为电壁, 另5个面均为吸收边界; 计算频率为100 kHz~500 MHz; 时间长度为500 ns; 计算舱内517个观测点及A观测点的电场强度。
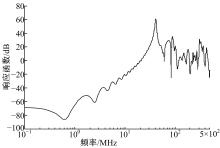
A观测点的时域场强、频域场强和响应函数分别如图10、图11和图12所示。响应函数为 H(f)=20log(EO/Ei),其中Ei为输入场强,EO 为A点场强。A点的时域峰值场强高达89kv/m, 而且频域中仅在41 MHz发生强烈谐振。从图12中可以看出, A点响应函数的整体趋势是随着频率的增大而增强, 10~500 MHz时A点的响应能力超过-20 dB, 特别是在41 MHz时, 输出场强甚至超过输入场强60 dB。
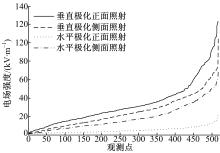
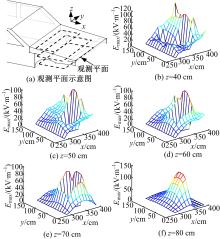
进一步分析517个观测点的时域场强峰值, 得到了峰值空间分布和出现频率分布。图13为发动机舱内不同高度观测平面上的场强峰值分布图(金属内的场强定义为0)。观测平面如图13(a)所示, 观测平面高度分别为z=40 cm、z=50 cm、z=60 cm、z=70 cm、z=80 cm。
发动机舱内场强峰值分布在0~130 kV/m时, 每个观测平面上场强分布的规律很相近。发动机附近场强比较大, 随着高度的增加, 发动机周围的场强更加突出。从图13(b)~13(e)可以看出, 每个观测平面上都是A观测点附近区域的场强最大, 而该区域内有大量车辆线束, 对车辆安全造成潜在威胁。
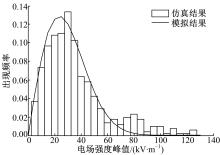
在车辆电磁环境统计分析方面, Ruddle[12]通过分析驾驶舱内大量观测点上场强值的出现频率, 得出驾驶舱内的场强值符合六自由度卡分布。故本文采用相同方法分析了发动机舱内517个观测点的场强峰值。经统计分析得到舱内场强峰值的均值为33.2 kV/m、标准差为23.5 kV/m, 出现频率如图14所示。经拟合发现峰值符合瑞利分布, 概率密度函数为:
式中:
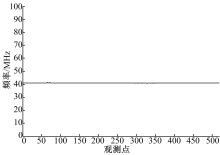
图15为发动机舱内所有观测点的谐振频率, 可以看出谐振频率与位置无关, 均为41 MHz。
为讨论发动机舱内金属设备对电磁环境效应的影响, 考虑发动机舱内包括不同金属设备的情况, 计算发动机舱内的电场环境。将第2部分中的计算模型称为模型1, 而建立的其他7个模型分别为:车辆外壳模型(模型2); 车辆外壳和散热器模型(模型3); 车辆外壳和发动机模型(模型4); 车辆外壳和变速箱模型(模型5); 车辆外壳和发动机、变速箱模型(模型6); 车辆外壳和散热器、变速箱模型(模型7); 车辆外壳和散热器、发动机模型(模型8)。
采用模型1的条件对模型2~模型8进行计算, 得到各个情况下发动机舱内517个观测点的场强。
首先对比分析有无金属设备时发动机舱内的场强峰值出现频率分布, 如图16所示。可以看出不考虑金属设备时, 舱内电场峰值的出现频率呈现为多峰分布, 由此可见金属设备确实会对发动机舱内场环境产生影响。
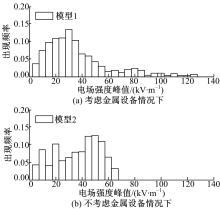 | 图16 有无金属设备时舱内场强峰值出现频率图Fig.16 Frequency of occurrence of peak value in engine block with and without three metallic equipments |
为了分析舱内金属设备对场强峰值统计特性的影响, 对模型1~模型8的计算结果进行统计分析, 得到了均值、标准差、最大值和最小值等相关统计参数, 如表1所示。在考虑不同形状和不同位置上的金属设备以及不考虑金属设备等8种情况下, 得到的场强峰值的均值几乎相同, 均为30 kV/m左右。但与不考虑舱内金属设备情况(模型2)相比, 散热器和发动机使舱内场强峰值的离散程度增大, 并显著地影响舱内场强峰的最大值, 使其增大约一倍。所以, 考虑发动机舱内的金属设备可提高关键位置处场强峰值计算的准确度, 这对关键位置处的电磁防护设计非常重要。
| 表1 统计参量对比表 Table 1 Comparison of statistical parameters kV/m |
通过做差的方式可以更直观地观察出每个金属设备对场强峰值的影响。将模型3~模型5的场强峰值与模型2的场强峰值做差, 将模型6~模型8的场强峰值与模型1的场强峰值做差, 分别如图17(a)和(b)所示。为了便于观察,
文中将差值按从小到大排列。可明显看出变速箱对发动机舱内的场强几乎没有影响, 而散热器和发动机均会导致舱内一些位置的场强增大、另一些位置的场强减小。从使舱内场强峰值增大的程度以及影响的观测点数来看, 3个金属设备中发动机的影响最大、散热器次之。结合图13中的场强峰值空间分布, 可以看出发动机的存在直接导致舱内线缆集中位置即观测点
表2中对比了模型1~模型8的主谐振频率。可以发现, 只考虑散热器时(模型1、模型3、模型7和模型8), 舱内谐振频率均为41 MHz; 而未考虑散热器时(模型2、模型4、模型5和模型6), 谐振频率均为47 MHz。这说明散热器使舱内主谐振频率发生了6 MHz偏移。
| 表2 谐振频率对比表 Table 2 Comparison of resonance frequencies |
从电磁波传播和腔体谐振原理上分析, 散热器对舱内谐振频率的影响是由它的位置和面积决定的。由于散热器位于发动机舱的正前方, 与舱盖相连接, 而且散热器的面积为0.259 m2、发动机舱正面开口面积为0.63 m2, 散热器的存在将发动机舱的正面开口面积减小了40%, 因此散热器对车辆发动机舱的谐振频率产生了较大影响。
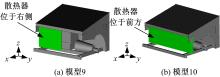
为了说明散热器位置和面积的影响, 分别在模型1的基础上改变散热器的位置和面积, 建立图18所示模型9和模型10并进行仿真分析。模型9中将散热器置于右侧, 面积仍为0.259 m2; 模型10中仍将散热器置于正前方, 但将其宽度增加至1.5 m, 使其面积与发动机舱开口面积相同。采用与模型1相同的条件对模型9和模型10进行计算, 计算结果如表3所示。在表3中还对比列出了模型1和模型2的结果。表3中的谐振频率变化证明了金属设备的位置和面积会直接影响发动机舱的谐振频率, 而且发动机舱正面开口越小舱内的谐振频率越高。
| 表3 不同散热器对应的舱内谐振频率 Table 3 Resonance frequencies of engine blocks with different radiator |
本文在同时考虑散热器、发动机和变速箱等复杂金属设备时, 计算了HEMP作用下车辆发动机舱内517个观测点的电场强度, 并依据标准验证了结果的准确性, 最后对比讨论了不同位置、不同形状的金属设备对舱内场强的影响, 为车辆电磁防护设计提供了数据支撑, 具有工程应用价值。通过对结果后处理和统计, 分析发现发动机舱内场强峰值服从瑞利分布、场强最大的区域为发动机和散热器及变速箱包围的区域(本文中
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|