作者简介:张兰(1989-),女,博士研究生.研究方向:汽车智能化检测与轨道车辆.E-mail:zhanglan_jldxjtxy@163.com
建立了基于多体动力学理论的位姿反解模型,利用Matlab/Simulink求解得到驱动试验台作动器运动的试验谱。建立了转向架试验台简化三维模型,以所生成的试验谱作为输入信号,通过SolidWorks Motion运动学分析,得到轨道不平顺复现值。将复现值与实测数据进行对比,验证了轨道不平顺复现试验谱生成方法的正确性。在转向架试验台上进行了试验验证,轨道不平顺三项参数的试验值与线路实测值相对误差均在5%以内,可以实车应用。
The reproduction of track irregularity on test bench is important, and the premise of reproducing track irregularity is the generation of the test spectrum to drive the test bench. Based on the multi-body dynamics theory, an inverse kinematics solution model is established, and the test spectrum of the actuators to drive the test bench is obtained by Matlab/Simulink simulation. A simplified 3D model of the bogie test bench is established, and the generated test spectrum is taken as the input signal. Then, the reproductive value of the track irregularity is obtained by kinematics analysis using SolidWorks Motion. The comparison of the reproductive value with the measured data verifies the validity of the proposed generating method of the test spectrum for track irregularity reproduction. Verification experiments are carried out on the bogie test bench, and results show that the relative errors of the three parameters of track irregularity between test value and measured data are within 5%, which proves the test spectrum used for track irregularity reproduction can be applied to real vehicle experiment.
轨道不平顺是轨道-车辆系统的激扰源, 是引起车辆产生振动和轮轨作用力的主要原因, 对列车运行的安全性、稳定性和舒适性具有重要影响[1, 2]。在试验台上复现轨道不平顺可以模拟实际线路运行状况, 使转向架及整车的各项性能测试试验更加接近真实值。通过试验台复现轨道不平顺进行相关试验, 需输入特定的激励信号作为激扰函数[3, 4]。实测轨道不平顺数据需要经过分析处理转换为驱动试验台运动的试验谱。日本铁道综合技术研究所研发的车辆试验台能用现车模拟实际轨道的状态, 但不能充分地预测在干线钢轨上运行车辆的响应特性。针对此项不足, 足立雅和等[5]采用新的激振系统, 引入加权函数修正枕木方向的不平整, 开发了在试验台上评价干线车辆响应特性的系统。西南交通大学的滚动振动试验台用轴箱的位移信号模拟轨道不平顺, 并将此信号作为目标信号, 通过迭代算法生成试验所需试验谱[6]。但是, 引入加权函数修正法和迭代法计算过程复杂, 且精度不高。吉林大学研发的转向架试验台, 可以准确地复现轨道不平顺, 通过旋转矩阵变换, 直接计算得到驱动平台运动的作动器的位移, 不需要迭代计算, 计算过程简单且准确。
本文建立了生成轨道不平顺复现试验谱的位姿反解模型, 利用Matlab/Simulink对某线路实测轨道不平顺数据进行仿真求解, 得到驱动转向架试验台作动器运动的试验谱。将试验谱输入到建立的转向架试验台简化三维模型中, 通过SolidWorks Motion运动学分析得到轨道不平顺复现值。将复现值与实测数据进行对比, 验证生成轨道不平顺复现试验谱方法的正确性。将生成的试验谱作为激励信号输入到转向架试验台中进行试验验证, 分析误差, 证明本文生成的轨道不平顺复现试验谱可以运用到实车试验中。
转向架试验台作为一种多功能试验设备, 可以通过复现轨道不平顺实现对转向架装配条件下和整车落成状态下的实际线路运行工况的模拟。
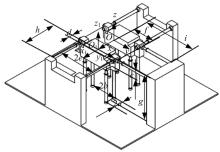
图1为转向架试验台模型图, 转向架试验台包括两个独立的六自由度运动平台, 分别对转向架的两个轮对进行激励, 每个运动平台包括4个垂向作动器(图中编号为1~4)、2个纵向作动器(图中编号为5、6)和1个横向作动器(图中编号为7)共7个作动器, 对7个作动器输入位移试验谱可以在转向架试验台上复现轨道的水平不平顺、方向不平顺和高低不平顺。
转向架试验台实车试验前, 需要进行模拟仿真, 验证所生成试验谱的正确性, 以确保轨道不平顺复现试验的准确可靠。图2为按照1:1的比例建立的转向架试验台的简化三维模型, 用于在虚拟环境下模拟转向架试验台轨道谱的复现。试验台的结构参数如表1所示。
| 表1 试验台结构参数 Table 1 Geometric parameters of the test bench |
轨道不平顺反映的是轨道实际状况, 对于同一线路, 转向架前轴和后轴所受的轨道激励相同, 只是存在延时, 因此只需对其中一个运动平台进行运动学分析, 求解7个作动器的位移。
以1#运动平台为例, 创建如图2所示的全局坐标系O-xyz, 选取两个运动平台的横向和纵向对称面的交线在轨道平面内的投影点作为全局坐标系的原点O, 车辆行驶方向为x轴, 垂直于轨面方向为z轴, 根据右手法则确立y轴。建立1#运动平台的局部坐标系O1-x1y1z1, 选取1#运动平台两纵向作动器的纵向中心线的对称线与横向作动器的横向中心线的交点为局部坐标系坐标原点O1, x1、y1、z1的方向与全局坐标系x、y、z的方向相同。1#运动平台局部坐标相对于全局坐标的位姿可用广义坐标P=(α , β , γ , x0, y0, z0)描述, α 、β 、γ 为局部坐标系相对于全局坐标系的三个绕x、y、z轴的旋转量, x0、y0、z0为局部坐标系相对于全局坐标系沿x、y、z三个坐标轴的平移量[7, 8]。
1#~7#作动器上铰链点A和下铰链点B在局部坐标系中的坐标表示为:
轨道水平不平顺、方向不平顺、高低不平顺转化为1#运动平台的运动分别为绕x轴的转动、沿y和z轴的平动, 相应的齐次坐标变换矩阵为:
因此, 1#~7#作动器的伸缩量表示为:
式中:
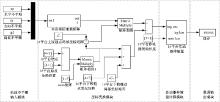
基于上述理论, 利用Matlab/Simulink搭建轨道不平顺位姿反解仿真模型, 求解7个作动器的位移, 模型如图3所示。
轨道不平顺位姿反解仿真模型包括轨道不平顺输入模块、坐标变换模块、作动器伸缩量计算模块和数据输出模块。轨道不平顺输入模块将轨道水平不平顺、方向不平顺和高低不平顺数据导入模型中, 作为坐标变换模块的输入函数。坐标变换模块包括齐次坐标变换矩阵模块和1#平台上下铰链点坐标矩阵调整模块, 1#平台上铰链点坐标矩阵根据1#平台的原点在全局坐标系中的位置以及1#平台绕点坐标进行调整, 调整后的坐标矩阵与齐次坐标变换矩阵相乘, 1#平台下铰链点坐标矩阵根据1#平台的原点在全局坐标系中的位置、1#平台绕点坐标以及装配完成后作动器在初始位置坐标变化值进行调整。将变换后的上铰链点坐标矩阵减去下铰链点坐标矩阵即可得到位姿变换后的作动器杆长矩阵, 将杆长矩阵与作动器初始长度矩阵输入到作动器伸缩量计算模块中, 求解作动器伸缩量, 最后输出数据。
轨道不平顺输入模块输入的是轨道水平不平顺、方向不平顺和高低不平顺, 因此需要将实测数据处理后输入到模型中。轨道水平不平顺、方向不平顺和高低不平顺是通过左、右钢轨的横向和垂向位移确定。轨道水平不平顺是指左、右钢轨对应点的高度差所形成的沿轨长方向的不平顺[9], 用θ 表示为:
轨道方向不平顺是指左右两根钢轨沿长度方向在横向平面内呈现的弯曲不直, 用y表示为:
轨道高低平顺是指钢轨表面在同一轮载作用下所形成的沿长度方向的高低不平。用z表示为:
式中:yl为左钢轨的横向位移; yr为右钢轨的横向位移; zl为左钢轨的垂向位移; zr为右钢轨的垂向位移; l0为左右两轨接触点距离。
通过Matlab编写M文件, 导入左、右钢轨的横向、垂向位移(yl、yr、zl、zr), 求出轨道水平不平顺、方向不平顺和高低不平顺实测数据。坐标变换模块和作动器伸缩量计算模块中所需参数均用同一个M文件编写, 在Simulink仿真分析前, 先运行此M文件。仿真分析结束后, 得到7个作动器实时位移解算结果。
将转向架试验台三维模型导入到SolidWorks Motion中进行运动学分析, 创建运动算例, 分别对7个作动器添加7个线性马达, 每个线性马达输入数据为轨道不平顺位姿反解仿真模型中得到的对应作动器的位移数据, 分析时间和采样频率与Matlab/Simulink模型中一致。计算运动算例, 输出轨道水平不平顺、方向不平顺和高低不平顺, 即轨道不平顺的复现值。
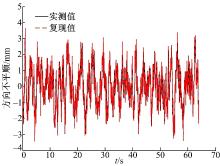
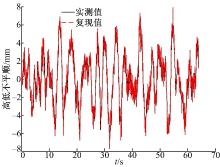
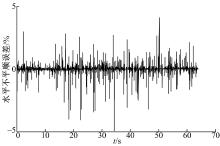
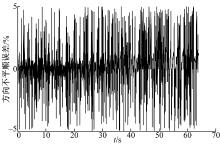
将轨道不平顺的复现值与线路实测值进行对比, 图4、图5、图6分别为水平不平顺、方向不平顺和高低不平顺的复现值与实测值的对比图。经分析, 水平不平顺、方向不平顺和高低不平顺的复现值与实测值的相对误差为0, 验证了本文所述轨道不平顺复现试验谱生成方法的正确性, 可以将此位移试验谱作为激励信号输入到转向架试验台对应的作动器中, 在试验台上复现轨道谱。
在确定了1#运动平台7个作动器的位移试验谱后, 2#运动平台7个作动器的位移可由1#运动平台试验谱结合延时时间参数Δ t计算得到, 其中:
式中:l为轴距; v为车速。
1#运动平台激励为:
2#运动平台激励为:
将所生成的位移试验谱作为激励信号输入到转向架试验台对应的14个作动器中, 得到轨道不平顺的试验值。多次重复试验, 比较试验结果。图7、图8、图9分别为水平不平顺、方向不平顺和高低不平顺的试验值与线路实测值的误差对比图。轨道不平顺三项参数的相对误差均在5%以内, 可见, 转向架试验台对轨道不平顺的复现是可行的并且复现精度较高。误差产生的主要原因是试验台作动器精度低于实测值、试验台存在装配误差以及数据采集系统存在误差等。试验证明了本文生成的轨道不平顺复现试验谱可以运用到实车试验中。
(1)提出了基于多体动力学理论的转向架试验台轨道不平顺复现试验的驱动试验谱生成方法, 建立了位姿反解模型, 并利用Matlab/Simulink模块对某线路实测轨道不平顺数据进行仿真求解, 得到了驱动转向架试验台作动器运动的位移试验谱。
(2)建立了1:1的转向架试验台简化三维模型, 以所生成的试验谱作为输入位移信号, 通过SolidWorks Motion运动学分析, 得到轨道不平顺复现值。
(3)将轨道不平顺的复现值与实测数据进行对比, 相对误差为0, 验证了本文所述轨道不平顺复现试验的驱动试验谱生成方法的正确性。
(4)将本文所生成的14个作动器位移试验谱作为激励信号输入到转向架试验台中进行轨道不平顺复现试验, 轨道不平顺三项参数的试验值与线路实测值相对误差均在5%以内, 证明转向架试验台对轨道不平顺的复现是可行的并且复现精度较高。因此, 本文生成的轨道不平顺复现试验谱可以运用到实车试验中。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|