作者简介:隗海林(1969-),男,教授,博士生导师.研究方向:车辆节能技术.E-mail:khl69@163.com
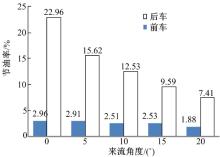
车辆进行尾随行驶时其外流场会受到侧向风及车间距变化的影响,为此本文参照沃尔沃某型号货车,按照1:1的比例建立了货车仿真模型,利用XFlow作为数值仿真软件,分别对车间距离变化范围为0~30 m及侧风来流角度变化范围为0°~20°的情况进行了数值仿真,并从汽车风阻系数变化及节油效果两个方面进行了具体分析。结果显示,在没有侧向风时后车平均节油率为22.96%,当侧向风来流角度为20°时,后车的平均节油率仅为7.41%,表明侧向风的存在大大降低了货车尾随行驶的节油效果。
The external flow-field around trucks would be affected by the lateral wind and their longitudinal spacing change when the trucks travel in tandem. In order to analyze the influence, in reference to the Volvo truck, a simulation truck model with scale of 1: 1 was established. XFlow software was used as the numerical simulation tool. The longitudinal spacing ranged from 0 m to 30 m, and yaw angle of the wind variation range was 0 to 20 degree. The simulation results were analyzed from two aspects, drag coefficient change and fuel-saving rate. The results show that the average fuel-saving rate of the following truck is about 22.96% without lateral wind. While at yaw angle of 20 degree of the lateral wind, the fuel-saving rate is only about 7.41%. This suggests that the lateral wind has great influence on the fuel-saving of the trucks traveling in tandem.
随着中国经济的快速发展, 公路货运量、公路货运周转量正在持续增长, 载货汽车的保有量也在不断增加[1]。与轿车等小型汽车相比, 载货汽车发动机排量高, 车身迎风面积大, 且车辆常处于高负荷、低速度下行驶, 所以在行驶过程中具有耗油量大、排放性差等特点。受国际能源危机及大气污染的影响, 国家对车辆节能环保的要求越来越严格。如何提高货车的燃油经济性, 减少有害物的排放, 已成为当前研究的热点[2, 3]。相关研究表明[4, 5], 汽车列队行驶能够有效降低队列中各车油耗, 增加道路的通行能力, 提高运输的经济效益, 具有较高的应用潜力。汽车列队行驶属于智能交通系统(ITS)的范畴, 它集成了先进的数据通信技术、传感器技术、电子控制技术、计算机及人工智能等高科技技术于一体, 在保证安全的前提下使车辆在较小的间距下行驶。早在1995年德国的奔驰公司就对间距在10 m范围内变化的两车尾随行驶进行了实车实验, 实验中前车为有人驾驶, 而后车处于无人驾驶状态[6]。瑞典的斯堪尼亚公司通过在车上安装自适应巡航系统(ACC), 控制两辆相同的卡车近距离尾随行驶, 实现了4.7%~7.7%的节油效果[7]。日本新能源产业技术综合开发机构(NEDO)也采用头车有人驾驶、尾随车无人驾驶的形式, 成功实现了4辆卡车时速为80 km/h、间距为4 m的列队行驶的实验, 车队平均燃油效率提高了约15%左右[8]。
目前, 虽然针对列队行驶的研究较多, 但国内外鲜有涉及侧向风对列队行驶影响的研究报道。由于自然风普遍存在, 汽车在实际道路上行驶时受侧向风影响的情况是不可避免的。尤其当车辆以列队行驶的方式在道路上行驶时, 由于车队中各车外流场本身就存在相互作用, 所以当受到侧向风影响时, 车队整体的外流场势必会受到较大影响, 因此针对该方向的研究具有较高的现实意义。本文选用基于格子波尔兹曼方法的新一代CFD技术XFlow作为数值仿真软件, 对两车同时受侧向风和车间距变化共同影响的情况进行了仿真分析, 从两车的风阻系数及燃油节省率两方面对相应的变化规律进行了总结分析。
为了达到仿真实验的预期目标, 本文对5种不同角度的模拟来流及18种不同间距下的两车尾随行驶模型分别进行了仿真分析。其中模拟来流角度取值为0° 、5° 、10° 、15° 、20° , 两车间距取值为0、1、2、3、4、5、6、8、10、12、13、14、15、18、21、24、27、30 m。由于队列间距越小, 队列中各车气动阻力对车间距离的变化越敏感, 所以本文选取了一些仅适用于理论分析的极限车间距(如0、1 m等), 目的就是为了更好地掌握其变化规律, 为今后的相关研究提供一定的理论依据。
XFlow中在车身坐标的
根据数值模拟的示意图, 易得实际来流速度
| 表1 α 、行驶车速、侧向风速及模拟来流速度 Table 1 Magnitude of yaw angle, truck velocity, lateral wind speed and the simulated wind speed |
本文参照沃尔沃某款货车的结构外形及尺寸, 按照1:1的比例利用Solidworks建立了货车模型, 具体尺寸见表2。为了实验的顺利进行, 这里对模型进行了适当简化处理, 但保留了对风阻影响较大的一些部件, 如后视镜、油箱等, 图2为单车模型的三维视图。
| 表2 汽车模型相关尺寸 Table 2 Dimension of the truck model |
计算域的大小对数值仿真的收敛速度以及计算结果的准确性都会有较大的影响。本文选取的计算域类型为虚拟风洞, 所以在确定计算域大小之前, 首先要考虑风洞的阻塞比问题[9]。风洞阻塞比的表达式为:
图3(a)(b)分别为无侧向风影响时美国南加州大学学者在Dryden风洞中测得的两车队列的风阻系数[10]以及本次数值仿真得到的两车队列的相对风阻系数的变化情况。相对风阻系数为尾随车辆内阻系数与相应单车风阻系数的比值。
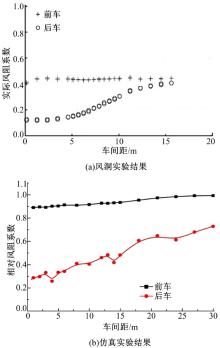 | 图3 无侧风影响时风洞实验和数值仿真 得到的风阻系数变化情况Fig.3 Drag coefficient changes trend without lateral wind by wind tunnel and numerical simulation |
对比图3(a)(b)可以看出, 数值模拟结果与风洞实验结果的整体变化趋势基本一致, 表明本次仿真实验的结果是可信的。同时可以看到, 在无侧风影响时, 前车风阻系数受两车间距变化的影响较小, 而后车风阻系数随两车间距的增加基本上呈持续增大的趋势, 这是由于前车对后车的屏障作用随两车间距的增加而逐渐减弱缘故。
图4(a)~(d)为数值模拟得到的两车尾随行驶时在不同车间距下受不同角度来流影响时车辆气动阻力系数的变化情况。
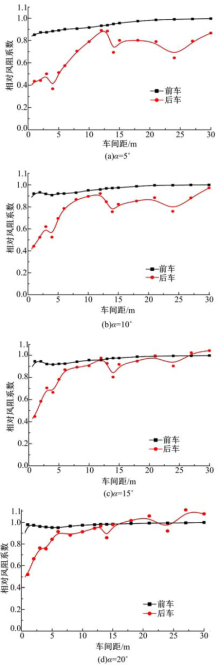 | 图4 数值仿真得到的不同来流角度影响下的相对风阻系数变化情况Fig.4 Relative drag coefficient of the trucks at different degrees yaw angle by using numerical simulation |
就前车而言, 由于前车直接承受前方来流的冲击, 所以其风阻系数始终较大。由图3(b)及图4(a)~(d)可以看出, 前车风阻系数受侧向风及车间距的影响均较小。但是, 当两车间距小于4 m时, 来流角度越大, 前车风阻系数对车间距变化的敏感度越高。对比图4(a)中前车风阻系数变化曲线与图3(b)中的曲线可以看出, 在间距小于6 m时, 前车相对风阻系数反而小于无侧风影响的情况, 但这并不代表此时前车承受的气动阻力比无侧风影响时小, 只是说明此时前车风阻系数与相同来流条件下单车风阻系数的比值较小, 即此时前车风阻系数的降低率高。由图4(b)(c)(d)可以看出, 随着来流角度的增加这种“ 优势” 会逐渐减弱, 只有进一步缩小间距才能获得较高的风阻系数降低率。特别是在来流角度为20° 的情况下, 只有当间距小于0.5 m时, 前车相对风阻系数才会比无侧风影响时低。
就后车而言, 由于后车几乎完全浸没在前车的尾流中, 因此前车尾流的变化会对后车气动特性产生较大的影响。图4(a)~(d)显示, 即便是较小角度的来流也会对后车的气动阻力产生较大影响。尤其是在车间距离大于12 m以后, 后车风阻系数的变化出现了明显的波动, 这与车队外流场中的气流脉动有关。随着
为了更直观地分析尾随行驶时车间距、侧向风对车辆风阻系数的影响, 本文对车间距离、来流角度
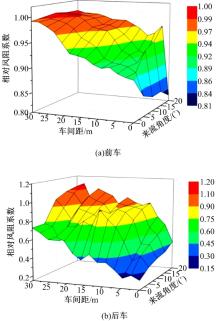 | 图5 两车间距、来流角度及相对风阻系数三维关系图Fig.5 Three dimensional diagram of longitudinal spacing yaw angle and relative drag cofficient |
从前车的三维关系图中可以看出, 在间距较小时前车对
综上, 侧向风的存在增加了两车整体的风阻系数, 并且对后车的影响程度要远大于前车。尤其是遇到大角度的侧向风, 在车距较大时将会大大增加车队的气动阻力, 这势必会使整车的燃油经济性变差。
汽车在水平良好路面上等速行驶时, 消耗的燃油基本上都用来克服滚动阻力和空气阻力[11], 所以降低汽车风阻系数对汽车的燃油经济性产生积极的影响。为了进一步分析不同侧向风及车间距对货车尾随行驶节油效果的影响, 这里对各车的节油率进行了计算。汽车在水平路面上等速行驶时, 若忽略行驶过程中气动升力的影响, 其行驶方程为:
式中:
为克服滚动阻力和空气阻力, 发动机需提供的功率为:
则百公里燃油消耗量为[11]:
式中:
定义节油率:
风阻系数降低率:
式中:
联立式(1)~(6)整理可得:
若令
由式(7)(8), 取
由式(8)可知, 汽车的节油率与其风阻系数的降低率成正比, 为了分析侧向风和车间距对尾随行驶节油率的不同影响, 这里分别以来流角度
图6中每个柱形图表示在该角度来流条件下汽车以不同间距进行尾随行驶时的平均节油率。例如, 在
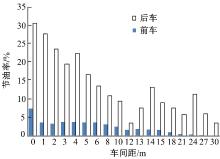
图7中每个柱形图代表该间距条件下车辆遭遇不同角度来流时的平均节油率。例如, 在取极限车间距为0 m时, 前车和后车在5种角度模拟来流影响下的平均节油率分别为7.49%和30.67%。从图中可以看出, 前车的节油率整体上是随着车间距的变大而不断降低, 在间距超过18 m以后, 前车平均节油率已不足1%。而对于后车来说, 由于受到前车屏障作用的影响, 所以其节油率受两车间距变化的影响较大。从图7还可以看到, 当两车间距为0 m时后车平均节油效果最好, 但后车平均节油率并不是随着车间距的增加而一直降低, 在4、14和24 m均有一个高点, 而在12 m处出现了一个明显凹点, 表明该位置后车气动阻力较大、节油效果差。
(1)当车队遭遇侧向风时, 两车风阻系数明显增加, 尾随行驶的节油效果有所降低。但通过适当减小两车间距, 仍可以获得可观的节油效果。
(2)前车节油效果受两车间距变化的影响较大, 受侧向风的影响较小, 而后车节油效果受两者变化的影响均较大。
(3)无侧向风影响时, 后车在各间距下的平均节油率最高可达22.96%; 当来流角度为20° 时, 后车节油率只有7.41%。
(4)在各角度来流影响下, 后车在极限间距时的平均节油率最高可达30.67%, 而间距为30 m时平均节油率仅为3.55%, 且后车节油效率与车间距没有明显的线性关系。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|