基于小型无人机摄影测量的交通事故现场勘查

引用本文

陈强, 许洪国, 谭立东. 基于小型无人机摄影测量的交通事故现场勘查. 2016, 46(5): 1439-1446
CHEN Qiang, XU Hong-guo, TAN Li-dong. Surveying method of traffic accident scene based on SUAV photogrammetry. Journal of Jilin University Engineering and Technology Edition, 2016, 46(5): 1439-1446 复制到剪切板

Permissions

基于小型无人机摄影测量的交通事故现场勘查

陈强, 许洪国, 谭立东

吉林大学交通学院,长春 130022

通信作者:许洪国(1955-),男,教授,博士生导师.研究方向:交通运输安全工程,汽车安全.E-mail:xuhg@jlu.edu.cn

作者简介:陈强(1981-),男,博士研究生.研究方向:车辆可靠性与安全技术.E-mail:qf_chenqiang@163.com

基金:“863”国家高技术研究发展计划项目(2009AA11Z201); 国家自然科学基金项目(51078167).

摘要

为了解决道路交通事故现场二维勘测中“四点法”的不足和实际应用问题,提出了基于小型无人机摄影测量的“改进四点法”。首先,通过小型无人机拍摄事故现场图像;其次,对事故现场图像采用预先对控制点信息进行归一化处理的方式减少校正过程中病态矩阵求解问题;然后,调用图像校正算法将透视图校正为正投影图;最后,以校正后的正投影图为依据,调用图像量测模块在新的正投影图上进行测量、记录和标注。通过控制场地测试和典型交通事故案例现场测试验证了该方法的有效性。与传统人工测绘以及图像测量方法相比,该方法在提高事故现场勘测精度的同时,扩展了勘测现场范围,抑制了拍摄角对“四点法”精度的影响。

关键词: 交通运输系统工程; 交通事故; 摄影测量; 改进四点法; 小型无人机

中图分类号:U491 文献标志码:A 文章编号:1671-5497(2016)05-1439-08

Surveying method of traffic accident scene based on SUAV photogrammetry

CHEN Qiang, XU Hong-guo, TAN Li-dong

College of Transportation, Jilin University, Changchun 130022, China

Abstract

In order to solve the deficiency and limit of using “4-point photogrammetric method” in 2D surveying of traffic accident scene, an improved 4-point surveying method was proposed, which was based on Small Unmanned Aircraft Vehicle (SUAV). First, the traffic accident scene images are capture by SUAV. Second, the captured images are transmitted back to the image pickup device immediately, and a pre-normalized approach for control point information processing is applied to reduce pathological situation of matrix calculation in the correction process. Then, the image correction algorithm is employed to rectify the perspective image to orthographic image. Finally, an image measuring module is used to measure, record and mark the information on the basis of the orthographic image. A control field test and an accident cased were used to validate the proposed method. Compared with the traditional manual surveying and photogrammetric method, the proposed method can not only improve the accuracy of accident scene surveying, but also expand the scope of the investigation, and constrain the impact of project angle on the accuracy of 4-point photogrammetric method.

Keyword: engineering of communication and transportation system; traffic accident; photogrammetry; improved four-point method; small unmanned aircraft vehicles(SUAV)

Show Figures

0 引言

传统的交通事故现场勘查方法, 首先采用皮卷尺测量相关距离, 然后手工绘制现场草图及现场比例图。这需要占用事故现场路段、中断交通, 容易诱发二次交通事故, 且存在费时长、现场信息遗漏多、勘测精度低, 现场量测的数据和绘制的草图因操作者存在差异, 以及恢复交通后无法对现场复查勘测等缺陷, 给事故责任判断造成很大麻烦^{[1, 2]}。在交通事故现场拍摄的照片(图像)中包含有现场大量信息, 如车辆停止位置、制动拖印、轮胎印迹、油污迹、碎片散落分布位置等^{[3, 4]}。因此, 国内外出现了大量不同形式和复杂度的采用摄影测量技术分析车辆和现场信息的研究成果, 以便快速、精确地获得交通事故现场的重要信息, 用于交通事故现场的重建。目前, 为了实现摄影图像校正测量, 出现了一些商用软件, 如PC-RECT、PhotoModeler、iWitness和123D Catch等^{[5, 6, 7, 8, 9]}。这些软件提供一系列鲁棒好的摄影图像测量分析。其中, 频繁用于交通事故现场重建的“ 平面到平面” 的二维校正算法, 是计算机视觉算法领域的重要分支^{[10, 11, 12, 13]}, 可用于一般平面现场数据的测量。二维校正算法假定图像上的点都清晰地位于空间中的同一平面上, 使用单张照片采用“ 四点法” 重建事故现场。该方法具有简单、快捷和信息易于保存等优点, 但是其勘测精度受摄影角度、摄影位置的影响较大。校正误差与摄影倾角密切相关, 倾角越小, 相同像点误差造成的实际校正误差越大。理想的拍摄角度应垂直于地面^[14], 这在采用普通相机人工拍摄方法中实际上无法达到。

近来, 小型无人机(Small unmanned aircraft vehicles, SUAV)摄影测量技术迅速发展^[15], 在大比例尺地形图测绘领域得到了广泛应用。而且, 其携带的摄像头可以满足《道路交通事故现场勘验照相》(GA50-2005)关于成像分辨率的要求。本文结合无人机摄影测量技术对“ 四点法” 进行改进, 通过无人机拍摄事故现场图像, 然后对控制点信息进行归一化处理以减少计算中的病态问题, 再将透视图校正为正投影图, 最后在校正后的正投影图上进行测量、记录和标注。通过控制场地试验测试和典型交通事故案例测试验证了该方法的有效性。

1 四点法

假定图像上的点都位于空间中的同一个平面上, 仅单张照片就可重建交通事故现场。当图像中4个任意三点不共线的参考点的像素坐标及其在空间平面上的坐标已知时, 就能够确定图像上的点和空间平面上的点的一一对应关系^[16]。

1.1 小孔模型

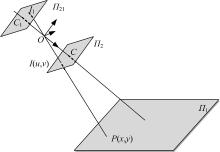
所有景物通过摄像机光轴中心点投射到成像平面上的摄像机模型, 称为小孔模型^[12]。如图1所示, $O$ 摄像机的光轴中心点, 是指摄像机镜头的光心, 为 $OC$ 为摄像机的主光轴, $Π_{1}$ 为空间平面, $Π_{21}$ 为摄像机的成像平面, $Π_{2}$ 为摄像机的数字图像平面。由小孔成像原理可证, 物体在成像平面 $Π_{21}$ 上的像是倒实像, 数字图像平面 $Π_{2}$ 上的像是正实像, 是对成像平面上的倒实像进行了放大和转换。在这3个平面上分别建立欧式坐标系, 定义空间平面上任意一点 $P$ 的坐标为 $(x, y)$ , 其在数字图像平面上的对应像点I的坐标为 $\begin{matrix} (u, v) 。 \end{matrix}$

	Figure Option View Download New Window
	图1 小孔成像原理Fig.1 Pinhole imaging

1.2 射影变换

对点 $P (x, y)$ 和 $I (u, v)$ 分别建立对应点的齐次坐标。对于 $\forall s \neq 0$ , 定义 $p = {(xs, ys, s)}^{T}$ ; 对于 $\forall t \neq 0$ , 定义 $\begin{matrix} i = {(ut, vt, t)}^{T} 。 \end{matrix}$

射影变换是射影平面上的可逆齐次线性变换, 可由3× 3的矩阵来描述:

$\begin{matrix} i = [\begin{matrix} ut \\ vt \\ t \end{matrix}] = [\begin{matrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & h_{33} \end{matrix}] [\begin{matrix} xs \\ ys \\ s \end{matrix}] = Hp (1) \end{matrix}$

式中:矩阵 $\begin{matrix} H \end{matrix}$ 为射影变换矩阵。

由于变换是齐次的, 所以同一个射影变换矩阵 $H$ 可以相差一个非零常数因子, 设 $h_{33} = 1$ , 因此射影变换仅有8个未知数, 即 $\begin{matrix} h_{11}, \dots, h_{32} \end{matrix}$ 。

1.3 算法

将式(1)的第一行、第二行分别除以第三行, 解得:

$\begin{matrix} \{\begin{matrix} u = \frac{h_{11} x + h_{12} y + h_{13}}{h_{31} x + h_{32} y + 1} \\ v = \frac{h_{21} x + h_{22} y + h_{23}}{h_{31} x + h_{32} y + 1} \end{matrix} (2) \end{matrix}$

对式(2)化简、移项, 得:

$\begin{matrix} \{\begin{matrix} u = h_{11} x + h_{12} y + h_{13} - h_{31} xu - h_{32} yu \\ v = h_{21} x + h_{22} y + h_{23} - h_{31} xv - h_{32} yv \end{matrix} (3) \end{matrix}$

求解射影变换矩阵 $H$ 的8个未知数 $h_{11}, \dots, h_{32}$ 时, 可通过4对物点 $P_{k} (x_{k}, y_{k})$ 和像点 $I_{k} (u_{k}, v_{k})$ 建立包含8个未知数的方程组 $\begin{matrix} (k = 1, 2, 3, 4) 。 \end{matrix}$

假定向量 $h = (h_{11}, h_{12}, h_{13}, h_{21}, h_{22}, h_{23}, h_{31}, h_{32})^{T}$ , 向量 $\begin{matrix} b = (u_{1}, u_{2}, u_{3}, u_{4}, v_{1}, v_{2}, v_{3}, v_{4})^{T}, \end{matrix}$ 矩阵:

$\begin{matrix} K = [\begin{matrix} x_{1} & y_{1} & 1 & 0 & 0 & 0 & - x_{1} u_{1} & - y_{1} u_{1} \\ x_{2} & y_{2} & 1 & 0 & 0 & 0 & - x_{2} u_{2} & - y_{2} u_{2} \\ x_{3} & y_{3} & 1 & 0 & 0 & 0 & - x_{3} u_{3} & - y_{3} u_{3} \\ x_{4} & y_{4} & 1 & 0 & 0 & 0 & - x_{4} u_{4} & - y_{4} u_{4} \\ 0 & 0 & 0 & x_{1} & y_{1} & 1 & - x_{1} v_{1} & - y_{1} v_{1} \\ 0 & 0 & 0 & x_{2} & y_{2} & 1 & - x_{2} v_{2} & - y_{2} v_{2} \\ 0 & 0 & 0 & x_{3} & y_{3} & 1 & - x_{3} v_{3} & - y_{3} v_{3} \\ 0 & 0 & 0 & x_{4} & y_{4} & 1 & - x_{4} v_{4} & - y_{4} v_{4} \end{matrix}], \end{matrix}$

根据式(3), 有:

$\begin{matrix} Kh = b (4) \end{matrix}$

由方程(4)对物点 $P_{k} (x_{k}, y_{k})$ 和像点 $I_{k} (u_{k}, v_{k})$ 的坐标求出向量 $b$ 和矩阵 $K$ 的值后, 通过解方程(4)可以计算出向量 $h$ 的值, 从而构造出射影变换矩阵 $\begin{matrix} H \end{matrix}$ 。

2 改进四点法

2.1 归一化处理

实际计算时, 物点 $P (x, y)$ 和像点 $I (u, v)$ 的坐标值较大, 并且单位不同, 如像素、厘米等。大的坐标值将导致矩阵 $\begin{matrix} K \end{matrix}$ 病态化, 而且不同的单位导致测量系统数据不一致, 影响图像校正精度。为了避免上述问题, 在使用方程(4)计算前, 先对物点和像点坐标值采用平移和缩放变换, 进行归一化处理^[17], 如图2所示。

	Figure Option View Download New Window
	图2 归一化处理示意图Fig.2 Schematic diagram of normalizing transformation

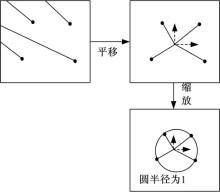
将所有点的中心作为原点, 构建坐标系, 利用式(5)把每一个点的坐标转换为在该坐标系下的坐标:

$\begin{matrix} P_{T} = [\begin{matrix} x_{T} \\ y_{T} \end{matrix}] = [\begin{matrix} x_{k} - \bar{x} \\ y_{k} - \bar{y} \end{matrix}]; I_{T} = [\begin{matrix} u_{T} \\ v_{T} \end{matrix}] = [\begin{matrix} u_{k} - \bar{u} \\ v_{k} - \bar{v} \end{matrix}] (5) \end{matrix}$

式中:

$\begin{matrix} \bar{x} \end{matrix}$ = $\begin{matrix} \frac{1}{4} \end{matrix} \begin{matrix} \overset{4}{\sum_{k = 1}} \end{matrix}$ x_k; $\begin{matrix} \bar{y} \end{matrix}$ = $\begin{matrix} \frac{1}{4} \end{matrix} \begin{matrix} \overset{4}{\sum_{k = 1}} \end{matrix}$ y_k; $\begin{matrix} \bar{u} \end{matrix}$ = $\begin{matrix} \frac{1}{4} \end{matrix} \begin{matrix} \overset{4}{\sum_{k = 1}} \end{matrix}$ u_k; $\begin{matrix} \bar{v} \end{matrix}$ = $\begin{matrix} \frac{1}{4} \end{matrix} \begin{matrix} \overset{4}{\sum_{k = 1}} \end{matrix}$ v_k。

假设像点 $I$ 的 $u$ 坐标为 ${1000.5, 1001.3, 998.7, 999.5}, v$ 坐标为 ${2001.6, 2000.7, 1998.4, 1999.3}$ , 通过设置平移量 ${\bar{u} = 1000, \bar{v} = 2000}$ , 上述坐标变为 $\begin{matrix} u {2.6, 1.4, - 1.3, - 0.4}, v {3.6, 1.7, - 1.6, - 0.5} \end{matrix}$ 。

采用各向同性缩放保持坐标点坐标变换的一致性, 使每个点到上述平移变换坐标原点的平均距离等于 $\sqrt{2}$ , 即4点构成的圆的半径为1。缩放系数 $\begin{matrix} C_{P} 、 C_{I} \end{matrix}$ 可以通过式(6)计算:

$\begin{matrix} \{\begin{matrix} C_{P} \frac{1}{4} \overset{4}{\sum_{k = 1}} \sqrt{x_{Tk}^{2} + y_{Tk}^{2}} = \sqrt{2} \\ C_{I} \frac{1}{4} \overset{4}{\sum_{k = 1}} \sqrt{u_{Tk}^{2} + v_{Tk}^{2}} = \sqrt{2} \end{matrix} (6) \end{matrix}$

缩放变换后各点的坐标为:

$\begin{matrix} P_{C} = [\begin{matrix} x_{C} \\ y_{C} \end{matrix}] = C_{P} [\begin{matrix} x_{T} \\ y_{T} \end{matrix}]; I_{C} = [\begin{matrix} u_{C} \\ v_{C} \end{matrix}] = C_{I} [\begin{matrix} u_{T} \\ v_{T} \end{matrix}] (7) \end{matrix}$

2.2 校正图像输出

上述计算过程经空间坐标变换恢复了像点 $I (u, v)$ 在空间平面 $Π_{1}$ 上的坐标 $\begin{matrix} P (x, y), \end{matrix}$ 但是每个点的色彩并没有恢复。此时, 输出图像仅是各个点的坐标信息, 无法看到图像场景信息。

RGB图像使用3个一组的数据表达每个像素的颜色, 即其中的红色、绿色和蓝色分量^[18]。通过图像像素值的映射, 为每个点赋予RGB图像各颜色分量的灰度值, 可实现校正图像的输出。

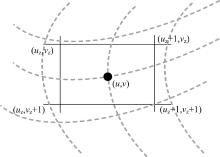
本文综合考虑计算速度和插值效果, 采用双线性插值法进行校正图像输出, 将输出像素逐个映射回输入图像中。如图3所示, 输出图像点的像素值为输入图像中距离它最近的2× 2邻域内4个点的像素灰度值的加权平均值。

	Figure Option View Download New Window
	图3 双线性插值Fig.3 Bilinear interpolation

假设校正输出图像中的任意一点 $P (x, y)$ , 使用式(1)由矩阵 $H$ 计算其对应的输入图像中的像点 $I (u, v)$ 。若 $u$ 和 $v$ 的值恰好为正整数, 则 $P (x, y) = I (u, v)$ ; 若 $u$ 和 $v$ 的值不为正整数, 则分别对 $u$ 和 $v$ 的值取整, 记为 $u_{z}$ 和 $\begin{matrix} v_{z}, P (x, y) \end{matrix}$ 的值为:

$\begin{matrix} \{\begin{matrix} I (u, v_{z}) = I (u_{z}, v_{z}) + u [I (u_{z} + 1, v_{z}) - \\ I (u_{z}, v_{z})] \\ I (u, v_{z} + 1) = I (u_{z}, v_{z} + 1) + \\ u [I (u_{z} + 1, v_{z} + 1) - I (u_{z}, v_{z} + 1)] \\ P (x, y) = I (u, v) = I (u, v) + \\ v [I (u, v_{z} + 1) - I (u, v_{z})] \end{matrix} (8) \end{matrix}$

为了达到更好的输出效果, 也可以采用双三次插值方法计算输出图像的像素值。

2.3 改进四点法的算法

通过以上论述, 将改进的四点法总结如下:

(1)在空间平面 $Π_{1}$ 和摄像机的数字图像平面 $Π_{2}$ 上分别选择4对物点 $P_{k} (x_{k}, y_{k})$ 和对应的像点 $\begin{matrix} I_{k} (u_{k}, v_{k}), \end{matrix}$ 其中任意3点不共线。

(2)运用式(5)(6)(7)对选择的上述4点做归一化处理, 处理后点的坐标为 $P_{Ck} (x_{Ck}, y_{Ck})$ 和点 $\begin{matrix} I_{Ck} (u_{Ck}, v_{Ck}) 。 \end{matrix}$

(3)运用式(4), 采用归一化处理后的坐标求解向量 $\begin{matrix} h 。 \end{matrix}$

(4)由向量 $h$ 构建射影变换矩阵 $H$ , 同时计算 $\begin{matrix} H^{- 1} 。 \end{matrix}$

(5)运用式(1), 由矩阵 $H$ 计算空间平面 $Π_{1}$ 上的物点 $P_{C} (x_{C}, y_{C})$ 对应的像点 $I_{C} (u_{C}, v_{C})$ , 由矩阵 $H^{- 1}$ 计算摄像机的数字图像平面 $Π_{2}$ 上的像点 $I_{C} (u_{C}, v_{C})$ 对应的物点 $\begin{matrix} P_{C} (x_{C}, y_{C}) 。 \end{matrix}$

(6)运用式(5)(6)(7)对上述计算的物点 $P_{C} (x_{C}, y_{C})$ 和像点 $I_{C} (u_{C}, v_{C})$ 做还原计算, 恢复物点 $P (x, y)$ 和像点 $\begin{matrix} I (u, v) 。 \end{matrix}$

(7)运用式(8)计算输出图像中各点的像素值, 输出校正图像。

(8)在输出的校正图像上提取待测点, 测量所需距离信息。

3 方法构成

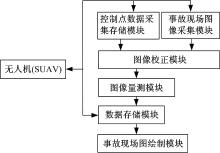
小型无人机具有4个呈十字形交叉结构的螺旋桨, 携带焦距为11.9 mm, 分辨率为1600× 1200像素的高清摄像头, 如图4所示。它可以垂直起降, 也能实现空中悬停, 同时能将空中画面实时传回控制终端。基于此方法的交通事故现场勘查系统构成如图5所示。

	Figure Option View Download New Window
	图4 小型无人机Fig.4 Small unmanned aircraft vehicles

	Figure Option View Download New Window
	图5 系统框架图Fig.5 Framework of system

为实现上述方法, 以Matlab软件^[19]编写了应用程序ImAR, 其所运行的电脑配置为:处理器为Intel(R) Core(TM) i3-2350M CPU 2.30 GHz, 内存为2.00 GB, 操作系统为Win7 64位操作系统。

4 案例分析

采用由上述改进的四点法、SUAV和ImAR软件程序构成的系统, 分别对实验控制场和交通事故现场进行数据测量试验, 与普通数码相机采集图像进行数据测量相对比, 验证本方法在交通事故现场勘测中的优势。普通数码相机为Canon PowerShot A480, 焦距为40 mm, 分辨率为1600× 1200像素, 图像大小为2 MB。普通数码相机的拍摄高度为1.5 m, SUAV的拍摄高度为15 m。

4.1 控制场实验

选择包含有边长为60 cm正方形瓷砖的地面区域建立控制场。用于数据对比分析的相邻瓷砖的交点已经用数字标出, 并且两幅图像中相同的点用同一数字标识, 点“ 0” 为原点, 其坐标设置为(100, 100), 点“ 0→ 6” 的方向为y轴方向,点"0→4"的方向为x轴方向。使用普通数码相机和SUAV拍摄的图像如图6所示。控制场中各点的坐标如表1所示。

	Figure Option View Download New Window
	图6 控制场图像Fig.6 Control field image

表1 控制场各点坐标及对应的像素坐标 Table 1 Coordinate and pixel of each control point

图6中0、1、2、3号点选为控制点, 0~6号的所有点为待测点, 分别对图6(a)和图6(b)做图像校正, 校正后的图像如图7所示。

	Figure Option View Download New Window
	图7 校正的图像Fig.7 Rectified image

在改进的四点法计算过程中, 控制点经归一化处理后, 图7(a)和图7(b)的系数矩阵分别为 $\begin{matrix} K_{a} 和 K_{b}, \end{matrix}$ 其条件数分别为4.7215和4.9946, 有效控制了矩阵的病态情况。

$\begin{matrix} \begin{matrix} K_{a} = \\ [\begin{matrix} - 1.0000 & - 1.0000 & 1 & 0 & 0 & 0 & - 0.7692 & - 0.7692 \\ 1.0000 & - 1.0000 & 1 & 0 & 0 & 0 & 1.6405 & - 1.6405 \\ 1.0000 & 1.0000 & 1 & 0 & 0 & 0 & - 0.5922 & - 0.5922 \\ - 1.0000 & 1.0000 & 1 & 0 & 0 & 0 & 1.8175 & - 1.8175 \\ 0 & 0 & 0 & - 1.0000 & - 1.0000 & 1 & 0.8722 & 0.8722 \\ 0 & 0 & 0 & 1.0000 & - 1.0000 & 1 & 0.3270 & - 0.3270 \\ 0 & 0 & 0 & 1.0000 & 1.0000 & 1 & 0.7899 & 0.7899 \\ 0 & 0 & 0 & - 1.0000 & 1.0000 & 1 & 0.2448 & - 0.2448 \end{matrix}] (9) \\ K_{b} = \\ [\begin{matrix} - 1.0000 & - 1.0000 & 1 & 0 & 0 & 0 & - 0.0097 & - 0.0097 \\ 1.0000 & - 1.0000 & 1 & 0 & 0 & 0 & - 2.0825 & 2.0825 \\ 1.0000 & 1.0000 & 1 & 0 & 0 & 0 & - 0.0000 & - 0.0000 \\ - 1.0000 & 1.0000 & 1 & 0 & 0 & 0 & - 2.0922 & 2.0922 \\ 0 & 0 & 0 & - 1.0000 & - 1.0000 & 1 & 0.8853 & 0.8853 \\ 0 & 0 & 0 & 1.0000 & - 1.0000 & 1 & 0.1861 & - 0.1861 \\ 0 & 0 & 0 & 1.0000 & 1.0000 & 1 & 0.5855 & 0.5855 \\ 0 & 0 & 0 & - 1.0000 & 1.0000 & 1 & - 0.1137 & 0.1137 \end{matrix}] (10) \end{matrix} \end{matrix}$

选择待测点之间的距离值做比较, 计算值、误差和平均误差如表2所示。

表2 待测点之间的距离和误差 Table 2 Distance and error of points

由图7可见, 使用SUAV拍摄的图像校正后包含的控制场有效区域扩大, 校正失真小, 图像输出效果好; 而使用普通数码相机拍摄的图像校正后控制点2、4、5、6号点周边包容区的图像严重失真。

由表2可见, 使用SUAV拍摄的图像校正后待测目标距离的计算值最大误差为0.80%, 平均误差为0.38%; 作为对比, 使用普通数码相机拍摄的图像校正后待测目标距离的计算值最大误差为6.04%, 平均误差为2.53%。使用SUAV拍摄的图像校正后待测目标距离的计算值更精确, 平均误差更小。使用普通数码相机拍摄的图像校正后, 与控制点距离近和在现场标定区域内的点之间的距离的计算值平均误差小, 如0和1号点、1和2号点; 在现场标定区域外内的点之间距离的计算值平均误差大, 如4和5号点、6和0号点。所以, 使用SUAV拍摄控制场的图像, 用于校正, 其待测目标的距离的计算精确度优于使用普通数码相机拍摄的情况, 而且标定区域以外的现场也可以得到有效校正。

4.2 典型案例

图8所示的照片为发生于2014年某日某时的交通事故。车辆在路面留下两条制动痕迹。在事故现场待测区域周围置放标定物后, 操纵SUAV从距离地面20 m的空中拍摄现场照片。本案例测量的主要目标是包括车辆停止位置和制动痕迹长度的现场, 以便于分析车辆制动初速度等事故信息。

	Figure Option View Download New Window
	图8 SUAV拍摄的事故现场照片Fig.8 Photo of accident site taken by SUAV

为了便于分析比较, 该案例同时采用人工测量方法和“ 改进四点法” 进行事故现场勘测。“ 改进四点法” 对交通事故现场照片进行校正后的图像如图9所示。

	Figure Option View Download New Window
	图9 事故现场校正图像Fig.9 Rectified image of traffic accident site

在事故现场校正图像中, 标出了制动拖印长度、车道宽和车辆与路边的距离等信息。由图9可看出, 校正后的图像失真小, 各标定物外延区域也得到了较好的校正。人工测量方法与本文方法的主要测量数据对比如表3所示。

表3 本文方法与人工测量方法的对比 Table 3 Comparison of measurements between the hand-on method and proposed method

由表3可见, 与人工测量方法相比, 本文方法的测量结果相对误差在4%以内, 完全能够满足交通事故现场勘查的要求, 可提高交通事故现场摄影勘测精度, 证明了采用SUAV由“ 改进四点法” 进行道路交通事故现场勘查的可行性。

5 结束语

采用普通数码相机运用“ 四点法” 勘查交通事故现场时, 相机的拍摄角度小, 拍摄场景前小后大, 远处目标模糊, 由此带来图像校正精度低、场景覆盖面小、可用信息恢复少等缺点。本文提出了基于小型无人机摄影测量的“ 改进四点法” 。该方法采用预先对控制点信息进行归一化处理的方式来减少图像校正过程中病态矩阵计算的影响, 提高了图像测量算法精度。在此基础上, 通过编写程序对空中摄影图像进行二维校正、测量、记录和标注。通过控制场试验和典型交通事故案例分析验证了该方法的有效性。与使用普通数码相机手持摄影测量的方法相比, 使用该方法进行交通事故现场勘查不但可以在单幅图像勘测中扩展勘查范围, 有效抑制拍摄角度对“ 四点法” 的影响, 而且还能提高事故现场勘查的精度, 增强其实用性。

小型无人机摄影测量用于交通事故现场勘查也有一定的局限性。SUAV在大风、雨、雪和雾等极端天气条件下使用, 其稳定性和精度受影响较大。同时, 为了提高事故勘查的精度, 需要预设地面标志物, 将已知参数标志物布设在待测区域周围, 并且在拍摄的图像中能够识别。如校正图像(图9)中, 距离标定物越远, 数据测量误差越大, 最上部车道宽度已变成346.64 cm, 相对误差为6.7%。这些都是下一步将要解决的问题。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	杨博, 金先龙, 张晓云, 等. 基于数字化摄影测量的交通事故信息采集和过程再现[J]. 汽车工程, 2010, 32(6): 530-534, 546. Yang Bo, Jin Xian-long, Zhang Xiao-yun, et al. Information acquisition and process reconstruction of traffic accidents based on digitial photogrammetry[J]. Automotive Engineering, 2010, 32(6): 530-534, 546. [本文引用:1]
[2]	田建, 李江, 李亚桥. 道路交通事故现场摄影测量的标定技术[J]. 吉林大学学报: 工学版, 2006, 36(增刊1): 136-139. Tian Jian, Li Jiang, Li Ya-qiao. Calibration technique of photogrammetry of traffic accident scene[J]. Journal of Jilin University( Engineering and Technology Edition), 2006, 36(Sup. 1): 136-139. [本文引用:1]
[3]	杨亚威, 李俊山, 张士杰, 等. 基于视觉对比敏感度与恰可察觉失真感知的图像复原[J]. 光学精密工程, 2014, 22(2): 459-466. Yang Ya-wei, Li Jun-shan, Zhang Shi-jie, et al. Image restoration based on visual contrast sensitivity and just noticeable distortion perception[J]. Optics and Precision Engineering, 2014, 22(2): 459-466. [本文引用:1]
[4]	柯洪昌, 孙宏彬. 图像序列的显著性目标区域检测方法[J]. 中国光学, 2015, 8(5): 768-774. Ke Hong-chang. Sun Hong-bin, A saliency target area detection method of image sequence[J]. Chinese Optics, 2015, 8(5): 768-774. [本文引用:1]
[5]	张来刚, 魏仲慧, 何昕, 等. 多约束融合算法在多摄像机测量系统中的应用[J]. 液晶与显示, 2013, 28(4): 608-614. Zhang Lai-gang, Wei Zhong-hui, He Xin, et al. Multi-camera measurement system based on multi-constraint fusion algorithm[J]. Chinese Journal of Liquid Crystal and Displays, 2013, 28(4): 608-614. [本文引用:1]
[6]	鲁光泉, 胡楠, 李一兵. 道路交通事故现场平面直线参数的摄影测量重建方法[J]. 交通运输工程学报, 2010, 10(3): 118-121. Lu Guang-quan, Hu Nan, Li Yi-bing. Reconstruction method of line parameters in traffic accident scene plane by photogrammetry[J]. Journal of Traffic and Transportation Engineering, 2010, 10(3): 118-121. [本文引用:1]
[7]	Cliff W E, MacInnis D D, Switzer D A. An evaluation of rectified bitmap 2D photogrammetry with PC-Rect[C]∥SAE Paper, 970952. [本文引用:1]
[8]	Switzer D, Cand rlic T. Factors affecting the accuracy of non-metric analytical 3-D photogrammetry, using photoModeler[C]∥SAE Paper, 1999-01-0451. [本文引用:1]
[9]	iWitness Close Range Photogrammetry. Accuracy performance of the close-range photogrammetry system iWitness: results of a measurement comparison with a surveying total station[EB/OL]. [2014-06-08]. http://www.iwitnessphoto.com/iwitness/accuracy_study3.html. [本文引用:1]
[10]	Erickson M S, Bauer J J, Hayes W C. The accuracy of photo-based three-dimensional scanning for collision reconstruction using 123D Catch[C]∥SAE Paper, 2013 -01-0784. [本文引用:1]
[11]	Rand les B, Jones B, Welcher J, et al. The accuracy of photogrammetry vs. hand -on measurement techniques used in accident reconstrucion[C]∥SAE Paper, 2010-01-0065. [本文引用:1]
[12]	Wang G, Hu Z, Wu F, et al. Single view metrology from scene constraints[J]. Image and Vision Computing, 2005, 23(9): 831-840. [本文引用:2]
[13]	苗新强, 金先龙. 基于图像引导的交通事故现场实时测绘方法[J]. 上海交通大学学报, 2013, 47(2): 253-258. Miao Xin-qiang, Jin Xian-long. Real time mapping for traffic accident scene based on image guide[J]. Journal of Shanghai Jiao Tong University, 2013, 47(2): 253-258. [本文引用:1]
[14]	王丰元, 杨朝会, 邹旭东, 等. 基于道路标线的交通事故现场摄影测量研究[J]. 交通运输工程与信息学报, 2008, 6(1): 1-5. Wang Feng-yuan, Yang Zhao-hui, Zou Xu-dong, et al. Application of photogrammetry in traffic accident scene measurement based on road mark[J]. Journal of Transportation Engineering and Information, 2008, 6(1): 1-5. [本文引用:1]
[15]	李少龙, 蒋国辉. 天宝X100无人机摄影测量试验[J]. 测绘通报, 2013(8): 120-121. Li Shao-long, Jiang Guo-hui. The photogrammetry test of Trimble X10UAV[J]. Bulletin of Surveying and Mapping, 2013(8): 120-121. [本文引用:1]
[16]	韩学源, 金先龙, 张晓云, 等. 基于视频图像与直接线性变换理论的车辆运动信息重构[J]. 汽车工程, 2012, 34(12): 1145-1149. Han Xue-yuan, Jin Xian-long, Zhang Xiao-yun, et al. Vehicle movement information reconstruction based on video images and DLT theory[J]. Automotive Engineering, 2012, 34(12): 1145-1149. [本文引用:1]
[17]	Hartley R I. In defense of the eight-point algorithm[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1997, 19(6): 580-593. [本文引用:1]
[18]	郝亮, 邓希宁, 刘斌, 等. RGB 格式彩色图像重建算法的研究[J]. 激光与红外, 2013, 43(2): 229-232. Hao Liang, Deng Xi-ning, Liu Bin, et al. Research reconstructed algorithm of RGB format color image[J]. Laser & Infrared, 2013, 43(2): 229-232. [本文引用:1]
[19]	贾苏娟, 韩广良, 陈小林, 等. 光度非均匀彩色序列图像超分辨率重建[J]. 液晶与显示, 2014, 29(1): 106-113. Jia Su-juan, HanN Guang-liang, Chen Xiao-lin, et al. Super-resolution reconstruction with photometric change of color image sequence[J]. Chinese Journal of Liquid Crystal and Displays, 2014, 29(1): 106-113. [本文引用:1]
[20]	赵金玲, 刘学锋. 基于 MATLAB 的遥感数字图像几何校正方法[J]. 测绘与空间地理信息, 2003, 26(2): 24-25. Zhao Jin-ling, Liu Xue-feng. The methodology of geometrically correction about remote sensing digital image based on MATLAB[J]. Geomatics & Spatial Information Technology, 2003, 26(2): 24-25. [本文引用:1]

2010

0.0

. 2010, 32(6):530-534, 546

Information acquisition and process reconstruction of traffic accidents based on digitial photogrammetry

基于数字化摄影测量的交通事故信息采集和过程再现

Yang Bo , Jin Xian-long , Zhang Xiao-yun

杨博, 金先龙, 张晓云

针对目前交通事故信息采集和过程再现存在的不足,建立了基于二维和三维直接线性变换法的摄影测量模型,分别采用两种方案对目标物进行三维重建的实验和结果的对比分析.以一起真实交通事故为例,运用摄影测量方法采集现场路面和车身变形的信息.以路面信息为事故再现的输入数据,求解事故车辆碰撞瞬时速度;以车身变形信息为评判依据,验证所求车速.重建结果表明,摄影测量方法可提高交通事故信息采集效率和事故再现精度.

... 这需要占用事故现场路段、中断交通,容易诱发二次交通事故,且存在费时长、现场信息遗漏多、勘测精度低,现场量测的数据和绘制的草图因操作者存在差异,以及恢复交通后无法对现场复查勘测等缺陷,给事故责任判断造成很大麻烦^[1,2] ...

2006

0.0

. 2006, 36(增刊1):136-139 DOI:doi:10.3969/j.issn.1671-5497.2006.03.031

Calibration technique of photogrammetry of traffic accident scene

道路交通事故现场摄影测量的标定技术

Tian Jian , Li Jiang , Li Ya-qiao

田建, 李江, 李亚桥

Based on analysis of the calibration method of threedimensioned photogrammetry, a new method of camera calibration using planar patterns was proposed.After several photos were obtained from different views, a linear solution was derived, followed by a nonlinear refinement based on the maximum likelihood criterion, the final parameters of the model were achieved. The experiment results demonstrate the proposed method is not only simple and accurate, but also flexible.

在分析三维摄影测量标定方法的基础上，提出了基于平面模板的照相机标定方法，即从不同视点拍摄多幅现场图像，先进行线性求解，然后基于极大似然准则进行非线性优化，获得照相机模型参数。实验结果表明该方法标定精度高，标定物简单，更加灵活易用。

2014

0.0

... 在交通事故现场拍摄的照片(图像)中包含有现场大量信息,如车辆停止位置、制动拖印、轮胎印迹、油污迹、碎片散落分布位置等^[3,4] ...

2015

0.0

. 2015, 8(5):768-774 DOI:doi:10.3788/CO.20150805.0768

A saliency target area detection method of image sequence

图像序列的显著性目标区域检测方法

Ke Hong-chang.Sun Hong-bin

柯洪昌, 孙宏彬

摘　要：针对传统视觉显著性模型在自顶向下的任务指导和动态信息处理方面的不足,设计并实现了融入运动特征的视觉显著性模型。利用该模型提取了图像的静态特征和动态特征,静态特征的提取在图像的亮度、颜色和方向通道进行,运动特征的提取采用基于多尺度差分的特征提取方法实现,然后各通道分别通过滤波、差分得到显著图,在生成全局显著图时,提出多通道参数估计方法,计算图像感兴趣区域与眼动感兴趣区域的相似度,从而可在图像上准确定位目标位置。针对20组视频图像序列（每组50帧）进行了实验,结果表明：本文算法提取注意焦点即目标区域的平均相似度为0.87,使用本文算法能够根据不同任务情境,选择各特征通道的权重参数,从而可有效提高目标搜索的效率。

... 在交通事故现场拍摄的照片(图像)中包含有现场大量信息,如车辆停止位置、制动拖印、轮胎印迹、油污迹、碎片散落分布位置等^[3,4] ...

2013

0.0

. 2013, 28(4):608-614 DOI:doi:10.3788/YJYXS20132804.0608

Multi-camera measurement system based on multi-constraint fusion algorithm

多约束融合算法在多摄像机测量系统中的应用

Zhang Lai-gang , Wei Zhong-hui , He Xin

张来刚, 魏仲慧, 何昕

In order to improve three-dimensional measurement accuracy in the large field and to overcome the shortcomings of the traditional bundle adjustment algorithm for image correction being not ideal for large field of view (the control points concentrated in the center of the view), this paper presented a multi-camera 3D measurement methods based on multi-constraint fusion algorithm. The basic idea is collinear equation of three-dimensional space coordinates of the control points and corresponding pixel coordinates is looked as constraints, using the known distance constraint, three-point collinear, four-point coplanar to establish the restriction between coordinates of the control points and pixel points, thus completing the three-dimensional coordinate measurement, at the same time, achieving the online calibration of the system parameters. In the experiment, the RMS error and relative accuracy of distance are used to analyses the measurement accuracy, the relative accuracy of distance reaches to 1:7 000~1:15 000, compared to the traditional bundle adjustment algorithm, the measurement accuracy of this algorithm is improved an order of magnitude, it is a reliable high-precision vision measurement method.

为了提高大视场三维测量精度,克服传统束调整算法对大视场图像校正不理想(控制点集中在视场中心)的缺点,提出了基于多约束融合算法的多摄像机三维测量方法,其基本思想为:将空间控制点的三维坐标与其对应像素点坐标之间的共线方程作为约束条件,利用已知的距离、三点共线和四点共面等信息,建立测量视场中控制点与像点坐标间的约束关系,从而完成三维坐标测量,同时实现了系统参数的在线标定。实验中,通过RMS误差和测距相对精度对测量精度进行了定量分析,测距相对精度达到了1:7 000~1:15 000,相对传统的束调整算法,该算法测量精度提高了一个数量级,是一种可靠的高精度视觉测量方法。

... 目前,为了实现摄影图像校正测量,出现了一些商用软件,如PC-RECT、PhotoModeler、iWitness和123D Catch等^[5,6,7,8,9] ...

2010

0.0

. 2010, 10(3):118-121

Reconstruction method of line parameters in traffic accident scene plane by photogrammetry

道路交通事故现场平面直线参数的摄影测量重建方法

Lu Guang-quan , Hu Nan , Li Yi-bing

鲁光泉, 胡楠, 李一兵

以空间直线的三维重建原理为基础,通过现场空间直线段在摄影测量系统空间下的三维重建,实现了道路交通事故现场图绘制平面的最小中值二乘拟合,并完成了现场空间直线从摄影测量系统空间向道路交通事故现场图绘制平面的转换,实现了道路交通事故现场平面直线参数的检测和重建。对摄影测量系统世界坐标系下现场图平面、中心线及左、右边缘线的三维重建进行了试验,并得到了中心线及左、右边缘线在现场图平面上的投影直线方程和投影图。试验结果表明:左、右边缘线和中心线在现场图平面上的投影与x轴的夹角之差均小于0.1°,道路的边缘线与中心线基本平行,测量精度较好。

... 目前,为了实现摄影图像校正测量,出现了一些商用软件,如PC-RECT、PhotoModeler、iWitness和123D Catch等^[5,6,7,8,9] ...

0.0

... 目前,为了实现摄影图像校正测量,出现了一些商用软件,如PC-RECT、PhotoModeler、iWitness和123D Catch等^[5,6,7,8,9] ...

1999

0.0

... 目前,为了实现摄影图像校正测量,出现了一些商用软件,如PC-RECT、PhotoModeler、iWitness和123D Catch等^[5,6,7,8,9] ...

2014

0.0

... 目前,为了实现摄影图像校正测量,出现了一些商用软件,如PC-RECT、PhotoModeler、iWitness和123D Catch等^[5,6,7,8,9] ...

2013

0.0

... 的二维校正算法,是计算机视觉算法领域的重要分支^{[10,11,12,13]},可用于一般平面现场数据的测量 ...

2010

0.0

... 的二维校正算法,是计算机视觉算法领域的重要分支^{[10,11,12,13]},可用于一般平面现场数据的测量 ...

2005

0.0

... 的二维校正算法,是计算机视觉算法领域的重要分支^{[10,11,12,13]},可用于一般平面现场数据的测量 ...

... 1 小孔模型所有景物通过摄像机光轴中心点投射到成像平面上的摄像机模型,称为小孔模型^[12] ...

2013

0.0

. 2013, 47(2):253-258

Real time mapping for traffic accident scene based on image guide

基于图像引导的交通事故现场实时测绘方法

Miao Xin-qiang , Jin Xian-long

苗新强, 金先龙

In order to meet the needs of mapping the accident scene diagram on the scene for traffic police, a real time mapping method for traffic accident scene investigation based on image guide was proposed. The proposed procedure consists of a transformation which transforms a single photo of the accident scene from perspective image to orthographic image using direct linear transformation method, followed by mapping accident scene information such as vehicles, bodies, fall out objects, braking traces and so on directly over the orthographic image, and finally printing out the accident scene diagram, which needs to be signed by interested parties. A typical traffic accident case was used to validate the proposed method. Compared with the traditional handson measurement, the proposed method can not only improve the accuracy of site investigation, but also can considerably reduce the time of onscene data processing and drawing, which contributes to satisfying the requirement of printing out the accident scene diagram in real time.

为了满足交警现场绘制事故现场图的实际需要，提出了基于图像引导的交通事故现场实时测绘方法.首先根据直接线性变换法将事故现场照片由透视图转换为正投影图像；然后直接在正投影图像上进行车辆、人体、散落物和刹车痕迹等事故现场信息的绘制和相关尺寸的标注；最后实现现场图的打印输出并由当事人签字确认.通过典型交通事故案例验证了该方法的有效性.和传统手工测绘相比，该方法在提高事故现场勘测精度的同时，还能大大缩短数据处理和现场绘图时间，满足实时打印输出现场图的要求.

... 的二维校正算法,是计算机视觉算法领域的重要分支^{[10,11,12,13]},可用于一般平面现场数据的测量 ...

2008

0.0

. 2008, 6(1):1-5 DOI:doi:10.3969/j.issn.1672-4747.2008.01.001

Application of photogrammetry in traffic accident scene measurement based on road mark

基于道路标线的交通事故现场摄影测量研究

Wang Feng-yuan , Yang Zhao-hui , Zou Xu-dong

王丰元, 杨朝会, 邹旭东

摘　要：论述了基于普通相机的交通事故现场测量技术基本理论，提出了一种利用道路标线作为标定参考物的新的标定方法，在小波多尺度边缘检测基础上，利用Harris角点提取对图像进行分析处理，对影响摄影测量精度的有关参数进行了简要描述，对一个实际事故现场的部分数据进行了分析，验证了设计的算法。

... 理想的拍摄角度应垂直于地面^[14],这在采用普通相机人工拍摄方法中实际上无法达到 ...

2013

0.0

. 2013, (8):120-121

The photogrammetry test of Trimble X100 UAV

天宝X100无人机摄影测量试验

Li Shao-long , Jiang Guo-hui

李少龙, 蒋国辉

一、引言近年来,无人机(unmanned aerial vehicles,UAV)摄影测量技术发展迅速,在大比例尺地形图测绘领域得到了广泛应用.尽管如此,无人机操控难度大、数据处理过程复杂等因素在很大程度上制约了该技术的应用. 美国Trimble公司旗下Gatewing公司推出的无人机X100(天鹰)机身轻小、操作简便,国外的测试结果表明其摄影测量成果数据精度可达到平面5 cm、高程10 cm的水平.为了测试其性能,笔者选取一个面积约1 km2的公园作为试验区,利用X100实地采集航空影像,经空三处理后利用检查点对比计算其精度,分析和评价X100应用于大比例尺地形图测绘的可行性和适用性.

... 近来,小型无人机(Small unmanned aircraft vehicles,SUAV)摄影测量技术迅速发展^[15],在大比例尺地形图测绘领域得到了广泛应用 ...

2012

0.0

. 2012, 34(12):1145-1149 DOI:doi:10.3969/j.issn.1000-680X.2012.12.017

Vehicle movement information reconstruction based on video images and DLT theory

基于视频图像与直接线性变换理论的车辆运动信息重构

Han Xue-yuan , Jin Xian-long , Zhang Xiao-yun

韩学源, 金先龙, 张晓云

运用摄影测量中的直接线性变换理论,并根据事故现场的标记点信息,解得正投影变换的二维直接线性变换系数。通过对事故监控视频进行解帧得到相片组,在解帧相片组上标记车轮与道路的接触点,并对车轮标记点进行正投影。由标记点拟合出轨迹曲线,再通过积分求得轨迹曲线的长度,结合视频的帧频信息,进而求得肇事车辆的车速等。以一起真实交通事故为例,运用该方法,求得其运行轨迹长度和车速等数据。

... 当图像中4个任意三点不共线的参考点的像素坐标及其在空间平面上的坐标已知时,就能够确定图像上的点和空间平面上的点的一一对应关系^[16] ...

1997

0.0

... 为了避免上述问题,在使用方程(4)计算前,先对物点和像点坐标值采用平移和缩放变换,进行归一化处理^[17],如图2所示 ...

2013

0.0

. 2013, 43(2):229-232 DOI:doi:10.3969/j.issn.1001-5078.2013.02.025

Research reconstructed algorithm of RGB format color image

RGB 格式彩色图像重建算法的研究

Hao Liang , Deng Xi-ning , Liu Bin

郝亮, 邓希宁, 刘斌

从原始图像到最终形成的真彩色图像的变换过程,称为彩色图像重建.介绍了几种现在常用的彩色图像重建技术的插值算法,提出了一个改进的彩色图像重建的算法.通过MATLAB仿真比较重建图像的质量,发现用改进的算法重建的图像质量比其他算法重建的图像质量要好.

... RGB图像使用3个一组的数据表达每个像素的颜色,即其中的红色、绿色和蓝色分量^[18] ...

2014

0.0

. 2014, 29(1):106-113 DOI:doi:10.3788/YJYXS20142901.0106

HanN Guang-liang, Chen Xiao-lin, et al. Super-resolution reconstruction with photometric change of color image sequence

光度非均匀彩色序列图像超分辨率重建

Jia Su-juan

贾苏娟, 韩广良, 陈小林

In order to realize the super-resolution reconstruction of color sequence images when the external illumination changes or the camera adjusts integration time automatically, an algorithm has been proposed. Firstly, the images' histograms of oriented gradients (HOG) are extracted as the matching characters and the correlation coefficient is used as the similarity measurements for geometric registration. Secondly, a photometric model is established to achieve photometric registration. Finally, the algorithm of Maximum a Posteriori (MAP) is adopted to get high-resolution images. In order to show the advantage of the algorithm, the results of the average gradient, information entropy and image contrast metric (ICM) of reconstructed images are given. The results show that the average gradient and information entropy of these high-resolution images are enhanced significantly and images have more information. The algorithm is robust to photometric change and it can obviously reduce the photometric difference between the reconstructed images and improve the contrast of color images.

为了实现外界光照变化或相机积分时间自动调节等情况下拍摄的彩色序列图像的超分辨率重建，文章首先提取图像感兴趣区域的方向梯度直方图作为匹配特征，以相关系数作为相似性测度进行几何配准；其次建立光度测量模型进行光度配准；最后采用最大后验估计算法求出光度改善的高分辨率图像。文章采用平均梯度、信息熵、图像对比度对重建图像质量进行评估。实验表明，重建后高分辨率图像平均梯度及信息熵均有大幅提高，图像更清晰、信息更丰富。算法能有效减小重建图像间的光度差异，提高彩色图像的对比度，对光度变化具有一定的鲁棒性。

... 为实现上述方法,以Matlab软件^[19]编写了应用程序ImAR,其所运行的电脑配置为:处理器为Intel(R) Core(TM) i3-2350M CPU 2 ...

2003

0.0

. 2003, 26(2):24-25 DOI:doi:10.3969/j.issn.1672-5867.2003.04.006

The methodology of geometrically correction about remote sensing digital image based on MATLAB

MATLAB 的遥感数字图像几何校正方法

Zhao Jin-ling , Liu Xue-feng

赵金玲, 刘学锋, . 基于

MATLAB将数值计算、可视化和编程集于一体,是一种高效的工程计算与编程语言,而遥感数字图像的几何校正过程中包含着很多的数值计算,本文介绍了应用MATLAB进行这些数值计算的方法,通过其简单、高效的编程方式,说明了MATLAB在遥感影像处理方面的独到之处,为遥感影像处理提供了一种新思路.