基于热流固耦合过程的液力缓速器叶片强度分析

引用本文

袁哲, 徐东, 刘春宝, 李雪松, 李世超. 基于热流固耦合过程的液力缓速器叶片强度分析. 2016, 46(5): 1506-1512
YUAN Zhe, XU Dong, LIU Chun-bao, LI Xue-song, LI Shi-chao. Strength analysis of hydraulic retarder blade based on the process of thermal-fluid structure interaction. Journal of Jilin University Engineering and Technology Edition, 2016, 46(5): 1506-1512 复制到剪切板

Permissions

基于热流固耦合过程的液力缓速器叶片强度分析

袁哲¹, 徐东¹, 刘春宝¹, 李雪松², 李世超¹

1.吉林大学机械科学与工程学院,长春 130022

2.吉林大学汽车仿真与控制国家重点实验室,长春 130022

通信作者:刘春宝(1980-),男,副教授,博士.研究方向:液力传动与自动变速.E-mail:liuanbc@126.com

作者简介:袁哲(1984-),男,工程师,博士.研究方向:液力传动与自动变速.E-mail:yuanzhe@jlu.edu.cn

基金:国家自然科学基金项目(51305156)

摘要

针对传统液力缓速器叶片强度的流固耦合分析方法无法真实地模拟叶片载荷分布,以及未考虑流固耦合存在温度场的影响的问题,本文根据质量守恒、N-S、能量守恒以及非线性结构动力学,采用一种新式流固耦合方法以及考虑温度场作用的热流固耦合方法,分别对某型号液力缓速器叶片强度进行数值计算,并将两者结果从叶片位移和等效应力的角度进行对比分析。结果表明:在其他条件相同的情况下,考虑温度场对叶片的复合作用后,叶片位移和等效应力分别增大6%和21%,易引起叶片强度失效,存在安全隐患。

关键词: 流体传动与控制; 液力缓速器; 数值模拟; 叶片强度; 流固耦合; 热流固耦合

中图分类号:TH137 文献标志码:A 文章编号:1671-5497(2016)05-1506-07

Strength analysis of hydraulic retarder blade based on the process of thermal-fluid structure interaction

YUAN Zhe¹, XU Dong¹, LIU Chun-bao¹, LI Xue-song², LI Shi-chao¹

1.College of Mechanical Science and Engineering, Jilin University, Changchun 130022, China

2.State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022, China

Abstract

The traditional method of Fluid-structure Interaction (FSI) of hydraulic retarder cannot reliably simulate the load distribution on the blade, and it does not take the influence of temperature field into consideration. An efficient one-way Thermal-fluid Structure Interaction (TFSI) method is presented according to Navier-Stokes equations, energy conservation equations and nonlinear structure dynamics equation. The simulation results of FSI and TFSI under the same working condition are comparatively analyzed from the aspects of deformation and equivalent stress. The results indicate that, if other conditions are the same, the maximum displacement of the blade is increased by 6% and maximum equivalent strength is increased by 21% after considering the composite effect of temperature field on the blade boundary, which can increase the probability of strength failure of the blade and have security problems.

Keyword: turn and control of fluid; hydraulic retarder; numerical simulation; blade strength; fluid-structure interaction (FSI); thermal-fluid structure interaction (TFSI)

Show Figures

0 引言

液力缓速器具有高速制动力矩大、制动平稳、噪声小、寿命长、体积较小等优点, 在军用车辆、重型载货车以及工程机械等领域得到了广泛应用^[1]。由于液力缓速器在高速制动时, 叶片会因受到油液的冲击碰撞, 产生不同程度的形变, 从而存在断裂隐患。所以对液力缓速器叶片进行强度分析尤为重要。

因液力缓速器成本较高, 分析时主要采取数值模拟, 如流固耦合。流固耦合的传统方法^{[2, 3, 4]}可总结为利用Matlab对Fluent求得的叶片表面的压力分布点进行坐标变换、曲面拟合, 获取该叶片表面的液压载荷分布, 再按线性分布加载到ANSYS生成的相应叶片FEA模型上进行叶片强度分析。然而, 应用此方法对有限元模型施加载荷时, 以沿旋转半径方向的线性分布载荷模拟分布在叶片上的载荷, 这未能真实体现出液体总压在叶片压力面上的分布, 因为考虑到油液的黏性、油液与壁面的边界层处理和叶片非压力面的背压等因素的影响, 叶片上的压力分布是无规律可循的^[2]。另外, 在坐标变换时的累积误差也会影响仿真结果的精度。因此, 直接将流道CFD计算结果整体加载到相应FEA模型上直接耦合是一种更真实、可靠的方法。再者, 由于高速制动时产生大量的热形成热应力, 使叶片产生热膨胀变形, 还会形成与压力场产生耦合作用的温度场, 从而加大叶片变形量。因此, 在对叶片强度分析时, 必须考虑温度场对叶片强度的复合作用, 进行热流固耦合。

对于多场耦合数值计算研究一直都是学术界的研究热点。早期航空领域的气动弹性问题^[5], 就是典型的流固耦合作用。美国国家航空航天局的Lewis研究中心对气热弹耦合进行了探索^[6], 主要研究了应用多块结构网格计算复杂几何三维黏性流场与涡轮冷却流动现象; York等^[7]利用耦合传热方法模拟了气轮机叶片在两种不同的发动机实际操作条件下的温度分布; Takahashi等^[8]采用数值模拟计算研究了由圆形表面光滑通道进行冷却的涡轮叶片的耦合传热问题; Nowak等^[9]基于热流固耦合, 搜索C3X型叶片在冷却孔数目不变的情况下, 优化最大热应力和最高温度较小的最佳冷却结构, 优化后叶片的最高温度明显低于优化前, 叶片的等效应力和温度场分布均有一定的改善; Dennis等^[10]利用约束优化方法对某直叶片进行了改善, 使得叶片表面温度分布更加均匀, 并且较大幅度地降低了热传导量。由此看来, 运用热流固多物理场耦合数值模拟方法, 进行液力缓速器叶片强度分析是十分有效可信的。

本文采用一种新式流固耦合方法以及考虑温度场作用的热流固耦合方法, 分别对某型号液力缓速器叶片强度进行数值计算, 并将两者结果从叶片位移和等效应力的角度进行了对比分析。

1 计算方法

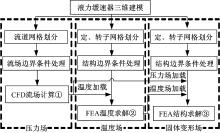
本文研究的是液力缓速器叶片强度问题, 假设叶片变形量对流场的影响较小, 采用单向热流固耦合分析叶片强度是基于内部流场计算的基础上进行的, 其多场耦合作用通过界面力起作用。图1为液力缓速器单向热流固耦合求解流程, 包括4个部分:压力场、温度场、固体变形场以及域与域之间数据传递的交界面。各个场在场内独自求解计算, 而场之间的数据传递通过交界面耦合求解。

	Figure Option View Download New Window
	图1 液力缓速器单向热流固耦合求解流程Fig.1 One-way TFSI calculation principle process of hydraulic retarder

本文中热流固耦合数值模拟计算具体过程如下:

(1)在流场域内进行流道的数值计算, 假定流体不可压, 则流动流体所需满足的方程理论有^[11]:

连续性方程:

$\begin{matrix} \nabla \cdot (ρv) = 0 (1) \end{matrix}$

式中: $\begin{matrix} \nabla \end{matrix}$ 为哈密尔顿算子; $\begin{matrix} ρ \end{matrix}$ 为流体密度, kg/m³; $\begin{matrix} v \end{matrix}$ 为流体速度, m/s。

动量方程:

$\begin{matrix} \begin{matrix} \frac{\partial (ρv)}{\partial t} + \nabla \cdot (ρvv) = - \nabla p + \nabla \cdot [μ (\nabla v + \nabla v^{T})] + \\ ρg + F + \nabla \cdot (\overset{n}{\sum_{k = 1}} α_{k} ρ_{k} v_{dr, k} v_{dr, k}) (2) \end{matrix} \end{matrix}$

式中: $\begin{matrix} μ \end{matrix}$ 为流体黏度, Pa· s; $\begin{matrix} F \end{matrix}$ 为体积力, N; $v_{dr, k}$ 为第 $\begin{matrix} k \end{matrix}$ 相的漂移速度, m/s。

工作时, 由于油液与缓速器内壁及叶片的碰撞摩擦会产生大量热能, 因此还需满足能量方程:

$\begin{matrix} \begin{matrix} \frac{\partial ρE}{\partial x} + \nabla \cdot [v (ρE + p)] = \nabla \cdot [k_{eff} \nabla T - \\ \sum_{j} h_{j} J_{j} + (τ_{eff} \cdot v)] + S_{h} (3) \end{matrix} \end{matrix}$

式中: $\begin{matrix} E \end{matrix}$ 为流体为微团的总能, J/kg; $\begin{matrix} h_{j} 为组分 j \end{matrix}$ 的焓, J/kg; k_eff为有效热传导系数, W/(m²· K); $J_{j}$ 为组分 $j$ 的扩散通量; $\begin{matrix} S_{h} \end{matrix}$ 为用户定义的体积热源项。

将方程(1)(2)(3)联立求解计算, 于是在流场域内便可计算出油液的压力和温度。

(2)将流体温度加载到定子、转子上, 在传热域进行温度场求解时, 需满足材料传热基本方程:

$\begin{matrix} Q = kAΔ t_{m} (4) \end{matrix}$

式中: $\begin{matrix} k \end{matrix}$ 为传热系数; $\begin{matrix} A \end{matrix}$ 为传热面积; Δ t_m为传热均温差。

(3)在固体变形场, 将计算得出的压力场与温度场通过耦合交界面加载到定子、转子上, 不仅需满足由流体诱发固体振动、位移的控制方程, 还需满足热流固交界面处流体与固体的位移、热流量、温度、应力等的耦合域控制方程, 故需将两者联立, 共同求解:

$\begin{matrix} M_{s} \frac{d^{2} r}{d t^{2}} + C_{s} \frac{dr}{dt} + K_{s} r + τ_{s} = 0 (5) \end{matrix}$

式中: $\begin{matrix} M_{s} \end{matrix}$ 为质量矩阵; $\begin{matrix} C_{s} \end{matrix}$ 为阻尼矩阵; $\begin{matrix} K_{s} \end{matrix}$ 为刚度矩阵; $\begin{matrix} r \end{matrix}$ 为固体位移; $\begin{matrix} τ_{s} \end{matrix}$ 为固体受到的应力。

$\begin{matrix} \begin{matrix} n \cdot τ_{f} = n \cdot τ_{s} (6) \\ r_{f} = r_{s} (7) \\ q_{f} = q_{s} (8) \\ T_{f} = T_{s} (9) \end{matrix} \end{matrix}$

式中:q为热流量; T为温度; 下标f、s分别表示流体和固体。

通过步骤(1)(2)(3)的求解计算, 即可得到定、转子所受到的变形位移和等效应力。

2 热流固耦合计算

2.1 模型的网格划分与边界条件设定

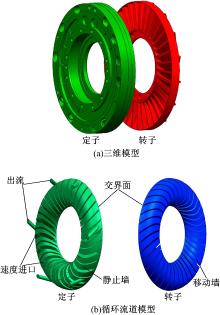
本文所研究的是扁圆形腔直叶片液力缓速器, 具体结构参数如表1所示。定子、转子材料为铸铝104, 其材料特性如下:弹性模量为80 GPa; 泊松比为0.33; 热膨胀系数为2.4× 10^-5 /℃; 热导率为155 W/(m· K); 强度极限为490 MPa; 屈服极限为350 MPa。定子、转子的三维实体模型以及油液在缓速器内的循环流道模型见图2。

表1 液力缓速器结构参数 Table 1 Geometrical parameters for hydraulic retarder

	Figure Option View Download New Window
	图2 液力缓速器模型Fig.2 Model of the hydraulic retarder

计算模型的边界条件设置如图2所示。其中进油口的边界条件为速度进口, 在定子厚叶片上; 出油口的边界条件为出流, 在定子外环上, 初始油温为60 ℃(工程实际中, 经换热器冷却后的充油温度); 定子的叶片和外环面都设置为静止墙, 转子的叶片和外环面设置为移动墙, 设置转子转速为1200 r/min, 充液率为100%; 定转子接合面采用移动网格理论, 选取的单位时间步长t=5× 10^-4 s, 不大于单位网格单元大小。液力缓速器内外环较厚, 在正常工况下的变形远小于叶片的变形, 故可视为刚性壁面。工作介质为8号液力传动油, 密度为860 kg/m³, 流体黏度为0.0258 kg/(m· s)^[12]。

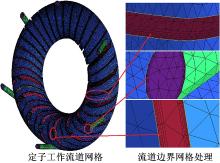
考虑油液黏性作用, 流道与壁面在边界处划分网格时采用棱柱型网格, 如图3(以定子流道为例)所示。

	Figure Option View Download New Window
	图3 定子网格处理Fig.3 Stator grid

2.2 算法与湍流模型

在Fluent中进行流场三维瞬态数值模拟流场计算过程中, 采用RNG $\begin{matrix} k - ε \end{matrix}$ 湍流模型, 流体控制方程的离散采用有限体积法, 流场仿真计算采用多流动区域耦合计算方法, 流场的数值解法采用SIMPLEC算法。计算得出的温度交由ANSYS Workbench 中的Steady-State Thermal计算温度场分布, 之后再将其与Fluent计算得出的压力场共同加载到Static Structural上计算求解。

3 强度数值计算结果对比分析

通过Fluent计算结果, 液力缓速器在高速制动时, 定子由60 ℃最高升至126 ℃, 转子由60 ℃最高升至119 ℃, 定子温升更大; 考虑到定、转子之间的力学效果差异, 选取定子作为研究对象。由于分析研究的是叶片的强度, 故在求解计算时, 固定定子壳体内壁, 在分析时只考虑叶片应力值变化。

3.1 位移对比分析

3.1.1 整体位移计算结果

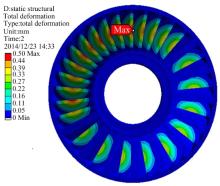
流固耦合定子位移分布如图4所示, 在整体上, 薄叶片的变形位移较明显, 厚叶片上的位移几乎没有, 由此可见, 叶片厚度对强度影响较显著。另外, 压力面上的位移比吸力面的位移大, 变形弯曲度也较明显。在局部叶片上, 位移沿叶片径向由根部到前缘呈圆弧状梯度增大, 在压力面前缘中心处位移最大, 约0.5 mm, 分析其原因是, 根部固定于定子壳体上, 叶片由根部到前缘逐渐远离壳体, 所受约束变小, 所以变形逐渐增大。

	Figure Option View Download New Window
	图4 流固耦合定子位移分布Fig.4 Deformation distribution for stator under FSI

图5为热流固耦合定子位移分布情况。由图可知, 在整体上, 位移分布情况与流固耦合大体一致, 但位移变形明显增大, 厚叶片也存在一定程度变形, 其位移大小相当于流固耦合最大值。另外, 不可压缩黏性油液冲击叶片表面, 产生大量热, 因叶片不同部位速度梯度差异, 叶片的温度不均匀, 使得叶片有不同程度的热膨胀, 以致叶片位移变形弯曲显著增大。在局部叶片上, 叶片前缘中心处位移最大达0.53 mm, 较流固耦合增大6%。分析其原因是:为便于油液循环流动, 在叶片前缘设置了30° 楔角, 致使前缘变薄, 力学性能变差, 更易受温度场影响。由此可知, 温度对位移变形有一定影响, 对液力缓速器叶片强度分析时有必要考虑温度因素。

	Figure Option View Download New Window
	图5 热流固耦合定子位移分布Fig.5 Deformation distribution for stator under TFSI

3.1.2 叶片位移随时间的变化

如图6所示, FSI和TFSI条件下叶片位移分布在各采样时间点都符合一般规律, 即沿叶片径向由根部到前缘呈圆弧状梯度增大, 在叶片压力面前缘中心处位移增至最大; 随着时间推进, 叶片整体位移逐渐增大。其主要原因是根部固定于壳体上, 而前缘为自由端, 并设有楔角, 厚度较薄, 致使叶片前缘中心处沿油液流动方向翘曲。如图6所示, 吸力面根部受压, 前缘中心处受拉, 而压力面受力状态相反; 随高速油液不断冲击叶片, 作用叶片表面的压力不断变大, 使位移区间不断扩大。

	Figure Option View Download New Window
	图6 定子叶片位移随时间变化分布Fig.6 Changes of deformation for stator blade with time under FSI and TFSI

为作进一步分析, 不失一般性地取叶片上位移最大点为采样点, 拟合绘制如图7所示的定子叶片最大位移点位移随时间变化的趋势线。在FSI条件下, 采样点位移较小, 位移与时间趋势线呈线性相关; 在TFSI条件下, 相同时间点的采样点位移明显增大, 位移与时间趋势线呈曲线相关。出现这种差异的主要原因是加载温度场后, 叶片发生了各向同性瞬时热膨胀; 另外, FSI变形是在屈服极限内, 材料力学属性占优, 而TFSI变形已超出了屈服极限, 变形过程中热膨胀逐渐占优, 致使位移与时间趋势线整体上呈曲线相关。这表明液力缓速器内温升过大, 产生的热膨胀变形也相应变大, 不利于缓速器长久持效工作, 因此必须对油液进行降温。

	Figure Option View Download New Window
	图7 定子叶片采样点位移随时间变化趋势Fig.7 Changes of deformation for sample point in stator with time

3.2 等效应力对比分析

3.2.1 整体等效应力计算结果

图8为流固耦合定子等效应力的分布情况。在整体上, 薄叶片在吸力面前缘与根部相交的两处显现局部高等效应力区, 而叶片中部呈低等效压力区, 厚叶片上的等效压力不明显。在局部叶片上, 等效应力在叶片表面上呈圆环状梯度减小, 在外环处最大, 大致为135 MPa, 外环集中应力区最大值可达269.87 MPa, 中部最小, 大致为75 MPa。这表明, 油液在冲击叶片表面过程中在叶片根部与定子壳体的刚性连接处附近产生应力集中, 使等效应力值偏大, 以致局部拐角处出现最大值, 前缘拐角处的应力值偏大也是由于产生应力集中造成。

	Figure Option View Download New Window
	图8 流固耦合定子等效应力分布Fig.8 Equivalent stress distribution for stator under FSI

图9为热流固耦合定子等效应力分布情况。整个定子的等效应力有所上升, 壳体上等效应力值比叶片上的大, 最大值出现在壳体内壁外环处, 最小值出现在叶片前缘中部。在局部叶片上, 叶片上的等效应力沿径向呈圆弧状梯度减小, 叶片根部与壳体内壁刚性连接处等效应力值较大, 最大等效应力值出现在前缘与根部相交拐角处, 大约468.14 MPa, 根部大约160 MPa, 内壁上大约100 MPa, 对应FSI最大应力位置下, 其值大约为326.13 MPa。由于叶片受热不均匀而存在着温度差异, 致使各处膨胀变形不一致, 热应力使整体等效应力增大, 其中最大等效应力值增大21%。这表明热应力对叶片等效应力值的影响较明显。

	Figure Option View Download New Window
	图9 热流固耦合定子等效应力分布Fig.9 Equivalent stress distribution for stator under TFSI

3.2.2 叶片等效应力随时间的变化

图10为定子叶片等效应力随时间的变化分布, 在FSI条件下, 等效应力在叶片表面根部及前缘处为应力集中区, 在进出口处, 应力集中更大, 而在中部呈峨眉月形低应力区; 在TFSI条件下, 等效应力在叶片根部固定端为应力集中区, 在进出口处应力值达到最大, 进出口之外呈弦月形低应力区。分析其原因可知, 由于流道叶片表面压力的分布, 导致加载到壳体叶片上的压力沿叶片径向圆弧状梯度减小; 另外, 由于叶片根部固定于壳体上, 而前缘为自由端, 受叶片倾角影响, 易在根部形成应力集中。

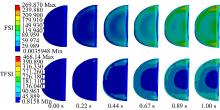	Figure Option View Download New Window
	图10 定子叶片等效应力随时间变化分布Fig.10 Changes of equivalent stress for stator blade with time under FSI and TFSI

由图10可以看出, 在叶片根部与前缘相交处的等效应力值最大, 形成危险点, 取叶片上危险点为采样点, 拟合绘制如图11所示的定子叶片危险点等效应力随时间变化的趋势线。在FSI条件下, 危险点处等效应力值较小, 等效应力与时间趋势线呈线性相关; 在TFSI条件下, 相同时间点时, 危险点等效应力增大, 且等效应力与时间趋势线呈曲性相关。存在这种变化的主要原因是由于加载温度后, 一方面叶片因温度的变化会发生热膨胀变形; 另一方面, 叶片上各处受热不均匀而存在着温度差异, 形成温度场, 导致各处膨胀变形不一致, 相互约束而产生热应力, 使得同时刻点的等效应力值变大, 与时间的趋势线整体上也呈曲线相关。

	Figure Option View Download New Window
	图11 定子叶片采样点等效应力随时间变化趋势Fig.11 Changes of equivalent stress for sample point in stator with time

4 结论

(1)通过对比流固耦合与热流固耦合分析方法发现, 液力缓速器在高速制动时产生的大量热在叶片表面形成温度场, 使叶片的位移及等效应力显著增大。因此, 采用热流固耦合对液力缓速器叶片强度进行分析预测更为准确、真实。

(2)本文中液力缓速器所选用的材料为铸铝104, 强度极限为490 MPa, 屈服极限为350 MPa, 由流固耦合分析得到最大等效应力值为269.87 MPa, 液力缓速器可以安全工作, 而采用热流固耦合强度分析表明, 定子叶片在外环根部局部点的等效应力最大值为326.13 MPa, 已逼近该选用材料的屈服极限, 存在安全隐患。故应当采用强度更高的其他材料, 例如, 铸钢、镁合金等, 或者在不影响制动效果基础上适量加厚叶片。

(3)与流固耦合对比, 本文的方法不仅避免了繁复冗长的操作, 而且通过ANSYS Workbench将压力场与温度场直接加载, 误差累积小, 计算值更为精准。另外, 在网格划分时考虑了油液黏性作用, 在流道与壁面的边界采用了棱柱网格。这些都使得该方法能更真实地模拟构件传力, 更好地掌握结构位移变形和应力分布。

(4)由分析结果可以看出, 液力缓速器叶片最大等效应力通常出现在叶片与外环的刚性连接处, 特别是叶片前缘拐角处, 应力集中十分明显, 易发生疲劳破坏。这与以往的叶片强度分析所得出的结论相一致^[2]。因此, 在进行液力缓速器结构设计时, 有必要在工作叶轮与外环壳体交接处采用圆弧过渡, 以提高叶片根部的抗疲劳强度, 缓解应力集中现象。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	吴超, 徐鸣, 李慧渊, 等. 车辆液力缓速器的特点分析及发展趋势[J]. 车辆与传动技术, 2011(1): 51-55. Wu Chao, Xu Ming, Li Hui-yuan, et al. Analysis of characteristic and development of vehicle hydraulic retarder[J]. Vehicle & Power Technology, 2011(1): 51-55. [本文引用:1]
[2]	过学迅, 梁荣亮, 陈见. 基于ANSYS的车辆液力缓速器叶片强度分析及模态分析[J]. 武汉理工大学学报: 交通科学与工程版, 2010, 34(1): 68-71. Guo Xue-xun, Liang Rong-liang, Chen Jian. Strength analysis and modal analysis of hydraulic retarder blade based on ANSYS[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2010, 34(1): 68-71. [本文引用:3]
[3]	王峰, 闫清东, 王书灵. 基于CFD和FEA的液力减速器叶片强度分析[J]. 北京理工大学学报: 自然科学版, 2006, 26(12): 1052-1060. Wang Feng, Yan Qing-dong, Wang Shu-ling. Strength analysis of hydraulic retarder rotator blades based on CFD and FEA[J]. Transactions of Beijing Institute of Technology (Natural Science Edition), 2006, 26(12): 1052-1060. [本文引用:1]
[4]	杨涛. 液力缓速器流场仿真及有限元分析[D]. 武汉: 武汉理工大学汽车工程学院, 2009. Yang Tao. Flow field simulation and finite element analysis of hydraulic retarder[D]. Wuhan: School of Automotive Engineering, Wuhan University of Technology, 2009. [本文引用:1]
[5]	Flomenhoft H I. Aeroelasticity and dynamic loads—from1903 to the supersonic era[C]∥AIAA Paper, 2000-1597. [本文引用:1]
[6]	Steinthorson E, Ameri A A, Rigby L D. Simulation of turbine cooling flows using multiblock—multigrid scheme[C]∥AIAA Paper, 96-0621. [本文引用:1]
[7]	York W D, Leylek J H. Three-dimensional conjugate heat transfer simulation of an internally-cooled gas turbine vane[C]∥Proceedings of ASME Turbo Expo2003, Atlanta, 2003: GT2003-38551. [本文引用:1]
[8]	Takahashi T, Watanabe K, Takahashi T. Thermal conjugate analysis of a first stage blade in a gas turbine[C]∥Proceedings of ASME Turbo Expo2000, Munich, 2000: 2000-GT-0251. [本文引用:1]
[9]	Nowak G, Wróblewski W, Chmielniak T. Optimization of cooling passages within a turbine vane[C]∥Proceedings of ASME Turbo Expo2005, Reno, 2005: GT2005-68552. [本文引用:1]
[10]	Dennis B H, Egorov I N, Dulikravich G S, et al. Optimization of a large number of coolant passages located close to the surface of a turbine blade[C]∥Proceedings of ASME Turbo Expo2003, Atlanta, 2003: GT2003-38051. [本文引用:1]
[11]	袁哲, 马文星, 刘春宝, 等. 重型车开式液力减速器温度场分析[J]. 吉林大学学报: 工学版, 2013, 43(5): 1271-1275. Yuan Zhe, Ma Wen-xing, Liu Chun-bao, et al. Temperature field analysis of the open-type hydrodynamic retarder of heavy vehicle[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(5): 1271-1275. [本文引用:1]
[12]	袁哲. 重型车液力缓速器热流耦合与散热系统研究[D]. 长春: 吉林大学机械科学与工程学院, 2013. Yuan Zhe. Study on heat-flow coupling and heat transfer system of hydrodynamic retarder of heavy vehicle[D]. Changchun: College of Mechanical Science and Engineering, Jilin University, 2013. [本文引用:1]

2011

0.0

. 2011, (1):51-55 DOI:doi:10.3969/j.issn.1009-4687.2011.01.011

Analysis of characteristic and development of vehicle hydraulic retarder

车辆液力缓速器的特点分析及发展趋势

Wu Chao , Xu Ming , Li Hui-yuan

吴超, 徐鸣, 李慧渊

首先概述了车辆液力缓速器的应用现状和工作原理,然后按照液力缓速器的不同类型,对其结构和技特点进行了重点分析,并结合实际应用提出了液力缓速器低空损和智能控制技术的发展趋势.

... 0 引言液力缓速器具有高速制动力矩大、制动平稳、噪声小、寿命长、体积较小等优点,在军用车辆、重型载货车以及工程机械等领域得到了广泛应用^[1] ...

2010

0.0

. 2010, 34(1):68-71 DOI:doi:10.3963/j.issn.1006-2823.2010.01.017

Strength analysis and modal analysis of hydraulic retarder blade based on ANSYS

基于ANSYS的车辆液力缓速器叶片强度分析及模态分析

Guo Xue-xun , Liang Rong-liang , Chen Jian

过学迅, 梁荣亮, 陈见

基于UG-NX2造型软件平台建立YJ-400型号液力缓速器三维几何模型,并对液力缓速器进行叶片的提取简化,利用ANSYS-UG的数据接口将叶片导入ANSYS生成FEA模型,利用计算流体分析软件Fluent对液力缓速器的内流场进行数值模拟.得到叶片表面的液压载荷分布,利用ANSYS的载荷施加模块将工作液液体总压按线性分布施加于FFA模型,进行叶片强度分析求得叶片的变形量和等效应力分布;同时对只施加有位移约束的FEA模型进行前六阶模态分析,求得各阶振型的固有频率和共振时叶片的最大变形量.

... 流固耦合的传统方法^[2,3,4]可总结为利用Matlab对Fluent求得的叶片表面的压力分布点进行坐标变换、曲面拟合,获取该叶片表面的液压载荷分布,再按线性分布加载到ANSYS生成的相应叶片FEA模型上进行叶片强度分析 ...

... 然而,应用此方法对有限元模型施加载荷时,以沿旋转半径方向的线性分布载荷模拟分布在叶片上的载荷,这未能真实体现出液体总压在叶片压力面上的分布,因为考虑到油液的黏性、油液与壁面的边界层处理和叶片非压力面的背压等因素的影响,叶片上的压力分布是无规律可循的^[2] ...

... 这与以往的叶片强度分析所得出的结论相一致^[2] ...

2006

0.0

. 2006, 26(12):1052-1060 DOI:doi:10.3969/j.issn.1001-0645.2006.12.005

Strength analysis of hydraulic retarder rotator blades based on CFD and FEA

基于CFD和FEA的液力减速器叶片强度分析

Wang Feng , Yan Qing-dong , Wang Shu-ling

王峰, 闫清东, 王书灵

Based on CFD numeric simulation for hydraulic retarder inner flow field,the pressure distribution functions of the rotator blades surfaces are regressed by coordinate transformation and surface fitting.Through the APDL program,pressure loads are loaded on the FEA model according to the regressed pressure functions,which vary with the x-and y-coordinates in local coordinates.The FEA model is solved and the blades strength is analyzed more accurately.The results showed that the stress on the root of the rotator blades is much higher than the critical stress intensity of the material under the condition of maximum rotating speed.

基于对某型液力减速器内流场的CFD数值模拟,运用坐标变换、曲面拟合等方法,得到其叶片表面的压力随局部坐标x,y变化的二元函数.根据拟合的压力分布函数,应用编制的APDL程序,将分布载荷施加到利用有限元分析软件ANSYS建立的FEA模型,从而实现了对流体压力作用下的叶片强度问题较为精确的有限元分析.结果表明,在最高转速工况,叶片根部应力过大,存在安全隐患.

2009

0.0

. 2009, :- DOI:doi:10.7666/d.y1611490

Flow field simulation and finite element analysis of hydraulic retarder

液力缓速器流场仿真及有限元分析

Yang Tao

杨涛

液力缓速器是应用最广泛的一种车辆辅助制动装置，利用动轮旋转带动内部油液流动，然后冲击定轮叶片，靠油液反作用力产生制动力矩，使车辆减速。本文基于CFD和FEA平台，利用VB、CATIA、ICEM-CFD、FLUENT、MATLAB、ANSYS等专业软件，对满充液条件下的液力缓速器内流场进行了仿真分析，获得了工作腔内部油液的流动规律以及压力场和速度场的分布情况。并分析了液力缓速器动轮和定轮的强度和模态。基本上建立了一整套液力缓速器流场分析和有限元分析方法。这对自主研发生产液力缓速器的有一定的指导作用。　　论文介绍了液力缓速器在国内外的发展应用情况、优缺...

0.0

... 早期航空领域的气动弹性问题^[5],就是典型的流固耦合作用 ...

0.0

... 美国国家航空航天局的Lewis研究中心对气热弹耦合进行了探索^[6],主要研究了应用多块结构网格计算复杂几何三维黏性流场与涡轮冷却流动现象 ...

0.0

... York等^[7]利用耦合传热方法模拟了气轮机叶片在两种不同的发动机实际操作条件下的温度分布 ...

0.0

... Takahashi等^[8]采用数值模拟计算研究了由圆形表面光滑通道进行冷却的涡轮叶片的耦合传热问题 ...

0.0

... Nowak等^[9]基于热流固耦合,搜索C3X型叶片在冷却孔数目不变的情况下,优化最大热应力和最高温度较小的最佳冷却结构,优化后叶片的最高温度明显低于优化前,叶片的等效应力和温度场分布均有一定的改善 ...

0.0

... Dennis等^[10]利用约束优化方法对某直叶片进行了改善,使得叶片表面温度分布更加均匀,并且较大幅度地降低了热传导量 ...

2013

0.0

. 2013, 43(5):1271-1275 DOI:doi:10.7964/jdxbgxb201305020

Temperature field analysis of the open-type hydrodynamic retarder of heavy vehicle

重型车开式液力减速器温度场分析

Yuan Zhe , Ma Wen-xing , Liu Chun-bao

袁哲, 马文星, 刘春宝

Computational Fluid Dynamics (CFD) method is employed to compute the temperature field of open-type hydrodynamic retarder with an effective diameter of 468 mm. By simulation and analysis, the relationship between temperature and rotating speed of the hydrodynamic retarder in the condition of full filled liquid is obtained. The internal temperature field of the hydrodynamic retarder is analyzed. On that basis, the open-type hydrodynamic retarder under the conditions of the same rotating speed and different liquid filling rates are computed. The relationship between temperature and liquid filling rate is obtained. Through simulating, it provides an important theoretical basis for the heat exchange of open-type hydrodynamic retarder at different gears.

采用计算流体动力学(CFD)方法,对循环圆直径为468 mm的开式液力减速器进行了温度场计算。经过仿真计算和分析,得到在全充液工况下液力减速器温度与转子转速的关系曲线,并对其内部温度场进行了分析。在此基础上,对开式液力减速器在相同转速、不同充液率的工况下进行了数值计算,得到温度与充液率关系曲线。通过仿真分析,为开式液力减速器在各个档位制动时的热交换问题提供了重要的理论依据。

... (1)在流场域内进行流道的数值计算,假定流体不可压,则流动流体所需满足的方程理论有^[11]: ...

2013

0.0

. 2013, :-

Study on heat-flow coupling and heat transfer system of hydrodynamic retarder of heavy vehicle

重型车液力缓速器热流耦合与散热系统研究

Yuan Zhe

袁哲

近些年来，运输的高速化和重型化对车辆的制动性能提出了更高的要求。传统的行车制动器已经不能满足长时间频繁制动的需要，重型车急需装备一种辅助制动系统。液力缓速器具备了制动平稳、高速制动能力强、体积小及噪声小等优点，因此在这一领域获得了广泛应用。液力缓速器通过作用于传动系统而减轻车辆制动系统的负荷，使车辆均匀减速，提高了车辆制动系统的可靠性和安全性。通过减少车辆行驶中的制动次数，延长了制动器和轮胎的使用寿命，体现出液力缓速器具有较高的经济性。通过减少频繁的启、制动，安装了液力缓速器的车辆可提高乘客的舒适性。但液力缓速器在工作过程中，油温会不断升高，如果冷却系统不能达到很好的散热效果，产生的热量不能被及时释放，就可能导致工作油变质、部分机件损坏、密封件失效漏油等，这些都会导致缓速器制动性能下降和行车制动器可靠性降低。本文以杭州前进齿轮箱集团股份有限公司“重型及特种车辆自动变速技术研究(7-2010-008)”为依托，针对液力缓速器工作腔内部及板翅式换热器内部的流体流动与换热特性进行了CFD数值计算和试验研究。主要研究内容有如下几方面： 1.液力缓速器的热流耦合研究基于热流耦合的数值模拟理论，以R295型闭式液力缓速器与D438型开式液力缓速器作为研究对象，对其在不同转速和不同充液率工况进行了流动传热的数值计算。通过对转子转速为1500r/min，液力缓速器工作腔内温度场及流场分布趋势的分析、研究，了解了液力缓速器在全充液和部分充液工况下的内部流动规律与温度场情况。通过对工作腔内流动特性及温度场规律形成原因的深入分析，对液力缓速器的工作机理有了更加全面、透彻的了解，进而便于对液力缓速器进行优化设计。接着，在忽略温度对工作油物理性质影响的情况下，对R295型闭式液力缓速器与D438型开式液力缓速器，在不同转速且全充液工况下的制动转矩进行了数值计算，得到二者的制动转矩与转速关系曲线。在此基础上，以相同制动转矩为基点，对经过循环圆相似放大的481mm开式液力缓速器与循环圆直径仍为295mm的闭式液力缓速器在不同转速且全充液、相同转速且不同充液率的工况分别进行了数值计算，得到二者的制动转矩与转速、制动转矩与充液率关系曲线。通过开式与闭式液力缓速器的对比分析，进一步了解了两种类型液力缓速器各自的优点和不足，为重型车液力缓速器的选型提供了一定的理论依据，也为换热器的选型提供了前提条件。 2.液力缓速器的换热器数值分析通过对开式与闭式液力缓速器温度对比，得知闭式液力缓速器的温度较高，因此重点介绍了为R295型闭式液力缓速器进行的换热器选型。首先，对为R295型闭式液力缓速器选择的板翅式换热器的冷却性能进行了分析。为板翅式换热器的芯体选择平直型和锯齿型两种不同的翅片类型，由于计算条件有限，对两种翅片类型的换热器模型进行了简化，选取周期模型作为计算区域。在进行边界条件与相关参数设置后，对两种不同翅片类型的板翅式换热器进行了CFD数值计算。数值计算结果表明，锯齿型翅片换热器的散热效果要好于平直型翅片换热器，平直型翅片的板翅式换热器不能满足R295型闭式液力缓速器对散热的需求，但锯齿型翅片则满足要求。通过对选择的锯齿型板翅式换热器的压降核算，证明其压降值在合理的范围内，符合使用要求。在此基础上，研究了锯齿型板翅式换热器的工作油进口速度对温度分布的影响，得知随着工作油进口速度的增加，工作油的质量流量也随之增加，沿流动方向的温度降低速度较慢。 3.工作油温度对制动性能影响的研究由于不同温度下，液力缓速器内的液力传动油具有不同的物理性质，会对液力缓速器的制动性能造成一定影响。因此，对工作油温度对液力缓速器制动性能的影响进行了分析。首先对液力缓速器内工作油温度随工况及充液率的变化规律进行研究，得知随着转速的增加，工作腔内工作油温度升高；在相同转速下，随着充液率的增加，工作油的温度也随之升高。在此基础上，在考虑温度对工作油物理性质影响的条件下，研究了不同工况与不同充液率下液力缓速器的制动特性。通过分析，得知随着转速的增加，液力缓速器的制动转矩变大，油温升高，与忽略油温影响的情况相比较，制动性能变差；而在转速相同的情况下，随着充液率的增加，液力缓速器制动转矩值增大，工作油温度随之升高，与忽略油温影响的情况相比较，制动性能仍然变差。 4.液力缓速器热平衡试验研究对循环圆直径为438mm的开式液力缓速器进行了热平衡试验研究。通过台架试验，测量得到在不同转速且全充液工况下的开式液力缓速器进油口与出油口处工作油的温度。将通过台架试验测量的液力缓速器出口油温与CFD数值计算所得结果进行对比，二者所得结果基本吻合，也由此证明了利用流动传热计算方法的正确性和可靠性。

... s)^[12] ...