数控机床可靠性评估试验周期设计

引用本文

李洪洲, 杨兆军, 许彬彬, 王彦鹍, 贾玉辉, 侯超. 数控机床可靠性评估试验周期设计. 2016, 46(5): 1520-1527
LI Hong-zhou, YANG Zhao-jun, XU Bin-bin, WANG Yan-kun, JIA Yu-hui, HOU Chao. Design of testing period for reliability assessment of NC machine tools. Journal of Jilin University Engineering and Technology Edition, 2016, 46(5): 1520-1527 复制到剪切板

Permissions

数控机床可靠性评估试验周期设计

李洪洲^1,², 杨兆军¹, 许彬彬¹, 王彦鹍¹, 贾玉辉¹, 侯超¹

1.吉林大学机械科学与工程学院,长春 130022

2.北华大学机械工程学院,吉林省吉林市 132011

通信作者:杨兆军(1956-),男,教授,博士生导师.研究方向:数控装备可靠性理论.E-mail:yzj@jlu.edu.cn

作者简介:李洪洲(1974-),男,副教授,博士研究生.研究方向:数控机床可靠性.E-mail:yinshun_9999@163.com

基金:国家科技重大专项项目(2013ZX04011-012).

摘要

针对数控机床可靠性评估试验时由于试验周期难以确定而造成的试验成本升高或评估精度降低的问题,提出了一种基于Bootstrap重抽样的试验周期设计方法。该方法以平均故障间隔工作时间(MTBF)的区间估计变化率作为判定试验周期长度的依据,以Bootstrap重抽样方法求解数控机床MTBF的区间估计,以Power函数建立了MTBF区间估计变化率模型,得到了可靠性评估试验的试验周期。结合实例分析了机床台数m和形状参数β对试验周期的影响:随着形状参数β或被试机床台数m的增加,可靠性评估试验的试验周期缩短。

关键词: 数控机床; Bootstrap; 试验周期; 区间估计

中图分类号:TG659 文献标志码:A 文章编号:1671-5497(2016)05-1520-08

Design of testing period for reliability assessment of NC machine tools

LI Hong-zhou^1,², YANG Zhao-jun¹, XU Bin-bin¹, WANG Yan-kun¹, JIA Yu-hui¹, HOU Chao¹

1.College of Mechanical Science and Engineering,Jilin University,Changchun 130022,China

2.College of Mechanical Engineering,Beihua University,Jilin 132011,China

Abstract

To overcome the problem that the difficulty in determining the testing period for reliability assessment of NC machine tools increases the testing cost or decreases the assessment accuracy, a new method to determine the testing period is proposed based on Bootstrap re-sampling. This method uses the change rate of interval estimate of Mean Time between Failures (MTBF) as the basis for determining the testing period, and then calculates the interval estimate of MTBF using Bootstrap re-sampling. The model of change rate for interval estimate of MTBF is established by power function, and the testing period for the reliability assessment of NC machine tools is obtained. Two factors influencing the testing period, the number of machine tools and shape parameter, are analyzed in combination with the real case. Results indicate that with increase in the shape parameter and the number of tools, the testing period of reliability assessment is shortened.

Keyword: NC machine tools; Bootstrap; testing period; interval estimation

Show Figures

0 引言

现场可靠性试验是进行数控机床可靠性评估的基本方法, 也是数控机床故障分析和可靠性改进设计的主要数据来源^{[1, 2]}。为了使可靠性评估结果更加准确, 现场可靠性试验往往需要设定较长的试验周期, 这会使试验成本上升。为了降低试验成本, 就要缩短试验周期, 这又会导致评估精度降低。因此, 在保证可靠性评估精度的前提下使可靠性试验周期最短, 并确定两者之间的量化关系, 具有重要工程意义。余闯等^[3]和陈炳锟^[4]在综合考虑生产方风险和使用方风险的前提下提出产品交付使用时进行序贯试验的试验件数及试验时间的确定方法。Mckane等^[5]研究了被试产品服从对数位置-尺度模型时, 在不同枢轴量区间估计宽度的要求下确定试验件数和试验时间的试验方案。何峻等^[6]以评估参数的区间估计长度最短作为判断依据来确定试验样本量。Guo等^[7]提出以上、下区间估计长度的对数比为评估精度要求来确定可靠性样本试验周期的方法。由此可知上述文献多以模型参数的区间估计精度作为确定试验周期和样本量的依据。对于数控机床, 其故障间隔工作时间通常服从威布尔分布^{[8, 9, 10]}, 而上述文献方法均不适用于威布尔分布, 不宜直接应用于数控机床的可靠性评估的试验周期的确定。因此, 如何科学合理地确定数控机床可靠性评估的试验周期需要作进一步深入的探讨。

借鉴上述文献, 本文以平均故障间隔工作时间的区间估计宽度的变化率作为确定试验周期的依据。其物理意义为:可靠性评估试验在进行一个单位时间的试验时, 平均故障间隔工作时间的区间估计宽度的变化量。在结合相似数控机床历史故障数据的基础上, 应用Bootstrap方法求取MTBF的区间估计及其变化率, 给出了可靠性评估的试验周期设计模型。结合实例验证了该方法的可行性。

1 数控机床可靠性的区间估计

1.1 数控机床可靠性模型

许多学者已证明数控机床故障间隔时间服从二参数威布尔分布^{[8, 9, 10]}, 其可靠度函数为:

$\begin{matrix} R (t) = \exp [- {(\frac{t}{η})}^{β}], t \geq 0 (1) \end{matrix}$

故障概率密度函数为:

$\begin{matrix} f (t) = β η^{- β} t^{β - 1} \exp [- {(\frac{t}{η})}^{β}], t \geq 0 (2) \end{matrix}$

式中: $\begin{matrix} β \end{matrix}$ 为形状参数; $\begin{matrix} η \end{matrix}$ 为尺度参数。

数控机床平均故障间隔工作时间(MTBF)为:

$\begin{matrix} MTBF = η \times Γ (1 + 1 / β) (3) \end{matrix}$

式中: $\begin{matrix} Γ \end{matrix}$ 为Gamma函数。

1.2 模型参数的点估计

通常数控机床可靠性评估试验为多台机床定时截尾试验, 设有 $m$ 台数控机床进行定时截尾试验, $t_{ij}$ 为第 $i$ 台被试数控机床从发生第 $j - 1$ 次故障到发生第j次故障的故障间隔工作时间, $T_{ij}$ 为第 $i$ 台被试数控机床发生第j次故障的时刻, $T$ 为该批数控机床试验周期。设 $t_{i}$ 为第 $i$ 台数控机床的定时截尾数据, $t_{i} = T - T_{i n_{i}}, n_{i}$ 表示第 $\begin{matrix} i \end{matrix}$ 台数控机床发生故障的次数。

定时截尾试验场合下的似然函数为:

$\begin{matrix} \begin{matrix} L (η, β) = \overset{m}{\prod_{i = 1}} \overset{n_{i}}{\prod_{j = 1}} f (t_{ij}) \times \overset{m}{\prod_{i = 1}} R (t_{i}) = \\ \overset{m}{\prod_{i = 1}} \overset{n_{i}}{\prod_{j = 1}} \{β η^{- β} {t_{ij}}^{β - 1} \exp [- {(\frac{t_{ij}}{η})}^{β}]\} \times \\ \overset{m}{\prod_{i = 1}} \exp [- {(\frac{t_{i}}{η})}^{β}] (4) \end{matrix} \end{matrix}$

对式(4)取对数得到:

$\begin{matrix} \begin{matrix} lnL (η, β) = lnβ \times \overset{m}{\sum_{i = 1}} n_{i} - lnη \times \overset{m}{\sum_{i = 1}} n_{i} β + \\ (β - 1) \times \overset{m}{\sum_{i = 1}} \ln (t_{i 1} t_{i 2} \dots t_{i n_{i}}) - \\ \overset{m}{\sum_{i = 1}} \overset{n_{i}}{\sum_{j = 1}} {(\frac{t_{ij}}{η})}^{β} - \overset{m}{\sum_{i = 1}} {(\frac{t_{i}}{η})}^{β} (5) \end{matrix} \end{matrix}$

式(5)无解析解, 本文采用模拟退火优化算法^[11]求解式(5)中的形状参数 $β$ 和尺度参数 $\begin{matrix} η \end{matrix}$ 的点估计。

1.3 模型参数的区间估计

本文采用参数Bootstrap方法进行可靠性参数的区间估计。该方法通过重抽样来构造Bootstrap样本, 常用于计算样本参数的区间估计^{[12, 13]}。数控机床可靠性参数的区间估计步骤如图1所示。

	Figure Option View Download New Window
	图1 数控机床可靠性参数Bootstrap区间估计流程Fig.1 Bootstrap interval estimation of reliability parameters for NC machine tools

在给定置信水平 $γ$ 下, 由图1可求解出 $m$ 台数控机床在试验周期 $\begin{matrix} T \end{matrix}$ 时MTBF的区间估计为 $[MTB F_{(B \cdot (γ / 2))}, MTB F_{(B \cdot (1 - γ / 2))}];$ 形状参数 $\begin{matrix} β \end{matrix}$ 的区间估计为 $[β_{(B \cdot (γ / 2))}, β_{(B \cdot (1 - γ / 2))}]$ ; 尺度参数 $\begin{matrix} η \end{matrix}$ 的区间估计为 $\begin{matrix} [η_{(B \cdot (γ / 2))}, η_{(B \cdot (1 - γ / 2))}] 。 \end{matrix}$

2 试验周期的确定

在Bootstrap重抽样时, 可设定 $k$ 个不同的试验周期T。分别求解在每个试验周期 $\begin{matrix} T \end{matrix}$ 时参数MTBF、η 、β 的区间估计值: $[MTB F_{(B \cdot (γ / 2))}^{1}, MTB F_{(B \cdot (1 - γ / 2))}^{1}], [MTB F_{(B \cdot (γ / 2))}^{2}, MTB F_{(B \cdot (1 - γ / 2))}^{2}], \dots$ , $[MTB F_{(B \cdot (γ / 2))}^{k}, MTB F_{(B \cdot (1 - γ / 2))}^{k}]; [β_{(B \cdot (γ / 2))}^{1}, β_{(B \cdot (1 - γ / 2))}^{1}], [β_{(B \cdot (γ / 2))}^{2}, β_{(B \cdot (1 - γ / 2))}^{2}], \dots$ , $[β_{(B \cdot (γ / 2))}^{k}, β_{(B \cdot (1 - γ / 2))}^{k}]; [η_{(B \cdot (γ / 2))}^{1}, η_{(B \cdot (1 - γ / 2))}^{1}], [η_{(B \cdot (γ / 2))}^{2}, η_{(B \cdot (1 - γ / 2))}^{2}], \dots, [η_{(B \cdot (γ / 2))}^{k}, η_{(B \cdot (1 - γ / 2))}^{k}]$ 。

对 $\begin{matrix} k \end{matrix}$ 个MTBF区间上限值 $\begin{matrix} MTB F_{(B \cdot (1 - γ / 2))}^{1}, MTB F_{(B \cdot (1 - γ / 2))}^{2}, \dots, MTB F_{(B \cdot (1 - γ / 2))}^{k} \end{matrix}$ 采用Matlab Cftool工具箱进行函数拟合, 得到MTBF区间估计的上限值拟合函数 $\begin{matrix} H_{up}^{MTBF} (T) 。 \end{matrix}$

同理可分别得到 $\begin{matrix} η 、 β \end{matrix}$ 区间估计的上限值拟合函数 $\begin{matrix} H_{up}^{η} (T), H_{up}^{β} (T) 。 \end{matrix}$

对 $\begin{matrix} k \end{matrix}$ 个MTBF区间下限值 $\begin{matrix} MTB F_{(B \cdot (γ / 2))}^{1}, MTB F_{(B \cdot (γ / 2))}^{2}, \dots, MTB F_{(B \cdot (γ / 2))}^{k} \end{matrix}$ 采用Matlab Cftool工具箱进行函数拟合, 得到MTBF区间估计的下限值拟合函数 $\begin{matrix} H_{Low}^{MTBF} (T) 。 \end{matrix}$

同理可分别得到 $\begin{matrix} η 、 β \end{matrix}$ 区间估计的下限值拟合函数 $\begin{matrix} H_{Low}^{η} (T), H_{Low}^{β} (T) 。 \end{matrix}$

为表达方便, $\begin{matrix} H_{up}^{MTBF} (T) 、 H_{up}^{η} (T) 、 H_{up}^{β} (T) \end{matrix}$ 统一表示为 $\begin{matrix} H_{up} (T) 。 H_{Low}^{MTBF} (T) 、 H_{Low}^{η} (T) 、 H_{Low}^{β} (T) \end{matrix}$ 统一表示为 $\begin{matrix} H_{Low} (T), \end{matrix}$ 则MTBF、 $\begin{matrix} η 、 β \end{matrix}$ 区间估计宽度为:

$\begin{matrix} F (T) = H_{up} (T) - H_{Low} (T) (6) \end{matrix}$

对式(6)求导数分别得到MTBF、 $\begin{matrix} η 、 β \end{matrix}$ 的区间估计变化率为:

$\begin{matrix} Q (T) = \frac{\partial F_{} (T)}{\partial T} = \frac{\partial H_{up} (T)}{\partial T} - \frac{\partial H_{Low} (T)}{\partial T} (7) \end{matrix}$

文献[5, 6, 7]以参数的区间估计的宽度或上、下区间比作为评估要求。本文以MTBF、 $η 、 β$ 区间估计宽度的变化率 $\begin{matrix} Q (T) \end{matrix}$ 作为可靠性评估试验要求。设Q_MTBF为可靠性评估试验时要求达到的MTBF区间估计宽度的变化率。则机床试验周期 $\begin{matrix} T \end{matrix}$ 应满足:

$\begin{matrix} |Q (T)| = |\frac{\partial F (T)}{\partial T}| \leq Q_{MTBF} (8) \end{matrix}$

设 $Q_{η}$ 为可靠性评估试验时要求达到的 $η$ 的区间估计变化率。则机床试验周期 $\begin{matrix} T \end{matrix}$ 应满足:

$\begin{matrix} |Q (T)| = |\frac{\partial F (T)}{\partial T}| \leq Q_{η} (9) \end{matrix}$

设 $Q_{β}$ 为可靠性评估试验时要求达到的 $β$ 的区间估计变化率。则机床试验周期 $\begin{matrix} T \end{matrix}$ 应满足:

$\begin{matrix} |Q (T)| = |\frac{\partial F (T)}{\partial T}| \leq Q_{β} (10) \end{matrix}$

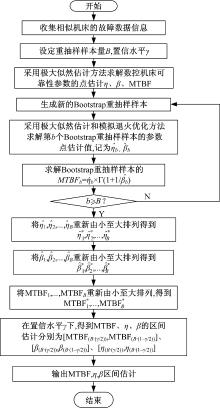
由式(4)~(10)可以看出, 影响机床试验周期 $T$ 的参数为被试机床台数 $m$ 和形状参数 $\begin{matrix} β 。 \end{matrix}$

3 实例分析

课题组将对11台某型号的加工中心进行可靠性评估试验, 试验方法为用户现场的定时截尾试验。试验前, 首先要确定试验周期T。要求确定可靠性评估试验周期T是以MTBF的区间宽度变化率为指标, 设:Q_MTBF=0.2。则具体步骤为:

(1)确定该批机床的可靠性模型参数

在试验前, 收集了与该型号机床相似的机床的历史故障数据信息, 故障间隔工作时间分别为:386, 248, 874, 83, 214, 1623, 934, 91, 1546, 204, 1685 h。通常数控机床故障间隔工作时间服从威布尔分布, 则通过1.1节和1.2节求得模型参数为:η =740.8671, β =1.0886。根据式(3)得MTBF=717.3649 h。

(2)MTBF的区间估计

根据1.3节Bootstrap区间估计方法, 设定试验周期T为1~6倍的MTBF。以0.1倍MTBF为步长进行Bootstrap重抽样, 则分别得到各Bootstrap重抽样试验周期T处的MTBF的区间估计上、下限值, 以Matlab Cftool工具箱中的Power函数对区间估计的上、下限值分别进行拟合。得到MTBF的区间估计上限拟合函数为:

$\begin{matrix} H_{up} (T) = 1.6410 T^{- 1.9860} + 1.2500 \end{matrix}$

MTBF的区间估计下限拟合函数为:

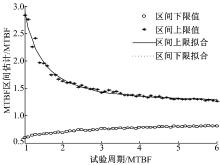
$\begin{matrix} H_{Low} (T) = - 0.3904 T^{- 0.4468} + 0.9885 \end{matrix}$

则拟合结果如图2所示。

	Figure Option View Download New Window
	图2 MTBF区间估计拟合Fig.2 Interval estimation fitting of MTBF

由图2可知, 该批机床的MTBF区间估计随试验周期T的延长而急剧变短, 达到一定试验时间后趋于稳定。

由式(7)得到MTBF的区间估计变化率函数:

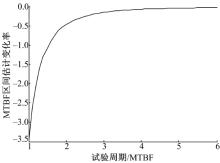
$\begin{matrix} \begin{matrix} Q (T) = 1.6410 \times (- 1.9860) T^{(- 1.9860 - 1)} - \\ (- 0.3904) \times (- 0.4468) T^{(- 0.4468 - 1)} \end{matrix} \end{matrix}$

则拟合结果如图3及表1所示。

	Figure Option View Download New Window
	图3 MTBF区间估计变化率Fig.3 Change rate of interval estimation of MTBF

表1 MTBF区间估计变化率 Table 1 Change rate of interval estimation of MTBF

由图3和表1知:随试验周期T的延长, MTBF区间估计变化率 $\begin{matrix} | Q (T) | \end{matrix}$ 趋于零。根据试验前要求的MTBF区间估计变化率Q_MTBF=0.2, 可确定该批机床可靠性评估试验的试验周期为2.7467倍MTBF, 约为2.7467× 717.3649≈ 1970 h, 此时|Q(T)|=0.1999< Q_MTBF, 满足试验设定的要求。

3.1 机床试验台数m对试验周期T的影响

为了分析被试机床台数 $m$ 对机床可靠性评估试验的试验周期 $T$ 的影响, 本文假设该型号被试机床有很多台, 如30台, 并仍服从参数为 $\begin{matrix} η = 740.8671 、 β = 1.0886 \end{matrix}$ 的威布尔分布。可靠性评估试验要求不变, 即:MTBF区间估计变化率Q_MTBF=0.2。

依次改变试验周期T, 采用1.3节区间估计方法可分别得到被试机床台数为1、2、3、4、5、11、20、30台时MTBF区间估计的上限值和下限值, 如图4所示。

	Figure Option View Download New Window
	图4 不同机床台数时MTBF区间估计值Fig.4 Interval estimation of MTBF under different NC machine tools number

由图4可知, 当只有1台被试机床时, 随着试验周期T的延长, MTBF区间估计呈无规律波动, 此时, 不能根据区间估计的变化率来确定试验周期T, 产生该现象的主要原因为:产生的故障数据较少, 属于小样本数据。当被试机床台数大于、等于2台时, 随着被试机床试验周期T的延长, MTBF的区间估计宽度呈规律性变化。

对上述大于、等于2台机床的MTBF区间估计上、下限值分别以Matlab Cftool工具箱中的Power函数进行拟合, 得到MTBF区间估计上限拟合函数H_up(T)和下限拟合函数H_Low(T), 如表2所示。

表2 不同台数机床时MTBF区间估计拟合函数 Table 2 Fitting function of MTBF interval estimation under different NC machine tools number

机床台数/台	区间估计上限拟合函数	区间估计下限拟合函数
2	$\begin{matrix} 7.0240 T^{- 0.8165} + 0.2183 \end{matrix}$	$\begin{matrix} - 0.9755 T^{- 0.1755} + 1.3530 \end{matrix}$
3	$\begin{matrix} 5.4990 T^{- 1.0380} + 0.7312 \end{matrix}$	$\begin{matrix} - 0.5677 T^{- 0.3294} + 0.9973 \end{matrix}$
4	$\begin{matrix} 4.5680 T^{- 1.2380} + 0.9618 \end{matrix}$	$\begin{matrix} - 0.5609 T^{- 0.3357} + 1.0250 \end{matrix}$
5	$\begin{matrix} 3.6020 T^{- 1.4310} + 1.1450 \end{matrix}$	$\begin{matrix} - 0.5529 T^{- 0.3315} + 1.0490 \end{matrix}$
11	$\begin{matrix} 1.6410 T^{- 1.9860} + 1.2500 \end{matrix}$	$\begin{matrix} - 0.3904 T^{- 0.4468} + 0.9885 \end{matrix}$
20	$\begin{matrix} 0.8404 T^{- 1.5420} + 1.1460 \end{matrix}$	$\begin{matrix} - 0.3054 T^{- 0.5603} + 0.9665 \end{matrix}$
30	$\begin{matrix} 0.5837 T^{- 1.4270} + 1.1130 \end{matrix}$	$\begin{matrix} - 0.2782 T^{- 0.4938} + 0.9934 \end{matrix}$

表2 不同台数机床时MTBF区间估计拟合函数 Table 2 Fitting function of MTBF interval estimation under different NC machine tools number

由式(7)及表2可得到不同台数机床的MTBF的区间估计变化率函数 $\begin{matrix} Q (T), \end{matrix}$ 如表3和图5所示。

表3 不同台数被试机床时MTBF的区间估计变化率函数 Table 3 Change rate of MTBF interval estimation under different NC machine tools number

机床台数/台	MTBF区间估计变化率函数
2	$\begin{matrix} 7.0240 \times (- 0.8165) T^{(- 0.8165 - 1)} + 0.9755 \times (- 0.1755) T^{(- 0.1755 - 1)} \end{matrix}$
3	$\begin{matrix} 5.4990 \times (- 1.0380) T^{(- 1.0380 - 1)} + 0.5677 \times (- 0.3294) T^{(- 0.3294 - 1)} \end{matrix}$
4	$\begin{matrix} 4.5680 \times (- 1.2380) T^{(- 1.2380 - 1)} + 0.5609 \times (- 0.3357) T^{(- 0.3357 - 1)} \end{matrix}$
5	$\begin{matrix} 3.6020 \times (- 1.4310) T^{(- 1.4310 - 1)} + 0.5529 \times (- 0.3315) T^{(- 0.3315 - 1)} \end{matrix}$
11	$\begin{matrix} 1.6410 \times (- 1.9860) T^{(- 1.9860 - 1)} + 0.3904 \times (- 0.4468) T^{(- 0.4468 - 1)} \end{matrix}$
20	$\begin{matrix} 0.8404 \times (- 1.5420) T^{(- 1.5420 - 1)} + 0.3054 \times (- 0.5603) T^{(- 0.5603 - 1)} \end{matrix}$
30	$\begin{matrix} 0.5837 \times (- 1.4270) T^{(- 1.4270 - 1)} + 0.2782 \times (- 0.4938) T^{(- 0.4938 - 1)} \end{matrix}$

表3 不同台数被试机床时MTBF的区间估计变化率函数 Table 3 Change rate of MTBF interval estimation under different NC machine tools number

	Figure Option View Download New Window
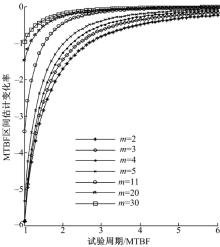	图5 不同台数被试机床时MTBF区间估计的变化率Fig.5 Change rate of MTBF interval estimation under different NC machine tools number

由图5可知, 在满足Q_MTBF=0.2的前提下, 不同台数被试机床的可靠性评估试验的试验周期 $\begin{matrix} T \end{matrix}$ 如表4所示。表4中第三列数值等于第二列数值乘以717.3649。

表4 不同台数被试机床的试验周期 Table 4 Testing periods under different NC machine tools number

由表4、图5可知, 当被试机床台数由2台增至5台时, 其可靠性评估试验的试验周期T可缩短最少(6-4.0545)× 717.3649≈ 1396 h。当被试机床台数由11台增至20台时, 其可靠性评估试验的试验周期T缩短了(2.7463-2.3133)× 717.3649≈ 311 h。而当被试机床台数由20台增至30台时, 其可靠性评估试验的试验周期T只缩短了(2.3133-2.0168)× 717.3649≈ 213 h。由此可以看出:随着被试机床台数 $\begin{matrix} m \end{matrix}$ 的增加, 机床可靠性评估的试验周期T缩短, 但当被试机床台数 $\begin{matrix} m \end{matrix}$ 达到一定数量时, 如20台, 该批机床可靠性评估试验的试验周期T缩短的幅度不大。因此, 在进行数控机床可靠性评估试验时, 应合理控制被试机床台数m。

3.2 形状参数β 对试验周期T的影响

在数控机床可靠性评估试验中, 威布尔分布的形状参数 $β$ 代表了数控机床所处的状态, 即当 $β < 1$ 时, 机床处于早期故障期; 当 $β = 1$ 时, 机床处于偶然故障期; 当 $\begin{matrix} β > 1 \end{matrix}$ 时, 机床处于耗损期。通常认为数控机床β 值落在[0.5, 3.0]范围内^{[4, 8, 9]}。因此, 仍以该型号机床为研究对象, 假设有处于不同 $β$ 值时的被试机床需要在试验前确定试验周期 $T$ 。为讨论方便, $\begin{matrix} β \end{matrix}$ 分别取值为0.5, 0.8, 1.0, 1.2, 1.5, 2.0, 3.0, 并假设尺度参数仍为η =740.8671, 试验机床台数仍为11台, 采用本文1.3节重抽样方法得到MTBF区间估计上、下限值, 如图6所示。试验前要求的MTBF区间估计变化率仍为Q_MTBF=0.2。在图6中, 为了比较不同 $\begin{matrix} β \end{matrix}$ 值对MTBF区间估计的影响, 对坐标进行归一化处理, 即坐标值除以不同形状参数 $\begin{matrix} β \end{matrix}$ 对应的MTBF。

	Figure Option View Download New Window
	图6 不同β 下的MTBF区间估计值Fig.6 Interval estimation of MTBF with different shape parameter β

对上述不同形状参数 $\begin{matrix} β \end{matrix}$ 下的数控机床MTBF区间估计上、下限值以Matlab Cftool工具箱中的Power函数分别进行拟合, 得到MTBF的区间估计上限拟合函数 $H_{up} (T)$ 和区间估计下限拟合函数 $\begin{matrix} H_{Low} (T), \end{matrix}$ 如表5所示。

表5 不同β 时MTBF区间估计拟合函数 Table 5 Fitting function of MTBF interval estimation with different shape parameter β

形状参数	区间估计上限拟合函数	区间估计下限拟合函数
0.5	$\begin{matrix} 3.8210 T^{- 0.8250} + 0.9184 \end{matrix}$	$\begin{matrix} - 0.9259 T^{- 0.1606} + 1.3560 \end{matrix}$
0.8	$\begin{matrix} 2.2980 T^{- 1.3710} + 1.2170 \end{matrix}$	$\begin{matrix} - 0.5181 T^{- 0.3334} + 1.0490 \end{matrix}$
1.0	$\begin{matrix} 1.8220 T^{- 1.8520} + 1.2680 \end{matrix}$	$\begin{matrix} - 0.4496 T^{- 0.3684} + 1.0330 \end{matrix}$
1.2	$\begin{matrix} 1.4390 T^{- 1.9450} + 1.2220 \end{matrix}$	$\begin{matrix} - 0.3696 T^{- 0.4489} + 0.9912 \end{matrix}$
1.5	$\begin{matrix} 1.1200 T^{- 2.4870} + 1.2070 \end{matrix}$	$\begin{matrix} - 0.2855 T^{- 0.6205} + 0.9478 \end{matrix}$
2.0	$\begin{matrix} 0.8590 T^{- 3.002} + 1.1630 \end{matrix}$	$\begin{matrix} - 0.2510 T^{- 0.6134} + 0.9675 \end{matrix}$
3.0	$\begin{matrix} 0.4916 T^{- 3.4350} + 1.1140 \end{matrix}$	$\begin{matrix} - 0.1889 T^{- 0.6034} + 0.9795 \end{matrix}$

表5 不同β 时MTBF区间估计拟合函数 Table 5 Fitting function of MTBF interval estimation with different shape parameter β

由式(7)和表5得到不同形状参数 $\begin{matrix} β \end{matrix}$ 下的MTBF的区间估计变化率函数 $\begin{matrix} Q (T), \end{matrix}$ 如表6和图7所示。

表6 不同β 时MTBF区间估计变化率函数 Table 6 Change rate of MTBF interval estimation with different shape parameter β

形状参数	MTBF区间估计变化率函数
0.5	$\begin{matrix} 3.8210 \times (- 0.8250) T^{(- 0.8250 - 1)} + 0.9259 \times (- 0.1606) T^{(- 0.1606 - 1)} \end{matrix}$
0.8	$\begin{matrix} 2.2980 \times (- 1.3710) T^{(- 1.3710 - 1)} + 0.5181 \times (- 0.3334) T^{(- 0.3334 - 1)} \end{matrix}$
1.0	$\begin{matrix} 1.8220 \times (- 1.8250) T^{(- 1.8250 - 1)} + 0.4496 \times (- 0.3684) T^{(- 0.3684 - 1)} \end{matrix}$
1.2	$\begin{matrix} 1.4390 \times (- 1.9450) T^{(- 1.9450 - 1)} + 0.3696 \times (- 0.4489) T^{(- 0.4489 - 1)} \end{matrix}$
1.5	$\begin{matrix} 1.1200 \times (- 2.4870) T^{(- 2.4870 - 1)} + 0.2855 \times (- 0.6205) T^{(- 0.6205 - 1)} \end{matrix}$
2.0	$\begin{matrix} 0.8590 \times (- 3.002) T^{(- 3.002 - 1)} + 0.2510 \times (- 0.6134) T^{(- 0.6134 - 1)} \end{matrix}$
3.0	$\begin{matrix} 0.4916 \times (- 3.4350) T^{(- 3.4350 - 1)} + 0.1889 \times (- 0.6034) T^{(- 0.6034 - 1)} \end{matrix}$

表6 不同β 时MTBF区间估计变化率函数 Table 6 Change rate of MTBF interval estimation with different shape parameter β

	Figure Option View Download New Window
	图7 不同β 下的MTBF区间估计变化率Fig.7 Change rate of MTBF interval estimation with different shape parameter β

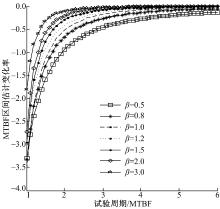
由图7可知, 在满足Q_MTBF=0.2的前提下, 不同 $β$ 时机床的试验周期 $T$ 如表7所示。表7中第三列由第二列乘以 $\begin{matrix} β \end{matrix}$ 所对应的MTBF值得到。

表7 不同β 下的机床试验周期 Table 7 Testing periods with different shape parameter β

由表7和图7可知:随着 $\begin{matrix} β \end{matrix}$ 增加, MTBF区间估计宽度的变化率 $\begin{matrix} Q (T) \end{matrix}$ 改变明显。本例中, 在评估要求Q_MTBF=0.2时, β =1, 即机床进入偶然故障期时, 试验周期 $\begin{matrix} T \end{matrix}$ 约为2.9035倍的MTBF, 即2151.1076 h; 当β < 1, 即机床处于早期故障期时, 试验周期 $\begin{matrix} T 随 β \end{matrix}$ 的减小而延长, 如当β =0.8时, 试验周期约为3.4531倍的MTBF, 即2898.5484 h。而当β =0.5时, 试验周期 $\begin{matrix} T \end{matrix}$ 超过了4.8572倍的MTBF, 即7197.0794 h。当β > 1, 即机床处于损耗期时, 试验周期 $\begin{matrix} T 随 β \end{matrix}$ 值增加而缩短。如, 当β =1.5时, 试验周期为2.2948倍MTBF, 即1534.7950 h。而当β =3时, 试验周期 $\begin{matrix} T \end{matrix}$ 缩短到了1.7207倍的MTBF, 即1138.3792 h。综上, 随着β 的增加, 试验周期 $\begin{matrix} T \end{matrix}$ 缩短。

4 结束语

提出了一种新的数控机床可靠性评估试验的试验周期 $T$ 的设计方法, 解决了试验周期 $T$ 难以确定的问题, 使所设计的试验周期 $T$ 既满足一定的评估精度要求, 又尽可能短。实例分析表明:随着被试机床台数的增加, 试验周期 $T$ 缩短, 本文中, 当多于11台时, 试验周期 $T$ 缩短幅度相对较小。处于不同生命周期阶段, 即 $β$ 值不同时的被试机床的可靠性评估试验的试验周期 $T$ 是不同的, 当 $β$ 增大时, 试验周期 $\begin{matrix} T \end{matrix}$ 缩短。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	杨兆军, 陈传海, 陈菲, 等. 数控机床可靠性技术的研究进展[J]. 机械工程学报, 2013, 49(20): 130-139. Yang Zhao-jun, Chen Chuan-hai, Chen Fei, et al. Progress in the research of reliability technology of machine tools[J]. Journal of Mechanical Engineering, 2013, 49(20): 130-139. [本文引用:1]
[2]	张英芝, 申桂香, 吴甦, 等. 随机截尾数控机床三参数威布尔分布模型[J]. 吉林大学学报: 工学版, 2009, 39(2): 378-381. Zhang Ying-zhi, Shen Gui-xiang, Wu Su, et al. 3-parameter Weibull distribution for rand om truncated NC machine tool fault data[J]. Journal of Jilin University(Engineering and Technology Edition), 2009, 39(2): 378-381. [本文引用:1]
[3]	余闯, 王晓红, 李秋茜. 计数型序贯截尾试验方案的计算与选择[J]. 北京航空航天大学学报, 2014, 40(4): 575-578. Yu Chuang, Wang Xiao-hong, Li Qiu-xi. Calculation and selection of sequentially truncated test scheme[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(4): 575-578. [本文引用:1]
[4]	陈炳锟. 数控机床可靠性试验设计及评估方法研究[D]. 长春: 吉林大学机械科学与工程学院, 2011. Chen Bing-kun. The test design and evaluation method research of reliability project for CNC machine tools[D]. Changchun: College of Mechanical Science and Engineering, Jilin University, 2011. [本文引用:2]
[5]	Mckane S W, Escobar L A, Meeker W Q. Sample size and number of failure requirements for demonstration tests with log-location-scale distributions and failure censoring[J]. Technometrics, 2005, 47(2): 182-190. [本文引用:2]
[6]	何峻, 赵宏钟, 付强. ATR算法识别率的区间估计与样本量分析[J]. 系统工程与电子技术, 2007, 29(7): 1021-1026. He Jun, Zhao Hong-zhong, Fu Qiang. Interval estimation and sample size calculation for ATR algorithm classification accuracy[J]. Systems Engineering and Electronics, 2007, 29(7): 1021-1026. [本文引用:2]
[7]	Guo H R, Pan R. On determining sample size and testing duration of repairable system test[C]∥Proceedings of the 2008 Annual Reliability and Maintainability Symposium. Washington DC, USA: IEEE Computer Society, 2008: 120-125. [本文引用:2]
[8]	杨兆军, 李小兵, 许彬彬. 加工中心时间动态可靠性建模[J]. 机械工程学报, 2012, 48(2): 16-22. Yang Zhao-jun, Li Xiao-bing, Xu Bin-bin, et al. Time dynamic reliability modelling of machining center[J]. Journal of Mechanical Engineering, 2012, 48(2): 16-22. [本文引用:3]
[9]	王智明, 杨建国. 少样本故障数据数控机床的贝叶斯可靠性分析[J]. 中南大学学报: 自然科学版, 2014, 45(12): 4201-4205. Wang Zhi-ming, Yang Jian-guo. Bayesian reliability analysis for numerical control machine tools with small-sized sample failure data[J]. Journal of Central South University(Science and Technology), 2014, 45(12): 4201-4205. [本文引用:3]
[10]	陈传海, 杨兆军, 陈菲, 等. 基于Bootstrap-Bayes的加工中心主轴可靠性建模[J]. 吉林大学学报: 工学版, 2014, 44(1): 95-100. Chen Chuan-hai, Yang Zhao-jun, Chen Fei, et al. Reliability modeling of machining center spindle based on Bootstrap-Bayes[J]. Journal of Jilin University(Engineering and Technology Edition), 2014, 44(1): 95-100. [本文引用:2]
[11]	庞峰. 模拟退火算法的原理及算法在优化问题上的应用[D]. 长春: 吉林大学软件学院, 2006. Pang Feng. The principle of SA algorithm and algorithm's application on optimization problem[D]. Changchun: College of Software, Jilin University, 2006. [本文引用:1]
[12]	Espinheira P L, Ferrari S L P, Cribari-Neto F. Bootstrap prediction intervals in beta regressions[J]. Computational Statistics, 2014, 29(5): 1263-1277. [本文引用:1]
[13]	袁修开, 吕震宙, 岳珠峰. 小样本下分位数函数的Bootstrap置信区间估计[J]. 航空学报, 2012, 33(10): 1842-1849. Yuan Xiu-kai, Lyu Zhen-zhou, Yue Zhu-feng. Bootstrap confidence interval of quantile function estimation for small samples[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(10): 1842-1849. [本文引用:1]

2013

0.0

... 0 引言现场可靠性试验是进行数控机床可靠性评估的基本方法,也是数控机床故障分析和可靠性改进设计的主要数据来源^[1,2] ...

2009

0.0

. 2009, 39(2):378-381

3-parameter Weibull distribution for random truncated NC machine tool fault data

随机截尾数控机床三参数威布尔分布模型

Zhang Ying-zhi , Shen Gui-xiang , Wu Su

张英芝, 申桂香, 吴甦

工程实际中在对数控机床可靠性试验数据进行分析与评估时,多不考虑截尾时间,并多采用二参数威布尔分布,因而数据分析和参数估计中常带来一定误差.针对这一问题,本文提出首先采用故障总时间法进行故障数据预处理,其次假设数据服从二参数威布尔分布并求得相关参数,最后采用改进的插值法来求出位置参数,得出三参数威布尔分布模型.并以6台某系列数控车床1年的28个随机截尾故障数据为例给出具体计算过程,这可以提高数控机床可靠性分析与评价的精确性.

... 0 引言现场可靠性试验是进行数控机床可靠性评估的基本方法,也是数控机床故障分析和可靠性改进设计的主要数据来源^[1,2] ...

2014

0.0

. 2014, 40(4):575-578 DOI:doi:10.13700/j.bh.1001-5965.2013.0295

Calculation and selection of sequentially truncated test scheme

计数型序贯截尾试验方案的计算与选择

Yu Chuang , Wang Xiao-hong , Li Qiu-xi

余闯, 王晓红, 李秋茜

The method for calculating the two types of risk's real value under sequential test scheme was researched, and software for calculating the truncation scheme of test was programed. Then test scheme was analyzed and the relationship between truncated sequential test and fixed number test was studied. Two methods to select the test scheme in the specimen number limited conditions was put forward, the first method is to modest relaxation of risk requirements, and the second is to adjust the test's reception line and reject line which could decrease the maximum required number of trials and keep the two types of risk unchanged. These two methods could determine the testing program flexibly under the specific test requirements, which allow the maximum required number of trials decrease about 30% with the two types of risk or minimum required number of trials increase less than 10%.

研究了计数型序贯试验方案两类风险真实值的计算方法，编程实现了对试验截尾方案的计算.对试验方案进行分析并研究了定数试验与序贯试验的关系，提出了在试件数量受限的情况下确定试验方案的两种方法：适度放宽风险要求，调整接收、拒收线.后者可在保持两类风险不变的情况下降低最大所需试件数.通过这两种方法，能根据具体试验要求灵活地确定试验方案，可使最大所需试件数减少约30%的同时，两类风险或平均所需试件数增大不超过10%.

... 余闯等^[3]和陈炳锟^[4]在综合考虑生产方风险和使用方风险的前提下提出产品交付使用时进行序贯试验的试验件数及试验时间的确定方法 ...

2011

0.0

. 2011, :-

The test design and evaluation method research of reliability project for CNC machine tools

数控机床可靠性试验设计及评估方法研究

Chen Bing-kun

陈炳锟

可靠性试验是获取故障信息、进行可靠性分析、评价、实施可靠性增长等可靠性研究的重要基础,可靠性试验方案合理与否必将影响后续可靠性工作的顺利进行。因此,进行数控机床可靠性试验和评价技术的研究对于快速、准确确定数控机床可靠性薄弱环节、评定其可靠性水平及选择合理措施实施可靠性增长具有重要的理论意义和实际意义。本文在现有可靠性试验研究的基础上,结合数控机床的特点,分别从定时截尾试验、定数截尾试验、序贯试验和基于贝叶斯理论的试验四个方面,并综合考虑生产方风险、使用方风险、鉴别比、MTBF预计值等信息进行可靠性试验方案设计,对于不同试验方案提出相应的数据分析和可靠性评估方法。论文首先针对数控机床服从威布尔分布的特点,将威布尔分布通过参数变换转化为指数分布模式,结合指数分布决策风险方程组,确定数控机床定时截尾试验方案和定数截尾试验并在厂家实施。考虑截尾时间对评估结果的影响,论文采用“故障总时间法”对故障数据进行处理;采用“取中逐步推移检验法”进行异常数据检验;采用“残存比率法”求解经验分布函数;根据故障数据的趋势,建立可靠性模型,根据可靠性模型中的形状参数与定时截尾、定数截尾试验方案设计时选取的形状参数进行对比,验证方案的设计是否合理,进而评价其可靠性水平。其次根据数控机床故障发生个数的概率在威布尔分布下的描述,结合传统序贯试验方案设计方法,确定数控机床的序贯试验方案。由于序贯试验中故障点可能会处于继续试验区而迟迟不能做出判决,通过增加截尾故障数和截尾试验时间的方式,并调整接收线和拒收线以适应决策风险的约束,对数控机床设计出截尾序贯试验方案。由于序贯试验可能出现早早结束试验的情况,会导致故障信息不足而无法准确评估可靠性真值,因此本文基于序贯思想,采用动态截尾试验的方法,对故障数据进行实时的动态采集、动态评估,当可靠性评价指标值的变化处于允许误差的范围内,停止试验。最后,根据数控机床故障率的先验信息,将贝叶斯理论引入到可靠性试验研究中,经贝叶斯的后验风险确定基于贝叶斯理论的定时截尾试验方案。将第2章定时截尾试验中采集到的故障数据应用于贝叶斯试验方案中,由于贝叶斯试验方案的试验时间较短使故障数据呈现小样本类型的特点,采用参数偏差修正方法对该故障数据建立的可靠性模型进行修正和验证,进而评价出可靠性水平。定时或定数截尾试验不仅能做出判决,还能够在试验中得到足够的故障信息,从而可准确评估可靠性指标值。此外,定时截尾试验方案在试验前已确定试验时间及试验台数,便于控制试验的进程,以实现对试验费用和资源的预估;定数截尾试验方案在试验前能确定试验的最大故障数,从而得到足够的故障数据,为故障分析的工作提供基础信息。截尾序贯试验相对于定时和定数截尾试验的平均试验时间短,在只需判决数控机床的可靠性水平是否合格,并不需要评估其指标的情况下,选择截尾序贯试验更为适宜。在厂家急需做出判决,又不愿提高决策风险的情况下,若能够得到准确的故障率先验信息,可采用基于贝叶斯的定时截尾试验方案。

... 余闯等^[3]和陈炳锟^[4]在综合考虑生产方风险和使用方风险的前提下提出产品交付使用时进行序贯试验的试验件数及试验时间的确定方法 ...

... 0]范围内^[4,8,9] ...

2005

0.0

... Mckane等^[5]研究了被试产品服从对数位置-尺度模型时,在不同枢轴量区间估计宽度的要求下确定试验件数和试验时间的试验方案 ...

... 文献[5,6,7]以参数的区间估计的宽度或上、下区间比作为评估要求 ...

2007

0.0

. 2007, 29(7):1021-1026 DOI:doi:10.3321/j.issn:1001-506X.2007.07.001

Interval estimation and sample size calculation for ATR algorithm classification accuracy

ATR算法识别率的区间估计与样本量分析

He Jun , Zhao Hong-zhong , Fu Qiang

何峻, 赵宏钟, 付强

针对雷达ATR性能评估中样本量的特点,从贝叶斯分析角度出发,选取最小长度准则对ATR算法的识别率进行区间估计,主要分析不同估计精度要求下的最小样本量.分析了识别率区间估计的影响因素,分别给出了无先验信息和两类典型有先验信息情况下的识别率区间估计方法和样本量确定准则,得到了识别率估计精度和所需最小样本量的关系.

... 何峻等^[6]以评估参数的区间估计长度最短作为判断依据来确定试验样本量 ...

... 文献[5,6,7]以参数的区间估计的宽度或上、下区间比作为评估要求 ...

2008

0.0

... Guo等^[7]提出以上、下区间估计长度的对数比为评估精度要求来确定可靠性样本试验周期的方法 ...

... 文献[5,6,7]以参数的区间估计的宽度或上、下区间比作为评估要求 ...

2012

0.0

. 2012, 48(2):16-22 DOI:doi:10.3901/JME.2012.02.016

Time dynamic reliability modelling of machining center

加工中心时间动态可靠性建模

Yang Zhao-jun , Li Xiao-bing , Xu Bin-bin

杨兆军, 李小兵, 许彬彬

针对传统加工中心可靠性建模时修复如初的假设与工程实际有一定差异,提出一种加工中心故障发生时间的可靠性建模方法:以经验建模方法为基础,建立待考核加工中心故障发生时间的可靠性函数模型,在不改变故障时序的条件下得到加工中心在考核期内任意时刻的可靠性水平,克服以故障间隔时间的建模方法,仅能描述加工中心某次故障发生后到下次故障发生之前某时刻的可靠性水平变化规律的不足;为分析加工中心各次故障发生时间分布规律,提出加工中心各次故障发生时间的建模方法,并对各次故障发生时间的相关性展开研究。结合被考核加工中心故障发生时间的可靠性函数与各次故障发生时间的可靠性函数,能够完整地描述加工中心可靠性水平随时间动态变化的趋势。以18台加工中心为实例进行分析,建立其故障发生时间与各次故障发生时间的可靠性模型,且通过对实例中加工中心各次故障发生时间的相关性研究表明,加工中心各次故障发生时间之间存在明显的相关关系。

... 对于数控机床,其故障间隔工作时间通常服从威布尔分布^[8,9,10],而上述文献方法均不适用于威布尔分布,不宜直接应用于数控机床的可靠性评估的试验周期的确定 ...

... 1 数控机床可靠性模型许多学者已证明数控机床故障间隔时间服从二参数威布尔分布^[8,9,10],其可靠度函数为: ...

... 0]范围内^[4,8,9] ...

2014

0.0

. 2014, 45(12):4201-4205

Bayesian reliability analysis for numerical control machine tools with small-sized sample failure data

少样本故障数据数控机床的贝叶斯可靠性分析

Wang Zhi-ming , Yang Jian-guo

王智明, 杨建国

应用贝叶斯方法分析少样本故障数据数控机床的可靠性,给出2参数威布尔分布模型参数及数控机床可靠性指标的点估计和区间估计,通过马尔科夫链蒙特卡洛抽样解决了贝叶斯可靠性分析中求解复杂后验积分的难题。结合一具体实例,分析10台加工中心时间截尾的可靠性。计算结果表明:在充分利用先验信息的基础上,贝叶斯方法优于极大似然法和似然比检验法,适合于少样本数据的可靠性分析。

... 1 数控机床可靠性模型许多学者已证明数控机床故障间隔时间服从二参数威布尔分布^[8,9,10],其可靠度函数为: ...

... 0]范围内^[4,8,9] ...

2014

0.0

. 2014, 44(1):95-100 DOI:doi:10.13229/j.cnki.jdxbgxb201401017

Reliability modeling of machining center spindle based on Bootstrap-Bayes

基于Bootstrap-Bayes的加工中心主轴可靠性建模

Chen Chuan-hai , Yang Zhao-jun , Chen Fei

陈传海, 杨兆军, 陈菲

The reliability model established using traditional statistical method for the spindle in machining center with small sample size may be biased in the real case. Therefore, a modified reliability modeling method for small sample size was proposed using Bootstrap-Bayes approach. First, the reliability function of time between failures using empirical modeling method was established. Then the accurate of the parameters prior distribution of Bayes method was provided. This method improves the precision of prior distribution built by traditional empirical method. In order to calculate the posterior distribution of parameters, Monte Carlo simulation was developed. Finally, a real-world example of the spindle of one kind of machining center was presented using the proposed approach to show its potential application. The results show that the proposed method can provide an accurate reliability model for small sample failure data.

针对采用常规Bayes方法对小样本加工中心主轴之类产品进行可靠性建模时与工程实际有较大差异的问题，提出了一种基于Bootstrap-Bayes的小样本可靠性建模方法：为减小先验分布的误差，应用Bootstrap抽样方法对研究对象相同制造环境下同类产品的可靠性模型进行再抽样，从而获得参数的先验分布；在计算后验分布过程中，利用马尔可夫链蒙特卡罗抽样方法，简化了计算，得到了研究对象的可靠性模型。以大样本下经典建模方法所得可靠性模型为基准，与利用Bootstrap-Bayes方法建立的可靠性模型和常规Bayes方法建立的可靠性模型进行比较，结果表明，基于Bootstrap-Bayes的可靠性建模方法所建模型的误差明显小于常规Bayes方法。

... 1 数控机床可靠性模型许多学者已证明数控机床故障间隔时间服从二参数威布尔分布^[8,9,10],其可靠度函数为: ...

2006

0.0

. 2006, :-

The principle of SA algorithm and algorithm's application on optimization problem

模拟退火算法的原理及算法在优化问题上的应用

Pang Feng

庞峰

模拟退火算法是近年来在国内外都比较受关注的算法。它的思想最早在1953年由Metropolis提出，在1983年被Kirkpatrick等人成功引入组合优化领域。由于它具有很强的实用性和极佳的性能表现，迅速引起了很多专家学者的兴趣，不断对其进行研究。本文阐述了模拟退火算法的原理，并从文献角度回顾了近年来较为成功并被广泛采用的对模拟退火算法进行的一些改进，对模拟退火是一种有益的补充。模拟退火算法主要应用在各种优化问题上，函数优化是其中非常重要的一个方面。本文举了两个函数优化的例子，观察应用模拟退火解决这两个问题的表现，并针对实际得到的结果对模拟退火算法的冷却进度表、有限终止性、可行性以及效果和效率进行了进一步的讨论。 NP问题是一个比较麻烦的问题，其解的规模随问题规模的增大而成指数级增长，对于一般的方法而言，当问题规模过大时，就失去了可行性。模拟退火作为一种随机算法，它的特点非常适于求解NP问题，比如著名的旅行商问题(Traveling Salesman Problem)。我们首先介绍了目前比较常用于解决此问题的蚁群算法和分支限界法的原理，然后用模拟退火算法来实现对TSP问题的求解，并将结果与遗传算法的结果进行比较，发现模拟退火算法的表现是令人称道的。由于算法的随机性，最好能结合有记忆的模拟退火算法，让我们得到更好的解。同时，我们还对基于单位风险收益最大化原则的贷款优化组合决策模型进行了讨论，并将改进的模拟退火算法应用于其上。实际的结果表明，模拟退火算法在解决这类问题上有着优异的表现，而且，针对具体的问题，对模拟退火算法进行适当的改进也是完全有必要的。另外，我们还将模拟退火算法应用到一个板式家具下料的工业优化问题上，通过对算法的改进，我们发现算法的表现也值得我们称道。

... 式(5)无解析解,本文采用模拟退火优化算法^[11]求解式(5)中的形状参数 β和尺度参数 η的点估计 ...

2014

0.0

... 该方法通过重抽样来构造Bootstrap样本,常用于计算样本参数的区间估计^[12,13] ...

2012

0.0

. 2012, 33(10):1842-1849

Bootstrap confidence interval of quantile function estimation for small samples

小样本下分位数函数的Bootstrap置信区间估计

Yuan Xiu-kai , Lyu Zhen-zhou , Yue Zhu-feng

袁修开, 吕震宙, 岳珠峰

The tests of aeronautic products are usually small sample cases. In order to analyze the data of small sample tests, a confidence interval estimation method for test population sample quantile function is proposed by combining the maximum entropy method under probability-weighted moment constraints and the Bootstrap method for confidence interval estimation. The maximum entropy method can yield the probability density function under specified moment constraints. When it is subjected to the constraints specified in terms of probability-weighted moment, an unbiased quantile estimate for small samples can be directly obtained. There is no need to integrate form density function to obtain cumulative distribution function which has then to be inverted to obtain the corresponding quantile. The Bootstrap method not only is independent of the distribution of samples in the estimation of the confidence interval but also has wide applications.

航空产品试验一般为小样本试验,为了分析小样本情况下的试验数据,结合以概率加权矩为约束条件的最大熵法和求解置信区间及置信带的Bootstrap方法,提出了一种估计小样本试验件母体分位数函数置信区间的方法。最大熵法在矩约束下能够估计样本的密度函数,而以概率加权矩为约束条件的最大熵法能够针对小样本直接给出分位数的无偏估计,无需由密度函数积分得到累积分布函数,再进行转化得到分位数函数。Bootstrap方法求解置信区间具有不依赖于数据分布的优点,具有广泛的应用范围。

... 该方法通过重抽样来构造Bootstrap样本,常用于计算样本参数的区间估计^[12,13] ...