作者简介:程艳艳(1980-),女,讲师,博士研究生.研究方向:板材成形及数值模拟.E-mail:chengyanyan1980@sina.com
为了提高成形质量,研究了不同单元形式的多点模具柔性拉伸成形。对固定单元和摆头单元多点模具柔性拉伸成形进行了数值模拟,结果表明:摆头单元比固定单元多点模具柔性拉伸成形件表面更光滑,应变分布更均匀,成形精度更高,成形效果更好。对球面件进行了固定单元和摆头单元多点模具柔性拉伸成形试验,验证了其可行性和数值模拟结果的可靠性。
In order to improve the forming quality, the flexible stretch forming processes of multi-point die with different unit forms were studied. The flexible stretch forming processes of multi-point die with fixed unit and with swinging unit were simulated. The numerical results show that the flexible stretch forming part of multi-point die with swinging unit is smoother, the strain distribution is more uniform, the forming accuracy is higher, and forming effect is better than that with fixed unit. Flexible stretch forming experiments of multi-point die with fixed unit and swinging unit were conducted for spherical part. It is proved that flexible stretch forming of multi-point die with swinging unit is feasible and the numerical simulation results are reliable.
为了适应板料产品的复杂化、小批量、生产周期短的特点, 出现了一些新的板料柔性成形技术[1, 2, 3]。多点成形[4, 5]就是一种应用广泛的板料柔性成形技术, 它是将整体模具离散为多个排列规则、高度可调的基本体单元, 通过计算机控制基本体单元高度形成不同的成形曲面[6], 实现成形过程的高效、经济和数字化。多点拉伸成形[7, 8]是以多点成形为基础, 结合传统的整体夹钳进行拉伸成形, 节省了模具设计、制造、调试等时间和费用。多点柔性拉伸成形[9, 10]是在多点拉伸成形的基础上, 利用离散化的思想将整体夹钳离散为多个夹钳, 每个夹钳能够根据模具形状进行自协调运动, 提高拉伸成形质量和材料的利用率。但是在多点柔性拉伸成形过程中, 基本体单元与板料的接触面积小, 在接触点附近板料受到的应力大而且集中, 导致过度的局部变形, 很容易使板料出现压痕、起皱和破裂。摆头单元多点模具柔性拉伸成形技术能够解决这一问题[11, 12], 使离散的模具型面更为连续化, 提高成形质量。
本文利用有限元软件以球面件为研究对象对固定单元和摆头单元多点模具柔性拉伸成形进行数值模拟, 研究了不同单元形式对成形质量的影响, 掌握成形件的应变分布、成形精度等变化规律, 并对模拟结果进行了试验验证。
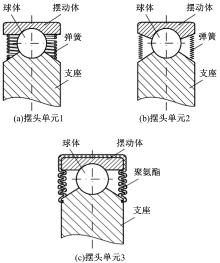
摆头单元多点模具柔性拉伸成形结合了现有多点模具和多夹钳式柔性拉伸成形两种工艺。图1为不同结构的摆头单元, 3种结构中摆头单元都能绕球体在一定范围转动。图1(a)中使用一根弹簧将摆动体和支座柔性联结; 图1(b)中摆动体的形状与图1(a)中不同, 使用对称的4根弹簧将摆动体和支座柔性联结; 图1(c)中使用聚氨酯将摆动体和支座柔性联结来满足板料成形的转动要求。
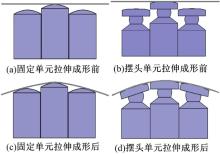
摆头单元多点模具的摆动体可以设置成锥度或者弧度, 本文中采用弧度, 摆头单元如图2所示。图2(a)和图2(c)为固定单元(R=40 mm)多点模具的柔性拉伸成形示意图, 整体模具离散为固定单元, 在拉伸成形前把固定单元调成目标曲面轮廓, 拉伸成形过程中每个单元是固定不动的, 固定单元与板料接触面积较小。图2(b)和图2(d)为摆头单元(R=1000 mm)柔性拉伸成形示意图, 拉伸成形前摆头单元根据目标曲面调整好位置, 摆头单元的摆动体是处于水平状态的。在拉伸成形过程中摆头单元的摆动体受到板料挤压, 在一定范围内逐渐绕球体前后左右转动, 开始时一部分摆头单元发生转动, 然后相邻的摆头单元随之转动。直到摆头单元多点模具型面调整到与目标型面较为吻合, 板料与模具完全贴合, 拉伸成形结束, 所有摆头单元的自适应调形过程停止。摆头单元摆动体包络出目标曲面, 摆头单元与板料之间接触面积较大。由于摆头单元构成的目标曲面基本光顺, 从而板料可以更好地成形。
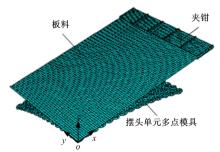
为了更好地分析摆头单元多点模具柔性拉伸成形板料的情况, 利用有限元分析软件ABAQUS/Explicit动态显式算法对摆头单元多点模具柔性拉伸成形的加载过程进行了模拟。模拟材料选用优质碳素结构钢08AL, 密度为7800 kg/m3, 弹性模量为207 GPa, 泊松比为0.30, 屈服强度为270 MPa。模具为R=2000 mm的球面件, 尺寸为1200 mm× 1200 mm。板料尺寸为1600 mm× 1200 mm× 2 mm。数值模拟时, 由于板料是对称形状, 为了节省时间, 建立1/4有限元模型。图3为摆头单元多点模具柔性拉伸成形有限元模型, 由摆头单元多点模具、10个夹钳和板料组成。模具和夹钳在拉伸成形过程中, 几乎不会发生变形, 为了简化模型, 将其设置为刚体单元模型。在数值模拟时, 假定板料为各向同性, 符合Mises屈服准则。模具采用四边形S4R单元和三角形S3单元结合划分网格, 夹钳和板料采用四边形S4R单元划分网格。板料和摆头单元多点模具构成一个接触对, 摩擦因数取0.1, 板料和夹钳构成一个接触对, 摩擦因数取0.5。
图4为不同单元形式的成形件光照效果图, 可以看出固定单元多点模具柔性拉伸成形件表面有明显的压痕和拉形沟缺陷; 摆头单元的成形件表面压痕明显减弱, 拉形沟缺陷明显变浅。摆头单元比固定单元多点模具的柔性拉伸成形件表面更连续, 更加光滑, 显著地提高了成形质量。这是因为摆头单元的半径远大于固定单元, 而且摆头单元的摆动体可以转动到与目标曲面相符的角度, 最终离散的表面与目标曲面较为接近, 板料与模具的接触面更大, 接触更充分。摆头单元多点模具的连续性远高于固定单元, 成形件表面应力集中减小, 使局部变形明显减小且更均匀, 压痕和拉形沟缺陷减小。
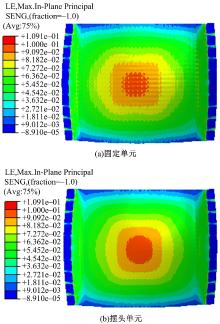
图5为固定单元和摆头单元多点模具柔性拉伸成形件的应变分布。从图中可知, 固定单元和摆头单元成形件在成形区的应变最大值分别为10.01%和9.45%, 应变最小值分别为1.57%和1.25%。摆头单元比固定单元成形件的应变最大值减小5.59%。可以看出, 摆头单元成形件比固定单元成形件的应变分布范围小, 局部起伏也小很多, 分布更加均匀。这是因为在拉伸成形过程中, 摆头单元能够根据目标曲面转动, 改善板料的受力状态, 使应力分布更均匀, 应变也随之分布更均匀。
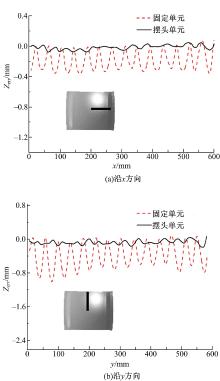
分别提取两种多点模具邻近对称轴的第一行和第一列单元中线对应的成形件应变进行量化分析, 如图6所示。可以看出, 固定单元和摆头单元多点模具柔性拉伸成形件的应变沿
为了进一步对摆头单元多点模具柔性拉伸成形进行研究, 分析其成形误差, 在不使用弹性垫的情况下, 成形件的成形精度可以用
将两种多点模具邻近对称轴的第一行和第一列单元中线对应成形件的成形误差
对摆头单元多点模具柔性拉伸成形进行了试验验证, 试验材料为08AL, 板料尺寸、摆头单元尺寸与数值模拟相同。试验成形件如图8所示, 可以看出, 两种不同单元形式的多点模具柔性拉伸成形件都无拉裂和起皱等缺陷。摆头单元试验成形件的压痕和拉形沟都没有固定单元的明显, 成形表面较为连续光滑, 与数值模拟结果相吻合。验证了摆头单元多点模具柔性拉伸成形的可行性和数值模拟结果的可靠性。
对摆头单元多点模具柔性拉伸成形试验件进行三维光学扫描, 提取了成形件表面的点云数据并与目标球面件进行了比较。成形件的形状误差云图如图9所示, 成形区误差91%分布在-1.13~1.13 mm范围, 误差很小, 成形质量较高, 进一步对数值模拟结果进行了验证。
(1)摆头单元多点模具柔性拉伸成形过程中摆头单元能够绕球体自由转动, 使模具型面更为连续化, 更接近整体模具的成形面。
(2)由数值模拟结果可知, 与固定单元多点模具柔性拉伸成形件相比, 摆头单元拉伸成形件的表面更连续光滑。成形区的应变最大值减小5.59%, 应变分布范围减小2.84%。沿对称轴方向的第一行和第一列压痕最大高度分别减小了76.09%和76.11%, 成形误差明显减小, 成形精度更高。
(3)通过试验对摆头单元多点模具柔性拉伸成形的可行性和数值模拟结果的可靠性进行了验证, 试验结果对实际生产有一定的指导意义。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|