基于延性损伤和剪切损伤的铝合金成形极限预测

引用本文

张学广, 刘纯国, 郑愿, 江仲海, 李湘吉. 基于延性损伤和剪切损伤的铝合金成形极限预测. 2016, 46(5): 1558-1566
ZHANG Xue-guang, LIU Chun-guo, ZHENG Yuan, JIANG Zhong-hai, LI Xiang-ji. Forming limit prediction of aluminum alloy based on ductile damage and shear damage. Journal of Jilin University Engineering and Technology Edition, 2016, 46(5): 1558-1566 复制到剪切板

Permissions

基于延性损伤和剪切损伤的铝合金成形极限预测

张学广, 刘纯国, 郑愿, 江仲海, 李湘吉

吉林大学辊锻工艺研究所,长春 130022

通信作者:刘纯国(1971-),男,教授,博士生导师.研究方向:材料加工工程.E-mail:liucg@jlu.edu.cn

作者简介:张学广(1989-),男,博士研究生.研究方向:材料加工.E-mail:zxg13@mails.jlu.edu.cn

基金:国家自然科学基金项目(51275203).

摘要

针对应用拉伸失稳理论和缺陷理论获取铝合金成形极限图(FLD)的局限性,提出了一种基于延性损伤和剪切损伤的铝合金成形极限的获取方法。通过在损伤过程中引入裂纹状态变量,将FLD的获取转化为计算板材在不同应变路径下断裂时对应的极限主应变。本文以5083-O铝合金为例,设计了简单的缺陷试样加载试验和缺口试样纯剪切试验,利用有限元仿真的方式获取了材料在不同应变率下失效时对应的应力三轴度和剪应力比。通过圆顶冲头涨形的数值模拟,获取了板材在不同应变路径下断裂时对应的冲头行程、极限厚度和断裂成形极限图(FFLD),并与试验结果进行对比。结果表明:数值模拟获取的板材成形极限和试验结果基本吻合。将本文获取的FFLD应用于高速动车组司机室覆盖件的冲压成形效果分析中,预测的成形工件的失效形式和断裂位置与试验结果相吻合。

关键词: 金属材料; 成形极限图; 延性损伤; 剪切损伤; 缺陷预测

中图分类号:TG381 文献标志码:A 文章编号:1671-5497(2016)05-1558-09

Forming limit prediction of aluminum alloy based on ductile damage and shear damage

ZHANG Xue-guang, LIU Chun-guo, ZHENG Yuan, JIANG Zhong-hai, LI Xiang-ji

Roll Forging Research Institute, Jilin University, Changchun 130022, China

Abstract

To overcome the limitation of using tensile instability theory and essential hypothesis to guide the Forming Limit Diagram (FLD) of aluminum alloy, this paper proposes a forming limit prediction method based on ductile damage and shear damage theories. By introducing the macrocrack state variable, the FLD predicting process is transferred to compute the limit principal strain at fracture in various loading paths. The aluminum alloy 5083-O is chosen as the research object. Notched specimen loading test and gapped specimen pure shearing test are done with numerical simulation to obtain the stress triaxiality and shear stress ratio in different strain rates. Dome bulging process is carried out by numerical simulation to obtain the punch strokes, limit thickness and Fracture Forming Limit Diagram (FFLD). Simulation results and experimental results are basically consistent. FFLD is utilized to analyze the stamp forming effects of high-speed train cab covering panel. The predicted defect form and crack location show good agreement with experimental results.

Keyword: metallic material; forming limit diagram; ductile damage; shear damage; forming defect prediction

Show Figures

0 引言

板材成形是金属塑性加工的重要形式, 并广泛应用在汽车、航天等领域。起皱和开裂是板材成形中的主要缺陷, 其中, 开裂严重影响成形件的质量。工业生产中常用成形极限图(FLD)来预测板类件的成形缺陷。获取FLD的理论主要包括拉伸失稳理论(Swift分散性失稳理论^[1]、Hill集中性失稳理论^[2]等)和缺陷理论(Marciniak & Kuczyń ski沟槽假设^[3]、Storen & Rice屈服面尖点假设^[4]等)。拉伸失稳理论多以材料的颈缩作为材料失效的判据, 而对于延伸率较低的铝合金材料, 在断裂前无明显颈缩现象。缺陷理论多假设材料失效是由自身物理性质或屈服模型方面的潜在缺陷导致, 但目前仍缺乏有效的试验证据。因此, 传统的理论在预测铝合金的成形极限方面仍存在不足。20世纪50年代起, 损伤理论开始出现在材料的断裂破坏分析中。损伤理论将材料断裂的过程描述为微孔洞的形核、长大、聚合直至产生宏观裂纹的过程。对于金属材料的损伤, 学者们从微观和宏观两个方面提出了多种不同的损伤准则^{[5, 6, 7, 8, 9]}。其中, 延性损伤准则考虑了塑性变形的加载历程和加载方式对损伤的影响, 因而被广泛应用于材料的破坏分析中。胡莉巾等^[10]将延性损伤准则和有限元模拟相结合, 成功预测了分形旋压过程中裂纹出现的位置。于忠奇等^[11]利用延性损伤准则, 预测了LY12铝合金圆筒件拉深与半球形凸模胀形的成形极限, 并通过试验验证了该准则预测铝合金板材成形极限的准确性。方刚等^[12]利用延性损伤准则, 模拟了冲裁、切削和冷挤压中裂纹起始, 通过模拟结果和试验的对比, 证明了延性损伤准则可以较好地预测金属塑性变形中的宏观断裂。杨玉英等^[13]将延性损伤准则应用到不同材料的盒形件拉深中, 预测了裂纹起始时冲头的临界行程。上述研究多是应用延性损伤准则分析材料在特定加载形式下的破坏。而FLD表征了材料在不同应变路径下的极限变形, 未见有直接将延性损伤准则应用到多种应变路径下材料FLD的获取中的报道。

根据损伤力学的定义, 断裂是变形过程中材料性能逐渐劣化的结果。材料性能劣化的变形过程包含了多种损伤的共同作用, 仅选用延性损伤准则作为材料失效的判据, 难以符合材料在复杂变形条件下的破坏情况。本文以5083-O铝合金板材为研究对象, 提出了一种基于延性损伤和剪切损伤的铝合金板材FLD的获取方法, 将FLD的获取转化为计算板材在不同应变路径下断裂时对应的极限主应变。为了获取材料变形过程中的损伤参数, 本文设计了简单的加载试验来获取材料断裂时的应力三轴度和剪应力比, 综合考虑了加载条件、加载历程和应变率对损伤参数的影响。利用圆顶冲头涨形试验实现了不同加载路径下铝合金板材的破坏。分别利用有限元模拟和试验方式获取了板材断裂时刻的冲头行程、极限厚度和断裂成形极限图(FFLD)。模拟结果和试验结果相吻合。将得到的FFLD应用于高速动车组司机室覆盖件的冲压成形中, 成功预测了成形工件的失效形式和裂纹位置。本文的研究为铝合金板材成形极限获取和成形效果预测提供了依据。

1 裂纹起始判据

1.1 5083-O铝合金

本文研究中, 通过拉伸试验获取5083-O铝合金的材料力学性能参数如下:密度ρ =2.73 g/cm³, 弹性模量E=70.4 GPa, 泊松比ν =0.31, 屈服强度σ ₀=146.7 MPa, 强度系数K=373.7 MPa, 硬化模量n=0.198。

研究表明^[14], 对于5083-O铝合金, 在准静态变形以及应变率小于1000 s^-1的动态变形时, 材料失效前未出现明显的局部颈缩而直接出现宏观裂纹。相比拉伸失稳理论中选择颈缩作为材料失效的判据, 铝合金变形过程中选择断裂作为成形极限的依据更具有实际意义。因此, 使用损伤理论获取铝合金FLD的过程可以转化为计算铝合金在不同变形路径下断裂时对应的极限主应变。

材料破坏的细观力学试验表明, 铝合金材料受载断裂时, 断裂形式有延性断裂, 剪切断裂和混合型断裂。对5083-O铝合金试样的断口分析可知^[15], 在准静态变形条件下, 铝合金的断口由少量带方向性的韧窝和大量的光滑的剪切面组成, 断口较平整光滑, 试样的断裂以剪切断裂为主。随着应变率的提高, 铝合金的断口包含大量的具有方向性的韧窝, 断口形貌比较粗糙, 呈典型的穿晶延性断裂特征。因此, 单独选用延性损伤准则不能准确地描述铝合金在不同加载条件下的断裂行为, 因此, 本文选用延性损伤和剪切损伤相结合的方式来获取铝合金的断裂成形极限。

1.2 裂纹初始条件

材料变形过程中, 当损伤达到一定阈值时, 材料失去承载能力, 损伤单元从材料中去除, 从而形成肉眼可见的宏观裂纹。为了直观地描述变形过程中裂纹的起始情况, 文中设定了裂纹状态变量 $w, w$ 随着变形过程中材料塑性应变的增加而递增。当 $w = 0$ 时, 材料未出现损伤; 当 $0 < w < 1$ 时, 材料为受损状态; 当 $\begin{matrix} w = 1 \end{matrix}$ 时, 材料损伤过程中开始出现宏观裂纹。

延性损伤可以描述为材料变形过程中微孔洞形核、长大和扩展。延性损伤准则考虑了静水压力对材料破坏的影响。假设延性损伤过程中的等效塑性应变 $\begin{matrix} ε^{pl} \end{matrix}$ 是应力三轴度 $\begin{matrix} η \end{matrix}$ 和等效塑性应变率 $\begin{matrix} {\overset{\cdot}{ε}}^{pl} \end{matrix}$ 的函数, 即 $\begin{matrix} ε^{pl} (η, {\overset{\cdot}{ε}}^{pl}), \end{matrix}$ 则延性损伤过程中的裂纹状态变量w_d可以表示为:

$\begin{matrix} w_{d} = \int \frac{d ε^{pl}}{ε_{d}^{pl} (η, {\overset{\cdot}{ε}}^{pl})} (1) \end{matrix}$

式中: $\begin{matrix} η = σ^{H} / σ^{eq}, σ^{H} \end{matrix}$ 为静水压力, $\begin{matrix} σ^{eq} \end{matrix}$ 为Mises等效应力; $\begin{matrix} ε_{d}^{pl} \end{matrix}$ 为延性损伤中断裂时对应的等效塑性应变。

剪切损伤是由材料变形过程中局部剪切带的滑移引起的。剪切损伤考虑了最大切应力对材料破坏的影响。假设剪切损伤过程中的等效塑性应变 $\begin{matrix} ε^{pl} \end{matrix}$ 是剪应力比 $\begin{matrix} θ_{s} \end{matrix}$ 和等效塑性应变率 $\begin{matrix} {\overset{\cdot}{ε}}^{pl} \end{matrix}$ 的函数, 即 $\begin{matrix} ε^{pl} (θ_{s}, {\overset{\cdot}{ε}}^{pl}), \end{matrix}$ 则剪切损伤过程中的裂纹状态变量w_s可以表示为:

$\begin{matrix} w_{s} = \int \frac{d ε^{pl}}{ε_{s}^{pl} (θ_{s}, {\overset{\cdot}{ε}}^{pl})} (2) \end{matrix}$

式中: $\begin{matrix} θ_{s} = \frac{σ^{eq} + k_{s} σ^{H}}{τ_{\max}}; ε_{s}^{pl} \end{matrix}$ 为剪切损伤中断裂时对应的等效塑性应变; $\begin{matrix} τ_{\max} \end{matrix}$ 为最大切应力, 对于铝合金材料, 系数 $\begin{matrix} k_{s} \end{matrix}$ 通常取0.3^[16]。

当裂纹初始是由延性损伤和剪切损伤共同作用时, 裂纹状态变量 $w$ 选择 $w_{d}$ 和 $\begin{matrix} w_{s} \end{matrix}$ 的最大值, 即:

$\begin{matrix} w = \max (w_{d}, w_{s}) (3) \end{matrix}$

2 损伤参数的获取

铝合金的变形行为比较复杂, 获取准确的损伤参数是预测成形极限的关键, 而通过试验获取材料的损伤参数一直是损伤力学研究中的难点。一方面, 试验中为获取损伤参数, 材料损伤必须发生在预定的可直接测量的位置, 避免损伤出现在材料内部等不易测量部位。这往往需要反复进行大量的试验。另一方面, 目前仍缺乏有效的损伤参数的测量工具, 尤其是变形过程中无法实时测试应力等参数。因此, 使用有限元模拟方式进行损伤参数测量^[17]成为获取损伤参数的一种有效手段。

根据1.2节可知, 研究中需要获取的损伤参数为 $\begin{matrix} ε_{d}^{pl} (η, {\overset{\cdot}{ε}}^{pl}) \end{matrix}$ 和 $\begin{matrix} ε_{s}^{pl} (θ_{s}, {\overset{\cdot}{ε}}^{pl}), \end{matrix}$ 即材料在不同应变率下延性损伤失效时的等效塑性应变和应力三轴度, 以及材料在不同应变率下剪切损伤失效时的等效塑性应变和剪应力比。

2.1 缺陷试样加载试验

Bridgman^[18]设计的缺口圆棒拉伸试验是获取断裂应变与应力三轴度之间关系的一种有效方法。然而, Bridgman的方法只适合获取在损伤初始阶段的应力三轴度; 另外, 该方法只考虑了单向拉伸加载条件, 忽略了其他加载形式下断裂应变与应力三轴度的关系。

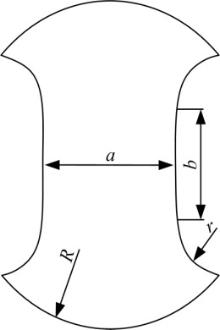
本文设计了缺陷试样加载试验。综合考虑了加载历程和加载路径对三轴度的影响。本文设计的不同加载路径下的二维缺陷试样如图1所示。

	Figure Option View Download New Window
	图1 不同加载路径下的缺陷试样Fig.1 Notched specimens in different loading paths

对于图1中设计的缺陷试样, 加载时断裂肯定发生在预设的缺陷位置(图中圆圈位置)。有限元模拟加载过程中, 选择缺陷处单元应变路径的改变作为试样断裂的标志^[19]。在有限元模拟结果中, 可以直观提取断裂时单元的等效塑性应变。对于断裂时的应力三轴度, 提取缺陷处一系列单元的应力三轴度, 考虑其平均效应。

研究表明^{[20, 21]}, 应力三轴度在材料整个变形过程中是一直变化的, 仅获取断裂时刻的应力三轴度不能反映变形过程中三轴度对材料断裂的影响。因此, 本文考虑了整个变形过程中应力三轴度的累积效应对材料断裂的影响。

基于以上两个方面, 试样断裂时的应力三轴度可以表示为:

$\begin{matrix} η = \frac{\overset{n}{\sum_{i = 1}} \frac{1}{(ε_{d}^{pl})_{i}} \int_{0}^{(} η_{i} d ε^{pl}}{n} (4) \end{matrix}$

式中: $\begin{matrix} n \end{matrix}$ 为缺陷处破坏单元的数目; $\begin{matrix} (ε_{d}^{pl})_{i} \end{matrix}$ 为缺陷处第 $\begin{matrix} i \end{matrix}$ 个单元破坏时对应的等效塑性应变; $\begin{matrix} η_{i} \end{matrix}$ 为缺陷处第 $\begin{matrix} i \end{matrix}$ 个单元损伤过程中的应力三轴度。

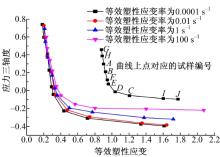
考虑到工业生产中板材通常在中低应变率( $\begin{matrix} {\overset{\cdot}{ε}}^{pl} \end{matrix}$ < 100 s^-1)下成形, 为了研究加载时应变率对断裂应变和三轴度的影响, 模拟中通过改变加载速率实现4种不同等效塑性应变率, 即0.0001、0.01、1、100 s^-1。

获取的不同等效塑性应变率下的等效塑性应变和应力三轴度的关系 $\begin{matrix} ε_{d}^{pl} (η, {\overset{\cdot}{ε}}^{pl}) \end{matrix}$ 如图2所示。可以看出, 在应变路径沿着双向拉伸、单向拉伸、纯剪切、单向压缩、双向压缩的顺序变化中, 试样断裂时刻的等效塑性应变增加, 而应力三轴度降低。在较低等效塑性应变率下( $\begin{matrix} {\overset{\cdot}{ε}}^{pl} \end{matrix}$ < 0.01 s^-1), 曲线对等效塑性应变率的敏感性较低。随着等效塑性应变率的增加, 曲线对等效塑性应变率的敏感性增加, 具体表现为:断裂时对应的等效塑性应变增加, 同时应力三轴度也增加。

	Figure Option View Download New Window
	图2 不同等效塑性应变率下的应力三轴度和等效塑性应变Fig.2 Variation of stress triaxiality with equivalent plastic strain in different equivalent plastic strain rate

2.2 缺口试样纯剪切试验

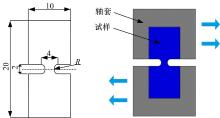
为了获取剪切损伤断裂时等效塑性应变和剪应力比, 本文设计了二维试样的纯剪切试验。设计试样的尺寸和加载方式如图3所示。试样被固定在两轴套之间, 通过轴套的相对运动实现试样的纯剪切断裂。通过改变剪切带的豁口半径, 可实现不同的剪切条件。文中设计15组不同的豁口半径, 分别为1、1.5、2、2.5、3、3.5、4、4.5、5、6、7、8、9、10、20 mm。

	Figure Option View Download New Window
	图3 纯剪切试样的形状和加载方式Fig.3 Geometric shape of the specimen in pure shear

对于图3中设计的豁口试样, 加载时断裂必然发生在试样中部剪切带。有限元模拟加载过程中, 选择轴套上支反力达到最大值作为试样断裂的标志。

与2.1节中相同, 有限元模拟中通过改变加载速率实现4种不同等效塑性应变率, 即0.0001、0.01、1、100 s^-1。本文考虑加载过程的历史效应和平均效应, 获取试样断裂时的剪应力比为:

$\begin{matrix} θ_{s} = \frac{\overset{n}{\sum_{i = 1}} \frac{1}{(ε_{s}^{pl})_{i}} \int_{0}^{(} (θ_{s})_{i} d ε^{pl}}{n} (5) \end{matrix}$

式中: $\begin{matrix} (θ_{s})_{i} \end{matrix}$ 为缺陷处第 $\begin{matrix} i \end{matrix}$ 个单元损伤过程中的剪应力比。

获取的不同等效塑性应变率下的等效塑性应变和剪应力比的关系 $\begin{matrix} ε_{s}^{pl} (θ_{s}, {\overset{\cdot}{ε}}^{pl}) \end{matrix}$ 如图4所示。可以看出, 随着剪切带豁口半径的减小, 试验纯剪切断裂时对应的剪应力比和等效塑性应变同步递增。在较低等效塑性应变率下( $\begin{matrix} {\overset{\cdot}{ε}}^{pl} \end{matrix}$ < 0.01 s^-1), 曲线对等效塑性应变率的敏感性较低。随着等效塑性应变率的增加, 曲线对等效塑性应变率的敏感性增加, 具体表现为:断裂时对应的等效塑性应变增加。

	Figure Option View Download New Window
	图4 不同等效塑性应变率下的剪应力比和等效塑性应变Fig.4 Variation of shear stress ratio with equivalent plastic strain in different equivalent plastic strain rate

3 成形极限的获取

圆顶冲头涨形试验是获取板料成形极限的一种简单有效的方法。试验中, 试样悬空放置在模具和压边圈之间, 通过圆顶冲头涨形直至破裂, 该过程中摩擦对板材破裂的影响较小。通过改变试样有效成形区域的面积, 可以实现不同加载路径下的破坏。

本文设计的试样形状和尺寸见图5和表1。

	Figure Option View Download New Window
	图5 试样的形状Fig.5 Geometric shape of the specimen

表1 试样的尺寸 Table 1 Geometric dimensions of specimens

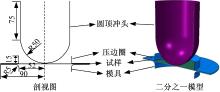
本文选用有限元软件Abaqus/Explicit对圆顶冲头的涨形过程进行模拟, 其有限元模型如图6所示, 其主要组成包括圆顶冲头、压边圈、试样和模具。试样的厚度为1 mm。模拟中忽略冲头、模具和压边圈的变形, 将其简化为刚体壳结构。模拟中选用压边力为15 t, 并在模具上设置虚拟拉延筋以提升进料阻力。试样和压边圈以及模具之间的摩擦因数设置为0.2; 考虑到试样和冲头之间的接触条件为油润滑, 二者之间的摩擦因数设置为0.05。冲头的加载速率为1 mm/s。模拟中采用了有效的单元删除技术, 当变形过程中单元的裂纹状态变量达到1时, 失效单元就会从试样中删除, 形成可见的宏观裂纹。

	Figure Option View Download New Window
	图6 圆顶冲头涨形的有限元模型Fig.6 FE model of dome bulging process

9组不同试样裂纹初始位置和对应的裂纹状态变量如图7所示。可以看出, 在单向拉伸条件下, 涨形时裂纹出现在试样有效成形区域的两侧; 在平面应变条件下, 裂纹逐渐向中心移动; 在双向拉伸条件下, 裂纹出现在试样有效成形区域的中心位置。

	Figure Option View Download New Window
	图7 试样的裂纹初始位置Fig.7 Crack initiation of specimen

4 结果分析

为了验证数值模拟中基于延性损伤和剪切损伤获取的铝合金的成形极限, 本文利用EC1200数控涨形机进行了试验验证。涨形过程中, 冲头和试样之间使用润滑油改善二者之间的摩擦, 当试样表面出现宏观裂纹时, 试验终止。

4.1 冲头行程

冲头行程反映了试样在特定加载路径下的极限变形。试验中, 利用数控涨形机记录裂纹初始时冲头的极限行程, 并与模拟结果进行对比, 如图8所示。

	Figure Option View Download New Window
	图8 冲头行程对比Fig.8 Comparison of punch stroke

从图8可以看出, 模拟结果中, 变形路径从单向拉伸到平面应变的变化过程中, 冲头行程递减; 从平面应变到双向拉伸的变化过程中, 冲头行程递增。试验结果中, 单向拉伸条件下对应的冲头行程最大, 平面应变条件下对应的冲头行程最小。试验结果和模拟结果的最大误差为1.1 mm, 说明模拟结果和试验结果相吻合。

4.2 极限厚度

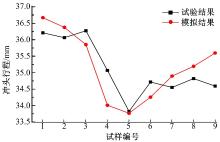
极限厚度表征了板材在裂纹初始时的最大减薄量, 并可以作为极限应变的参照。试验中, 利用超声波测厚仪获取试样裂纹附近的平均极限厚度; 模拟结果中, 选择裂纹临近的5个单元提取极限厚度并计算其平均值。模拟结果和试验结果中极限厚度的对比如图9所示。

	Figure Option View Download New Window
	图9 极限厚度对比Fig.9 Comparison of limit thickness

从图9可以看出, 模拟结果和试验结果表现出相同的趋势, 在平面应变情况下, 裂纹初始时对应的极限减薄量最小, 试样的极限厚度最大; 在双向拉伸情况下, 裂纹初始时对应的极限减薄量最大, 试样的极限厚度最小。对于单个试样, 图9中极限厚度和图8中的冲头行程呈相反的趋势, 裂纹初始时对应的冲头行程越大, 减薄量也越大, 试样的极限厚度也越小。由于数值模拟中理想的材料参数和良好的摩擦条件, 在单向拉伸和双向拉伸条件下, 裂纹初始时对应的冲头行程更大, 相应的极限厚度也越小。试验结果和模拟结果的最大误差为0.08 mm, 说明模拟结果和试验结果相吻合。

4.3 成形极限图

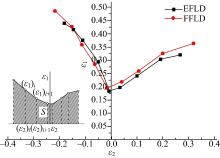
试验前在试样上印制网状分布的圆点, 对涨形后的试样采用GOM光学应变测量仪测量裂纹附近的第一主应变 $\begin{matrix} ε_{1} \end{matrix}$ 和第二主应变 $\begin{matrix} ε_{2}, \end{matrix}$ 并以此绘制板材的试验成形极限图(EFLD); 对于模拟结果, 提取裂纹附近5个单元的 $\begin{matrix} ε_{1} \end{matrix}$ 和 $\begin{matrix} ε_{2} \end{matrix}$ 并计算平均值, 以此绘制板材的断裂成形极限图(FFLD)。成形极限图的对比如图10所示。

	Figure Option View Download New Window
	图10 FLD对比Fig.10 Comparison of FLD

从图10可以看出, 由于数值模拟中理想的材料参数和良好的摩擦条件, FFLD曲线的跨度大于EFLD的跨度; FFLD曲线的最低点(平面应变点)也高于EFLD曲线的最低点。FFLD和EFLD在左侧单向拉伸区域重合度较高, 在右侧双向拉伸区域, FFLD高于EFLD。可以认为模拟中获取的板材成形极限高于试验中获取的板材成形极限。

FLD曲线是由9组试样断裂时对应的极限应变点构成的, 为了评估EFLD与FFLD之间的误差, 本文分别考虑了FLD中极限应变点的个体偏差和群体偏差。

个体偏差是指两组FLD中对应的单个极限应变点之间的位置偏差。极限应变点的个体偏差可以由对应极限应变点之间的位置差方和 $\begin{matrix} d \end{matrix}$ 表示:

$\begin{matrix} d = \overset{9}{\sum_{i = 1}} {[(ε_{f 1})_{i} - (ε_{e 1})_{i}]^{2} + [(ε_{f 2})_{i} - (ε_{e 2})_{i}]^{2}} (6) \end{matrix}$

式中: $\begin{matrix} i \end{matrix}$ 为极限应变点编号; $\begin{matrix} (ε_{f 1})_{i} \end{matrix}$ 和 $\begin{matrix} (ε_{f 2})_{i} \end{matrix}$ 分别为FFLD中第 $\begin{matrix} i \end{matrix}$ 个极限应变点的第一主应变和第二主应变; $\begin{matrix} (ε_{e 1})_{i} \end{matrix}$ 和 $\begin{matrix} (ε_{e 2})_{i} \end{matrix}$ 分别为EFLD中第 $\begin{matrix} i \end{matrix}$ 个极限应变点的第一主应变和第二主应变。两组FLD极限应变点之间的个体偏差为0.0103。

群体偏差是指两组FLD中所有极限应变点之间的分布偏差。工程应用中, FLD曲线以下的部分为安全成形区域, 其面积受所有极限应变点分布和位置的直接影响。本文选用FLD曲线在 $\begin{matrix} ε_{2} \end{matrix}$ 轴上的投影面积 $\begin{matrix} s \end{matrix}$ 来衡量极限应变点的群体偏差。由于FLD曲线在 $\begin{matrix} ε_{2} \end{matrix}$ 轴上的投影可以分解为一系列由相邻极限应变点构成的梯形区域, 因此 $\begin{matrix} s \end{matrix}$ 可以表述为:

$\begin{matrix} s = \overset{8}{\sum_{i = 1}} {\frac{1}{2} [(ε_{1})_{i + 1} + (ε_{1})_{i}] [(ε_{2})_{i + 1} - (ε_{2})_{i}]} (7) \end{matrix}$

式中: $\begin{matrix} (ε_{1})_{i} \end{matrix}$ 和 $\begin{matrix} (ε_{2})_{i} \end{matrix}$ 分别为第 $\begin{matrix} i \end{matrix}$ 个极限应变点的第一主应变和第二主应变。

对于EFLD, s_e为0.131; 对于FFLD, s_f为0.168。两组FLD极限应变点之间的群体偏差为0.037。

FFLD与EFLD中极限应变点个体误差小于0.015, 群体误差小于0.04, 表明FFLD和EFLD相吻合。

5 试验验证

为了验证基于损伤理论和有限元模拟方式获取的FFLD在工业生产中的实际应用效果, 本文以高速动车组司机室曲面覆盖件的冲压成形为例, 应用FFLD分析板材的冲压成形效果。板材为5083-O铝合金, 厚度为1 mm。曲面覆盖件的目标形状如图11所示, 目标形状包含半径为12 mm的棱线, 在实际冲压成形中, 棱线位置易发生断裂。

	Figure Option View Download New Window
	图11 工件的目标形状Fig.11 Geometric shape of the covering panel

本文利用Abaqus/Explicit软件对曲面覆盖件的冲压过程进行模拟。模拟中, 覆盖件采用对压方式成形, 压边力设置为80 t, 模具和板材之间的摩擦因数设置为0.05, 单个冲压成形周期为10 s。

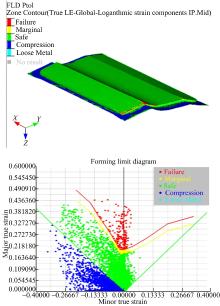
将成形后的工件导入后处理软件Hyperview中, 利用上文获取的FFLD分析其成形效果, 如图12所示。在Hyperview中, 根据成形后板材的主应力在FFLD中的分布将成形后的工件分为4个区域, FFLD曲线以上的部分为开裂区(图中为红色); FFLD曲线下移10%作为临界线, 临界线和FFLD曲线之间的部分为开裂趋势区(图中为黄色); 临界线和双侧45° 线之间的部分为安全成形区(图中为绿色); 双侧45° 线以下的部分为受压区(图中为蓝色)。

	Figure Option View Download New Window
	图12 工件成形效果预测Fig.12 Prediction on the forming effect

工件成形效果预测和主应力分布如图12所示。可以看出, 成形后工件曲面大部分位于安全成形区域, 工件外围固定位置为受压状态。一条棱线部位发生开裂, 另一条棱线边缘部位有开裂趋势。

实际生产中采用800 t油压机进行工件冲压成形。压边力为80 t, 模具和板材之间采用油润滑, 试验过程和试验结果如图13所示。成形后工件一侧棱线部位发生开裂, 与预测结果相吻合。

	Figure Option View Download New Window
	图13 冲压成形过程以及成形件Fig.13 Stamp forming process and formed workpiece

6 结论

(1)相比于颈缩, 5083-O铝合金变形过程中选用断裂作为材料失效的判据更为合理。

(2)本文利用延性损伤和剪切损伤理论指导铝合金成形极限的获取, 定义了损伤过程中的裂纹初始变量。利用数值模拟的方式获取了材料损伤参数, 综合考虑了加载历程和加载路径对损伤参数的影响。

(3)分别利用数值模拟和试验的方式进行了圆顶冲头涨形试验。获取了裂纹初始时的冲头行程、极限厚度和成形极限图。对比表明, 模拟结果和试验结果相吻合。证明利用损伤理论和有限元模拟的方式可快速、准确预测铝合金板料的成形极限。

(4)将本文获取的断裂成形极限图应用于高速动车组司机室曲面覆盖件的冲压成形中, 成功预测了工件的失效形式和裂纹位置。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Swift H W. Plastic instability under plane stress[J]. Journal of the Mechanics and Physics of Solids, 1952, 1(1): 1-18. [本文引用:1]
[2]	Hill R. On discontinuous plastic states with special reference to localized necking in thin sheets[J]. Journal of the Mechanics and Physics of Solids, 1952, 1(1): 19-30. [本文引用:1]
[3]	Marciniak Z, Kuczyński K. Limit strains in the processes of stretch-forming sheet metal[J]. International Journal of Mechanical Sciences, 1967, 9(9): 609-620. [本文引用:1]
[4]	Storen S, Rice J R. Localized necking in thin sheets[J]. Journal of the Mechanics and Physics of Solids, 1975, 23(6): 421-431. [本文引用:1]
[5]	McClintock F A. A criterion for ductile fracture by the growth of holes[J]. Journal of Applied Mechanics, 1968, 35(2): 363-371. [本文引用:1]
[6]	姜薇, 李亚智, 束一秀, 等. 基于微孔贯通细观损伤模型的金属韧性断裂分析[J]. 工程力学, 2014, 31(10): 27-32. Jiang Wei, Li Ya-zhi, Shu Yi-xiu, et al. Investigation of metallic ductile fracture by void-based meso-damage model[J]. Engineering Mechanics, 2014, 31(10): 27-32. [本文引用:1]
[7]	张多新, 屈文俊, 王清云, 等. 准脆性材料的弹塑性各向异性损伤耦合本构模型研究[J]. 固体力学学报, 2012, 33(2): 199-208. Zhang Duo-xin, Qu Wen-jun, Wang Qing-yun, et al. Research on the coupled anisotropic damage and plasticity constitutive model for quasi-brittle materials[J]. Acta Mechanica Solida Sinica, 2012, 33(2): 199-208. [本文引用:1]
[8]	Rice J R, Tracey D M. On the ductile enlargement of voids in triaxial stress fields[J]. Journal of the Mechanics and Physics of Solids, 1969, 17(3): 201-217. [本文引用:1]
[9]	庄蔚敏, 曹德闯, 叶辉. 基于连续介质损伤力学预测7075铝合金热冲压成形极限图[J]. 吉林大学学报: 工学版, 2014, 44(2): 409-414. Zhuang Wei-min, Cao De-chuang, Ye Hui. Prediction of FLD for AA7075 under hot stamping based on continuum damage mechanics[J]. Journal of Jilin University(Engineering and Technology Edition), 2014, 44(2): 409-414. [本文引用:1]
[10]	胡莉巾, 詹梅, 黄亮, 等. 采用韧性断裂准则预测分形旋压径向开裂[J]. 塑性工程学报, 2009, 16(3): 69-73. Hu Li-jin, Zhan Mei, Huang Liang, et al. Prediction of radial crack of the workpiece during the splitting spinning based on ductile fracture criteria[J]. Journal of Plasticity Engineering, 2009, 16(3): 69-73. [本文引用:1]
[11]	于忠奇, 杨玉英, 王永志, 等. 基于韧性断裂准则的铝合金板材成形极限预测[J]. 中国有色金属学报, 2003, 13(5): 1223-1226. Yu Zhong-qi, Yang Yu-ying, Wang Yong-zhi, et al. Forming limit prediction of aluminimu alloy sheet based on ductile failure[J]. The Chinese Journal of Nonferrous Metals, 2003, 13(5): 1223-1226. [本文引用:1]
[12]	方刚, 雷丽萍, 曾攀. 金属塑性成形过程延性断裂的准则及其数值模拟[J]. 机械工程学报, 2002, 38(增刊1): 21-25. Fang Gang, Lei Li-ping, Zeng Pan. Prediction and numerical simulation on the ductile damage in metal ductile forming process[J]. Chinese Journal of Mechanical Engineering, 2002, 38(Sup. 1): 21-25. [本文引用:1]
[13]	杨玉英, 于忠奇, 王永志, 等. 应用韧性断裂准则预测盒形件拉深成形极限[J]. 哈尔滨工业大学学报, 2004, 36(11): 1507-1510. Yang Yu-ying, Yu Zhong-qi, Wang Yong-zhi, et al. The application of a ductile fracture criterion to the predicton of the forming limit in quadrate-cup deep drawing[J]. Journal of Harbin Institute of Technology, 2004, 36(11): 1507-1510. [本文引用:1]
[14]	刘守法, 蔡云, 吴松林. 5083铝合金低温超塑变形机理[J]. 兵器材料科学与工程, 2014, 37(4): 33-35. Liu Shou-fa, Cai Yun, Wu Song-lin. Superplastic deformation mechanism of 5083 aluminum alloy at low temperature[J]. Ordnance Material Science and Engineering, 2014, 37(4): 33-35. [本文引用:1]
[15]	Topping T D, Hu T, Manigand an K, et al. Quasi-static deformation and final fracture behaviour of aluminium alloy 5083: influence of cryomilling[J]. Philosophical Magazine, 2013, 93(8): 899-921. [本文引用:1]
[16]	Hooputra H, Gese H, Dell H, et al. A comprehensive failure model for crashworthiness simulation of aluminium extrusions[J]. International Journal of Crashworthiness, 2004, 9(5): 449-463. [本文引用:1]
[17]	李国弘, 闫家益, 李荣, 等. LY12BCZYU铝合金韧性渐进损伤模型参数反演[J]. 兵器材料科学与工程, 2014, 37(2): 101-105. Li Guo-hong, Yan Jia-yi, Li Rong, et al. Parameter inversion for ductile progressive damage model of LY12BCZYU[J]. Ordnance Material Science and Engineering, 2014, 37(2): 101-105. [本文引用:1]
[18]	Bridgman P W. Studies in large plastic flow and fracture with special emphasis on the effects of hydrostatic pressure[D]. New York: Harvard University, 1952. [本文引用:1]
[19]	徐岩, 王辉, 王娟, 等. 板料拉伸失稳时的应变路径分析[J]. 南京航空航天大学学报, 2012, 44(2): 246-250. Xu Yan, Wang Hui, Wang Juan, et al. Investigation on local necking of sheet metal forming based on strain-path analysis[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2012, 44(2): 246-250. [本文引用:1]
[20]	Bao Y B, Wierzbicki T. A comparative study on various ductile crack formation criteria[J]. Journal of Engineering Materials and Technology -Transactions of the ASME, 2004, 126(3): 314-324. [本文引用:1]
[21]	Bao Y B, Wierzbicki T. On fracture locus in the equivalent strain and stress triaxiality space[J]. International Journal of Mechanical Sciences, 2004, 46(1): 81-98. [本文引用:1]

1952

0.0

... 获取FLD的理论主要包括拉伸失稳理论(Swift分散性失稳理论^[1]、Hill集中性失稳理论^[2]等)和缺陷理论(Marciniak #cod#x00026 ...

1952

0.0

... 获取FLD的理论主要包括拉伸失稳理论(Swift分散性失稳理论^[1]、Hill集中性失稳理论^[2]等)和缺陷理论(Marciniak #cod#x00026 ...

1967

0.0

... ski沟槽假设^[3]、Storen #cod#x00026 ...

1975

0.0

... Rice屈服面尖点假设^[4]等) ...

1968

0.0

... 对于金属材料的损伤,学者们从微观和宏观两个方面提出了多种不同的损伤准则^[5,6,7,8,9] ...

2014

0.0

. 2014, 31(10):27-32 DOI:doi:10.6052/j.issn.1000-4750.2013.04.0351

Investigation of metallic ductile fracture by void-based meso-damage model

基于微孔贯通细观损伤模型的金属韧性断裂分析

Jiang Wei , Li Ya-zhi , Shu Yi-xiu

姜薇, 李亚智, 束一秀

韧性材料断裂过程通常可看作是材料内部微孔洞的形核、扩展及相互贯通的积累。经典的GursonTvergaard(GT)模型能够很好地模拟具有变形均匀、各向同性的孔洞的萌生及扩展过程;但无法模拟由孔洞贯通而引起的局部变形过程,因此需要对其修正,引入相应的孔洞贯通准则。该文采用两种贯通准则对经典GT模型进行修正,即Thomason的塑性极限载荷准则和临界等效塑性应变准则。借助用户自定义程序UMAT将采用这两种贯通准则修正的GT本构关系嵌入至商用有限元软件ABAQUS中,从而可通过对金属材料应力状态和断裂机理的分析控制孔洞的贯通。以一组含有不同缺口根半径的圆棒拉伸试验件为例,分析了该类金属构件自孔洞萌生至最终断裂的整个损伤演化过程,并与试验数据进行了对比,验证了该模型的有效性。该文还讨论了金属断裂过程中应力三轴度对微裂纹萌生与扩展的影响。

... 对于金属材料的损伤,学者们从微观和宏观两个方面提出了多种不同的损伤准则^[5,6,7,8,9] ...

2012

0.0

. 2012, 33(2):199-208 DOI:doi:10.3969/j.issn.0254-7805.2012.02.010

Research on the coupled anisotropic damage and plasticity constitutive model for quasi-brittle materials

准脆性材料的弹塑性各向异性损伤耦合本构模型研究

Zhang Duo-xin , Qu Wen-jun , Wang Qing-yun

张多新, 屈文俊, 王清云

针对准脆性材料的非线性特征,在热动力学框架内,建立了准脆性材料的弹塑性与各向异性损伤耦合的本构关系.对准脆性材料的变形机理和损伤诱发的各向异性进行了诠释,并给出了损伤构形和有效构形中各物理量之间的关系.在有效应力空间内,建立了塑性屈服准则、拉压不同的塑性随动强化法则和各向同性强化法则.在损伤构形中,采用应变能释放率,建立了拉压损伤准则、拉压不同的损伤随动强化法则和各向同性强化法则.基于塑性屈服准则和损伤准则,构建了塑性势泛函和损伤势泛函,并由正交性法则,给出了塑性和损伤强化效应内变量的演化规律,同时,联立塑性屈服面和损伤加载面,给出了塑性流动和损伤演化内变量的演化法则.将损伤力学和塑性力学结合起来,建立了应变驱动的应力-应变增量本构关系,给出了本构数值积分的要点.以单轴加载-卸载往复试验识别和校准了材料常数,并对简单试验进行了预测,结果表明,所建本构模型对准脆件材料的非线性材料性能有良好的预测能力.

... 对于金属材料的损伤,学者们从微观和宏观两个方面提出了多种不同的损伤准则^[5,6,7,8,9] ...

1969

0.0

... 对于金属材料的损伤,学者们从微观和宏观两个方面提出了多种不同的损伤准则^[5,6,7,8,9] ...

2014

0.0

. 2014, 44(2):409-414 DOI:doi:10.13229/j.cnki.jdxbgxb201402021

Prediction of FLD for AA7075 under hot stamping based on continuum damage mechanics

基于连续介质损伤力学预测7075铝合金热冲压成形极限图

Zhuang Wei-min , Cao De-chuang , Ye Hui

庄蔚敏, 曹德闯, 叶辉

In view of the limitation of the Forming Limit Diagram (FLD), which is used to evaluate the formability of AA7075 under hot stamping conditions, the continuum damage mechanics was introduced into the prediction of the FLD. A set of uniaxial damage constitutive equations was presented and the material constants were optimized. Based on the analysis of the features of Forming Limit Curves (FLCs) for AA7075 at different temperatures, a plane-stress damage equation was proposed to take account of the damage of material at different stress-strain state. Then the FLCs were predicted on the condition of four sets of temperatures and three sets of strain rates. The results indicate that the stress-strain curves of the numerical analysis of uniaxial damage constitutive equation and the experimental curves are basically consistent. Using the plane-stress unified viscoplastic damage constitutive equations can predict the FLD at different temperature and strain rate in the hot stamping process and provide the failure criteria.

针对应用试验方法获得的7075-T6铝合金板材热冲压成形极限图（FLD）的局限性，开展了基于连续介质损伤力学预测7075铝合金热成形FLD的方法研究。提出应用一组单轴黏塑性损伤本构方程并优化材料常数，建立了平面应力损伤本构方程，通过分析7075铝合金在不同温度时成形极限曲线（FLC）的特点，得出不同应力状态对损伤的影响，预测7075-T6铝合金板材在四组温度和三组应变率下的FLC。研究结果表明，基于单轴损伤本构方程进行数值分析得到的应力-应变曲线与试验曲线基本吻合。应用平面应力黏塑性损伤本构方程能够预测铝合金板材热冲压过程中不同温度和应变率的FLD，为铝合金板材热冲压过程提供失效判断依据。

... 对于金属材料的损伤,学者们从微观和宏观两个方面提出了多种不同的损伤准则^[5,6,7,8,9] ...

2009

0.0

. 2009, 16(3):69-73 DOI:doi:10.3969/j.issn.1007-2012.2009.03.014

Prediction of radial crack of the workpiece during the splitting spinning based on ductile fracture criteria

采用韧性断裂准则预测分形旋压径向开裂

Hu Li-jin , Zhan Mei , Huang Liang

胡莉巾, 詹梅, 黄亮

径向开裂是分形旋压过程中工件的主要破坏形式,严重制约着该类零件旋压成形极限的提高.由于分形旋压成形过程本身的复杂性,使得预测其径向开裂缺陷,并确定该类工件的成形极限成为难点.基于商用有限元软件ABAQUS/Explicit提供的VUMAT二次开发平台,将Cockcroft-Latham和Lemaitre韧性断裂准则嵌入到有限元数值模拟中,建立了预测分形旋压径向开裂的有限元模型.结果表明,该模型较之Cockcroft-Latham准则、Lemaitre 准则,能够更准确地预测分形旋压工件损伤值的分布及其开始出现的位置和时刻.

... 胡莉巾等^[10]将延性损伤准则和有限元模拟相结合,成功预测了分形旋压过程中裂纹出现的位置 ...

2003

0.0

. 2003, 13(5):1223-1226 DOI:doi:10.3321/j.issn:1004-0609.2003.05.034

Forming limit prediction of aluminimu alloy sheet based on ductile failure

基于韧性断裂准则的铝合金板材成形极限预测

Yu Zhong-qi , Yang Yu-ying , Wang Yong-zhi

于忠奇, 杨玉英, 王永志

为了准确地预测铝合金板材成形极限, 将韧性断裂准则引入到数值模拟中. 在数值模拟获得的应力应变值基础上, 采用简单拉伸试验和数值模拟相结合的方法确定了韧性断裂准则中的材料常数, 并应用该韧性断裂准则预测了铝合金LY12(M)的圆筒件拉深和半球形凸模胀形的成形极限. 预测结果与实验值吻合较好, 该韧性断裂准则能够预测铝合金板材成形极限.

... 于忠奇等^[11]利用延性损伤准则,预测了LY12铝合金圆筒件拉深与半球形凸模胀形的成形极限,并通过试验验证了该准则预测铝合金板材成形极限的准确性 ...

2002

0.0

. 2002, 38(增刊1):21-25 DOI:doi:10.3321/j.issn:0577-6686.2002.z1.005

Prediction and numerical simulation on the ductile damage in metal ductile forming process

金属塑性成形过程延性断裂的准则及其数值模拟

Fang Gang , Lei Li-ping , Zeng Pan

方刚, 雷丽萍, 曾攀

介绍了一些对金属延性断裂进行判断的准则,包括基于试验的经验性准则以及连续损伤力学方法建立的准则.在金属塑性成形的大变形有限元分析过程中,将会对断裂裂纹的生成及扩展进行模拟,介绍使用单元删除、单元分裂以及单元分离技术来处理出现裂纹后的工件网格,就齿圈压板精密冲裁、切削加工中切屑成形以及冷挤压等复杂工艺过程的断裂现象进行了模拟研究.

... 方刚等^[12]利用延性损伤准则,模拟了冲裁、切削和冷挤压中裂纹起始,通过模拟结果和试验的对比,证明了延性损伤准则可以较好地预测金属塑性变形中的宏观断裂 ...

2004

0.0

. 2004, 36(11):1507-1510 DOI:doi:10.3321/j.issn:0367-6234.2004.11.023

The application of a ductile fracture criterion to the predicton of the forming limit in quadrate-cup deep drawing

应用韧性断裂准则预测盒形件拉深成形极限

Yang Yu-ying , Yu Zhong-qi , Wang Yong-zhi

杨玉英, 于忠奇, 王永志

目前已提出的韧性断裂准则预测板料成形极限,只在简单轴对称件中得到应用.利用作者提出的韧性断裂准则预测了铝合金板LF21,LY21(M)和钢板st17非轴对称的方盒件拉深成形极限,并与成形极限图的预测结果和实验结果进行比较.结果表明,这种方法较好地预测了盒形件拉深成形极限,为预测非轴对称件成形的断裂发生提供了一种有效的方法,也为预测复杂形状零件成形极限奠定了基础.

... 杨玉英等^[13]将延性损伤准则应用到不同材料的盒形件拉深中,预测了裂纹起始时冲头的临界行程 ...

2014

0.0

. 2014, 37(4):33-35

Superplastic deformation mechanism of 5083 aluminum alloy at low temperature

5083铝合金低温超塑变形机理

Liu Shou-fa , Cai Yun , Wu Song-lin

刘守法, 蔡云, 吴松林

采用温轧及退火的组合工艺对5083铝合金进行加工,在250℃下以1×10-3s-1初始应变速率对试样进行拉伸试验,并利用塑性异向性值R对试样拉伸过程中的颈缩现象进行分析,对拉伸过程中试样最大局部真应变处的TEM图像和电子衍射花样进行观察。结果表明:最大局部真应变值为1.31处的R值趋近于0.8,预测其颈缩不会恶化而得到不错的伸长率;随着拉伸的进行,晶粒尺寸增大而晶粒间的位错密度却减小,晶粒也从拉伸前的[110]及[112]织构组织转换成较散乱分布的晶粒取向。

... 研究表明^[14],对于5083-O铝合金,在准静态变形以及应变率小于1000 s^-1的动态变形时,材料失效前未出现明显的局部颈缩而直接出现宏观裂纹 ...

2013

0.0

... 对5083-O铝合金试样的断口分析可知^[15],在准静态变形条件下,铝合金的断口由少量带方向性的韧窝和大量的光滑的剪切面组成,断口较平整光滑,试样的断裂以剪切断裂为主 ...

2004

0.0

... 3^[16] ...

2014

0.0

. 2014, 37(2):101-105

Parameter inversion for ductile progressive damage model of LY12BCZYU

LY12BCZYU铝合金韧性渐进损伤模型参数反演

Li Guo-hong , Yan Jia-yi , Li Rong

李国弘, 闫家益, 李荣

为准确仿真LY12BCZYU铝合金连接件的动态韧性失效过程,将延性失效模型和剪切失效模型联用来预测损伤起始和演化,分析损伤参数影响结构响应的规律,并根据试验结果对损伤参数进行反演推定。得到LY12BCZYU延性损伤模型和剪切损伤模型的损伤起始参数和失效塑性位移,计算结果与试验结果符合较好。

... 因此,使用有限元模拟方式进行损伤参数测量^[17]成为获取损伤参数的一种有效手段 ...

1952

0.0

... 1 缺陷试样加载试验Bridgman^[18]设计的缺口圆棒拉伸试验是获取断裂应变与应力三轴度之间关系的一种有效方法 ...

2012

0.0

. 2012, 44(2):246-250 DOI:doi:10.3969/j.issn.1005-2615.2012.02.018

Investigation on local necking of sheet metal forming based on strain-path analysis

板料拉伸失稳时的应变路径分析

Xu Yan , Wang Hui , Wang Juan

徐岩, 王辉, 王娟

摘　要：采用图像识别技术,得到了板料成形试验中极限应变点的成形路径曲线。从成形路径的角度分析了成形极限图的形成,并比较了不同厚度及热处理方式对铝合金LY12塑性变形的影响。将Hill＆MK理论与陈胡理论预测的成形极限及其路径与试验值进行了对比,试验结果表明：在板料失稳时淬火铝板的应变路径没有发生突变,而退火铝板在失效前,会产生一段应变漂移现象。理论与试验结果的对比可以看出,对于这两种铝合金材料来说,Hill＆MK理论预测的成形极限更为接近实验数据。

... 有限元模拟加载过程中,选择缺陷处单元应变路径的改变作为试样断裂的标志^[19] ...

2004

0.0

... 研究表明^{[20, 21]},应力三轴度在材料整个变形过程中是一直变化的,仅获取断裂时刻的应力三轴度不能反映变形过程中三轴度对材料断裂的影响 ...

2004

0.0

... 研究表明^{[20, 21]},应力三轴度在材料整个变形过程中是一直变化的,仅获取断裂时刻的应力三轴度不能反映变形过程中三轴度对材料断裂的影响 ...