引用本文
王贵参, 黄岚, 王岩, 宋立明, 欧歌. 引入极值非相邻连接的连接聚类方法. 2016, 46(5): 1616-1621
WANG Gui-shen, HUANG Lan, WANG Yan, SONG Li-ming, OU Ge. Link clustering method based on maxima and minima non-neighbor link similarity. Journal of Jilin University Engineering and Technology Edition, 2016, 46(5): 1616-1621  
Permissions
Copyright©2016, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
引入极值非相邻连接的连接聚类方法
王贵参1,2, 黄岚1,2, 王岩1,2, 宋立明1,2, 欧歌1,2
1.吉林大学 计算机科学与技术学院,长春130012
2.吉林大学 符号计算与知识工程教育部重点实验室,长春 130012
通信作者:黄岚(1974-), 女, 教授, 博士生导师.研究方向:社会网络与数据挖掘,计算智能.E-mail:huanglan@jlu.edu.cn

作者简介:王贵参(1987-), 男, 博士研究生.研究方向:社会网络与数据挖掘.E-mail:clouddragon2@qq.com

基金:国家自然科学基金项目(61472159, 61572227)
摘要

针对在连接相似度的计算过程中原始连接聚类(LC)方法并未考虑非相邻连接的相似关系,本文提出的极值非相邻连接相似度策略,弥补了原有连接相似度的不足。新的极值非相邻连接相似度(MLS)策略考虑了连接之间相似关系的邻居节点集合的最大、最小情况。在此基础上,结合EQ评估策略,给出了新的引入极值非相邻连接的连接聚类(MLC)方法。在3组测试数据集上的实验结果表明:本文MLC方法相比原始LC、经典重叠社区发现(CPM)方法和扩展的连接聚类ELC方法在多种评估指标上表现优异。

关键词: 人工智能; 连接聚类; 连接相似度; 重叠社区发现; 相邻连接; 非相邻连接
中图分类号:TP301 文献标志码:A 文章编号:1671-5497(2016)05-1616-06
Link clustering method based on maxima and minima non-neighbor link similarity
WANG Gui-shen1,2, HUANG Lan1,2, WANG Yan1,2, SONG Li-ming1,2, OU Ge1,2
1.College of Computer Science and Technology, Jilin University, Changchun 130012, China
2.Key Laboratory of Symbol Computation and Knowledge Engineering,Ministry of Education, Changchun 130012, China
Abstract

Traditional clustering methods can be applied to the research of overlapping community detection directly with link similarity. However, Link Clustering (LC) method does not consider the relationship between non-neighbor links in the calculation of link similarity. In this paper, two link similarity strategies are proposed based on the maxima and minima non-neighbor (MLS) in order to overcome the shortcomings of the original link clustering. The two link similarity strategies consider the minimum and maximum conditions of link similarity relationships. Then, a link clustering method is put forward based on MLS strategies (MLC) with EQ evaluation. Experimental results on three real-world networks show that the proposed MLC method achieves better performance than the original LC method, classical CPM method and Extended Link Clustering (ELC) method under several evaluation criteria.

Keyword: artificial intelligence; link clustering; link similarity; overlapping community detection; neighbor links; non-neighbor links
0 引 言

Palla等[1]于2005年率先揭示了社区间的重叠现象, 提出了重叠社区发现(CPM)方法, 使重叠社区发现迅速成为复杂网络研究中的热门研究方向。CPM方法是用于无向无权图的重叠社区发现算法, 由 k个节点构成的完全连通子图被称为 k连通图, 而相邻的 k连通子图构成了一个 k连通社区, CPM方法本质上是寻找网络中 k连通社区的过程[1]。在重叠社区发现的研究中, 连接聚类方法作为一类新颖方法, 由Evans[2]和Ahn[3]相继分别提出。连接聚类方法能够通过对复杂网络中的连接进行聚类, 从而达到同时考虑节点的层次和重叠关系的目的。而Ahn等[3]提出的连接聚类(Link clustering, LC)方法更是作为此类方法中的代表性方法, 为研究社区重叠问题提供了崭新的视角和思路。2011年, Kalinka[4]发布了连接聚类的R语言软件包Linkcomm, 针对生物网络分析提供了一套实用工具软件。2013年, Xie等[5]将经典的重叠社区发现方法进行了总结。同年, Huang等[6]提出了扩展的连接相似度计算策略(Extended link similarity, ELS), 并且基于该相似度策略提出了一种扩展的连接聚类(Extended link clustering, ELC)方法。之后, Shi等[7]提出了一种使用遗传操作的连接聚类方法。2014年, Lim等[8]将DBScan算法应用于连接社区发现中, 并提出LinkScan算法。同年, He等[9]使用产生式模型和非负矩阵分解的方法, 并将其用于连接社区发现中。由于在重叠社区发现中具有独特的优势, 连接重叠社区发现已成为重叠社区发现研究中的重要课题[5]。与此同时, 社区发现研究的深入也带动了社区发现结果评估的发展。2009年, Shen等[10]提出的拓展的模块度EQ评估已经成为重叠社区发现中的一种重要评估策略。同年, Lancichinetti等[11]提出的ENMI(Extended normalized mutual information)策略是另外一种常用的重叠社区结果评估策略。2010年, Ahn等[3]则使用分割密度(Partition density, PD)策略评估重叠社区效果。

本文针对连接聚类LC方法中连接相似度未考虑非相邻连接的不足, 通过引入连接之间相似程度的邻居节点集合的最大、最小情况, 考虑了非相邻连接之间的相似关系, 提出了引入极值的非相邻连接相似度策略; 进而结合EQ评估, 提出了引入极值的非相邻连接的连接聚类(MLC)方法。在空手道俱乐部、海豚社会网络、美国政治图书等真实的复杂网络的测试中, MLC方法与原始LC方法[3]、经典CPM方法[1]和ELC[6]方法相比, 在多种评估策略上表现优异。

1 连接聚类社区分析

2010年, Ahn等[3]提出了基于连接相似度的连接聚类方法。该方法首先使用连接相似度计算连接与连接之间的相似度, 并得到连接之间的相似度矩阵; 然后, 根据相似度矩阵进行层次聚类; 最后, 对层次聚类得到的树状谱系图使用分割密度评估策略进行层次划分。

定义1[3] 与节点 i之间有连接存在的节点和节点 i自身所构成的集合, 被称为节点 i的邻居节点集合。

连接聚类方法LC的等法流程如下:

输入:社区对应的图 G的节点邻接矩阵。

输出:社区 G的节点重叠社区划分结果。

(1)设图 G中连接的数目为 M, 则根据连接相似度 LS(eik, ejk)生成连接相似度矩阵 S, S的规模为M×M, 其中连接相似度 LS(eik, ejk)定义如下:

LS(eik, ejk)=intersection(i, j)union(i, j)1

式中:intersection(i, j)为节点i和节点j的邻居节点集合的交集; union(i, j)为节点i和节点j的邻居节点集合的并集; eik为节点 i和节点 k间的连接, 对于没有共同节点的连接 eij和 emn, 则 LS(eij, emn)=0。

(2)对得到的连接相似度矩阵 S进行层次聚类, 得到树状谱系图。

(3)针对树状谱系图的层次聚类结果, 使用分割密度策略进行评估, 每层的分割密度定义如下:

PD=∑imi∑imi·mi-ni+1ni(ni-1)/2-(ni-1)2

其中, 每层中每个单独社区i连接的数量记为mi, 节点的数目记为 ni。分割密度公式中分子部分的 mi-ni+1表示社区中实际连接与社区的最小可能发生连接之差, 分母中 ni(ni-1)/2-(ni-1)表示的是社区中最大可能发生连接与最小可能发生连接之差, 而mi/ ∑imi表示第i个社区占所有连接的权重。据此, 可以计算出每个层次的分割密度值。最后根据计算出来的每个层次的分割密度值, 选择PD值最高的层作为最佳的划分层次。

2 引入极值非相邻连接的连接聚类

由原始LC连接相似度计算公式可知, 其在连接相似度上未考虑非相邻连接的情况; 同时, 分割密度公式中, 通常情况下连接的数量 mi远小于点的平方 ni2, 使最终划分指标趋于细小的社区。为此, 本文提出了引入极值非相邻连接的连接聚类方法。

2.1 引入极值非相邻连接的连接相似度(MLS)

定义2 不具有公共节点的两条连接 eij和 emn, 称为非相邻连接。

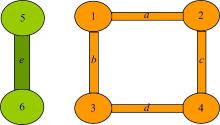
由原始LC方法可知, 对于没有公共节点的连接之间的连接相似度均为0。如图1所示, 对于连接 a和连接 d来说, 直观上属于一个社区, 但是由于 a、d之间没有公共节点, 所以 LS(a, d)=0; 同时, a、d与社区外连接 e之间也不存在公共节点, 因此 LS(a, e)=0, LS(d, e)=0。于是, 从连接相似度的角度来说, 无法有效地区分社区内与社区外非相邻连接之间的关联程度。

图1 示例网络Fig.1 Example network

针对原始连接相似度的不足, 本文将极值非相邻连接引入到连接相似度计算中。与文献[6]中的扩展连接相似度ELS不同, 本文将邻居节点集合的最大最小情况引入到连接相似度策略中, 即MLS(Maxima and minima link similarity), MLSmin和 MLSmax的计算如下:

MLSmin(eij, emn)=intersection(eij, emn)min(eij, emn)3MLSmax(eij, emn)=intersection(eij, emn)max(eij, emn)4式中:intersection(eij, emn)=∑u∈(i, j), v∈(m, n)|intersection(u, v)|min(eij, emn)=∑u∈(i, j), v∈(m, n)|min(u, v)|max(eij, emn)=∑u∈(i, j), v∈(m, n)|max(u, v)|

u和 v表示节点, 两种新的极值非相邻连接相似度均考虑了没有共同节点连接之间的相似度。 intersection(u, v)表示节点 u和 v的共同邻居节点集合, min(u, v)表示节点u和v的邻居节点集合中元素数目的较小者, max(u, v)表示节点u和v的邻居节点集合中元素数目的较大者, |· |表示集合中元素的数目, 本文采用的是与连接聚类LC方法相同的邻居节点集合方式, 即节点的邻居节点集合中包括节点自身。

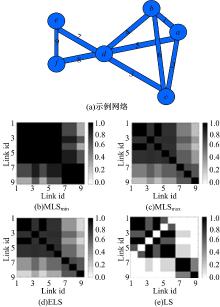
本文考虑两条连接中4个节点的邻居节点集合的最小数目和最大数目, 是连接的拓扑结构的两种极值情况。而这两种方式的改变, 会导致社区发现的不同。极值非相邻连接相似度MLS与原始连接相似度LS之间的比较如图2所示, 该网络包括6个节点和9条连接。从图2(b)~(e)所示的相似度矩阵的密度图中可以看出, 两种新的极值非相邻连接相似度的相似度矩阵都比原始的连接相似度矩阵稠密, 使得示例网络(见图2(a))聚类划分更为清晰。

图2 基于示例网络的相似度矩阵Fig.2 Similarity matrix based on example network

2.2 引入模块度策略EQ的结果划分

由式(2)可知, 原始分割密度PD策略在对社区进行划分时, 随着社区中连接的增长, ni(ni-1)/2-(ni-1)的增加的速度比 mi-ni+1的增加的速度快, 因为通常来说, 社区中边的增长速度是达不到节点的平方 O(n2)级别的。随着节点数目的增多和连接数量的增加, 分割密度值会变小, 因此分割密度倾向于将网络划分为较小的社区。而这种较小的社区与真实网络社区之间将产生一定差距, 于是本文采用与文献[6]相同的方法, 引入EQ策略替代PD评估策略进行层次划分。

Shen等[10]在2009年提出了改进的EQ策略, 并将改进的模块度EQ这一概念应用于重叠社区发现评估上, 公式如下:

EQ=12m∑i∑v∈Ci, w∈Ci1OvOwAvw-kvkw2m5

式中: Ci为网络划分后的由节点i构成的社区; m为整个网络的连接数目之和; Ov、Ow为节点 v、w属于不同社区的数目; Avw表示节点 v和节点 w之间是否有连接存在, 若有则为之间是否有连接存在, 若有则为1, 否则为0; kv、kw表示节点 v、w的度; EQ值越接近1, 表示模块性越好, 并且暗示着可能会出现重要的重叠社区结构。

本文采用的EQ与文献[6]中的不同之处在于, 文献[6]中采用的EQ是在无向无权图中, 节点 v到 w以及节点 w到 v这两种情况仅计算一次, 且未考虑节点 v等于节点 w的情况, 其结果接近本文EQ值的1/2。

2.3 基于MLS和EQ的连接聚类(MLC)方法

引入极值非相邻连接的连接聚类MLCmin和MLCmax的MLC方法流程如下。

输入:社区对应的图 G的节点邻接矩阵。

输出:社区 G的节点重叠社区划分结果。

(1)设图 G中连接数目为 M, 根据MLSmin和MLSmax公式计算相应的连接相似度, 并生成连接相似度矩阵 S, S的规模为 M×M。

(2)对连接相似度矩阵 S进行层次聚类, 得到树状谱系图。

(3)针对树状谱系图的层次聚类结果, 使用EQ策略进行评估, 选择EQ值最高的层作为最佳的划分层次。

3 实 验

在空手道、海豚、政治图书3个测试数据集上, 将MLC方法在社区分类数目(Community number, CN)、EQ、ENMI三个评估策略上与原始LC方法、经典的CPM方法以及ELC方法进行对比。

3.1 实验数据集

本文算法采用的数据集如表1所示, 包括空手道数据集(Karate)、海豚数据集(Dolphin)和政治图书数据集(Political), 这3个数据集都是重叠社区发现研究中经常使用的数据集[5], 这3个数据集的标准划分分别为2、2、3个社区。

表1 数据集概况 Table 1 Survey of datasets
3.2 实验结果评价策略

在实验结果评估上, 本文使用了社区分类数目CN、EQ和ENMI三个评估策略。其中, 社区分类数目CN指的就是算法最终得到的社区分类数目; ENMI策略则是由Lancichinetti等人提出的[11]。ENMI以互信息作为评估基础, 需要预先知道接近真实分类的标准划分结果。

3.3 算法效果分析

针对空手道(Karate)、海豚(Dolphin)和政治图书(Political)3个数据集将本文MLC方法与原始LC、经典的CPM和ELC方法进行了横向比较。3个数据集的网络拓扑结构图, 以及在4种方法下对应的树状谱系图和分类决策图如图3所示, 对应的CN、ENMI和EQ评估效果如表2所示。根据表2的实验结果可以看出, 在空手道数据集中, MLCmin方法和ELC方法均得到了与标准划分相同的社区数目, 但是MLCmin方法具有最高的ENMI值。MLCmax方法得到了最高的EQ值, 而社区数目与标准划分略有不同。ELC方法获得了与标准划分相同的社区数目, 并且与MLCmin和MLCmax方法的结果比较接近。相比之下, LC方法与标准划分的社区数目相差较多, CPM方法得到的结果中有一个包括25个节点的大社区, 这两种方法与真实情况相比都有很大差异。在海豚数据集中, ELC方法取得了最优结果, 和标准划分的社区数目相同, MLCmin方法取得了次优结果, 在EQ值上与ELC方法相比仅差0.02。而MLCmax与CPM方法的结果较为接近。LC方法得到了13个社区, 这与标准划分的3个社区结果相差甚远。在政治图书数据集中, MLCmin方法得到了与标准划分相同的社区数目和最高的EQ值, ELC方法得到了最高的ENMI值, 但与MLCmin方法的ENMI值相差不多。LC方法得到了32个社区, 这与标准划分的3个社区结果相比存在很大差异。尽管CPM方法也得到了最高的EQ值, 但与同样具有最高EQ值的MLCmin方法相比, 后者获得了与标准划分相同的社区数目。因此, 在综合考虑3个评估策略的情况下, MLCmin方法的效果是最理想的。总体来说, MLC方法表现优异。

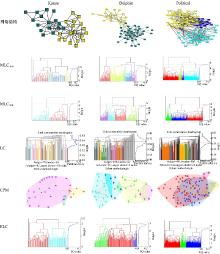图3 数据集的网络结构及树状谱系图和分类决策图Fig.3 Network topological and classifying decision graph, dendrogram of the datasets

表2 数据集的实验结果 Table 2 Result table of the datasets
4 结束语

本文对于重叠社区发现问题提出了引入极值非相邻连接的连接聚类方法(MLC), 在MLCmin和MLCmax两种极值非相邻连接相似度基础上, 结合EQ评估来弥补原始连接聚类方法的不足。在3个真实的复杂网络测试中, 与原始的LC、经典的CPM和ELC方法进行比较, 引入极值非相邻连接的连接聚类方法(MLC)在多个评估策略下表现优异。对于大规模复杂网络中的重叠社区分析及动态复杂网络分析, 将是进一步需要深入研究的内容。

The authors have declared that no competing interests exist.

参考文献
[1] Palla G, Derényi I, Farkas I, et al. Uncovering the overlapping community structure of complex networks in nature and society[J]. Nature, 2005, 435(7043): 814-818. [本文引用:3]
[2] Evans T S, Lambiotte R. Line graphs, link partitions, and overlapping communities[J]. Phys Rev E, 2009, 80: 016105. [本文引用:1]
[3] Ahn Y Y, Bagrow J P, Lehmann S. Link communities reveal multi-scale complexity in networks[J]. Nature, 2010, 466(7307): 761-764. [本文引用:6]
[4] Kalinka A T. The generation, visualization, and analysis of link communities in arbitrary networks with the R package linkcomm[J]. Bioinformatics, 2011, 27(14): 2011-2012. [本文引用:1]
[5] Xie J R, Kelley S, Szymanski B K. Overlapping community detection in networks: the state-of-the-art and comparative study[J]. ACM Comput Surv, 2013, 45(4): 43. [本文引用:3]
[6] Huang L, Wang G, Wang Y, et al. Link clustering with extended link similarity and EQ evaluation division[J]. PloS One, 2013, 8(6): e66005. [本文引用:6]
[7] Shi C, Cai Y, Fu D, et al. A link clustering based overlapping community detection algorithm[J]. Data & Knowledge Engineering, 2013, 87: 394-404. [本文引用:1]
[8] Lim S, Ryu S, Kwon S, et al. LinkSCAN*: overlapping community detection using the link-space transformation[C]∥2014 IEEE 30th International Conference on Data Engineering, Chicago, IL, 2014: 292-303. [本文引用:1]
[9] He D, Jin D, Baquero C, et al. Link community detection using generative model and nonnegative matrix factorization[J]. PloS One, 2014, 9(1): e86899. [本文引用:1]
[10] Shen Hua-wei, Cheng Xue-qi, Cai Kai, et al. Detect overlapping and hierarchical community structure in networks[J]. Physica A: Statistical Mechanics and its Applications, 2009, 388(8): 1706-1712. [本文引用:2]
[11] Lancichinetti A, Fortunato S, Kertész J. Detecting the overlapping and hierarchical community structure in complex networks[J]. New Journal of Physics, 2009, 11: 033015. [本文引用:2]
[12] Zachary W W. An information flow model for conflict and fission in small groups[J]. Journal of Anthropological Research, 1977, 33(4): 452-473. [本文引用:1]
[13] Lusseau D, Schneider K, Boisseau O J, et al. The bottlenose dolphin community of doubtful sound features a large proportion of long-lasting associations[J]. Behavioral Ecology and Sociobiology, 2003, 54: 396-405. [本文引用:1]
[14] Newman M E J. Modularity and community structure in networks[J]. Proc Natl Acad Sci, 2006, 103(23): 8577-8582. [本文引用:1]
[15] Newman M. Network collection from Newman M[EB/OL]. [2015-11-12]. http://www.cise.ufl.edu/research/sparse/matrices/Newman/polbooks.html. [本文引用:1]