约束满足问题(Constraint satisfaction problem, CSP)^[1]是人工智能领域的一个重要研究方向。作为一种抽象模型, 约束满足问题可以对现实世界中的很多问题进行建模求解, 被广泛应用于调度、规划、网络以及生物信息学等诸多领域, 得到了越来越多的重视和研究。求一个约束满足问题的解或者证明其无解都是NP-hard问题^[1], 所以提高约束满足问题求解效率一直是该领域研究的热点。求解约束满足问题一般采用约束推理技术与智能搜索相结合的方式:约束推理技术如相容性技术^[2]等可以对约束网络进行剪枝以控制问题的求解规模; 智能搜索如启发式方法^[3]等可以指导问题的求解顺序, 使问题能够尽早地求出解或者得出无解的结论。目前应用比较广泛的CSP求解算法就是嵌入了约束传播技术和启发式策略的回溯算法^{[2, 3]}。

研究人员已经提出了多种多样的推理技术以提高约束满足问题的求解效率, 而基于冲突的约束推理技术是其中比较有代表性并且取得良好效果的一种。目前比较通用、效果比较突出的基于冲突的约束推理技术包括Nogood方法^[4]、基于状态的检索策略(State-based search)^[5]以及基于上一次冲突的推理技术(Last-conflict based reasoning, LC)^[6]等。本文在研究基于冲突的约束推理技术的基础上, 对LC方法进行了进一步的扩展。因为LC方法只关注了搜索过程遭遇冲突时应该如何回溯, 作者在其基础上更进一步发现, LC方法回溯并实例化成功时, 其当前回溯层变量是造成上一次冲突的必要组成成分, 根据变量顺序启发式的失败优先原则, 应该优先选择该变量进行实例化。基于此, 本文提出了基于成功回溯的约束推理技术及其相应的MAC_BTS算法, 并通过国际通用的Benchmark用例进行了测试, 实验结果表明本文提出的基于成功回溯的约束推理技术比单纯的LC方法有更进一步的效率提升。

定义1(约束满足问题(Constraint satisfaction problem, CSP)^[1]) 一个约束满足问题 P可表示为一个三元组 P=< X, D, C>其中, X={X1, X2, …, Xn}为一个有限的变量集合; D={D1, D2, …, Dn}为对应变量的有限论域集, Di∈D对应 Xi∈X; C={C1, C, …, Ck}为一个有限的约束集合, 任意 Cj∈C表示变量取值之间的制约关系。

约束满足问题可以根据约束中包含的变量个数分为二元约束满足问题和多元约束满足问题, 其中, 多元约束满足问题可以转化为等价的二元约束满足问题, 因此, 二元约束满足问题一直是该领域研究的热点。本文主要讨论二元约束满足问题。一个约束满足问题的解是对每个变量 Xi∈X进行赋值, 即令 Xi=ai, 其中 ai∈dom(Xi),如果每个变量都被实例化后, 所有约束都能被满足, 则称该实例化集合为该约束满足问题的一个解; 如果不存在实例化集合使得所有约束都被满足, 则称该问题是不可满足的。

定义2(弧相容(Arc consistency, AC)^[7]) ①一个值 (X, a)是弧相容的, 当且仅当在每一个包含 X的约束 C中都存在 (X, a)的支持; ②一个变量X是弧相容的, 当且仅当 ∀a∈dom(X), (X, a)是弧相容的; ③一个约束网络是弧相容的, 当且仅当该网络的每一个变量都是弧相容的。

维持弧相容(Maintaining arc consistency, MAC)^[8]算法是被公认为求解CSP问题效率最优的通用完备方法。MAC算法是在回溯算法框架内嵌入AC算法, 在搜索过程中维持弧相容的状态, 每实例化一个变量, 利用AC算法进行约束传播, 如果得到的约束网络仍然是弧相容的, 则实例化成功; 否则, 发生回溯。

算法1 MAC算法^[8]

1. mac(CSP P=(X, D, C))

2. begin

3. P← AC_consistency(P);

4. if P=⊥ then

5. return false;

6. if ∀ X∈ P, |dom(X)|=1 then

7. return true;

8. X← selectVariable(P);

9. a← selectValue(X);

10. if AC(P|X=a) then

11. return mac(P|X=a);

12. else

13. return mac(P|X≠ a);

14. end

定义3(Nogood集合^[4]) 如果约束网络经过一个指派序列Δ 实例化后得到的网络不可满足, 则称Δ 是Nogood集合。

约束求解过程中, 如果选择变量 Xi实例化失败是因为变量 Xi与已实例化变量集 {X1, X2, …, Xk}之间存在冲突, 此时MAC算法需要向搜索树的上一层回溯。根据LC方法的思想, 变量 Xi有比较大的可能性是与已实例化变量集的某个子集存在冲突, 即变量 Xk可能不是Nogood的必要组成成分, 所以回溯到变量 Xk层后仍然优先实例化变量 Xi。

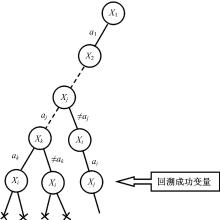
如图1所示, 回溯到变量 Xk层后, 实例化变量 Xi仍然失败, 说明变量 Xk确实不是Nogood的必要组成成分, 即此时变量 Xi与已实例化集合 {X1, X2, …, Xk-1}仍然不相容。接着向上层回溯, 如此反复, 直到回溯到变量 Xj层时实例化变量 Xi成功, 然后使用变量启发式选取变量进行实例化。这里可以看到:①LC方法在回溯到变量 Xj之前的所有实例化变量 Xi的尝试都以失败告终, 说明了变量集 {Xj+1, …, Xk}不是造成冲突的原因, LC方法避免了对这些变量的扩展, 起到了剪枝的效果; ②LC方法在回溯到变量 Xj时实例化变量 Xi成功, 说明了变量 Xj是造成前述冲突的原因, 即变量 Xj是Nogood的必要组成成分, 而因为回溯后破坏了这个必要组成成分, 才使得变量 Xi可以实例化成功, 据此得出定理1。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 LC方法示意图Fig.1 Schematic diagram of last-conflict based reasoning

定理1 如果LC方法在回溯到变量 Xj时能够成功实例化, 则变量 Xj是Nogood的必要组成成分。

定义4(回溯无效变量) LC方法在实例化变量 Xi时遭遇冲突并回溯, 如果回溯到变量 Xk后, 无论变量 Xi实例化为何值, 约束网络都不相容, 则称变量 Xk为回溯无效变量。

回溯无效变量的特点是这些变量不是造成变量 Xi实例化失败的原因, 即无论回溯无效变量实例化为何值或者不管其是否实例化, 都不会影响变量 Xi的实例化结果。LC方法正是通过优先对变量 Xi进行实例化, 避免了对回溯无效变量的扩展, 起到了剪枝的效果。

定义5(回溯成功变量) LC方法在实例化变量 Xi时遭遇冲突并回溯, 如果回溯到变量 Xj时, 变量 Xi实例化成功, 则称变量 Xj为回溯成功变量。

根据定理1, 回溯成功变量 Xj是Nogood的必要组成成分。既然回溯成功变量 Xj是造成变量 Xi实例化失败的原因, 那么在成功实例化变量 Xi后重构该冲突集合, 根据冲突的双向性, 变量 Xi实例化后得到的已实例化变量集与回溯成功变量 Xj存在冲突的可能性非常大。根据变量顺序启发式的失败优先原则, 此时应该选择回溯成功变量进行实例化。据此, 本文提出了基于成功回溯的约束推理技术。

定义6(基于成功回溯的约束推理技术) LC方法在遭遇冲突时回溯并实例化成功后, 优先选择当前回溯成功变量进行实例化的约束推理方法。

将基于成功回溯的约束推理技术应用于MAC算法中, 本文给出了算法MAC_BTS, 其示意图如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 MAC_BTS示意图Fig.2 Schematic diagram of MAC_BTS's

定理2 算法MAC_BTS在一条分支上回溯到网络相容状态的最坏时间复杂度是 O(ned3)。其中, n为节点数, e为约束个数, d为最大论域大小。

证明 约束满足问题在利用MAC_BTS算法进行求解时, 其搜索树的一条分支上最多扩展了 n个节点。当算法遭遇冲突时, MAC_BTS算法需要在算法1中第8行应用基于成功回溯的约束推理技术来选择变量, 在算法1中第9行选取适当的值进行实例化, 并在算法1中第10行检查实例化之后的网络相容性。在最坏情况下每次回溯后的实例化都没有成功, 即最多需要检查冲突变量 Xi中论域中的所有值 n次, 共需要 nd次相容性检查。因为时间最优的相容性检查算法的时间复杂度为 O(ed2),如果算法MAC_BTS使用时间最优的相容性算法, 则整个求解过程的时间复杂度是 O(ned3)。

采用目前国际上主流的MAC3rm算法^[9]作为基本求解算法。其中, 基本的MAC算法单纯使用Dom/Wdeg变量启发式^[10]; MAC_LC算法使用Dom/Wdeg变量启发式以及LC方法; MAC_BTS算法使用Dom/Wdeg变量启发式以及LC方法, 并加入了基于成功回溯的约束推理技术。实验以求解所消耗的CPU耗时和检索过程生成的节点数作为参考标准, 其中CPU时间以ms为单位, 生成节点数记为Nodes。测试环境为Intel Core2 Duo CPU E7500 2.93 GHz。

因为LC方法以及MAC_BTS立足的出发点是冲突的产生是由于当前实例化变量与已实例化变量集的某个子集存在冲突, 该出发点要求问题有一定的结构才能出现明显的效果, 从而使得LC方法以及MAC_BTS算法能够起到积极的作用。而随机问题^[11]是个平均问题, 即不同的变量有着相同的论域和约束关系, 基本上很少存在或者不存在当前实例化变量与已实例化变量集的某个子集存在冲突的情况, 所以LC方法以及MAC_BTS算法在随机问题上不仅没有起到积极作用, 反而会阻挠启发式的工作, 增加了不必要的分枝扩展。所以本实验部分只对Benchmark问题进行测试并分析, 本文选取的测试用例XML描述文档可从文献[12]在线下载。

实验选取了多种类型问题的测试用例进行了对比, 并选取有代表性的问题实验结果列举在表1中。为了避免单个问题本身的结构特性对结果造成影响, 本文对同一组问题的多个实例的测试结果取平均值进行比较。

表1

Table 1

表1(Table 1)

表1 求解实际问题对比 Table 1 Comparison of solving real-world instances Instances Index MAC MAC_LC MAC_BTS BH-4-4 耗时/ms 575 824 741 节点数 6293 8750 7217 bqwh15_106 耗时/ms 174.9 212.3 199 节点数 1633 1876 1862 coloring 耗时/ms 10041 6747 6047 节点数 177000 131000 99000 composed-2 5-10-20 耗时/ms 43.8 32.6 32 节点数 504.7 377 392 composed-7 5-1-25 耗时/ms 33 28 25 节点数 338.9 264.5 253 composed-7 5-1-80 耗时/ms 20.4 15.7 15.3 节点数 147.3 100 100 driver 耗时/ms 16600 14300 13500 节点数 3025 2291 2064 ehi-90 耗时/ms 1343.4 164 210 节点数 1054 142 143 fapp02 耗时/ms 1194.6 460 463 节点数 406.9 284.3 296 frb30-15 耗时/ms 493.8 797 1223 节点数 3317 4933 5675 js-enddr1 耗时/ms 2700 3400 3000 节点数 25000 28000 24000 QCP-10 耗时/ms 17.7 15.5 17.8 节点数 173.3 156.4 165 QWH-10 耗时/ms 18.7 20.4 16 节点数 205.5 215.2 192

表1 求解实际问题对比 Table 1 Comparison of solving real-world instances

由表1可以看出, MAC_BTS方法在绝大多数情况下都比LC方法有进一步的提高。这是因为二者的理论基础相同, 如果当前实例化变量与已实例化变量集的开始部分的子集有冲突, LC方法就能够避免许多回溯无效变量的扩展, 从而提高求解效率, 而此时MAC_BTS方法在LC方法的基础上, 在上一次冲突变量实例化成功后立即选择回溯成功变量进行实例化, 从而重新构造了冲突的可能性, 尽早地向更高层回溯, 进一步提高了求解效率。

基于成功回溯的约束推理技术适用于LC方法, 是因为两者的理论基础相同, 在LC方法起作用时, 基于成功回溯的约束推理技术能更进一步地提高问题的求解效率。但是对于单纯的MAC方法来说, 在遭遇冲突回溯后选择的变量不一定是刚才实例化失败的变量, 即使回溯后实例化成功了, 也无法说明此时的回溯成功变量是Nogood的必要组成成分。如果MAC方法遭遇冲突后选择的变量不是上一次冲突的变量, 回溯成功后应用基于成功回溯的约束推理技术选择回溯成功变量进行实例化, 其实只是额外地扩展了一个回溯无效变量, 从而使得求解空间更加复杂, 而没有起到预期的尽早构造冲突的效果。所以, 基于成功回溯的约束推理技术不一定适用于单纯MAC方法, 却适用于LC方法, 对LC方法有着进一步的问题求解效率提升。

在详细分析了LC方法原理的基础上, 指出了LC方法起作用的本质是剪掉了部分回溯无效变量的搜索分枝, 从而避免了在无效分枝上的冗余操作, 并得出了回溯成功变量是Nogood必要组成成分的结论。根据该结论, 本文对LC方法进行了进一步扩展, 即在LC方法回溯并实例化成功后优先选择回溯成功变量进行实例化, 从而重构了上一次冲突的变量集, 此时有较大的冲突可能性, 符合变量顺序启发式的失败优先原则。基于此, 提出了基于成功回溯的约束推理技术及其相应的MAC_BTS算法, 最后通过实验与LC方法进行了对比, 实验结果表明, 基于成功回溯的约束推理技术确实比单纯的LC方法有更进一步的效率提升。