图像上的少数特殊点能在保留图像图形重要特征的同时, 有效地减少信息的数据量, 提高计算的速度, 有利于图像的可靠匹配, 角点便是这类点的代表。但角点是二维图像变化剧烈的点或是图像边缘曲线上曲率极大值的点, 所以在生成角点的同时, 会忽略很多信息含量很高的点, 额外引入一些在数学计算上特殊的点, 而非具有实际意义的点。基于此, 本文提出了一种新型的“ 特殊” 点— — 类特征点。

类特征点不是通过单幅形状计算得到, 而是通过统计的方式得到。将数据库中同一类的一组形状提取轮廓特征点, 用特征点匹配的方式进行交叉匹配, 记录每个形状上匹配成功次数超过一定阈值的特征点, 把这些点作为该形状的类特征点。具体算法如下:

算法1 类特征点

给定一个带类标签的数据库D:

1.对于D中每一个形状 S,提取其特征点, 并保存每个特征点的坐标及其他相关数据, 针对每个特征点设置一个值c=0。

2.对于数据库D中每个具有同一类标签的形状集P={S₁, S₂, …, S_n}进行交叉匹配(本文采用SC中的特征点匹配算法)。

3.对于每对进行匹配的形状S_i, S_j(∀ i, j∈ [1, 2, …, n], i≠ j)

For each point x∈ S_i

If x获得匹配

c=c+1

End_If

End_For

4.根据阈值θ 的不同, 便可以将特征点分为类特征点(c> θ ), 非类特征点(c≤ θ )

通过算法1可提取数据库中每个形状的类特征点, 效果见图1, 其中十字是形状轮廓点, 圆圈是训练得到的类特征点。从效果图中可以看出, 这些类特征点很好地还原了形状本身, 相对于角点具有更好的代表性。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 类特征点效果图Fig.1 Example of class-points

类特征点的提出不仅为形状找到了一种比角点更可靠的特殊点, 而且对本文接下来提出的融合框架起到核心作用。在类特征点参与下, 本文将在形状匹配的过程中提取出另一种非常重要的特征点— — 形变特征点。

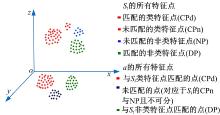
通过上述统计方式, 统计数据库中所有形状, 将其轮廓上的特征点划分为类特征点和非类特征点, 对于常见的检索实验:当待检索的形状 a与数据库中的形状 Si(i=1, 2, …, n)进行匹配时, 会将双方的特征点划分为匹配的与未匹配的, 加上之前对数据库进行的预处理, 进而产生如图2的结果。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 不同种类的点Fig.2 Points of different types

本文将匹配的非类特征点(DP)称为形变特征点, 因为它代表了形状发生轻微变形的那些区域。从图2中可知, 当前进行匹配的数据库形状 Si的特征点被分为4种点, 而对于待检索形状 a, 因为它未被训练生成类特征点, 所以在其未与 Si匹配的点中无法分辨出哪些点对应 Si的未匹配类特征点, 哪些对应 Si的未匹配非类特征点, 因此它们将被统一看作未匹配的点。

所谓未匹配的点, 即在一次匹配过程中并未获得匹配的对应特征点, 两个形状越是相近, 则未匹配的点越少; 差异越大, 则未匹配的点越多。同时, 这些未匹配点的特征代价也会随着形状间的差异而不同, 形状越是相似, 这些点的特征代价越小, 越是不同, 特征代价越大。

至此, 两个形状上的特征点被划分为对应的三类:匹配的类特征点, 未匹配的点, 形变特征点。

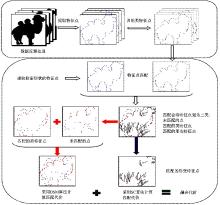
本文提出的融合框架的整体流程如图3所示。匹配类特征点与未匹配的点构成的点集类似形状的刚性结构, 而形变特征点构成的点集类似形状的柔性结构。在匹配的两个形状柔性结构相似的情况下, 刚性结构能更好地表达类外相异性, 而在刚性结构相似的情况下, 柔性结构可以表达类内相似性。若能利用这两种不同结构的特性, 结合全局算法与局部算法的优势, 既能保证效果得到提升, 又能弥补二者的不足。为此, 本文为这两种结构选择了不同的算法来适应它们的特性。对于刚性结构, 采用BSM算法作为一种高效的全局算法, 其刚性网格的结构在处理刚性结构时被证明是有效且高效的手段。而对于柔性结构, SC算法作为一种有着众多改进的经典算法, 其采用的薄板样条模型(TPS)和粗直方图的统计方式, 能够更好地处理形变内容。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 融合框架的流程图Fig.3 Flow chart of fusion framework

在本文提出的框架下, 形变特征点的数量相对稳定, 其特征代价值的大小会刻画类内相似性。而总体数量同样稳定的匹配类特征点和未匹配点, 二者数量之间的此消彼长及特征代价值之间的对应改变会很好地刻画类外相异性。

BSM和SC这两种算法产生的形状特征直方图进行匹配时均可采用卡方系数:

dchi-squareH1, H2=∑iH1i-H2i2H1i+H2i1

式中: H1(i)和H2(i)为进行匹配的两个直方图; d_chi-square(H₁, H₂)为这两个直方图的匹配程度, 值介于0~2之间, 数值越小代表两个直方图越相近。

根据卡方系数, 这两种算法产生的匹配代价可以用如下公式进行计算:

Cost=12∑iH1i-H2i2H1i+H2i2

式中: Cost为BSM或SC算法的特征代价。对于BSM, Cost代表由特征点构建的模糊形状模型的整体代价; 对于SC, Cost代表经过标准化后的特征点特征代价总和。虽然二者产生特征代价的数据模型不同, 但是可以通过卡方系数将二者分别产生的特征代价量化为0~1的常量。

总的融合代价将根据对应点数的不同采取加权统计的方式(见式(3))进行融合, 根据融合代价值来衡量两个形状的相似性, 代价越低, 越相似。实验证明这种融合方式具有良好的效果和一定的扩展性。

FusionCost=num_PointsMethod_Anum_TotalPoints×CostA+num_PointsMethod_Bnum_TotalPoints×CostB3

式中:num_Points_{Method_A}、num_Points_{Method_B}分别为采用方法A和方法B的特征点数量; num_TotalPoints为总的特征点数量; Cost_A、Cost_B分别为方法A和方法B产生的匹配代价值。

为验证本文算法框架的有效性, 选取了MPEG-7数据库^[17]进行实验。该数据库有1400个样本, 包含70个类别各20个形状。分别利用BSM、SC及本文提出的FBS(Fusion framework of BSM and SC)对MPEG-7中的数据样本进行靶心率测试, 该测试对数据库中的每一个形状进行检索, 计算在前40个最相近的结果中有多少个形状与检索形状是同一类别, 这个比值作为该形状的检索率, 而所有形状的检索率的平均值将代表整个数据库的检索率。

在该测试中, 为了验证本文框架的有效性, 对测试环境做了精简, 消除了一些优化方法对实验结果带来的影响, 仅对每个形状提取100个特征点, 并添加垂直和水平翻转预处理。对于BSM, 采用文献[17]推荐的16× 16个网格, 对于SC采用文献[9]中的朴素形状上下文距离D_sc, 而FBS将基于二者所采用的参数进行融合, 其中阈值 θ为0.85。本文方法(FBS)与BSM和SC对相同数据在上述条件下进行实验检索精度的结果分别为68.31%、62.13%和66.84%。可以看出, FBS框架对融合的两种算法均有不同程度的提升。

对Kimia-99形状数据库^[18]进行了测试, Kimia-99数据库包含了9个类别各11个形状。对数据库中的每一个形状进行检索, 并将结果排序, 取排名前十的形状(Top-10), 统计这10个形状是否属于测试形状所属类。因为数据库中共有99个形状, 所以对于Top-N, 最佳的结果便是99。表1显示了本文融合算法与BSM和SC对相同数据进行实验的结果比较。

表1

Table 1

表1(Table 1)

表1 Kimia-99数据库的检索结果 Table 1 Retrieval results on Kimia-99 data set 方法 1st 2nd 3rd 4th 5th 6th 7th 8th 9th 10th 全部 BSM[17] 99 97 90 86 78 70 69 64 58 48 759 SC[9] 97 91 88 85 84 77 75 66 56 37 756 FBS 99 97 91 91 83 78 65 67 54 55 780

表1 Kimia-99数据库的检索结果 Table 1 Retrieval results on Kimia-99 data set