自然界与现实世界的复杂系统都可以用复杂网络来描述其结构, 例如基因调控网、流行病传播网、互联网、各种形式的社交网络、社会系统、生物系统。复杂网络自身具有无标度^[1]、小世界^[2]和分形特性^[3]。无标度特性反映复杂网络中节点的度呈现出幂律分布特征。小世界特性反映复杂网络的高聚类系数和短路径长度的特征。分形特性反映了复杂网络的自相似特征。近几年, 随着复杂网络理论应用的快速发展, 复杂网络逐渐引起人们的重视, 网络结构与网络功能的关系日益成为研究的热点, 吸引了计算机、生物、物理、社会学等方面学者不断投入到此项工作中。社区结构作为复杂网络的重要结构特征, 已经成为多学科交叉研究领域的焦点之一。

社区是一个内部节点间连接紧密的节点集合, 而它与网络其他部分连接稀疏。已有网络社区检测方法可以分为三类:第一类是基于优化的方法, 典型算法有Newman等^{[4, 5]}提出的GN和FN方法, Barber等^[6]提出的LPAm方法, 郭玉泉等^[7]提出的启发式遗传算法; 第二类是层次聚类方法, 典型算法有沈华伟等^[8]提出的EAGLE方法、Palla等^[9]的CPM方法; 第三类是网络动力学方法, 典型算法有Jin等^[10]提出的基于马尔可夫方法的社区检测方法。这三类方法都直接或间接利用了复杂网络的幂律分布特征, 即从网络中具有度较高的节点开始检测社区结构。虽然上述算法可以有效地检测出社区结构, 但由于是以节点度的幂律分布为基础, 因此社区结构与网络演化的关系并没有明确体现出来。

为评估各种算法社区检测结果的优劣, 2004年Newman^[11]提出了网络社区的度量标准, 称为模块化函数, 又称为 Q函数。虽然它存在分辨率限制的缺点, 但目前它仍然是应用最广泛的社区评价指标。

2007年Gallos等^[12]发现了复杂网络的分形特性, 进一步的研究表明分形的起源是由于网络中心节点的互斥性造成的。其后对复杂网络分形的研究逐渐形成以盒子覆盖法为基础的几何方法和以谱分析为代表的代数方法^[13]。现有的盒子覆盖法只考虑了节点间拓扑距离而忽略了节点间权重, 为此本文提出了两阶段盒子覆盖法解决此问题。以两阶段盒子覆盖法为基础, 进一步提出FCUC(Fractal cluster for uncovering community)方法。方法核心思想是通过两阶段盒子覆盖法完成分形聚类过程^{[14, 15]}, 并且在分形聚类过程中形成分形树, 最后通过对分形树进行分割得到复杂网络的社区结构。这种分割是以 Q函数最大的分割方案作为社区检测结果。分形树不但反映了节点间紧密的程度, 也体现了网络的演化过程。

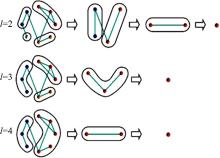
复杂网络分形是一个归一化过程, 图1说明了此过程。通过盒子覆盖法^[16]可以实现这一过程。盒子是一个节点的集合, 并且盒子内任意两节点的距离小于等于 l(l为盒子的直径)。盒子覆盖法将网络节点用若干个盒子覆盖。归一化过程将由若干节点构成的盒子抽象为一个新节点, 盒子间的边作为抽象后节点之间边, 因此每次应用盒子覆盖法就是对网络中节点进行聚类的过程。对一个网络反复应用盒子覆盖法, 网络最终会被聚类为一个节点。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 复杂网络的分形特征Fig.1 Fractal feature of complex networks

常见的盒子覆盖法^[17]分为燃烧法和贪心涂色法两大类。对复杂网络的归一化过程进一步观察可以发现, 目前盒子覆盖方法存在一些不足。首先, 盒子覆盖法没有考虑边的权重, 始终把网络看作无权重网络, 这样单一考虑几何空间距离的方式丢失了盒子之间边权重的拓扑信息。其次, 盒子覆盖法随机选取节点放入到盒子中, 并没有考虑节点是否适合放在当前的盒子中。而最佳的节点放置方案是将节点放入最优盒子中, 同理, 一个好的盒子也一定是容纳节点多的盒子, 而且节点间连接紧密, 即保证每个节点被划入到结合最紧密的盒子中。针对盒子覆盖法以上两点不足, 本文对盒子进行了重新定义, 同时提出了两阶段盒子覆盖法。

定义1 设 B是节点集合, W(a, b)为连接相邻节点 a与 b之间边的权重, 则节点 n与 B的连接度 C定义如下:

C(n, B)=∑b∈BW(n, b)(1)

定义2 盒子是一个节点集合, 节点间边的权重相等, 且任意两节点间距离小于 l(l≥1), 盒子中节点 n与所在盒子 B的连接度 C(n, B)值最大。

根据定义2可知, 一个未指定到任何盒子的节点与某个盒子中的其他节点构成完全子图时, 节点具有最大的 C值。基于上述定义作者提出两阶段盒子覆盖法, 该算法是将盒子覆盖过程分为两个阶段, 第一个阶段将具有完全子图结构的盒子都找到, 第二阶段将第一阶段剩余节点划分到新盒子中。两阶段盒子覆盖法(TSBCA)的详细描述如下:

算法1 两阶段盒子覆盖法

Input

NodeSet1 //节点集合, 初始为网络所有节点;

NodeSet2 //存储第二阶段节点, 初始为空;

Output

Box //输出盒子列表

Begin

1. While NodeSet1 ≠ Ø

2. Begin

3. 在NodeSet1中选择节点n作为种子节点;

4. 计算节点n的边权重相等的最大完全子图SG;

5. If SG中每个阶段不存在一个更大的完全子图

6. 将SG节点作为一个盒子加入Box列表中;

7. 将SG节点从NodeSet1中删除;

8. Else

9. 将节点n放入到NodeSet2中

10. 将节点n从NodeSet1中删除;

11. End if

12. End

13. While NodeSet2≠ Ø

14. Begin

15. 在NodeSet2中随机选择一个节点n;

16. 计算n在NodeSet2中的邻居节点集合N;

17. If N=Ø

18. 将n做为盒子中并加入到Box中;

19. 将n从NodeSet2中移除;

20. Else

21. 在N中选择与n有最大权重节点m;

22. 将m和n构成盒子加入到Box中;

23. 在NodeSet2中删除m和n;

24. End if

25. End

End

定理1 n是一个节点, B是经过两阶段盒子覆盖法产生的盒子, 并且 n∈B, 与节点 n相邻的盒子集合为 M={D1, …, Dm}, 则有 C(n, B-{n})≥C(n, d),其中 d∈B。

证明:

假设 N=(V, E)表示复杂网络, V是网络节点集合, E是网络边集合。设 n是 N中的一个节点(即 n∈V), B1、B2是与 n相邻的两个盒子, 且 n∈B1。假设 n与 B2具有更强的连接, 即 C(n, B1)< C(n, B2)。根据两阶段盒子覆盖法第5行, 在将节点 n放入盒子 B1时, n不包含在更大的完全子图中, 此时 C(n, B1)是与 n相邻盒子中 C值最大的, 即 C(n, B1)> C(n, B2),因此假设不成立。证毕。

定理1表明, 经过两阶段盒子覆盖法节点都被划分到合适的盒子中, 即节点与同一盒子中节点连接是紧密的。

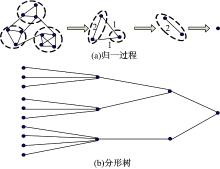
定义3 在复杂网络分形过程中, 每次应用盒子覆盖法时生成的盒子作为父节点, 以盒子包含的节点作为子节点形成一个树形结构, 在下一轮次应用盒子覆盖法时把这个树形结构连接到新生成的树形结构中, 当只有一个节点时分形过程结束, 形成一棵以盒子为节点的树, 称之为分形树。

图2说明了分形树的建立过程。图2(a)为原始网络经过3次应用两阶段盒子覆盖法, 最后归于为一个节点。根据节点与盒子的归属关系可得到此过程的分形树, 如图2(b)所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 分形树建立Fig.2 Create fractal tree

分形树的叶节点是复杂网络原始节点, 所有非叶节点是归一过程中由两阶段盒子覆盖法生成的盒子抽象而来的, 这个盒子是其子节点聚类的结果。由定理1可知每个盒子内的节点有最强的结合能力, 因此在分形树的每一个分支下的节点结合能力是最强的, 而且具有相同父节点的分支结合力强。这与网络社区的特征是相吻合的。研究表明, 很多现实网络演进过程遵循分形树的结构。

FCUC社区检测的方法分为两个阶段完成。第一阶段是创建分形树。这个过程是反复地对网络使用两阶段盒子覆盖法进行归一操作, 直至网络归为一个节点。以归一操作生成的盒子作为父节点, 盒子内包含的节点作为子节点加入到分形树中, 整个分形树是由叶节点向根节点的方向生成。具体生成如算法2所示。第二阶段是对分形树进行分割。鉴于分形树具有分支节点连接紧密的特征, 可以对分形树进行分割, 使分割后的每个分支包含的叶节点构成一个社区。在分割分形树的过程中, 为了得到最优的社区检测结果, 需要对分形树的分割结果进行评估, 选用Newman的 Q函数作为评估函数, 选择 Q函数最大的分割结果作为最终社区检测的结果。 Q函数定义如下:

Q=∑i(eii-ai2)(2)

式中: ai=∑ieij; eij为两个社区间边数量的倒数; Q的范围是 0~1, Q值越大说明社区结构越明显, Q值越小说明网络社区结构不明显。

FCUC社区检测算法框架如算法3所示。

算法2 分形树生成算法

Input

Networks //用邻接矩阵表示的网络

Output

FractalTree //归一操作后生成的分形树

Begin

1. While Networks 节点数> 1

2. Begin

3. boxlist=TSBCA (networks);

//两阶段盒子覆盖法生产盒子列表

4. For i=1 to boxlist.numberOfBox do

5. Begin

6. tree=CreateTree(boxlist[i]);

//根据盒子列表生成每个盒子对应的树形结构

7. FractalTree=FractalTree+tree;

//将盒子对应的树形结构加入分形树中

8. End

9. Networks=renormal(boxlist);

10. End

End

算法3 分形聚类社区检测算法

Input

Networks; //用邻接矩阵表示的网络

Output

CommunityList; //社区检测结果

Begin

Tree=CreateFractalTree(Networks);

//生成分形树

CommunityList =CutTree(Tree);

//以Q函数最大化为目标对分形树进行分割

End

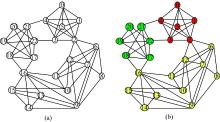
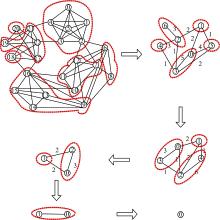
为检验FCUC社区检测算法, 作者在人工网络与现实网络上对其进行了实验。人工网络采用的是Newman提出的人工网络^[9], 其网络结构如图3(a)所示, 该网络有23个节点, 具有明显的社区结构。图3(b)是Newman的快速算法^[5]对该网络检测的社区结构, 结果显示网络包含3个社区。本实验在此人工网络上运行FCUC算法, 图4是应用两阶段盒子覆盖法创建分形树的过程, 从图中可以看出FCUC算法在分形归一过程每次分形操作中盒子与节点的关系。整个归一化过程共进行了5次分形操作, 最终整个网络归一为一个节点。每次分形归一操作由两阶段盒子覆盖法完成, 它将网络中节点聚集到一个盒子中, 进而抽象为一个父节点。在每次归一操作后生成的盒子都具有极强的内部连接。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 人工网络的社区结构Fig.3 Community structure of artificial networks

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 分形归一化过程Fig.4 Renormal progress

图5是对分形树进行分割的过程, 树的叶节点是网络的原始节点, 每个树杈位置是盒子。对于分形树可以有多种分割方案, 本文使用 Q函数对分割方案进行评估, 选择 Q值最大的方案作为检测结果。图中虚线是对分形树进行分割的最佳位置。将分形树分割为3个分支, 每个分支包含的叶节点作为一个社区, 即网络被分为3个社区。可以看到, 检测结果与图3(b)所示的结果一致。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 分形树的分割Fig.5 Cutting fractal tree

FCUC算法对现实世界网络的检测选用了空手道俱乐部网络和海豚网络来进行。

空手道俱乐部网络(Karate)^[18]是美国一所大学空手道俱乐部34名成员间社会关系, 每个节点代表一名成员, 两个节点间有一条边则意味着相应的两个成员之间是交往频繁的朋友关系。用FCUC算法对空手道俱乐部网络的检测结果如图6所示, 网络被分为两个社区。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 空手道社区结构图Fig.6 Community structure of Karate

海豚网络^[19]是Lusseau通过对新西兰神奇湾中62只不同性别海豚观测而构建的动物社会网。网络中每个节点代表一只海豚, 如果两个海豚联系密切, 那么海豚对应的顶点之间就会有一条边连接。这些海豚被天然地分为雄性海豚组和雌性豚组两个社区。图7是FCUC算法对海豚网络的检测结果。FCUC有效地揭示出了海豚网络的社区结构。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 海豚网络社区结构Fig.7 Community structure of dolphin

通过以上对人工网络与现实网络上的测试可以看出, FCUC算法采用两阶段盒子覆盖法能够将连接紧密的节点划分到一个盒子中, 使盒子中节点具有盒子内部节点连接紧密, 盒子与其他盒子连接稀疏的特征。盒子的这种特征使FCUC算法能够从网络演进角度揭示社区结构, 同时FCUC算法也有较强的社区检测能力, 可以有效地检测出复杂网络的社区结构。

本文利用复杂网络的分形特性, 提出了两阶段盒子覆盖法, 并且通过两阶段盒子覆盖法创建分形树。分形树体现了分形聚类的过程, 通过对分形树的分割揭示了复杂网络社区结构。经过在计算机生成网络和现实网络的测试表明, FCUC算法可有效地检测网络社区结构。在后续的研究中, 作者将进一步研究利用分形聚类检测多尺度社区结构, 以及分形聚类与网络演化的关系。