引用本文
马知行, 赵琦, 张浩. 基于傅立叶分析的持家基因预测模型. 2016, 46(5): 1639-1643
MA Zhi-xing, ZHAO Qi, ZHANG Hao. Fourier analysis model for housekeeping gene. Journal of Jilin University Engineering and Technology Edition, 2016, 46(5): 1639-1643  
Permissions
Copyright©2016, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
基于傅立叶分析的持家基因预测模型
马知行1,2, 赵琦3, 张浩3
1.吉林财经大学 管理科学与信息工程学院, 长春 130117
2.吉林财经大学 吉林省互联网金融重点实验室, 长春 130117
3.吉林大学 计算机科学与技术学院, 长春 130012

作者简介:马知行(1983-),男,讲师,博士.研究方向:生物信息.E-mail:mazx716@gmail.com

基金:国家自然科学基金项目(61572225); 国家社会科学基金项目(15BGL090)
摘要

将一组Hela细胞的时序数据通过傅立叶分析变换为傅立叶谱,并设计了基于支持向量机的有监督学习算法,该算法通过提取傅立叶谱中的显著特征鉴定持家基因和非持家基因。本文所提出的方法通过比较两套独立的组织表达谱成功预测了510个人类持家基因,其中包括93个非编码持家基因。分析结果表明:本文方法所预测的持家基因相比其他3种方法更为高效、准确。

关键词: 计算机应用; 持家基因; 支持向量机; 预测模型
中图分类号:TP39 文献标志码:A 文章编号:1671-5497(2016)05-1639-05
Fourier analysis model for housekeeping gene
MA Zhi-xing1,2, ZHAO Qi3, ZHANG Hao3
1.School of Management Science and Information Engineering, Jilin University of Finance and Economics, Changchun 130117, China
2.Jilin Province Key Laboratory of Internet Finance, Jilin University of Finance and Economics, Changchun 130117, China
3.College of Computer Science and Technology, Jilin University, Changchun 130012, China
Abstract

A group of time series data of Hela cells is transformed to Fourier spectrum by Fourier analysis. A support vector machine based monitoring learning algorithm is proposed. This algorithm is applied to pick out the Housekeeping IncRNAs from the Fourier spectrum, which can extract important features of the system, providing a basis for identifying the specific RNAs expression patterns. Using the above method 510 human Housekeeping genes are confirmed, which are then identified by comparison with two standard sets of human tissue specific expression profiles. Results show that the proposed method can give more reliable Housekeeping IncRNAs than three existing identifying methods.

Keyword: computer application; housekeeping gene; support vector machine(SVM); prediction model
0 引 言

持家基因(HKGs)是维持细胞基本功能所需要的组成型基因[1], 它们通常在所有组织类型和细胞阶段稳态表达。上述特性这使HKGs在基因芯片标准化流程中作为可靠的参照物, 使得不同实验条件下产生的生物芯片在质量和数量上具有可比性。随着基于高通量数据的基因组分析手段快速进步, 已经有一批HKGs被预测出来:Warrington[2]和Hsiao[3]分别预测了533条和451条来自于30个不同人体组织的HKG。Eisenberg[4]预测了基于Affymetrix U95A平台包含47个不同组织的575个HKG。经过统计, 上述3个HKG预测集包含总共963个基因, 而它们的交集是150条。这种明显的缺乏一致性预测结果意味着每个集合内都存在高比例的误分类HKG。本文通过前期研究发现, 出现上述问题有两个原因:一是HKGs到现在为止并没有规范化的定义和可进行数学建模的共性生物特征; 二是由于每组芯片表达谱数据实验条件差异巨大, 多数都存在较高的背景噪声。前述研究定义了若干形式化描述HKG的特征, 包括HKG通常具有较短的内含子、非编码区和编码序列, 序列具有这些特征可以使序列的空间结构更紧凑, 便于稳定高效的转录。紧凑的序列结构与持家基因跨组织和发育阶段稳态表达性状是一致的, 因为HKG不需要表达方式具有组织特异性的基因所需的复杂调控。Vinogradov[5]提出HKG的基因间区域相对非持家基因也较短。Zhu[6]比较了HKGs和组织特异性基因的EST数据, 发现HKGs事实上并不具有紧凑基因的结构, 这与前述研究室矛盾的, 进一步为合理定义HKG带来困难。目前为止, 只有HKG的起始非翻译区简单序列重复(SSR)[7]、外显子重复序列[8]以及GC含量[9]三个公认的持家基因统计特征。这些特征作为鉴定HKG和非HKG基因之间的区别是不充分的。经过初步研究发现, 持家基因的自然特征具有一定的表达频谱特征, 这些谱特征可通过基因的时序表达谱数据提取, 并成为鉴定持家基因的依据。本文所提出了基于有限长度离散傅立叶变换[10]的基因时序表达谱数据分析方法, 利用机器学习方法提取了持家基因的谱特征, 预测并验证了510个持家基因。

1 预测模型构建
1.1 数据处理

傅立叶分析对数据的要求是数据持续周期长并且具有较高的采样密度, 但大多数的生化实验所产生的数据都无法满足这个要求, 另外时序数据的长度也无法通过计算方法进行扩展, 如基于血清饥饿的细胞同步方法会在细胞多次分裂后逐渐失去细胞原本的特征, 从而使高斯分布拓宽。如果细胞继续以非同步的方式分裂, 细胞周期特征将完全消失, 出现这种情况即使再长的时间序列也失去了研究的意义。为了满足傅里叶分析对数据的要求, 本文选择一组人的Hela细胞的基因表达时序数据, 这组数据有47个采样点, 每两个相邻采样点间隔时间为1 h, 涵盖3个细胞周期。

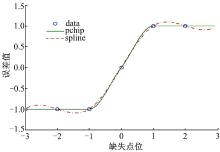
基因表达时间序列上存在一些缺失的数据点是不可避免的, 由于非均匀取样将造成傅里叶分析获得错误结果, 本文对这种缺失采取如下操作:如果缺失数据点连续超过3个, 则将连续缺失点从表达谱中删除; 如果缺失数据是一个单独采样或两个, 本文对其进行分段3次Hermite插值, 此方法不会引起数据整体大规模波动, 是一种比较稳定的插值算法, 该算法的插值数据比其他方法曲线更平滑, 保持数据集固有的周期特征, 详见图1。经过以上操做构建了一个包含32 786均匀采样本的基因表达时序数据集, 数据集覆盖15 261个不同的基因, 规模与人类基因组基本一致。

图1 Hermite插值数据平滑度Fig.1 Hermite interpolation

在通常情况下, 基因表达谱的时序数据并不是静止的, 均值会随时间推移而发生变化。为了使用傅立叶分析揭示基因表达的周期性, 采用基于5个变量的最小二乘法去除时序数据中的干扰分量, 变换时间序列为一阶稳定。参数使用的规则是可以让序列取得最小累计误差, 如图2所示。一套时序数据中的 p个时间点作为向量 X的 p个元素, X=(X(t1), X(t2), …, X(tp))T中, 可以计算向量的 q个基函数, 计算误差如下:

W=∑i=1p[X(ti)-∑j=1qβjEj(ti)]21

图2 去除非周期性数据对集合的影响Fig.2 Effect of removing non-periodic trends from the data

式中: Ej为基函数; βj为基因表述水平均值。

当 ∂W/∂βj=0时, 计算误差最小, 这里使用5个基函数 E1=t, E2=t, E3=t2, E4=ln(5+t), E5=et。

1.2 鉴定持家基因

文献[2, 3, 4]的研究中, 各自都通过分析人体组的表达谱芯片给出了不同的持家基因集合。本文所使用的Hela细胞表达谱包含32 786条有效时序数据系, 其中有234条样本映射158个基因与文献[2, 3, 4]的报道均有交集, 1217个样本所映射的805个基因分别与文献[2, 3, 4]报道中的一个或两个存在交集, 其余31 335个样本映射14 297个基因, 与文献[2, 3, 4]结果不存在交集, 详见图3。在此将以上三类样本分别定义为真实HKGs, 测试HKGs和非HKGs三个集合。

图3 三个HKG集合的探针分布情况Fig.3 Distribution of the probe sets of genes in the three published HKG datasets

为了使基因表达谱的频率分量更为显著, 首先对异阶稳定处理的时序数据进行离散傅立叶变换(Discrete Fourier transform, DFT)。由于每个时序向量都是由47个时间间隔为1 h的采样点组成, 通过式(2)可以获得24个时序频谱特征。

Xk=∑l=0L-1X(tl)e-2πiLkn2

式中: L为时序向量的长度, 取值47; Xk=(k=0, 1, 2, …, L-1)为每个时序数据频率为 k/L的傅立叶谱。

因为表达谱数据47个采样点是实数, 所以频率特征的前23个与后23个共轭, 即 Xk=XL-k* 。因此, 只需要使用24个独立的取值作为SVM训练的特征。

为了测试获得的时间序列的频率组分是否可以区分持家基因与非持家基因, 本文使用有监督统计学习方法。一般来说, 无论一个HKG的表达是否有频率特性, 使用支持向量机(SVM)方法都可以准确鉴定。SVM通过在持家基因和非持家基因的交界处构建一个超平面分类HKGs和非HKGs, SVM建模的目标就是通过特征训练使SVM所构造的这个分界线可以最大程度分类两种类型的基因。这里同时使用24个傅立叶变换后的频率分量作为有效特征, 表示基因之间的区别, 同时用傅立叶变换作为特征中获得的24有效频率分量。高斯径向基函数(RBF)惩罚参数 C=1, 指数参数 γ=0.07。

本文使用两套独立的人体组织的表达谱数据GSE2361和GSE1133作为测试数据, 这两套表达谱是分别为36种和79种正常人体组织的mRNA芯片数据, 可以从GEO自由下载。对两套表达谱数据做log变换, 关联同一个基因的不同实验条件的探针可以在相同水平被我们分析, 来自不同数据集的同一基因标准偏差(SD)和平均值可以被计算, 进一步可以计算改基因的变异系数(CV=SD/均值)。

2 结果分析与讨论

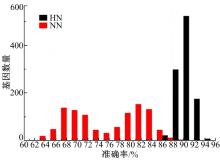
由于HKGs在生命体中各个组织的细胞的全部周期中稳定的表达, 那么HKGs和非HKGs的周期性表达特征应当是有差异, 并且可以观测到。基于这个推断, 本文假设基因表达的频谱特性可用于区分HKGs和非HKGs。本文使用美国斯坦福大学的Hela细胞公开数据集, 其中包含了47 h时序表达的41 508个探针数据, 使用离散傅立叶变换(DFT)对其进行频谱分析, 鉴定基因表达的周期性特征, 并将其形式化地提取出来, 使用SVM机器学习方法鉴定基因是否为HKGs。为了测试一个持家基因表达模式的特征是否可以通过傅立叶谱展现出来, 本文建立了两个基于傅立叶分析所获得的24个频率特征的分类模型:一个是HN模型, 正确区分HKG与非HKG; 另一个是NN模型。两组测试数据均为非持家基因对照组。在HN模型中, 包含234个真实HKG探针作为正样本及234个随机选取的非HKGs作为负样本训练SVM模型。在对照组NN模型中, 随机选取234个非持家基因作为正样本, 在剩余的非持家基因集合中再随机选取234个作为负样本。从图4可以看出, 对照组NN模型区分HKGs和非HKGs的能力显著低于HN模型, 可以证明本文所提出的方法是有效的。

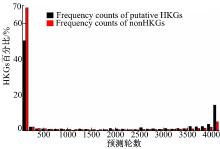
图4 HN、NN模型对比预测能力Fig.4 Ability of the HN and NN models to discriminate

为了避免出现以往预测持家基因集合中较高的假阳性和假阴性数据, 本文只使用234个探针的真实HKGs作为SVM训练的正样本, 这234个真实持家基因是以往工作所共同发现的, 再从31 335个非持家基因探针中随机选取234个探针作为负样本。在预测模型进行一轮预测后, 一些非持家基因会被分类为持家基因, 即存在随机偏差, 这种偏差可以消除, 也就是在多轮预测后将那些多次被判定为持家基因的数据列为正样本。通过计算机仿真对本文方法是否对不同时间序列数据具有鲁棒性进行测试, 仿真结果表明, 本文方法是鲁棒的, 可以识别不同的频率模式。图5为4096(212)轮随机预测中发现真实持家基因的概率分布。从图中可以看出, 随机预测次数足够多的前提下, 负样本集合中的误判真持家基因全部可以被正确识别。有299个持家基因从805待定HKG中被重新归类, 用计数次数3328作为重判定的分界点。另外, 还有53个非持家基因被本文方法从原有分类中重新划分, 因为它们各自至少在4085轮预测中被鉴定为持家基因。采用本文所提出的鉴定方法共发现持家基510个。

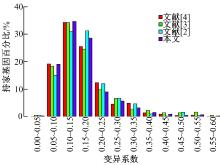
图5 持家基因计数分布Fig.5 HKG count distribution

本文使用了两套独立的表达谱数据作为测试数据以评估本文方法的有效性, 这两套数据分别来自于115个不同的人体组织细胞。一个基因是否为持家基因, 可以通过度量该基因的变异系数判定, 低水平的变异系数表明该基因在所有组织中高表达。图6和图7显示了本文方法与文献[2, 3, 4]中方法所获得的15 261个持家基因的变异系数分布差异, 结果表明, 本文方法所预测的持家基因变异系数明显小于其他3种方法所预测的持家基因集合。

图6 数据集GSE2361变异系数比较Fig.6 GSE2361 distribution of CVs

图7 数据集GSE1133变异系数比较Fig.7 GSE1133 distribution of CVs

对本文方法所预测的持家基因进行了基因本体分析, 它们的功能分类如图8所示。结果表明, 预测的HKG主要分布在细胞凋亡周期、代谢过程和生物调控这几个重要的生物学过程中, 也侧面证明了本文预测方法的有效性。

图8 持家基因本体论分布Fig.8 Distribution of gene ontology in our predicted HKG set

本文对预测集合中基因序列的保守性做了分析, 图8显示了在不同的基因组中文献[2, 3, 4]方法与本文方法的比较, 结果表明, 预测序列的保守趋势是一致的, 持家基因由于其本身特性较少出现序列变化, 本文的预测结果与这一事实具有一致性, 证明了本文方法的有效性。

3 结束语

通过对基于傅立叶分析的持家基因预测方法的研究, 建立了从时序基因表达谱数据鉴定持家基因的模型。该模型为基因功能研究提供了有效工具, 并且也为其他研究者在公开数据集中从事相关研究提供了借鉴。

The authors have declared that no competing interests exist.

参考文献
[1] Bolstad B M, Irizarry R A, Astrand M, et al. A comparison of normalization methods for high density oligonucleotide array data based on variance and bias[J]. Bioinformatics, 2003, 19(2): 185-193. [本文引用:1]
[2] Huttenrauch F, Nitzki A, Lin F T, et al. Comparison of human adult and fetal expression and identification of 535 housekeeping/maintenance genes[J]. Physiological Genomics, 2000, 2(3): 143-147. [本文引用:7]
[3] Hsiao L L, Dangond F, Yoshida T, et al. A compendium of gene expression in normal human tissues[J]. Physiological Genomics, 2001, 7(2): 97-104. [本文引用:7]
[4] Eisenberg E, Levanon E Y. Human housekeeping genes are compact[J]. Trends in Genetics, 2003, 19(7): 362-365. [本文引用:7]
[5] Vinogradov A E. Compactness of human housekeeping genes: selection for economy or genomic design?[J]. Trends in Genetics, 2004, 20(20): 248-253. [本文引用:1]
[6] Jiang Z, He F, Hu S, et al. On the nature of human housekeeping genes[J]. Trends in Genetics, 2008, 24(10): 481-484. [本文引用:1]
[7] Lawson M J, Zhang L. Housekeeping and tissue-specific genes differ in simple sequence repeats in the 5'-UTR region[J]. Gene, 2008, 407(1/2): 54-62. [本文引用:1]
[8] Eller C D, Regelson M, Merriman B, et al. Repetitive sequence environment distinguishes housekeeping genes[J]. Gene, 2007, 390(1/2): 153-165. [本文引用:1]
[9] Vinogradov A E. Isochores and tissue-specificity[J]. Nucleic Acids Research, 2003, 31(17): 5212-5220. [本文引用:1]
[10] 余军, 张长海, 张浩, 等. 基于茎区的动态规划算法的核糖核酸二级结构预测[J]. 吉林大学学报: 工学版, 2011, 41(2): 452-457.
Yu Jun, Zhang Chang-hai, Zhang Hao, et al. Prediction of RNA secondary structure using dynamic programming algorithm based on stems[J]. Journal of Jilin University(Engineering and Technology Edition), 2011, 41(2): 452-457. [本文引用:1]