基于混沌搜索的蜂窝网基站能量效率与服务质量的联合优化

引用本文

刘宁庆, 韩雪, 张文彬. 基于混沌搜索的蜂窝网基站能量效率与服务质量的联合优化. 2016, 46(5): 1660-1666
LIU Ning-qing, HAN Xue, ZHANG Wen-bin. Joint optimization of energy efficiency and QoS of cellular base station based on caotic search. Journal of Jilin University Engineering and Technology Edition, 2016, 46(5): 1660-1666 复制到剪切板

Permissions

基于混沌搜索的蜂窝网基站能量效率与服务质量的联合优化

刘宁庆¹, 韩雪^1,², 张文彬¹

1.哈尔滨工业大学电子与信息工程学院, 哈尔滨 150001

2.哈尔滨电工仪表研究所国际标准工作站, 哈尔滨 150028

作者简介:刘宁庆(1959-),男,研究员.研究方向:数据通信.E-mail:nqliu@hit.edu.cn

基金:国家自然科学基金项目(61301100).

摘要

针对蜂窝网络中基站能量效率和用户服务质量的联合优化问题,结合实际的蜂窝网络中基站与用户终端选择连接的原则,建立了反映基站能量效率和用户终端服务质量的数学模型。采用基于幂函数载波技术的混沌搜索算法对优化问题进行求解,并证明了算法的收敛性。仿真结果验证了模型的有效性及设计算法的可行性。

关键词: 通信技术; 蜂窝网络优化模型; 混沌搜索算法; 能量效率

中图分类号:TN929 文献标志码:A 文章编号:1671-5497(2016)05-1660-07

Joint optimization of energy efficiency and QoS of cellular base station based on caotic search

LIU Ning-qing¹, HAN Xue^1,², ZHANG Wen-bin¹

1.School of Electronics and Information Engineering, Harbin Institute of Technology, Harbin 150001,China

2.International Standard Workstation,Harbin Research Institute of Electrical Instruments,Harbin 150028,China

Abstract

To solve the joint optimization problem of energy efficiency and customer service quality of the base station in a cellular network, considering the actual connection principle between base station and the user terminal of cellular network, a mathematical model is established that reflects the base station energy efficiency and user terminal service. The chaotic search algorithm based on power function carrier technology is applied to solve the optimization problem. The convergence of the algorithm is proved. Simulation results validate the model and the feasibility of the algorithm.

Keyword: communication technology; cellular network optimization model; chaotic search algorithm; energy efficiency

Show Figures

0 引言

无线移动通信的“ 绿色化” 已成为目前通信领域重要的研究方向, 是亟待研究发展的重大前沿课题^[1]。在蜂窝网络中, 根据流量负载的变化来进行小区伸缩是节约能量的有效策略。在此策略中, 如何确定哪些基站进入休眠模式、哪些基站扩大覆盖范围是一个关键问题^{[2, 3, 4, 5]}。文献[2]证明了通过基站切换进行节能的可行性; 文献[3]针对基站不同的关掉比例, 采用简化分析方法研究基站切换策略并应用于蜂窝网络, 另外, 这种方法也考虑了切换前和切换后移动台所归属的两个不同的效用平衡^[4]。在这些问题的背景下, 本文研究了基于基站能量效率和移动终端服务质量的通信选择策略, 构建了联合优化二者的数学模型, 并采用混沌搜索算法寻找该模型的近似最优解。

1 系统模型

本文采用能量效率的通用定义^[6], 即:能量效率等于每单位能量传输的数据比特数, 考虑到电路损耗, 能量效率 $\begin{matrix} η_{EE} \end{matrix}$ 表示为:

$\begin{matrix} η_{EE} = \frac{R}{(P_{T} + P_{c})} (1) \end{matrix}$

式中: $R$ 为数据传输速率; $\begin{matrix} P_{c} \end{matrix}$ 为电路损耗功率, 主要包含传输数据的过程中的信号处理能耗、数字模拟转换器件能耗和射频前端模拟器件能耗等, 它与传输速率无关, 通常为固定值; $\begin{matrix} P_{T} \end{matrix}$ 为发射功率, 模型设定蜂窝小区采用时分双工制式(TDD), 每个用户占用一个时隙, 基站为每个用户预留了固定的功率值, 基站在每个时隙发送的功率为固定值 $\begin{matrix} p_{j} 。 \end{matrix}$

本文选定多小区下行蜂窝网络作为系统场景, 设定该网络中有 $\begin{matrix} M \end{matrix}$ 个基站和 $\begin{matrix} N \end{matrix}$ 个移动终端。第 $\begin{matrix} m \end{matrix}$ 个基站和第 $\begin{matrix} n \end{matrix}$ 个移动终端分别用 $\begin{matrix} b_{m} \end{matrix}$ 和 $\begin{matrix} u_{n} \end{matrix}$ 来表示, 它们之间的路径损耗用 $\begin{matrix} p l_{m, n} \end{matrix}$ 来表示。假设系统带宽为 $\begin{matrix} B, {p_{m}}^{b} \end{matrix}$ 表示基站 $\begin{matrix} b_{m} \end{matrix}$ 的发射功率, 基站为每个覆盖区域内的用户分配相同的功率, $\begin{matrix} σ^{2} \end{matrix}$ 表示噪声功率。对于与基站 $\begin{matrix} b_{m} \end{matrix}$ 连接的移动终端 $\begin{matrix} u_{n} \end{matrix}$ 来说, 它的信号干扰噪声功率比(SINR)为:

$\begin{matrix} γ_{m, n} = \frac{p l_{m, n} {p_{m}}^{b}}{\overset{M}{\sum_{k = 1, k \neq m}} p l_{k, n} {p_{k}}^{b} + σ^{2}} (2) \end{matrix}$

基站 $\begin{matrix} b_{m} \end{matrix}$ 到移动终端 $\begin{matrix} u_{n} \end{matrix}$ 之间的数据速率为:

$\begin{matrix} R_{m, n} = B_{m, n} lo g_{2} (1 + γ_{m, n}) (3) \end{matrix}$

式中: $\begin{matrix} B_{m, n} \end{matrix}$ 为基站 $\begin{matrix} b_{m} \end{matrix}$ 分配给移动终端 $\begin{matrix} u_{n} \end{matrix}$ 的带宽。

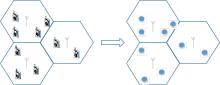
蜂窝网络中的基站与移动终端之间的连接关系可以用加权二部图来表示, 按照二部图的方法可以将蜂窝网络演变成如图1所示的模型^{[7, 8]}。

	Figure Option View Download New Window
	图1 蜂窝网络演变模型Fig.1 Cellular network evolution model

定义连接矩阵 $\begin{matrix} X = {(x_{m, n})}_{M \times N}, \end{matrix}$ 用该矩阵表示蜂窝网络中基站与移动终端之间的连接关系:

$\begin{matrix} x_{m, n} = \{\begin{matrix} 1, b_{m} 与 u_{n} 连接 \\ 0, b_{m} 与 u_{n} 未连接 \end{matrix} \end{matrix}$

蜂窝系统的服务质量(QoS)用移动终端(u_n)的SINR值表示, 蜂窝系统的能量效率用基站的能量效率公式表示。由于高SINR值与高能量效率是系统追求的两个方面, 但二者又相互制约, 所以这里用权值矩阵 $\begin{matrix} W = {(w_{m, n})}_{M \times N} \end{matrix}$ 为这两个方面做一个折中, 即定义基站 $\begin{matrix} b_{m} \end{matrix}$ 与移动终端 $\begin{matrix} u_{n} \end{matrix}$ 之间的权值为:

$\begin{matrix} \begin{matrix} w_{m, n} = α {\overset{\land}{γ}}_{m, n} + β {\overset{\land}{η}}_{m} = \\ α \frac{γ_{m, n}}{\max_{i} γ_{i, n}} + β \frac{\frac{\sum_{j} R_{m, j} x_{m, j}}{{p_{m}}^{b} + P_{c}}}{\max_{k} \frac{\sum_{l} R_{k, l} x_{k, l}}{{p_{k}}^{b} + P_{c}}} (4) \end{matrix} \end{matrix}$

式中: $\begin{matrix} {\overset{\land}{γ}}_{m, n} \end{matrix}$ 和 $\begin{matrix} {\overset{\land}{η}}_{m} \end{matrix}$ 分别为移动终端 $\begin{matrix} u_{n} \end{matrix}$ 的归一化SINR值和基站 $\begin{matrix} b_{m} \end{matrix}$ 的归一化能量效率值; 令 $\begin{matrix} α + β = 1, α \end{matrix}$ 为服务质量(QoS)因子, $\begin{matrix} β \end{matrix}$ 为基站能量效率因子, 可以通过调节 $\begin{matrix} α \end{matrix}$ 和 $\begin{matrix} β \end{matrix}$ 的值来改变用户在重新选择连接基站过程中要考虑因素的比重, 若在此过程中重点考虑系统的服务质量, 则相应加大 $\begin{matrix} α \end{matrix}$ 的值, 反之, 则加大 $\begin{matrix} β \end{matrix}$ 的值。

经过上述的推导过程, 蜂窝系统已经建模成一个加权二部图, 这里定义加权二部图的总权值 $\begin{matrix} V \end{matrix}$ 来表示蜂窝系统的整体性能:

$\begin{matrix} V = \overset{M}{\sum_{m = 1}} \overset{N}{\sum_{n = 1}} w_{m, n} x_{m, n} (5) \end{matrix}$

把权衡蜂窝系统的服务质量(QoS)与基站的能量效率两方面因素看作一个优化问题, 相应的目标函数为:

$\begin{matrix} \begin{matrix} \max & V \end{matrix} (6) \end{matrix}$

根据式(4)(5)(6)推导出目标函数为:

$\begin{matrix} \begin{matrix} \max \overset{M}{\sum_{m = 1}} \overset{N}{\sum_{n = 1}} w_{m, n} x_{m, n} = \\ \max \overset{M}{\sum_{m = 1}} \overset{N}{\sum_{n = 1}} (α \frac{γ_{m, n}}{\max_{i} γ_{i, n}} + β \frac{\frac{\sum_{j} R_{m, j} x_{m, j}}{{p_{m}}^{b} + P_{c}}}{\max_{k} \frac{\sum_{l} R_{k, l} x_{k, l}}{{p_{k}}^{b} + P_{c}}}) x_{m, n} (7) \end{matrix} \end{matrix}$

约束条件如下:

$\begin{matrix} \{\begin{matrix} x_{m, n} = 1 or 0 \\ \overset{M}{\sum_{m = 1}} x_{m, n} = 1, \forall n \\ \overset{N}{\sum_{n = 1}} x_{m, n} \leq j, 1 \leq j \leq N, \forall m \end{matrix} (8) \end{matrix}$

通过推导出的目标函数, 将最优化问题转化为只与连接矩阵 $\begin{matrix} X \end{matrix}$ 有关的0-1规划问题。目前求解0-1整数规划问题的常用方法有分枝定界法、完全枚举法、动态规划法和遗传算法等。当问题规模较大时, 使用前3种方法计算量将非常大, 求解困难, 甚至无法求解。而遗传算法虽具有全局寻优能力, 但容易陷入局部最优解。因此, 本文设计了改进的混沌搜索算法来求解式(7)的优化问题。

2 改进的混沌搜索算法

混沌是非线性系统中较为普遍的一种现象, 相应的混沌搜索算法被广泛应用于非线性优化领域^[9]。本文首先通过罚函数法吸收掉式(8)中第三个约束条件, 然后利用基于幂函数载波技术的混沌搜索算法来兼容式(8)中第一、第二个约束条件。

(1)利用罚函数吸收约束条件

根据式(8)中的约束条件:

$\begin{matrix} \overset{N}{\sum_{n = 1}} x_{m, n} \leq j, 1 \leq j \leq N, \forall m \end{matrix}$

将原目标函数转化为如下无约束优化问题:

$\begin{matrix} maxV = \max \{f (X) - σmax (\overset{N}{\sum_{n = 1}} x_{m, n} - j, 0)\} (9) \end{matrix}$

式中: $\begin{matrix} σ \end{matrix}$ 为任意给定的足够大的一个正数; $\begin{matrix} \begin{matrix} X = [x_{1, 1}, \dots, x_{1, N}, x_{2, 1}, \dots, x_{2, N}, \dots, x_{M, 1}, \dots, x_{M, N}]; f (x_{1, 1}, \dots, x_{1, N}, x_{2, 1}, \dots, x_{2, N}, \dots, x_{M, 1}, \dots, x_{M, N}) \\ = \overset{M}{\sum_{m = 1}} \overset{N}{\sum_{n = 1}} (α \frac{γ_{m, n}}{\max_{i} γ_{i, n}} + β \frac{\frac{\sum_{j} R_{m, j} x_{m, j}}{{p_{m}}^{b} + P_{c}}}{\max_{k} \frac{\sum_{l} R_{k, l} x_{k, l}}{{p_{k}}^{b} + P_{c}}}) x_{m, n} \end{matrix} \end{matrix}$ 。

(2)基于幂函数载波技术的混沌搜索算法

本文采用基于幂函数载波技术的混沌搜索算法^[10]求解式(9)中的目标函数, 具体步骤如下:

①利用混沌变量对初值的敏感性, 随机产生 $\begin{matrix} N \end{matrix}$ 个[0, 1]之间的不同混沌变量初值 $z_{i, k}, i = 1, \dots, N; k = 0$ 。设定终止循环次数为 $L$ , 同时初始化迭代计数变量 $\begin{matrix} l = 0, V^{*} = V (x_{m, n} (0)), x_{m, n}^{*} = x_{m, n} (0) 。 \end{matrix}$ 其中, 初值不能取0、0.25、0.5、0.75和1这几个点。

②根据幂函数载波技术的公式:

$\begin{matrix} z_{i, k'} = \{\begin{matrix} z_{i, k}^{u}, \\ z_{i, k}, \\ z_{i, k}^{v}, \end{matrix} \begin{matrix} z_{i, k} \in (0, a], 0 < u < 1 \\ z_{i, k} \in (a, b] \\ z_{i, k} \in (b, 1], v > 1 \end{matrix} (10) \end{matrix}$

设定 $\begin{matrix} u = 0.46, v = 13.6, a = 0.15, b = 0.96 。 \end{matrix}$

③将[0, 1]区间划分成 $M$ 个相等的小区间, 即 $[0, 1 / M), [1 / M, 2 / M), \dots, [(M - 1) / M, 1)$ , 并将生成地区间依次编号为 $\begin{matrix} 1 ~M 。 \end{matrix}$

④判断迭代生成的 $N$ 个混沌变量 $\begin{matrix} z_{i, k'} (i = 1, 2, \dots, N) \end{matrix}$ 所在的区间范围, 并相应地设置如下:

$\begin{matrix} x_{m, n} (k) = \{\begin{matrix} 1, 第 n 个混沌变量落在 \\ 第 m 个区间上 \\ 0, 第 n 个混沌变量不落在 \\ 第 m 个区间上 \end{matrix} \end{matrix}$

前4个步骤已经把除了罚函数中用到的约束条件以外的两个约束条件实现了, 不需要再将其转化为惩罚项。

⑤分别用产生的混沌变量计算目标函数 $\begin{matrix} V (x_{m, n} (k)) \end{matrix}$ 并进行比较, 若 $\begin{matrix} V (x_{m, n} (k)) > V^{*}, \end{matrix}$ 则令 $\begin{matrix} V^{*} = V (x_{m, n} (k)), x_{m, n}^{*} = x_{m, n} (k), \end{matrix}$ 置 $\begin{matrix} l = 0, \end{matrix}$ 利用公式 $k = k + 1, z_{i, k} = μ z_{i, k'} (1 - z_{i, k'})$ 生成 $\begin{matrix} N \end{matrix}$ 个新的混沌变量, 然后跳转到步骤②; 反之, 放弃 $x_{m, n} (k)$ , 并令 $\begin{matrix} l = l + 1 。 \end{matrix}$

⑥如果 $\begin{matrix} l \end{matrix}$ 满足终止条件(根据搜索数据量的大小适当选择一个合适搜索次数作为终止条件), 则停止搜索, 输出最优解 $\begin{matrix} V^{*}, x_{m, n}^{*}; \end{matrix}$ 反之, 利用公式 $k = k + 1, z_{i, k} = μ z_{i, k'} (1 - z_{i, k'})$ 生成 $\begin{matrix} N \end{matrix}$ 个新的混沌变量, 然后跳转到步骤②, 继续求解。

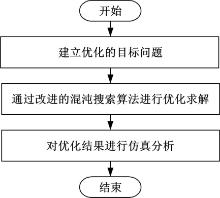
本文优化问题从建模到求解的整个过程如图2所示。

	Figure Option View Download New Window
	图2 问题优化流程图Fig.2 Flow chart of problem optimization

(3)混沌搜索算法收敛性的证明

设 $\begin{matrix} x^{k} \end{matrix}$ 是由混沌搜索算法求解出来的解, 目标函数设为 $\begin{matrix} f (x), x^{*} \end{matrix}$ 为目标函数的最优解, 则证明 $\begin{matrix} f (x^{k}) \end{matrix}$ 以概率1收敛到全局最优解 $\begin{matrix} f (x^{*}), \end{matrix}$ 可以说明混沌搜索算法具有收敛性。

证明过程如下:

设 $\begin{matrix} Rx = \{x\} x \in s, f (k) - f (x^{*}) < δ\}, \end{matrix}$ 当 $\begin{matrix} δ \end{matrix}$ 充分小时, $\begin{matrix} Rx \end{matrix}$ 表示全局最优点 $\begin{matrix} x^{*} \end{matrix}$ 的 $\begin{matrix} δ \end{matrix}$ 邻域。混沌搜索算法产生的序列 $\begin{matrix} x^{k} \end{matrix}$ 落入 $\begin{matrix} Rx \end{matrix}$ 内的事件集合记为 $\begin{matrix} A_{k} = \{k | x^{k} \in Rx\} 。 \end{matrix}$ 这里以求解限定条件内的最小值为例, 故混沌搜索算法为下降算法。每次该算法产生的搜索序列 $\begin{matrix} x^{1}, x^{2}, \dots, x^{k}, \dots, x^{\infty} \end{matrix}$ 都是一个随机过程的样本函数的离散值, 这些随机变量本身可取样本空间中任意值, 但要满足:

$\begin{matrix} f (x^{1}) - f (x^{*}) \geq \dots \geq f (x^{k}) - f (x^{*}) \geq \dots \end{matrix}$

根据上述条件, 假设第3个元素 $\begin{matrix} x^{3} \end{matrix}$ 落在全局最优点 $\begin{matrix} x^{*} \end{matrix}$ 的 $\begin{matrix} δ \end{matrix}$ 邻域, 则 $\begin{matrix} x^{4}, x^{5}, \dots, x^{\infty} \end{matrix}$ 也一定落在全局最优点 $\begin{matrix} x^{*} \end{matrix}$ 的 $\begin{matrix} δ \end{matrix}$ 邻域, 记为 $\begin{matrix} A_{3}; \end{matrix}$ 同理假设第4个元素 $\begin{matrix} x^{4} \end{matrix}$ 落在全局最优点 $\begin{matrix} x^{*} \end{matrix}$ 的 $\begin{matrix} δ \end{matrix}$ 邻域, 记为 $\begin{matrix} A_{4}; \end{matrix}$ 以此类推, 这样的样本函数集合满足:

$\begin{matrix} A_{1} \supset A_{2} \supset \dots \supset A_{k} \supset \dots \end{matrix}$

当 $\begin{matrix} k \to \infty \end{matrix}$ 时, 事件集合 $\begin{matrix} A_{k} = \{k | x^{k} \in Rx\} \end{matrix}$ 的概率 $\begin{matrix} p (A_{k}) \end{matrix}$ 等于 $\begin{matrix} p (A_{\infty}), \end{matrix}$ 等价于 $\begin{matrix} \{\infty| x^{\infty} \in Rx\}, \end{matrix}$ 也可以理解为 $\begin{matrix} A_{1}, A_{2}, \dots, A_{\infty} \end{matrix}$ 中只要有一个事件集合发生, $\begin{matrix} A_{\infty} \end{matrix}$ 就一定发生。所以, $\begin{matrix} \lim_{k \to \infty} p (A_{k}) = p (\overset{\infty}{⋃_{k = 1}} A_{k}), \end{matrix}$ 根据单调有界数列必收敛可得:

$\begin{matrix} \lim_{k \to \infty} p (A_{k}) = p (\overset{\infty}{⋃_{k = 1}} A_{k}) = 1 (11) \end{matrix}$

取一个(0, 1)之间的正数 $\begin{matrix} V, \end{matrix}$ 根据高等数学中关于极限的定义可知, 一定存在一个正数 $\begin{matrix} M, \end{matrix}$ 使得当 $\begin{matrix} k > M \end{matrix}$ 时, $\begin{matrix} 1 - p (A_{k}) \leq V 。 V \end{matrix}$ 越小, 说明对应的 $\begin{matrix} M \end{matrix}$ 越大。由此可得:

$\begin{matrix} \begin{matrix} 1 - p (A_{k}) = p \{k | k \notin A_{k}, k > M\} = \\ 1 - p \{k | k \in A_{k}, k > M\} (12) \end{matrix} \end{matrix}$

式中: $\begin{matrix} p \{k | k \notin A_{k}, k > M\} \end{matrix}$ 表示第 $\begin{matrix} k \end{matrix}$ 个随机变量不位于全局最优点 $\begin{matrix} x^{*} \end{matrix}$ 的 $\begin{matrix} δ \end{matrix}$ 邻域内; $\begin{matrix} p \{k | k \in A_{k}, k > M\} \end{matrix}$ 表示第 $\begin{matrix} k \end{matrix}$ 个随机变量位于全局最优点 $\begin{matrix} x^{*} \end{matrix}$ 的 $\begin{matrix} δ \end{matrix}$ 邻域内, 很显然, 二者和为1。

现取一个大于 $\begin{matrix} M \end{matrix}$ 的数值 $\begin{matrix} Q \end{matrix}$ , 可知:

$\begin{matrix} \begin{matrix} p \{Q | f (x^{Q}) - f (x^{*}) > δ\} = \\ p \{Q | Q \notin A_{Q}\} = \\ p \{Q | Q \notin A_{Q}, Q > M\} (13) \end{matrix} \end{matrix}$

在 $\begin{matrix} Q \end{matrix}$ 之前的数列元素的函数值一定不在全局最优点的邻域内, 即 $\begin{matrix} p {1 | 1 \notin A_{1}}, p {2 | 1 \notin A_{2}}, \dots, p {M | 1 \notin A_{M}} \dots, p \{(Q - 1) | 1 \notin A_{(Q - 1)}} \end{matrix}$ 不在最优点邻域内。所以式(13)的概率值为上述各事件的概率乘积, 可得:

$\begin{matrix} \begin{matrix} p \{Q | f (x^{Q}) - f (x^{*}) > δ\} = \\ p \{Q | Q \notin A_{Q}\} \leq V \cdot V \cdot V \dots \leq V^{Q - M - 1} (14) \end{matrix} \end{matrix}$

当 $\begin{matrix} Q \to \infty \end{matrix}$ 时, 有:

$\begin{matrix} \begin{matrix} 0 \leq \lim_{Q \to \infty} p \{Qf (x^{Q}) - f (x^{*}) > δ\} \leq \\ \lim_{Q \to \infty} V^{Q - M - 1} = 0 \end{matrix} \end{matrix}$

将式中的 $\begin{matrix} Q \end{matrix}$ 换为 $\begin{matrix} k \end{matrix}$ 可得:随着 $\begin{matrix} k \end{matrix}$ 的增大, $\begin{matrix} x^{k} \end{matrix}$ 落入全局最优点 $\begin{matrix} x^{*} \end{matrix}$ 的 $\begin{matrix} δ \end{matrix}$ 邻域外的概率为0, 这表明 $\begin{matrix} f (x^{k}) \end{matrix}$ 以概率1收敛到全局最优解 $\begin{matrix} f (x^{*}) 。 \end{matrix}$

3 仿真验证

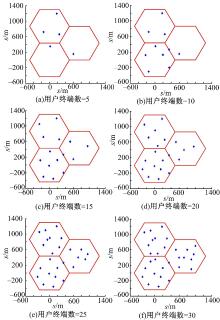
系统仿真场景为3小区蜂窝网络, 如图3所示, 用户随机地分布在小区中, 用户数从5到30递增。设定蜂窝小区采用时分双工制式(TDD), 每个用户占用一个时隙, 基站在每个时隙发送的功率为固定值 $\begin{matrix} p_{j}, \end{matrix}$ 则当某基站与 $\begin{matrix} n \end{matrix}$ 个用户终端连接时所需的发射功率为 $\begin{matrix} n \cdot p_{j} 。 \end{matrix}$ 在GSM蜂窝系统中, 基站发射功率为每载波500 W, 每个载波含有8个时隙, 8个时隙构成一个TDMA帧, 则每个时隙发射功率为500 W/8=62.5 W。

	Figure Option View Download New Window
	图3 蜂窝网络分布Fig.3 Distribution of cellular network

仿真过程中的参数如下:小区半径为500 m; 载波频率为2 GHz; 载波间隔为10 MHz; 噪声功率为-174 dB· W/Hz; 小区数为3; 用户数为5~30; 每个时隙的发送功率为62.5 W; 电路损耗(占整个功耗的4%左右)为200 W。

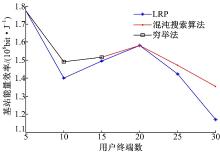
目前实际的蜂窝网络中用户与基站的连接准则是:用户与能为自己提供最大接收功率的基站相连接, 称之为LRP(Largest receive power)准则。在仿真过程中将本文设计的混沌搜索算法求解出的近似最优解与用穷举法求出的最优解以及LRP方式作比较。

根据图4可以看出, 通过穷举法与混沌搜索算法对优化问题进行求解得到的基站与用户连接选择, 其能量效率值高于或等于LRP连接情况下的值; 随着蜂窝网络内用户终端数量的增加, 无论是LRP模式下还是通过求解优化问题得到的连接情况, 基站的能量效率整体趋势是在逐渐降低。在5~15个用户之间, 混沌搜索算法可以通过有限的搜索步数找到穷举法得到的解, 故在仿真图中出现两条曲线重合的情况; 在20~30个用户之间, 由于连接矩阵 $\begin{matrix} X \end{matrix}$ 的可能种数达到了3²⁰~3³⁰, 已经无法用穷举法进行验证, 只有混沌搜索算法寻找到的近似最优解。

	Figure Option View Download New Window
	图4 能量效率与用户终端数Fig.4 Number of users and energy efficiency

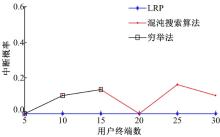
通过图5可以看出, 两种模式下的用户终端的中断概率不相同, 在LRP模式下, 用户总是与能够为自己提供最大接收功率的基站连接, 所以中断概率为0; 而通过最大化目标函数求解的状态下, 出现少量的中断情况, 这是为了提高能量效率付出的代价。

	Figure Option View Download New Window
	图5 中断概率与用户终端数Fig.5 Blocking probability and the number of users

能量效率定义为每单位能量下传输的数据比特数, 而这里的能量不仅包括发射功率, 还包括电路损耗功率。用户终端数较少时, 用户连接基站分布较集中, 这样既能有较高的能量效率, 也能很好地保证用户的QoS, 但随着用户数的增加, 受限于QoS的制约, 在一定的概率下, 用户终端不会再集中连接在某一个基站上, 从而导致能量效率的降低。

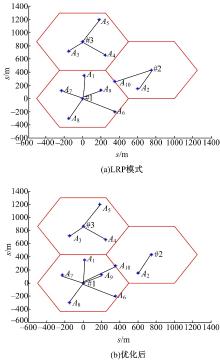
仿真过程中取3基站、10用户为例, LRP模式下的连接情况以及优化后的连接情况如图6所示, 基站与用户之间对应的距离如表1所示。

	Figure Option View Download New Window
	图6 连接情况Fig.6 Connection mode

表1 基站与用户之间的距离 Table 1 Distance between the base station and users m

下面通过数学推导来证明本文优化模型下的能量效率优于LRP模式下的能量效率。

假定两个蜂窝小区各有两个移动终端, 分别为 $\begin{matrix} A_{1} 、 A_{2} 、 A_{3} 、 A_{4}, \end{matrix}$ 分布如图7所示。

	Figure Option View Download New Window
	图7 两小区分布Fig.7 Distribution of two residential

根据LRP准则, 它们分别与最近的基站连接, 对应传输速率分别为 $\begin{matrix} R_{1} 、 R_{2} 、 R_{3} 、 R_{4}, \end{matrix}$ 每个时隙的发送功率为 $\begin{matrix} P_{T}, \end{matrix}$ 电路损耗功率为 $\begin{matrix} P_{c}, \end{matrix}$ 则LRP模式下的能量效率值为:

$\begin{matrix} η_{LRP} = \frac{R_{1} + R_{2}}{2 P_{T} + P_{c}} + \frac{R_{3} + R_{4}}{2 P_{T} + P_{c}} (15) \end{matrix}$

当用户 $\begin{matrix} A_{3} \end{matrix}$ 选择与基站1连接的情况下, 能量效率值为:

$\begin{matrix} η = \frac{R_{1} + R_{2} + R'_{3}}{3 P_{T} + P_{c}} + \frac{R_{4}}{P_{T} + P_{c}} (16) \end{matrix}$

其中, 由于用户 $\begin{matrix} A_{3} \end{matrix}$ 与基站1的距离比基站2远, 路径损耗更多, 数据传输损率相对要低, 即 $\begin{matrix} R'_{3} < R_{3} 。 \end{matrix}$ 将式(15)(16)作比较有:

$\begin{matrix} \begin{matrix} \frac{R_{1} + R_{2}}{2 P_{T} + P_{c}} + \frac{R_{3} + R_{4}}{2 P_{T} + P_{c}} - \\ (\frac{R_{1} + R_{2} + R'_{3}}{3 P_{T} + P_{c}} + \frac{R_{4}}{P_{T} + P_{c}}) = \\ \frac{A - B}{(2 P_{T} + P_{c}) (3 P_{T} + P_{c}) (P_{T} + P_{c})} (17) \end{matrix} \end{matrix}$

式中:

$\begin{matrix} \begin{matrix} A = (P_{T} + P_{c}) [(R_{1} + R_{2}) P_{T} + R_{3} (3 P_{T} + P_{c}) - \\ R'_{3} (2 P_{T} + P_{c})]; \\ B = R_{4} (3 P_{T} + P_{c}) P_{T}; \end{matrix} \end{matrix}$

分子可以化简如下:

$\begin{matrix} \begin{matrix} A - B = (R_{1} + R_{2}) (P_{T} + P_{c}) P_{T} + \\ (P_{T} + P_{c}) [R_{3} (3 P_{T} + P_{c}) - \\ R'_{3} (2 P_{T} + P_{c})] - R_{4} (3 P_{T} + P_{c}) P_{T} < \\ (R_{1} + R_{2} + R_{3}) (P_{T} + P_{c}) P_{T} - \\ R_{4} (3 P_{T} + P_{c}) P_{T} (18) \end{matrix} \end{matrix}$

对于式(18), 传输速率 $\begin{matrix} R_{1} 、 R_{2} 、 R_{3} 、 R_{4} \end{matrix}$ 之间的大小关系是由基站与用户间的距离决定的, 当距离特别近导致 $\begin{matrix} R_{4} \end{matrix}$ 很大时, 由于 $\begin{matrix} 3 P_{T} + P_{c} > P_{T} + P_{c}, \end{matrix}$ 导致最终式子小于0; 反之, 当 $\begin{matrix} R_{1} + R_{2} + R_{3} > R_{4}, \end{matrix}$ 式子又可能最终大于0。即两种情况下的能量效率值不是固定不变的关系, 这也是进行优化的目的所在。

混沌搜索算法与穷举法的复杂度对比如表2所示。

表2 混沌算法和穷举法的复杂度对比 Table 2 Complexity comparison between chaos algorithm and exhaustive method

4 结束语

研究了蜂窝网络中能量效率和服务质量的联合优化问题, 根据能量效率的概念, 结合实际的蜂窝网络中基站与用户终端选择连接的原则, 建立了能量效率与用户终端服务质量联合优化的数学模型。通过基于幂函数载波技术的混沌搜索算法求解数学模型得到最优解或近似最优解, 完成基站与用户终端的连接选择。仿真结果表明, 在一定的中断概率下, 通过求解该模型得到的连接选择下的能量效率优于LRP模型下的连接选择, 同时通过证明混沌搜索算法的收敛性, 也说明了混沌搜索算法求解该类具有约束条件的0-1整数规划优化问题的可行性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	朱近康, 许莉. 绿色蜂窝网络的频谱效率与能效函数[J]. 通信学报, 2013, 34(1): 1-7. Zhu Jin-kang, Xu Li. Green cellular networks spectrum efficiency and the function of energy efficiency[J]. Journal of Communication, 2013, 34(1): 1-7. [本文引用:1]
[2]	Chiaraviglio L, Ciullo D, Marsan M A, et al. Energy-aware UMTS access networks[C]∥Proc of IEEE W-GREEN, Lapland , Finland , 2008: 1-8. [本文引用:2]
[3]	Marsan M A, Chiaraviglio L, Ciullo D, et al. Optimal energy savings in cellular access networks[C]∥Proceedings of the 2009 IEEE International Conference on Communications Workshops. Piscataway: IEEE, 2009: 1-5. [本文引用:2]
[4]	Marsan M A, Meo M. Energy efficient management of two cellular access networks[J]. ACM SIGMETRICS Performance Evaluation Review, 2010, 37(4): 69-73. [本文引用:2]
[5]	Oh E, Krishnamachari B. Energy savings through dynamic base station switching in cellular wireless access networks[C]∥Global Telecommunications Conference (GLOBECOM 2010), Miami, FL, 2010: 1-5. [本文引用:1]
[6]	周旋. 基于能量和频谱效率的移动通信网络重配置[D]. 成都: 电子科技大学通信与信息工程学院, 2013. Zhou Xuan. Mobile communication network reconfiguration based on energy and spectrum efficiency[D]. Chengdu: School of Communication & Information Engineering, University of Electronic Science and Technology, 2013. [本文引用:1]
[7]	Zhu Y, Kang T, Zhang T, et al. QoS-aware user association based on cell zooming for energy efficiency in cellular networks[C]∥Personal, Indoor and Mobile Radio Communications (PIMRC Workshops), London, 2013: 6-10. [本文引用:1]
[8]	李云, 朱雪, 廖超. 蜂窝网络中能效最大的最优中继位置研究[J]. 重庆邮电大学学报: 自然科学版, 2014, 26(1): 25-30. Li Yun, Zhu Xue, Liao Chao. Optimal relays’positions for maximum energy efficiency in cellular networks[J]Journal of Chongqing University of Posts and Telecommunications (Natural Science Edition), 2014, 26(1): 25-30. [本文引用:1]
[9]	祁荣宾, 冯汝鹏. 求解一类0-1整数规划问题的新方法——混沌搜索算法[J]. 控制与决策, 2003, 18(6): 712-715. Qi Rong-bin, Feng Ru-peng. Solving a class of new method of 0-1 integer programming problem—chaotic search algorithm[J]. Control and Decision, 2003, 18(6): 712-715. [本文引用:1]
[10]	桑晓丹, 罗兴国, 禹春来, 等. 求解0-1整数规划问题的混沌遗传算法[J]. 计算机应用研究, 2011, 28(7): 2443-2445. Sang Xiao-dan, Luo Xing-guo, Yu Chun-lai, et al. The chaos genetic algorithm to solve the 0-1 integer programming problem[J]. Application Research of Computers, 2011, 28(7): 2443-2445. [本文引用:1]

2013

0.0

. 2013, 34(1):1-7 DOI:doi:10.3969/j.issn.1000-436x.2013.01.001

Green cellular networks spectrum efficiency and the function of energy efficiency

绿色蜂窝网络的频谱效率与能效函数

Zhu Jin-kang , Xu Li

朱近康, 许莉

为了给绿色蜂窝网络的研究和设计提供一个基本的基准或判断依据,对存在多小区干扰和越区切换情况下蜂窝网络的网络传输能力(网络频谱效率)和能量效率函数(能效函数)进行了研究,揭示了蜂窝网络的功率开销与频谱效率之间的关系。首先,给出了蜂窝网络能效函数的定义,并在此基础上提出了小区干扰深度和越区切换的动力学模型,进而论证了存在多小区干扰和越区切换情况下的蜂窝网络频谱效率,并推证了数学表达式。最后,求解了蜂窝网络的能效函数,讨论了相关参数对它的影响和数值结果分析,为绿色蜂窝网络的研究和设计,提供了有益的分析依据和基础。

... 已成为目前通信领域重要的研究方向,是亟待研究发展的重大前沿课题^[1] ...

2008

0.0

... 在此策略中,如何确定哪些基站进入休眠模式、哪些基站扩大覆盖范围是一个关键问题^[2,3,4,5] ...

... 文献[2]证明了通过基站切换进行节能的可行性 ...

2009

0.0

... 在此策略中,如何确定哪些基站进入休眠模式、哪些基站扩大覆盖范围是一个关键问题^[2,3,4,5] ...

... 文献[3]针对基站不同的关掉比例,采用简化分析方法研究基站切换策略并应用于蜂窝网络,另外,这种方法也考虑了切换前和切换后移动台所归属的两个不同的效用平衡^[4] ...

2010

0.0

... 在此策略中,如何确定哪些基站进入休眠模式、哪些基站扩大覆盖范围是一个关键问题^[2,3,4,5] ...

2010

0.0

... 在此策略中,如何确定哪些基站进入休眠模式、哪些基站扩大覆盖范围是一个关键问题^[2,3,4,5] ...

2013

0.0

. 2013, :-

Mobile communication network reconfiguration based on energy and spectrum efficiency

基于能量和频谱效率的移动通信网络重配置

Zhou Xuan

周旋

传统无线移动通信系统最大化系统的频谱效率，即最大化系统每赫兹带宽每秒所传输的比特数，在本文中被称为频谱效率（Spectral Efficient，SE)系统。SE系统牺牲能量换取系统的频谱效率，同时还存在能量浪费的情况。在通信领域，通信系统设计师也开始将注意力转移到最大化系统的能量效率，即最大化系统每焦耳能量每秒传输的比特数。本文将以能量效率最大化进行设计的系统称为能量效率(Energy Efficient，EE)系统。SE和EE系统都没有考虑到系统业务量发生变化的情况。当系统设计单纯以最大化频谱效率或者能量效率为目标时，若系统业务量变化，将导致较差的系统性能，如中断概率较高，吞吐量较小，频谱效率较低或者能量效率较低等。另外，当前的移动通信系统仍然缺乏对能量和频谱资源进行公平分配的有效机制。因此，本篇论文针对动态业务量变化，围绕频谱效率和能量效率，提出了两种网络重配置的方案，即基于基于排队论的动态业务感知网络重配置方案(Dynamic Traffic-Aware Reconfiguration, DTR)和基于博弈论的网络重配置方案(Game Theoretical Reconfiguration, GTR)。基于排队论的动态业务感知网络重配置方案目标为保证用户服务质量，并最大化系统的平均能量效率。而基于博弈论的网络重配置方案目标为公平分配系统中的频谱资源和能量资源。两种方案具备以下特点：基于排队论的动态业务感知网络重配置方案，动态地根据当前小区内的业务量，通过排队论系统预测系统的中断概率，并根据预测出的系统中断概率将系统重配置为SE系统，EE系统或者是混合SE-EE系统。具体的，当业务量较大，DTR将系统配置为SE系统；当业务量较小，DTR将系统配置为EE系统；而当业务量适中时，DTR将系统配置为混合SE-EE系统。通过LTE系统级仿真发现DTR相对于SE和EE系统，可以最大化系统的平均能量效率，同时保障系统性能。基于博弈论的频谱效率和能量效率重配置方案，根据经典的纳什博弈论理论，对系统中的频谱效率和能量效率进行公平分配的博弈建模，将频谱效率和能量效率分别抽象为虚拟博弈者。通过对频谱效率和能量效率的公平性博弈迭代，本方案可以确定系统的发射功率和调制方案，使得系统中的频谱效率和能量效率处于比例公平状态。该方案采用LTE系统级仿真平台，对比未采用博弈论进行配置的SE，EE系统和GTR方案中能量效率和频谱效率之间的比例公平性。仿真结果显示GTR方案可以保证频谱效率和能量效率之间的比例公平性。

... 1 系统模型本文采用能量效率的通用定义^[6],即:能量效率等于每单位能量传输的数据比特数,考虑到电路损耗,能量效率 ηEE表示为: ...

2013

0.0

... 蜂窝网络中的基站与移动终端之间的连接关系可以用加权二部图来表示,按照二部图的方法可以将蜂窝网络演变成如图1所示的模型^[7,8] ...

2014

0.0

. 2014, 26(1):25-30 DOI:doi:10.3979/j.issn.1673-825X.2014.01.005

Optimal relays#cod#x02019;positions for maximum energy efficiency in cellular networks

蜂窝网络中能效最大的最优中继位置研究

Li Yun , Zhu Xue , Liao Chao

李云, 朱雪, 廖超

在新一代蜂窝网络中,固定中继能够有效提高网络性能.在单小区内考虑上行传输,研究以能效最大化为目标的最优中继位置问题.定义了上行传输能效(uplink energy efficiency,uEE),并分别推导出用户均匀分布下,无中继网络和中继网络的uEE解析表达式.通过分析和仿真,研究中继位置对uEE的影响.结果表明,可以通过优化中继位置获得最大uEE.评估了不同参数,如小区半径、中继数目和用户占用的资源比例对最优中继位置以及最大uEE的影响.

... 蜂窝网络中的基站与移动终端之间的连接关系可以用加权二部图来表示,按照二部图的方法可以将蜂窝网络演变成如图1所示的模型^[7,8] ...

2003

0.0

... 2 改进的混沌搜索算法混沌是非线性系统中较为普遍的一种现象,相应的混沌搜索算法被广泛应用于非线性优化领域^[9] ...

2011

0.0

. 2011, 28(7):2443-2445 DOI:doi:10.3969/j.issn.1001-3695.2011.07.010

The chaos genetic algorithm to solve the 0-1 integer programming problem

求解0-1整数规划问题的混沌遗传算法

Sang Xiao-dan , Luo Xing-guo , Yu Chun-lai

桑晓丹, 罗兴国, 禹春来

针对一类特殊的0-1整数规划求解问题提出一种混沌遗传算法。该算法采用幂函数载波技术提高混沌搜索的充分性与遍历性,以混沌搜索算法得出的优化个体作为遗传算法的新群体进行交叉、变异等操作,提高种群质量,同时增加种群多样性,改善遗传算法的早熟问题。该算法被用于解决片上网络映射A3MAP(architec-ture-aware analytic mapping)0-1整数规划问题。实验仿真证明,该算法的收敛速度和解的精度均优于A3MAP-GA。

... 本文采用基于幂函数载波技术的混沌搜索算法^[10]求解式(9)中的目标函数,具体步骤如下: ...