双基地MIMO雷达的快速测向算法

引用本文

刘声, 杨力生, 殷艳红, 许锦, 曹海林. 双基地MIMO雷达的快速测向算法. 2016, 46(5): 1675-1680
LIU Sheng, YANG Li-sheng, YIN Yan-hong, XU Jin, CAO Hai-lin. Fast direction finding algorithm in bistatic MIMO radar. Journal of Jilin University Engineering and Technology Edition, 2016, 46(5): 1675-1680 复制到剪切板

Permissions

双基地MIMO雷达的快速测向算法

刘声^1,², 杨力生^1,², 殷艳红^1,², 许锦^1,², 曹海林^1,²

1.重庆大学通信工程学院, 重庆 400044

2. 重庆大学飞行器测控与通信教育部重点实验室, 重庆 400044

通信作者:杨力生(1972-),男,教授,博士生导师.研究方向:阵列信号处理.E-mail:ylscqu2615@163.com

作者简介:刘声(1984-),男,博士研究生.研究方向:阵列信号处理.E-mail:gzuliusheng@163.com

基金:国家自然科学基金项目(61301120,61501068); 重庆市自然科学基金项目(CSTC2011GGYS0001)

摘要

提出了一种双基地MIMO雷达的离开角(DOD)和到达角(DOA)的快速估计算法,本算法需要结合已有的测向算法才能完成DOA、DOD的联合估计。首先,利用已有的算法将DOD估计出来。然后,利用已估计出来的DOD将多目标模型分解成多个单目标模型,从而完成DOA的快速估计。在DOA的估计过程中,不需要任何的奇异值分解和谱峰搜索,而且能够实现自动配对。本算法的主要优点是在保证估计精确度的前提下简化原算法,即使在DOD未能被精确估计的前提下,依然能得出比较理想的DOA估计。仿真实验证明了本文算法的有效性。

关键词: 通信技术; 离开角; 到达角; 双基地MIMO雷达; 快速测向

中图分类号:TN957 文献标志码:A 文章编号:1671-5497(2016)05-1675-06

Fast direction finding algorithm in bistatic MIMO radar

LIU Sheng^1,², YANG Li-sheng^1,², YIN Yan-hong^1,², XU Jin^1,², CAO Hai-lin^1,²

1.College of Communication Engineering, Chongqing University, Chongqing 400044, China

2.The Key Laboratory of Aerocraft Tracking Telemetering Command and Communication, Chongqing University, Chongqing 400044, China

Abstract

A fast estimation algorithm for Direction of Departure (DOD) and Direction of Arrival (DOA) in bistatic MIMO radar is proposed. This algorithm should be used in conjunction with an existing algorithm to perform the estimation. First, the DOD is estimated by an existing algorithm. Then the estimated DOD is used to divide the multi-objective model into many single-objective models. Finally, the DOA can be estimated quickly without Singular Value Decomposition (SVD) and peak search. Besides, no pair procedure needs to be implemented in this process. The main advantage of the proposed algorithm is that it can simplify the original algorithm and ensure the estimation accuracy. Simulation results demonstrate the validity of the proposed algorithm.

Keyword: communication technology; direction of departure (DOD); direction of arrival (DOA); bistatic MIMO radar; fast direction finding

Show Figures

0 引言

多输入多输出(Multiple-input multiple-output, MIMO)雷达是利用多元阵列天线同时发送和接收信号的新型雷达系统, 在通信领域里已有了广泛的应用^[1]。MIMO雷达的性能相比于传统的相控阵雷达有着明显的优势, 而对于MIMO雷达的测向研究也成为当前的一个热点问题。Zhang等^[2]提出了一种针对单基地MIMO雷达的降维ESPRIT算法, 从而有效地降低了传统算法的计算复杂度。Li等^[3]将Zhang^[2]的降维思想扩展到二维到达角(DOA)的估计上, 提出一种基于双平行线阵的单基地MIMO雷达的二维DOA估计算法。相比于单基地MIMO雷达, 双基地MIMO雷达的测向需要同时估计离开角(DOD)和DOA。Chen等^{[4, 5]}先后提出了两种基于不同配对思想的ESPRIT算法实现对DOD与DOA的联合估计。Bencheikh等^[6]在Chen^[4]的基础上将ESPRIT算法与MUSIC算法结合在一起提出了一种ESPRIT-MUSIC算法。Xie等^[7]利用Capon算法的原理将DOA、DOD的估计问题转化成一个瑞利方程求解的问题, 并能实现自动配对。Zheng等^[8]利用大孔径阵列提高估计的精确度, 并且使用酉变换来降低计算的复杂度。为了减少计算量, 陈金立等^[9]提出了避免高维特征值分解和谱峰搜索的PM算法。孙中伟等^[10]将PM算法扩展, 提出了一种双基地MIMO雷达的四维角联合估计算法。然而, 这些算法大多数都需要两次计算量较大的估计才能够将DOA和DOD估计出来, 有些算法还需要额外的配对程序。

本文提出一种降低复杂度的算法, 只需使用一种已有的算法就能将DOD估计出来, 再利用已经估计出来的DOD便可将DOA快速估计出来。即便在DOD的估计精确度不高的情况下, 也能得到精确的DOA估计。这种算法可以与各种已有的算法相结合, 降低原算法的计算量, 而且估计性能接近甚至超过原来的算法。

1 双基地MIMO雷达信号模型

考虑一个双基地MIMO雷达系统的发射阵列为 $N$ 元均匀线阵, 接收阵列为 $M$ 元均匀线阵。两个阵列的阵元间隔均为 $d = λ / 2$ , 其中 $λ$ 表示信号的波长。假设目标的数目 $\begin{matrix} K \end{matrix}$ 是已知的, $\begin{matrix} φ_{k} 、 θ_{k} 分别表示第 k \end{matrix}$ 个目标相对发射阵列的离开角和相对接收阵列的到达角, $\begin{matrix} k = 1, 2, \dots, K 。 \end{matrix}$ 发射天线在发送端发射互相正交的窄带波形, 则经过匹配滤波器后, 接收阵列接收到的回波信号可以表示为^{[4, 5, 6, 7, 9]}:

$\begin{matrix} x (t) = C (θ, φ) s (t) + n (t), t = 1, 2 \dots, T (1) \end{matrix}$

式中: $C (θ, φ) = [a_{r} (θ_{1}) \otimes a_{t} (φ_{1}), a_{r} (θ_{2}) \otimes a_{t} (φ_{2}), \dots, a_{r} (θ_{K}) \otimes a_{t} (φ_{K})] \in C^{MN \times K}$ , 其中 $a_{r} (θ_{k}) = [1, e^{- \frac{j 2 πdsin θ_{k}}{λ}}, \dots, e^{- \frac{j 2 π (M - 1) dsin θ_{k}}{λ}}]^{T} \in C^{M \times 1}; a_{t} (φ_{k}) = [1, e^{- \frac{j 2 πdsin φ_{k}}{λ}}, \dots, e^{- \frac{j 2 π (N - 1) dsin φ_{k}}{λ}}]^{T} \in C^{N \times 1}; x (t) = [x_{1} (t), x_{2} (t), \dots, x_{MN} {(t)]}^{T} \in C^{MN \times 1}; s (t) = [s_{1} (t), s_{2} (t), \dots, s_{K} {(t)]}^{T}; n (t) = [n_{1} (t), n_{2} (t), \dots, n_{MN} {(t)]}^{T} \in C^{MN \times 1}$ 表示互不相干的高斯白噪声向量; ⓧ表示Kronecker积。

设协方差矩阵为 $\begin{matrix} R = E [x (t) x^{H} (t)], 则 R \end{matrix}$ 可以由有限次采样数近似估计出来:

$\begin{matrix} R \approx \hat{R} = \frac{1}{T} \overset{T}{\sum_{t = 1}} x (t) x^{H} (t) (2) \end{matrix}$

式中: $\begin{matrix} T \end{matrix}$ 为采样次数。

2 算法描述

首先, 假设DOD已经由已有算法^{[4, 5, 6, 7, 8, 9]}估计出。不妨设 $\begin{matrix} \hat{φ} = [{\hat{φ}}_{d 1}, {\hat{φ}}_{d 2}, \dots, {\hat{φ}}_{dK}], \end{matrix}$ 其中 $\begin{matrix} {\hat{φ}}_{d 1}, {\hat{φ}}_{d 2}, \dots, {\hat{φ}}_{dK} \end{matrix}$ 的排列是任意的, 也就是说 $\begin{matrix} {\hat{φ}}_{dk} \end{matrix}$ 不一定是 $\begin{matrix} φ_{k} \end{matrix}$ 的估计值。然后, 利用已经估计出来的 $\begin{matrix} \hat{φ} \end{matrix}$ 来估计DOA。

令 $\begin{matrix} y (t) = [x_{1} (t), x_{2} (t), \dots, x_{N} {(t)]}^{T} \in C^{N \times 1}, z (t) = {[\begin{matrix} x_{N + 1} (t) & x_{N + 2} (t) & \dots & x_{MN} (t) \end{matrix}]}^{T} \in C^{(M - 1) N \times 1}, \end{matrix}$ 设 $\begin{matrix} R_{1} = E [y (t) z^{H} (t)] (R_{1} \end{matrix}$ 的估计值可从式(2)中直接获得), 因为之前已经假设过不同阵元接收的噪声是不相关的, 所以有:

$\begin{matrix} \begin{matrix} R_{1} = E [y (t) z^{H} (t)] = \\ A_{1} (φ) E [s s^{H}] {A^{H}}_{2} (θ, φ) = \\ A_{1} (φ) S {A^{H}}_{2} (θ, φ) (3) \end{matrix} \end{matrix}$

式中: $A_{1} (φ) = [a_{t} (φ_{1}), a_{t} (φ_{2}), \dots, a_{t} (φ_{K})] \in C^{N \times K}, A_{2} (θ, φ) = [a_{r 2} (θ_{1}) \otimes a_{t} (φ_{1}), a_{r 2} (θ_{2}) \otimes a_{t} (φ_{2})$ , $\dots, a_{r 2} (θ_{K}) \otimes a_{t} (φ_{K})] \in C^{(M - 1) N \times K}, a_{r 2} (θ_{k}) = [e^{- \frac{j 2 πdsin θ_{k}}{λ}}, \dots, e^{- \frac{j 2 π (M - 1) dsin θ_{k}}{λ}}]^{T} \in C^{(M - 1) \times 1}$ , $\begin{matrix} S = diag {p_{1}, p_{2}, \dots, p_{K}} 。 \end{matrix}$

构造互相关矩阵 $\begin{matrix} R_{1} \end{matrix}$ 的一个重要目的就是抑制噪声。只要采样数足够大, 就能够使 $\begin{matrix} R_{1} \end{matrix}$ 的估计值中包含的噪声成分接近零。这种设计的优点是在信噪比较低的情况下对噪声的抑制作用比较突出。但是需要说明的是, 如果采样数过少, 这种设计方法对噪声的拟制作用就会降低。

令 $\begin{matrix} {\hat{A}}_{1} (\hat{φ}) = [a_{t} ({\hat{φ}}_{d 1}), a_{t} ({\hat{φ}}_{d 2}), \dots, a_{t} ({\hat{φ}}_{dK})], \end{matrix}$ 只要DOD估计准确, 则可知 $\begin{matrix} {\hat{A}}_{1} (\hat{φ}) \end{matrix}$ 是一个列满秩矩阵, 从而有:

$\begin{matrix} \begin{matrix} [{\hat{A}}_{1}^{+}]_{i, :} [{\hat{A}}_{1}]_{:, j} = \{\begin{matrix} 0, i \neq j \\ 1, i = j \end{matrix} (4) \\ i, j = 1, 2, \dots, K \end{matrix} \end{matrix}$

式中: $\begin{matrix} {\hat{A}}_{1}^{+} \end{matrix}$ 表示矩阵 $\begin{matrix} {\hat{A}}_{1} \end{matrix}$ 的广义逆; ${[\cdot]}_{i, :} 、 {[\cdot]}_{:, j}$ 分别表示矩阵的第 $i$ 行和第 $\begin{matrix} j \end{matrix}$ 列。

不妨设 $\begin{matrix} {\hat{φ}}_{dk} \end{matrix}$ 是 $\begin{matrix} φ_{m} \end{matrix}$ 的估计值, 即有:

$[{\hat{A}}_{1}]_{:, k} \approx [A_{1}]_{:, m} (5)$

从而有:

$[{\hat{A}}_{1}^{+}]_{k, :} [A_{1}]_{:, j} \approx \{\begin{matrix} 1, j = m \\ 0, j \neq m \end{matrix}$

$j = 1, 2, \dots, K (6)$

根据式(6)可知:

$\begin{matrix} \begin{matrix} [{\hat{A}}_{1}^{+}]_{k, :} R_{1} = [{\hat{A}}_{1}^{+}]_{k, :} A_{1} (φ) S {A^{H}}_{2} (θ, φ) \approx \\ \underset{只有第 m 个元素不为 0}{\underset{︷}{[0, \dots, 1, \dots, 0]}} S {A^{H}}_{2} (θ, φ) = \\ \underset{只有第 m 个元素不为 0}{\underset{︷}{[0, \dots, p_{m}, \dots, 0]}} {A^{H}}_{2} (θ, φ) (7) \end{matrix} \end{matrix}$

由式(7)可得 $\begin{matrix} K \end{matrix}$ 个单目标模型:

$\begin{matrix} [{\hat{A}}_{1}^{+}]_{k, :} R_{1} \approx p_{m} [a_{r 2} (θ_{m}) \otimes a_{t} (φ_{m} {)]}^{H} (8) \end{matrix}$

令 $\begin{matrix} [{\hat{A}}_{1}^{+}]_{k, :} R_{1} = c_{k}, c_{k 1} \end{matrix}$ 表示由 $\begin{matrix} c_{k} 前 (M - 2) N \end{matrix}$ 个分量构成的向量, $\begin{matrix} c_{k 2} \end{matrix}$ 表示由 $\begin{matrix} c_{k} 后 (M - 2) N \end{matrix}$ 个分量构成的向量, 再根据式(8)可得:

$\begin{matrix} c_{k 1} e^{\frac{j 2 πdsin θ_{m}}{λ}} \approx c_{k 2} (9) \end{matrix}$

由式(9)可知:

$\begin{matrix} e^{\frac{j 2 πdsin θ_{m}}{λ}} \approx \frac{1}{(M - 2) N} \overset{(M - 2) N}{\sum_{j = 1}} \frac{[c_{k 2}]_{j}}{[c_{k 1}]_{j}} (10) \end{matrix}$

令 $\begin{matrix} \frac{1}{(M - 2) N} \overset{(M - 2) N}{\sum_{j = 1}} \frac{[c_{k 2}]_{j}}{[c_{k 1}]_{j}} = w_{k}, \end{matrix}$ 由式(10)可得 $\begin{matrix} θ_{m} \end{matrix}$ 的估计值为:

$\begin{matrix} {\hat{θ}}_{m} = \arcsin \{λ \frac{angle {w_{k}}}{2 πd}\} (11) \end{matrix}$

由推导过程可知 $\begin{matrix} {\hat{θ}}_{m} \end{matrix}$ 与 $\begin{matrix} {\hat{φ}}_{dk} \end{matrix}$ 恰好是一组互相匹配的角度。

对于有些算法, 除了要进行两次计算量较大的估计才能将DOA和DOD估计出来, 还需要使用一些配对技巧才能最终实现对DOA、DOD的联合估计。但是, 如果利用本文算法, 只需要使用一次DOD估计算法, DOA便可快速地被估计出来, 且无须担心参数失配的情况出现。

3 复杂度分析

本文算法是需要与已有的算法联合使用才能完成对DOA和DOD的联合估计。现在就以PM算法和ESPRIT算法为例来说明本文算法在计算复杂度上的优势。由文献[9, 11]可知, $\begin{matrix} M \end{matrix}$ 阶矩阵特征值分解的运算量(复数乘法的次数)是 $\begin{matrix} 25 M^{3} \end{matrix}$ , 求特征值的运算量为 $\begin{matrix} 10 M^{3} 。 \end{matrix}$ 在DOD已被PM算法^[9]估计出来后, 继续使用PM算法估计DOA的主要运算量约为 $\begin{matrix} 2 N (M - 1) KT + (2 N (M - 1) - K) K^{2} + 2 K^{3} + 25 N^{3} {(M - 1)}^{3} 。 \end{matrix}$ 而使用本文算法来估计DOA的运算量主要来自 $\begin{matrix} {\hat{A}}_{1}^{+} \end{matrix}$ 的计算和对 $\begin{matrix} R_{1} \end{matrix}$ 的估计, 所以计算量约为 $\begin{matrix} 2 N K^{2} + 2 K^{3} + MN (M - 1) KT 。 \end{matrix}$ 在DOD已被ESPRIT^[4]算法估计出来后, 继续利用ESPRIT算法估计DOA的计算量约为 $\begin{matrix} 2 N (M - 1) K^{2} + 12 K^{3} 。 \end{matrix}$ 而使用本文算法来估计DOA的运算量主要来自 $\begin{matrix} {\hat{A}}_{1}^{+} \end{matrix}$ 的计算, 所以计算量约为 $\begin{matrix} 2 N K^{2} + 2 K^{3} 。 \end{matrix}$ 通过复杂度对比可以发现, 当本文算法与已有的算法配合使用时, 其计算复杂度会降低。

4 实验仿真与结果

通过4组仿真实验来验证本文算法的有效性。双基地MIMO雷达的结构如图1所示, 假设接收阵元数 $M = 10$ 、发射阵元数 $\begin{matrix} N = 10 。 \end{matrix}$ 在本文中, 只比较本文算法结合PM算法与文献[9]中开始所提到的两次PM算法, 而并不是直接与文献[9]中最后提出的简化算法相比较。因为本文的目的是要比较本文所提出的DOA的估计技巧相比于ESPRIT和PM算法的性能差异, 因而在以下的实验3和实验4中假设两次ESPRIT算法和两次PM算法估计出来的DOA和DOD都已被准确配对。

	Figure Option View Download New Window
	图1 双基地MIMO雷达结构Fig.1 Array configuration of bistatic MIMO radar

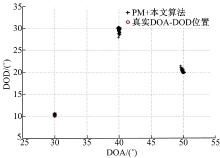
实验1 验证本文算法配合PM算法使用时对DOD、DOA联合估计的效果以及配对情况。设3个目标的DOA、DOD分别为 $\begin{matrix} θ = [30 °, 40 °, 50 °], φ = [10 °, 30 °, 20 °], \end{matrix}$ 信噪比(SNR)为6 dB, 采样数为T=500。100次蒙特卡罗仿真的结果如图2所示。从实验1可以看出, 本文算法能够有效地实现DOA和DOD的自动配对, PM算法估计出来的DOD有一定的偏差。但是, 即使DOD的估计存在偏差, 利用它们所估计出来的DOA却依然十分精确。这说明本文提出的DOA估计算法对DOD的估计有很好的容错性能。

	Figure Option View Download New Window
	图2 实验1估计结果Fig.2 Estimation results of experiment 1

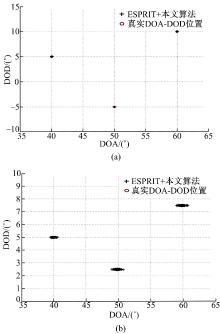
实验2 验证本文算法配合ESPRIT算法使用时对DOD、DOA联合估计的效果以及配对情况。首先, 设3个目标的DOA和DOD分别为 $\begin{matrix} θ = [40 °, 50 °, 60 °], φ = [5 °, - 5 °, 10 °], \end{matrix}$ SNR为10 dB, 采样数为T=500。100次蒙特卡罗仿真的结果如图3(a)所示。将DOD改成 $\begin{matrix} φ = [5 °, 2.5 °, 7.5 °], \end{matrix}$ 其他条件保持不变, 100次蒙特卡罗仿真的结果如图3(b)所示。从图3(a)显示的估计结果可以看出, 本文算法与ESPRIT算法配合使用时有很好的估计效果。但是, 对比图3(a)与图3(b)的结果发现, 当离开角的角度间隔较小时, 算法对DOA的估计会受到影响。

	Figure Option View Download New Window
	图3 实验2估计结果Fig.3 Estimation results of experiment 2

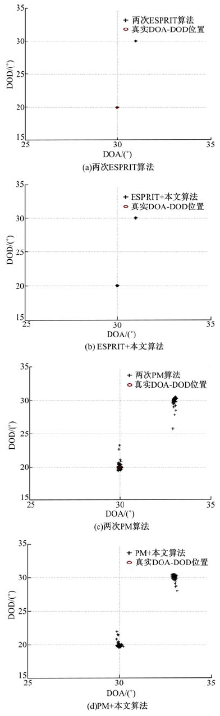
实验3 对比ESPRIT算法加本文算法, PM算法加本文算法, 两次ESPRIT算法以及两次PM算法对角度的分辨能力。事实上, 本文算法只是应用于DOA的估计, 所以仅比较4种算法对DOA的分辨率。首先, 设两个目标的DOD为 $\begin{matrix} φ = [20 °, 30 °], \end{matrix}$ 对于PM算法SNR为6 dB, ESPRIT算法SNR为10 dB, 采样数为T=200。因为PM算法的最小可分辨角度间隔大于ESPRIT算法, 因此对于ESPRIT算法和ESPRIT算法加本文算法取 $\begin{matrix} θ = [30 °, 31 °], \end{matrix}$ 对于PM算法和PM算法加本文算法取 $\begin{matrix} θ = [30 °, 33 °] 。 \end{matrix}$ 4种算法对DOD-DOA的100次联合估计结果如图4所示。对比图4(a)(b)可知, 即使在两个到达角的间隔为 $\begin{matrix} 1 ° \end{matrix}$ 的情况下, 本文算法加ESPRIT算法和ESPRIT算法都能将两个角度清晰地分离开来, 说明在DOD的间隔足够大时, 本文算法和ESPRIT算法配合使用不会降低对DOA的分辨能力。对比图4(c)(d)可知, 两种PM类算法都能分辨两个角度间隔为3° 的到达角, 此时本文算法配合PM算法使用的分辨效果与传统的PM算法接近。

	Figure Option View Download New Window
	图4 实验3估计结果Fig.4 Estimation results of experiment 3

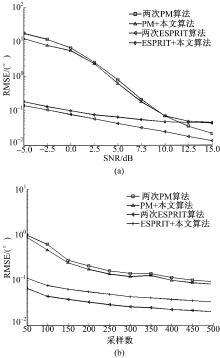
实验4 对比ESPRIT算法加本文算法, PM算法加本文算法, 两次ESPRIT算法以及两次PM算法对DOD、DOA联合估计的精确度。3个目标的DOA、DOD分别固定为 $\begin{matrix} θ = [20 °, 30 °, 40 °], φ = [10 °, 20 °, 30 °] 。 \end{matrix}$ 本文采用均方根误差RMSE来评价估计的精确度:

$\begin{matrix} RMSE = \sqrt{\frac{1}{JK} \overset{K}{\sum_{k = 1}} \overset{J}{\sum_{j = 1}} ({\hat{θ}}_{jk} - θ_{k})^{2} + ({\hat{φ}}_{jk} - φ_{k})^{2}} (12) \end{matrix}$

式中: $J = 500; {\hat{θ}}_{jk} 、 {\hat{φ}}_{jk}$ 分别为在第 $j$ 次实验中对第 $k$ 个目标的DOA和DOD的估计值。

图5(a)给出了采样数固定在200时4种不同算法的估计RMSE随信噪比的变化曲线。图5(b)给出了SNR固定在7.5 dB时4种不同算法的估计RMSE随采样数的变化曲线。从图中可以发现, 本文算法加PM算法的估计效果比使用两次PM算法的效果略好。两次ESPRIT算法的效果要比本文算法加ESPRIT算法的效果略好, 但是前者的计算复杂度明显高于本文算法。除此之外, 从图5(a)还可以看出, 信噪比越低本文算法配合ESPRIT算法的估计效果就会越接近两次ESPRIT算法。从图5(b)可以发现, 4种算法的估计性能随着采样数的减少而降低, 但即使是采样数只有50时, 本文算法也有较好的估计效果。因此, 实验也能说明本文算法对噪声和采样数都有较好的鲁棒性。

	Figure Option View Download New Window
	图5 实验4估计结果Fig.5 Estimation results of experiment 4

5 结束语

提出了一种配合其他算法来降低计算复杂度的双基地MIMO雷达测向算法。算法的主要思想是先利用已有的算法将目标DOD估计出来, 然后利用已估计出来的DOD实现对DOA的快速估计, 而且能使DOA与DOD自动配对。计算复杂度分析和仿真实验表明, 该算法具有较低的计算复杂度和较好的估计精确度。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	高敬鹏, 赵旦峰, 周相超, 等. MIMO-OFDM系统的联合估计检测算法[J]. 吉林大学学报: 工学版, 2014, 44(3): 861-866. Gao Jing-peng, Zhao Dan-feng, Zhou Xiang-chao, et al. Joint estimation and detection algorithm in MIMO-OFDM systems[J]. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(3): 861-866. [本文引用:1]
[2]	Zhang X F, Xu D Z. Low-complexity ESPRIT-based DOA estimation for collocated MIMO radar[J]. Electronic Letters, 2011, 47(4): 283-284. [本文引用:2]
[3]	Li J F, Zhang X F, Chen W Y, et al. Reduced-dimensional ESPRIT for direction finding monostatic MIMO radar with double parallel uniform linear arrays[J]. Wireless Personal Communication, 2014, 77(1): 1-19. [本文引用:1]
[4]	Chen D F, Chen B X, Qin G D. Angle estimation using ESPRIT in MIMO radar[J]. Electronic Letters, 2008, 44(12): 770-771. [本文引用:5]
[5]	Chen J L, Guo H, Su W M. Angle estimation using ESPRIT without pairing in MIMO radar[J]. Electronic Letters, 2008, 44(24): 1422-1423. [本文引用:3]
[6]	Bencheikh M L, Wang Y. Joint DOD-DOA estimation using combined ESPRIT-MUSIC approach in MIMO radar[J]. Electronic Letters, 2010, 46(15): 1081-1083. [本文引用:3]
[7]	Xie R, Liu Z, Wu J X. Direction finding with automatic pairing for bistatic MIMO radar[J]. Signal Processing, 2012, 92(1): 198-203. [本文引用:3]
[8]	Zheng G M, Chen B X. Unitary dual-resolution ESPRIT for joint DOD and DOA estimation in bistatic MIMO radar[J]. Multidimensional System and Signal Processing, 2015, 26(1): 159-178. [本文引用:2]
[9]	陈金立, 顾红, 苏卫民. 一种双基地MIMO雷达快速多目标定位方法[J]. 电子与信息学报, 2009, 31(7): 1664-1668. Chen Jin-li, Gu Hong, Su Wei-min. A method for fast multi-target localization in bistatic MIMO radar system[J]. Journal of Electronics and Information Technology, 2009, 31(7): 1664-1668. [本文引用:7]
[10]	孙中伟, 张小飞, 吴海浪, 等. L型阵列双基地MIMO雷达的传播算子多维角度估计[J]. 应用科学学报, 2014, 32(1): 57-64. Sun Zhong-wei, Zhang Xiao-fei, Wu Hai-lang, et al. Multidimensional angle estimation in bistatic MIMO radar for L-shape array with propagator method[J]. Journal of Applied Sciences, 2014, 32(1): 57-64. [本文引用:1]
[11]	Golub G H, VanLoan C F. Matrix Computations[M]. 3rd ed. Baltimore: John Hopkins University Press, 1996: 359-360. [本文引用:1]

2014

0.0

. 2014, 44(3):861-866 DOI:doi:10.13229/j.cnki.jdxbgxb201403045

Joint estimation and detection algorithm in MIMO-OFDM systems

MIMO-OFDM系统的联合估计检测算法

Gao Jing-peng , Zhao Dan-feng , Zhou Xiang-chao

高敬鹏, 赵旦峰, 周相超

To overcome the disadvantages of high computational complexity of maximum likelihood detection algorithm and the poor performance of the Least Square (LS) channel estimation, a new joint estimation and detection algorithm is proposed. In order to improve the system effectiveness, LS algorithm is applied to initialize channel and Space-alternating Generalized Expectation-maximization (SAGE) algorithm is employed to process channel iterative estimation. The proposed algorithm combines the improved Grover quantum search algorithm in signal detection. Theoretical study and simulation results show that bit error rate performance of proposed algorithm is better than that of traditional joint detection algorithm. Ideal channel estimation under the maximum likelihood algorithm can be approached by the proposed algorithm with low complexity.

针对最大似然检测算法复杂度高,最小二乘信道估计性能较差等缺陷,提出了一种SAGE-IGQS联合估计检测算法,该算法使用LS算法进行信道初始化,采用SAGE算法进行信道迭代估计,并结合改进的Grover量子搜索算法进行信号检测,从而提高了系统的有效性。理论研究和仿真结果表明:该算法在降低系统复杂度的情况下,误比特率性能优于传统的联合检测算法,与理想信道估计下的最大似然检测算法相接近。

... 0 引言多输入多输出(Multiple-input multiple-output,MIMO)雷达是利用多元阵列天线同时发送和接收信号的新型雷达系统,在通信领域里已有了广泛的应用^[1] ...

2011

0.0

... Zhang等^[2]提出了一种针对单基地MIMO雷达的降维ESPRIT算法,从而有效地降低了传统算法的计算复杂度 ...

... Li等^[3]将Zhang^[2]的降维思想扩展到二维到达角(DOA)的估计上,提出一种基于双平行线阵的单基地MIMO雷达的二维DOA估计算法 ...

2014

0.0

... Li等^[3]将Zhang^[2]的降维思想扩展到二维到达角(DOA)的估计上,提出一种基于双平行线阵的单基地MIMO雷达的二维DOA估计算法 ...

2008

0.0

... Chen等^[4,5]先后提出了两种基于不同配对思想的ESPRIT算法实现对DOD与DOA的联合估计 ...

... Bencheikh等^[6]在Chen^[4]的基础上将ESPRIT算法与MUSIC算法结合在一起提出了一种ESPRIT-MUSIC算法 ...

... 发射天线在发送端发射互相正交的窄带波形,则经过匹配滤波器后,接收阵列接收到的回波信号可以表示为^[4,5,6,7,9]: ...

... 2 算法描述首先,假设DOD已经由已有算法^{[4,5,6,7,8,9]}估计出 ...

... 在DOD已被ESPRIT^[4]算法估计出来后,继续利用ESPRIT算法估计DOA的计算量约为 2N(M-1)K2+12K3 ...

2008

0.0

... Chen等^[4,5]先后提出了两种基于不同配对思想的ESPRIT算法实现对DOD与DOA的联合估计 ...

... 发射天线在发送端发射互相正交的窄带波形,则经过匹配滤波器后,接收阵列接收到的回波信号可以表示为^[4,5,6,7,9]: ...

... 2 算法描述首先,假设DOD已经由已有算法^{[4,5,6,7,8,9]}估计出 ...

2010

0.0

... Bencheikh等^[6]在Chen^[4]的基础上将ESPRIT算法与MUSIC算法结合在一起提出了一种ESPRIT-MUSIC算法 ...

... 发射天线在发送端发射互相正交的窄带波形,则经过匹配滤波器后,接收阵列接收到的回波信号可以表示为^[4,5,6,7,9]: ...

... 2 算法描述首先,假设DOD已经由已有算法^{[4,5,6,7,8,9]}估计出 ...

2012

0.0

... Xie等^[7]利用Capon算法的原理将DOA、DOD的估计问题转化成一个瑞利方程求解的问题,并能实现自动配对 ...

... 发射天线在发送端发射互相正交的窄带波形,则经过匹配滤波器后,接收阵列接收到的回波信号可以表示为^[4,5,6,7,9]: ...

... 2 算法描述首先,假设DOD已经由已有算法^{[4,5,6,7,8,9]}估计出 ...

2015

0.0

... Zheng等^[8]利用大孔径阵列提高估计的精确度,并且使用酉变换来降低计算的复杂度 ...

... 2 算法描述首先,假设DOD已经由已有算法^{[4,5,6,7,8,9]}估计出 ...

2009

0.0

. 2009, 31(7):1664-1668

A method for fast multi-target localization in bistatic MIMO radar system

一种双基地MIMO雷达快速多目标定位方法

Chen Jin-li , Gu Hong , Su Wei-min

陈金立, 顾红, 苏卫民

The direction finding cross localization using bistatic MIMO radar system is studied in this paper, and a fast multi-target localization algorithm based on propagator method is proposed. The new method avoids the estimation and SVD (Singular Value Decomposition) of the covariance matrix of the received signals which are the main computational burden in traditional subspace method, and does not need two-dimensional (2-D) spectrum peak searching. Thus, the computational complexity of the proposed algorithm is reduced with the maintenance of good performance for two-dimensional angle estimation. According to the elementary matrix transformation and the tripartite relationship among matrix, the eigenvalue of the matrix and the eigenvector corresponding to the eigenvalue, the estimated parameters of the proposed algorithm are automatically paired with the additional paring computation eliminated. The simulation results demonstrate its effectiveness and robustness.

该文研究了双基地MIMO雷达测向交叉多目标定位方法，提出了一种基于传播算子的双基地MIMO雷达快速多目标定位算法。该方法避免了一般子空间方法中占主要运算量的协方差矩阵估计和奇异值分解，不需要二维谱峰搜索，在保证二维方位角估计性能的基础上，降低了运算复杂度。利用矩阵的初等变换以及矩阵、矩阵特征值和特征值对应的特征向量三者之间的关系，该算法所估计二维方位角参数能自动配对，不需要额外的配对运算。最后仿真结果验证了该算法的有效性。

... 为了减少计算量,陈金立等^[9]提出了避免高维特征值分解和谱峰搜索的PM算法 ...

... 发射天线在发送端发射互相正交的窄带波形,则经过匹配滤波器后,接收阵列接收到的回波信号可以表示为^[4,5,6,7,9]: ...

... 2 算法描述首先,假设DOD已经由已有算法^{[4,5,6,7,8,9]}估计出 ...

... 由文献[9,11]可知, M阶矩阵特征值分解的运算量(复数乘法的次数)是 25M3,求特征值的运算量为 10M3 ...

... 在DOD已被PM算法^[9]估计出来后,继续使用PM算法估计DOA的主要运算量约为 2N(M-1)KT+(2N(M-1)-K)K2+2K3+25N3(M-1)3 ...

... 在本文中,只比较本文算法结合PM算法与文献[9]中开始所提到的两次PM算法,而并不是直接与文献[9]中最后提出的简化算法相比较 ...

2014

0.0

. 2014, 32(1):57-64 DOI:doi:10.3969/j.issn.0255-8297.2014.01.010

Multidimensional angle estimation in bistatic MIMO radar for L-shape array with propagator method

L型阵列双基地MIMO雷达的传播算子多维角度估计

Sun Zhong-wei , Zhang Xiao-fei , Wu Hai-lang

孙中伟, 张小飞, 吴海浪

摘　要：针对空间谱估计算法复杂度高的问题，引入传播算子用于双基地多输入多输出雷达的二维离开角和二维到达角估计．通过信号协方差矩阵求出传播算子，利用传播算子的旋转不变性估计方向矩阵，进而计算离开角和到达角．该算法运算复杂度低，能实现多维角度的自动配对，且在相近角度情况下仍能保持良好的性能．在高信噪比情况下，算法性能接近ESPRIT．此外还推导了角度估计均方误差．仿真结果表明了该算法的有效性．

... 孙中伟等^[10]将PM算法扩展,提出了一种双基地MIMO雷达的四维角联合估计算法 ...

1996

0.0

... 由文献[9,11]可知, M阶矩阵特征值分解的运算量(复数乘法的次数)是 25M3,求特征值的运算量为 10M3 ...