组合成像技术能够为观看者提供具有全彩色和全视差的立体图像, 已成为新一代立体显示技术的重要组成部分之一^{[1, 2, 3, 4, 5]}。目前, 立体元图像阵列的生成方法主要包括计算机模拟采集法^{[6, 7]}和实景采集法^{[8, 9, 10, 11, 12]}, 计算机模拟采集法^{[6, 7]}主要利用基于计算机的三维动画制作软件来模拟真实相机的映射光路, 从而获得虚拟物体的立体元图像阵列, 但是, 该方法的运算量巨大, 且无法生成实际景物的立体元图像阵列, 因此, 实景采集法始终是组合成像技术的首选采集方法。透镜阵列采集法^{[8, 9, 10]}是最直接、简单的实景采集法, 该方法使用相机直接拍摄3D对象透过透镜阵列的立体元图像阵列, 然而, 较低的采集分辨率、狭窄的观看视角以及较小的景深等问题一直制约着透镜阵列采集法的发展。相机阵列采集法^{[11, 12]}在一定程度上弥补了透镜阵列采集法存在的不足, 但随着显示分辨率的不断提高, 相机阵列的规模也在不断扩大, 大规模的相机阵列既昂贵又不便于调节。

针对上述问题, 文献[13]提出了一种离散视点采集结合窗截取的立体元图像阵列的实景采集方法, 该方法只使用一台相机便可以获得较大尺寸拍摄对象的立体元图像阵列, 且生成的立体元图像阵列的显示分辨率可以根据实际需要进行自由调节, 但是, 该方法在生成截取窗时需要精确获得采集平台的相关参数, 对于一组未知采集参数的离散视点图像, 该方法无法进行处理。为此, 本文在文献[13]的基础上, 提出了基于拍摄对象的自适应窗截取算法, 该方法能够在未获得采集平台参数的情况下, 根据拍摄对象在离散视点图像阵列中的成像区域生成对应的截取窗, 获得与文献[13]完全相同的立体元图像阵列, 保证离散视点图像阵列即使在丢失采集平台参数的情况下也可以正常使用, 提高了离散视点图像阵列的通用性以及立体元图像阵列的生成效率。

本文使用与文献[13]相同的离散视点图像采集平台(如图1所示), 主要包括:拍摄对象、相机、垂直标尺以及配有遥控器的3D摄影轨道。在采集过程中, 将相机安装在3D摄影轨道上, 3D摄影轨道可以使相机沿水平方向匀速移动, 实验人员通过遥控器控制轨道的启动和停止。在相机的移动过程中, 使用相机的多张连拍功能拍摄3D对象的离散视点图像。利用垂直标尺和两个三角架, 等间隔地升起或降下3D摄影轨道, 以获得相机在不同高度下拍摄到的图像信息。如图2所示, 拍摄结束后, 将所有离散视点图像按照相机的拍摄位置由低到高、由右到左的顺序排列成一个离散视点图像阵列。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 离散视点图像采集平台Fig.1 Pickup platform of the discrete viewpoint images

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 离散视点图像阵列Fig.2 Discrete viewpoint image array

图2中包含24× 24幅离散视点图像, 图3给出了9幅放大后的图像, 该9幅图像分别来自离散视点图像阵列中第1、12和24行中的第1、12和24列。显然, 随着拍摄位置从右到左的不断变化, 离散视点图像阵列呈现出了玩具卡车从可见到不可见的连续变化过程。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 放大的离散视点图像Fig.3 Magnified discrete viewpoint images

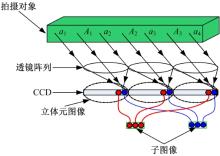
图4为透镜阵列采集法的原理示意图, 当实际物体发出的光线通过透镜阵列投射到电荷耦合元件(Charge-coupled device, CCD)上时, 每个小透镜覆盖范围内的CCD区域便记录了一幅图像信息, 称为立体元图像, 根据立体元图像阵列与子图像阵列间的光学映射关系^[14]可知, 子图像为每幅立体元图像中某一相同位置的像素的集合, 将所有子图像按照组成该子图像的像素点在立体元图像中的位置排列起来, 即得到子图像阵列。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 透镜阵列采集法原理示意图Fig.4 Schematic diagrams of the lenslet-based pickup

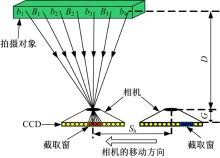
在本文方法中(如图5所示), 用相机在较远处对同一拍摄对象进行离散视点采集, 从图5中可以看出, 采集到的离散视点图像不仅包含对应的子图像, 而且包含了其他像素, 本文的核心思想便是设计一个合适的截取窗, 将每幅子图像从其对应的离散视点图像中截取出来, 并通过逆映射将子图像阵列转换成立体元图像阵列。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 本文方法原理示意图Fig.5 Schematic diagrams of the proposed method

截取窗的参数包括大小、在离散视点图像阵列的第一幅离散视点图像中的初始位置以及在相邻两幅离散视点图像中的相对位移^[13], 文献[13]给出了截取窗参数、离散视点采集平台参数以及透镜阵列采集法的系统参数三者之间的关系, 只要能够设定出合理的截取窗参数的约束条件, 便可以生成符合透镜阵列成像关系的立体元图像阵列。

图6为窗截取算法示意图, 从图中可以看出, 拍摄对象(两辆玩具卡车)是观看者关注的焦点, 为此, 本文提出了基于拍摄对象的自适应窗截取算法, 在对截取窗的参数进行设置时, 自适应地保护拍摄对象的完整性。首先, 计算拍摄对象在离散视点图像阵列中成像区域的变化范围; 然后, 利用拍摄对象在相邻离散视点图像中成像区域的相对位移, 计算截取窗在相邻离散视点图像中的相对位移, 进而得到截取窗的大小和初始位置; 最后, 用计算得到的截取窗对每幅离散视点图像进行截取生成子图像阵列并合成立体元图像阵列。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 窗截取算法示意图Fig.6 Schematic diagrams of the window interception

3.1 计算拍摄对象的成像区域

由图2和图3可知, 拍摄对象的成像区域在属于同一行的离散视点图像中具有相同的上边界和下边界, 在属于同一列的离散视点图像中具有相同的左边界和右边界, 且拍摄对象在离散视点图像阵列的第一行、第一列图像中的成像区域最靠近图像的左上方, 在离散视点图像阵列的最后一行、最后一列图像中的成像区域最靠近图像的右下方, 因此, 只需计算出拍摄对象在该两幅图像中的成像区域范围便可以获得拍摄对象在离散视点图像阵列中成像区域的变化范围。

图7为拍摄对象在第一行、第一列离散视点图像中的成像区域范围计算流程图。首先, 计算离散视点图像阵列的第一行、第一列图像与第一行、第二列图像的灰度图的差值图, 由于相邻两幅离散视点图像的背景信息几乎相同, 因此, 差值图中非零点的区域即为拍摄对象的成像区域, 为了进一步去除背景图像的干扰, 本文对差值图进行滤波处理; 然后, 对滤波后的图像进行边缘检测, 得到差值图的边缘信息, 此时, 边缘信息的上、下和左边界即为拍摄对象在第一行、第一列离散视点图像中成像区域的上、下和左边界, 而边缘信息的右边界却是拍摄对象在第一行、第二列离散视点图像中成像区域的右边界。由于拍摄对象在第一行、第一列离散视点图像中成像区域的右边界可由差值图中边缘信息的右边界减去水平相对位移得到, 因此, 需要计算拍摄对象的成像区域在相邻两幅离散视点图像中的水平相对位移。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 拍摄对象成像区域范围计算流程图Fig.7 Calculation procedure diagram of the imaging area of the object

在计算拍摄对象成像区域的水平相对位移时, 首先, 将第一行、第一列离散视点图像与第一行、第二列离散视点图像重叠放置并计算此时该两幅图像的峰值信噪比; 然后, 将第一行、第一列离散视点图像逐个像素的向右平移, 计算并记录每次平移后两幅图像重叠部分的峰值信噪比, 当完成一定范围的移动后, 峰值信噪比最大时对应的移动距离即为拍摄对象的成像区域在相邻两幅离散视点图像中的水平相对位移。

同理, 可以计算出拍摄对象在离散视点图像阵列的最后一行、最后一列图像中成像区域的范围。

图2中每幅离散视点图像阵列的大小为2592× 1728像素, 由3.1节计算得到拍摄对象在第一行、第一列离散视点图像和最后一行、最后一列离散视点图像中的成像区域范围如表1所示, 拍摄对象的成像区域在水平和垂直相邻两幅离散视点图像中的相对位移分别为41像素和22像素。

表1

Table 1

表1(Table 1)

表1 拍摄对象的成像区域范围 Table 1 Imaging area of the object 像素 离散视点图像 上边界 下边界 左边界 右边界 第一行、第一列 460 800 550 1303 最后一行、最后一列 950 1320 1470 2070

表1 拍摄对象的成像区域范围 Table 1 Imaging area of the object 像素

由式(1)和式(2)可以计算出截取窗的最大水平和垂直相对位移分别为56像素和40像素, 由式(11)可得Δ 的取值范围为0~15像素。当Δ =3像素时, 对应的截取窗的水平和垂直相对位移分别为44像素和25像素。根据显示需要, 设置每幅子图像的分辨率为50× 33像素, 由于截取窗的面积越小, 截取后的子图像中的拍摄对象越大, 越能突出图像的感兴趣区域, 因此, 本文在式(5)和式(6)允许的范围内取截取窗的最小值, 截取窗的宽度和高度分别设为850像素和561像素, 当完成对离散视点图像的截取后, 通过计算截取后图像中每个17× 17像素图像块的像素均值作为子图像中对应位置的像素值的方法实现图像缩小。为了证明本文所提算法能够生成与文献[13]完全相同的立体元图像阵列, 本文设置截取窗的初始位置为(1296, 864), 图8为Δ =3像素时生成的子图像阵列, 从图中可以看出, 生成的子图像阵列具有连续的水平视差和垂直视差。图9为由图8映射得到的立体元图像阵列^[14], 该幅立体元图像阵列的分辨率为1200× 792像素。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 Δ =3时的离散视点图像阵列Fig.8 Discrete viewpoint image array when Δ =3

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 Δ =3时的立体元图像阵列Fig.9 Elemental image array when Δ =3

本文所提算法计算得到的截取窗参数以及生成的立体元图像阵列与文献[13]中的对应数据完全相同。但是, 与文献[13]相比, 首先, 本文的计算过程并未用到离散视点采集平台的任何参数, 而是根据三角测量原理将离散视点采集平台的参数信息通过式(8)转换成了离散视点图像阵列中拍摄对象成像区域的位置信息; 其次, 本文提出了基于拍摄对象完整性的截取窗参数设计原则, 在文献[13]的基础上, 通过式(5)、式(6)、式(12)和式(13)进一步明确了截取窗参数的取值范围, 使截取窗参数的设置更加合理。

与传统方法相比, 本文所提方法具有以下优点:

(1)为了保证立体元图像阵列在显示平台上正常显示, 立体元图像的数量和排列方式必须与显示平台所使用的透镜阵列中小透镜的数量和排列方式完全相同。若要得到能够在不同显示平台上正常显示的多个立体元图像阵列, 在透镜阵列采集法^{[8, 9, 10]}中, 必须使用与所有显示端相匹配的多个透镜阵列进行多次采集, 显然, 这种方法使采集的工作量成倍增长, 同时, 采集端也不可能拥有符合每个显示端透镜阵列参数的所有透镜阵列; 在相机阵列采集法^{[11, 12]}中, 相机阵列中的相机必须按照每个显示端透镜阵列中小透镜的排列方式进行多次排列并采集, 显然这种方法更不现实; 而在本文所提方法中, 根据立体元图像数量与截取窗大小之间的关系, 只需使用不同大小的截取窗对拍摄到的同一组离散视点图像阵列进行截取即可很容易地生成适合不同显示平台的立体元图像阵列。

(2)与相机阵列采集法^{[11, 12]}相比, 本文所提方法可以大大降低拍摄成本和工作量。在相机阵列采集法中, 每个相机采集到的图像为一幅立体元图像; 而在本方法中, 相机在每个拍摄位置采集到的图像对应一幅子图像。若要获得一幅显示分辨率为1024× 768像素, 每幅立体元图像中包含20× 20的立体元图像阵列, 传统相机阵列采集法需要拍摄1024× 768幅图像, 而本方法只需拍摄20× 20幅图像即可。

(3)文献[13]所述方法中, 图像采集端需要将离散视点图像阵列和对应的采集平台参数均传送至显示端, 当采集平台参数丢失时, 显示端即使获得了完整的离散视点图像阵列也无法生成立体元图像阵列; 然而, 本文所提方法能够将一次采集到的离散视点图像阵列处理成适合不同显示平台分辨率的立体元图像阵列, 在实际应用中, 图像采集端只需采集一个离散视点图像阵列并将其发送到显示端, 显示端即可根据自身的显示平台参数生成相应的立体元图像阵列, 由于立体元图像阵列的生成过程无需采集平台参数, 因此, 本文方法提高了离散视点图像阵列的通用性。此外, 当需要批量生成立体元图像阵列时, 采用文献[11]的方法, 操作人员需要在调用每组离散视点图像阵列后输入其对应的采集平台参数, 显然, 这不仅降低了生成效率, 而且还可能引入人为疲劳带来的参数输入错误; 而在本文方法中, 由于截取窗参数是计算机自动生成的, 因此, 本文所提方法提高了立体元图像阵列的生成效率。

提出了一种离散视点采集结合自适应窗截取的立体元图像阵列生成方法, 该方法首先获取拍摄对象的离散视点图像阵列; 然后, 在保护拍摄对象完整性原则的约束下, 利用计算得到的拍摄对象在离散视点图像阵列中成像区域的变化范围, 计算出截取窗参数的取值范围; 最后, 利用生成的截取窗从离散视点图像阵列中获得子图像阵列并转换成立体元图像阵列。实验结果表明, 本文所提方法能够在未获得离散视点采集平台参数的情况下生成与传统方法完全相同的立体元图像阵列, 该方法特别适用于采集与处理过程异步的“ 一次采集— 多次处理” 的广播式立体元图像阵列生成模式。