随着视频监控和目标识别的需求日益增长, 视频图像中显著目标的检测与提取变得越来越重要。在过去的数十年中, 受人类视觉注意机制的启发, 许多针对显著目标提取的视觉显著性模型被提出。首个显著性模型由Itti和Koch等^{[1, 2]}基于Treisman的特征整合理论(Feature integration theory, FIT)^{[3, 4]}提出, 该模型在不同尺度下利用中央周边差算子融合不同的图像初级视觉特征, 如颜色、亮度、朝向等。此后, 许多研究人员做了大量工作来改进Itti的模型。例如, Harel等^[5]提出了一种基于图论的视觉显著性算法(Graph-based visual saliency, GBVS), Hou等^[6]于2007年提出了谱残差方法(Spectral residual, SR), Li等^[7]提出了基于超复数傅里叶变换(Hyper-complex Fourier transform, HFT)的计算模型。上述算法在检测显著性目标时都取得了较好的效果, 然而, 它们通常不能像人类视觉系统一样得到显著目标的准确位置, 且其定位位置也与目标的实际大小不相符。相较于场景中频繁出现的特征, 人类的视觉注意更容易被那些稀有并且具有区别性的特征所吸引。据此, 本文提出一种基于快速字典学习与特征稀有性的自然图像显著目标提取算法(Fast dictionary learning and feature rarity based salient object extraction, FR-SOE), 实验结果表明, 本文所提算法相较于其他4种现存的传统算法提取自然图像中的显著目标更为准确, 并能够有效地处理包含多个显著目标的自然图像。

稀疏编码^{[8, 9]}是一种模拟哺乳动物视觉系统中主视觉皮层V1区简单细胞感受野的人工神经网络方法, 它具有空间的局部性、方向性以及频域的带通性, 是一种自适应的图像统计方法。在数学上, 稀疏编码则是一种多维数据描述方法, 数据在经过稀疏编码之后仅有少数分量同时处于明显的激活状态, 这大致等价于编码后的分量呈现超高斯分布。稀疏编码认为图像可以看成为多个基函数的线性组合, 如图1所示。若有包含 K个原子的过完备字典矩阵 D∈Rn×K,假设输入信号 Y∈Rn可用这些原子的稀疏线性组合进行表示^[10], 则 Y的表示如式(1)所示:

Y=Dx or Y≈Dx1

式中:向量 x∈RK为 Y的表示系数。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 稀疏编码算法Fig.1 Sparse coding algorithm

通过引入稀疏性, 则可求取最优解:

minx‖x‖0, s.t.‖Y-Dx‖2≤ε2

式中: ε为无穷小量。

对于式(2)的求解大多是利用“ 追踪算法” 来求取近似解, 常用的“ 追踪算法” 主要包括匹配追踪(Matching pursuit, MP)^[11]、正交匹配追踪(Orthogonal matching pursuit, OMP)^[12]等。这些算法计算均较为简单, 但由于是零范数约束, 因而优化问题不存在全局最优解。而在2001年, Chen等^[13]证明了在非常稀疏的条件下, l0范数的约束能够由 l1范数的约束来代替, 从而使得稀疏编码实现了快速的发展。目前, l1范数约束的稀疏编码主要包括以下3种形式:

min‖x‖1, s.t.‖Y-Dx‖22≤ε3min‖Y-Dx‖22, s.t.‖x‖1≤λ4min‖Y-Dx‖22+2α‖x‖15

式中: λ为常量; α为调整 x稀疏度的系数。

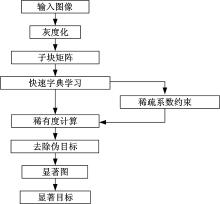
本文通过结合人类视觉感知与视觉注意机制, 提出了FR-SOE算法, 算法框图如图2所示。首先基于稀疏编码理论提出快速字典学习算法应用于提取自然图像的稀疏特征, 然后基于特征稀有性进行显著度计算, 并采用数学形态学算子等方法去除伪目标。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 本文算法框图Fig.2 Block diagram of the proposed algorithm

2.1 快速字典学习算法

假设 Y={y1, y2, …, yN}∈Rn×N表示 N个子图像块的输入特征矩阵, yi∈Rn×1(i=1, 2, …, N)代表 ith子块, X∈RK×N表示与字典 D∈Rn×K相应的稀疏系数矩阵, 其中, K为字典原子个数。则稀疏系数矩阵 X以及字典 D可通过解决式(6)的优化问题^[14]得到:

minX, D‖Y-DX‖F2+2α∑n=1N‖X∙n‖1s.t.‖D∙i‖2≤1, i=1, 2, …, K6

式中: ∙‖F2为Frobenius范数; X∙n为矩阵 X的 nth列。

式(6)若不加约束, 则字典原子可无限大, 从而导致该式无意义。值得注意的是, 在实际推导过程中, 将字典原子约束为小于等于1等同于等于1。上述优化问题可分解为两个交替的优化子问题:①稀疏编码阶段, 即以固定 D的优化; ②字典学习阶段, 即以固定 X的优化。目前, 获取过完备字典的方法很多, 但大多数方法较为耗时, 其中, K-SVD算法^[10]是较有代表性的稀疏编码算法, 但它可能无法得到全局最优解, 并且算法不能保证收敛; FS-LD算法^[14]速度虽然较快, 但会涉及到大规模矩阵求逆的问题, 尤其是当编码特别稀疏时, 有可能出现伪逆的情况。因此, 快速字典学习算法(Fast dictionary learning, FDL)被提出用来解决上述问题, 其目标函数定义如下:

fD, X=‖Y-DX‖F2+2α∑n=1N‖X∙n‖1s.t.‖D∙i‖2=1, ∀i=1, 2, …, K7

式中: X∙n为矩阵 X的 nth列; D∙i为矩阵 D的 ith列; D和 X是非凸的, 但如果固定 D,则对于 X为凸的; 固定 X,则对于 D为凸的。

将式(7)分解为求解稀疏编码目标优化问题以及学习基矩阵目标优化问题, 分别为:

minfX=‖Y-DX‖F2+2α∑n=1N‖X∙n‖18minfD=‖Y-DX‖F2, s.t.‖D∙i‖2=1∀i=1, 2, …, K9

应用块坐标下降方法^{[15, 16]}求解上述优化问题, 从而将寻找稀疏编码优化问题按行分解成一系列的子优化问题, 将学习基矩阵优化问题按列分解成一系列子优化问题。对于每个子优化问题, 可根据抛物线函数的凸性和单调性直接求出使目标函数最小化的闭式解, 而不需要多次迭代。FDL算法每次能够更新 X的一行或是 D的一列, 其更新速度依赖于字典的大小, 此外, 对于大规模特征矩阵, 可通过并行处理来最小化运算时间。

假设 I∈RK×K为单位矩阵, E∈RK×K为元素均为1的方阵, 且Θ 表示点乘, 则FDL算法具体如下:

Step 1 初始化字典 D并且置迭代次数为0, 即 iter=0,同时在字典初始化中减去常数0.5, 使得字典有正有负, 从而保证字典原子的多样性。

D=rand(n, K)-0.5,

D∙k=D∙k‖D∙k‖2, ∀k∈{1, 2, …, K},

X=zerosK, N.

Step 2 更新稀疏系数矩阵 X。

iter=iter+1,

A=DTDΘE-I,

B=DTY.

For k=1; k≤K; k++

XkM=max{BkM-Ak∙X∙M, α}+min{BkM-Ak∙X∙M, -α}

End for

Step 3 更新字典 D。

G=XXTΘE-I.

For k=1; k≤K; k++

D∙k=W∙k-DG∙k‖W∙k-DG∙k‖2

End for

Step 4 更新目标函数。

f=‖Y-DX‖F2+2α∑n=1N‖X∙n‖1.

Step 5 若 (f(iter)-f(iter+1))/f(iter)> 1×10-5,转至Step 2; 否则, 停止迭代并输出 D、X。

本文从MSRA数据库^[17]中随机选取10幅不同大小的自然图像用来验证所提FDL算法的效率, 并与目前广泛应用的K-SVD以及FS-LD算法进行比较。实验图像大小分别为([400× 300]、[400× 320]、[400× 322]、[400× 300]、[373× 400]、[400× 267]、[400× 300]、[400× 320]、[338× 400]、[400× 259]), 字典原子个数 K设为150, 其对比结果如图3所示。观察图3可知, FDL算法所消耗的时间较少, 效率更高。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 算法时间对比图Fig.3 Elapsed time comparison

2.2 基于特征稀有性的显著度计算

自然图像中能够吸引人类视觉注意的区域通常是特征不同于其他场景区域的部分, 即特征为稀有的, 因此稀有性可被用来衡量视觉显著性^{[18, 19]}。基于此, 特征在整幅图像中出现的数量可被认作为特征的稀有性。本文将字典原子在子图像块中出现的频率作为稀有性的度量, 并将其定义为稀有度。频率越高则意味着稀有性越小, 如果一个字典原子在图像块中经常出现, 则其所代表的特征稀有性较低。此外, 据相关研究表明^[20], 如果图像子块中包含目标, 则其在字典下的表示系数是稀疏的, 即只有少量系数值较大, 其他值均较小; 而如果图像子块为背景, 则其在字典下的表示系数为均匀分布, 且每一个系数值均非常小。由于图像子块是否包含目标, 其在字典中的表示系数有着显著的差异, 因此, 本文将稀疏表示系数作为约束条件进行稀有度的计算, 以在一定程度上去除背景环境中噪声干扰等影响。

定义 R=R1R2…RKT作为字典原子的稀有性度量, Ri表示 ith字典原子的稀有度, X为稀疏系数矩阵, 则 ith字典原子的稀有度如式(10)所示:

Ri=1, max(Xi∙)≤τmiS2, max(Xi∙)> τ10

式中: mi为 X的第 ith行的非零系数数量; S为非零系数的总数; Xi∙表示稀疏系数矩阵 X第 ith行的表示系数; τ为阈值。

基于上述运算, 得到各像素的稀有度, 进而应用如图4所示的Sigmoid神经网络函数进行稀有度的变换 f:RR~得到 R~=fR,并更新系数矩阵 X,如式(11)所示:

XU=diagR~×X11

式中: diag(R~)为 R~i的对角线矩阵。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 Sigmoid函数Fig.4 Sigmoid function

图像的显著度图可由式(12)、式(13)计算得到:

YM(x, y)=D×XXU12YS(x, y)=1, YMx, y≥T0, YMx, y< T13

式中: YS为二值化显著度图; T为阈值。

由于自然图像通常背景复杂且干扰因素较多, 而二值化显著图像中孤立的像素点或较小的块并无意义, 因此, 可通过数学形态学算子以及去除较小连通域的方法去除伪目标, 从而得到最终的显著图以及提取目标。数学形态学算子包括膨胀、腐蚀、开运算以及闭运算等, 开运算与闭运算多被用来消噪, 因此, 本文采用开运算以及闭运算来去除噪声等不确定性因素的影响。经形态学处理后, 进一步通过去除较小连通域的方法来改进显著目标提取结果, 如式(14)所示:

Area< ω14

式中: ω为阈值, 采用像素点的8邻域进行计算。

为了验证所提FR-SOE算法的有效性, 应用公开的MSRA显著目标图像库进行实验验证。MSRA数据库由Liu等^[21]建立, 涵盖有多种场景, 并且具有较为明确的显著目标, 因此, 多被算法用以验证显著目标的检测以及提取效果。本文实验基准图来源于Achanta^[22]数据库, Achanta等对来源于MSRA数据库中的部分图像采用手动分割的方法得到基准图, 这些基准图不仅准确并且能够使得多个目标得到有效区分。所有实验均在64位Windows 7系统下进行, 计算机配置Intel 2.5 GHz处理器, 2GB RAM, MATLAB R2012a软件平台。

如前所述, 参数 α用于调整矩阵 X的稀疏度, α越大, 则矩阵 X越稀疏。Yang等^[23]指出 α的经验参数为0.15~0.2, 在本文中, 将其设置为0.2。同时, 本文对不同 K值目标提取结果进行了对比, 如图5所示, 若 K值较小, 则特征信息量较少, 从而目标提取结果不够准确。此外, 由于FDL算法的运行速度依赖于字典的大小, 因此, 综合考虑准确性以及算法效率本文后续实验中取 K=1000。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 不同K值目标提取结果Fig.5 Extraction results with different K

图6中, (a)为原始图像, (b)为基准图, (c)与(d)分别为本文FR-SOE算法所得显著图以及最终提取的目标。此外, 将本文算法与其他4种已有的算法进行了比较, Itti模型、GBVS算法、SR算法以及HFT算法的结果分别如图6(e)、(f)、(g)、(h)所示。观察图6的各子图像可知, Itti等方法均能够在显著图中正确地标示显著目标, 但其大小和轮廓线不能很好地与其实际情况相符合, 而FR-SOE算法则可以得到更为准确的显著目标形状和大小。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 单显著目标提取实例一Fig.6 The first experiment results on single salient object extraction

图7是另一个单显著目标提取实例。与图6类似, 图7中(a)为原始图像, (b)为基准图, (c)与(d)分别为本文FR-SOE算法所得显著图以及最终提取的目标, 图7(e)、(f)、(g)、(h)分别给出了Itti模型、GBVS算法、SR算法以及HFT算法的实验结果。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 单显著目标提取实例二Fig.7 The second experimental results on single salient object extraction

由图7可以看出, SR以及HFT方法均难以较为完整地提取目标, Itti以及GBVS方法则提取不准确, 而本文FR-SOE算法则较为完整而准确地提取出了自然图像中的显著目标。

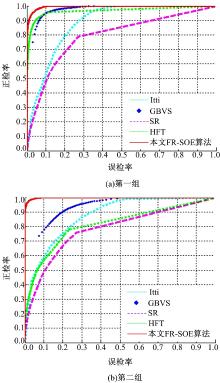
采用受试者工作特性(Receive operating characteristic, ROC)曲线^[7]量化实验结果以便得到更为直观的说明。定义正检点(True positive, TP)为属于显著图目标并且属于基准图目标的像素点, 误检点(False positive, FP)为属于显著图目标但不属于基准图目标的像素点, 图8为上述两组实验中5种不同算法的ROC曲线。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 单目标提取不同算法的ROC曲线图Fig.8 ROC curves of different methods for single object extraction

图8(a)(b)分别为单目标第一组和第二组实验所对应的5种不同算法的ROC曲线图。观察图8可知, 本文所提FR-SOE算法的ROC曲线正检率最高, 其线下面积(Area under curve, AUC)接近于1, 明显优于其他计算模型。

图9列举了部分其他自然图像的实验结果, 对比结果可看出, 较之另外4种算法, 本文算法能够得到更准确的显著目标形状和大小。将本文FR-SOE算法进一步应用于多个显著目标的提取中, 部分结果如图10和图11所示。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 部分单显著目标提取实验结果Fig.9 Some results of single salient object extraction

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 多显著目标提取实例一Fig.10 The first experimental results on multiple salient objects extraction

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 多显著目标提取实例二Fig.11 The second experimental results on multiple salient objects extraction

图10和图11中, (a)为原始图像, (b)为基准图, (c)与(d)分别为本文FR-SOE算法所得显著图以及最终提取的目标, Itti模型、GBVS算法、SR算法以及HFT算法的结果分别如(e)、(f)、(g)、(h)所示。由上述实验结果可以看出, SR算法难以完整地提取图像中的显著目标, Itti算法、GBVS算法以及HFT算法则将两个目标混合为一体, 而本文FR-SOE方法则能够有效地区分每一个显著目标, 得到的显著目标形状和大小更为准确。

图12(a)(b)分别为多目标第一组和第二组实验所对应的ROC曲线图。由图12可知, 本文FR-SOE算法要明显优于其他4种计算模型。图13列举了部分其他包含多个目标的自然图像实验结果, 可见FR-SOE算法能够得到更为准确的显著目标形状及大小, 并且可以有效地区分多个显著目标, 提取效果优于其他4种算法。

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 多目标不同算法的ROC曲线图Fig.12 ROC curves of different methods for multi-object extraction

图13

Fig.13

	Figure Option ViewDownloadNew Window
	图13 部分多目标提取实验结果Fig.13 Some results of multiple salient objects extraction

受稀疏编码和人类视觉注意机制的启发, 提出一种基于快速字典学习与特征稀有性的自然图像显著目标提取算法, 其关键点在于将快速字典学习应用于自然图像稀疏特征提取过程并通过字典原子的稀疏性操作来进行稀有性量化。实验结果表明, 算法对自然图像的显著目标提取效果相较于传统算法提取显著目标更加准确, 速度更快, 并且能够有效地处理含有多个显著目标的自然图像。当然, 本文对于具有特别复杂背景的显著目标提取以及大显著目标的提取效果还不是很理想, 需要今后进一步研究。