五棱台式全张量磁梯度探头侧面倾角优化方法

引用本文

申茂冬, 程德福, 安战峰, 王一, 赵静. 五棱台式全张量磁梯度探头侧面倾角优化方法. 2016, 46(5): 1732-1738
SHEN Mao-dong, CHENG De-fu, AN Zhan-feng, WANG Yi, ZHAO Jing. Optimization of slanting surfaces of five-sided pyramidal full tensor magnetic gradient probe. Journal of Jilin University Engineering and Technology Edition, 2016, 46(5): 1732-1738 复制到剪切板

Permissions

五棱台式全张量磁梯度探头侧面倾角优化方法

申茂冬¹, 程德福¹, 安战峰², 王一¹, 赵静¹

1.吉林大学仪器科学与电气工程学院, 长春 130061

2.中国国土资源航空物探遥感中心, 北京 100083

通信作者:赵静(1982-),男,讲师,博士研究生.研究方向:高温超导磁测技术,弱磁信号测量.E-mail:zhaojing_8239@jlu.edu.cn

作者简介:申茂冬(1988-),男,博士研究生.研究方向:弱磁信号检测.E-mail:shen_dong@sina.cn

基金:“863”国家高技术研究发展计划项目(2013AA063901)

摘要

提出一种五棱台式测量探头侧面倾角的优化方法,通过量化磁梯度张量各独立分量的相对分辨率与探头侧面倾角之间的关系,以5个独立分量相对分辨率的极差与最大值为评估标准,得出五棱台式探头的侧面最优倾斜角度。最后,通过仿真量化了棱台侧面倾角误差对测量结果的影响,为棱台的加工工艺明确了精度要求。

关键词: 仪器仪表技术; 全张量磁梯度探头; 侧面倾角优化; 相对分辨率

中图分类号:TH762 文献标志码:A 文章编号:1671-5497(2016)05-1732-07

Optimization of slanting surfaces of five-sided pyramidal full tensor magnetic gradient probe

SHEN Mao-dong¹, CHENG De-fu¹, AN Zhan-feng², WANG Yi¹, ZHAO Jing¹

1.College of Instrumentation and Electrical Engineering,Jilin University,Changchun 130061,China

2.China Aero Geophysical Survey and Remote Sensing Center for Land and Resources,Beijing 100083, China

Abstract

This paper presents a optimization method of slanting surfaces of a five-sided pyramidal probe based on quantified relations between the relative resolution of each magnetic gradient tensor's independent component and inclination of the probe. The optimal inclination was chosen on the basis of the range and maximum value of the five relative resolutions of the independent components. Finally, simulation results quantify the influence of surface tilt error on the measurement results, and identify the processing accuracy of the probe.

Keyword: technology of instrument and meter; full tensor magnetic gradient probe; optimization of the sloping surface's inclination; relative resolution

Show Figures

航空全张量磁梯度测量是最新一代的航磁测量技术, 由于其测量对象受地磁场的倾角、偏角影响小, 由磁梯度张量计算得到的张量不变量不需额外处理即可很好地描述磁场源, 磁梯度张量反演能够高质量地描述场源体的磁化方向和几何形态(如倾向、走向等), 提高了对磁源体的分辨率, 因此, 在航磁测量中具有不可比拟的优势, 成为国内外航空磁法勘探与军事探潜等领域的一个研究热点^{[1, 2]}。

可构成全张量磁梯度测量系统的磁传感器主要有磁通门与基于超导量子干涉器(Supercon-ducting quantum interference devices, SQUID)的磁强计、轴向磁梯度传感器和平面磁梯度传感器^{[3, 4, 5, 6]}。其中, 轴向超导磁梯度传感器和平面超导磁梯度传感器对共模磁场有很强的抑制能力, 可有效避免运动测量时背景磁场对目标磁场的干扰。与轴向超导磁梯度传感器相比, 平面超导磁梯度传感器体积小、结构简单、一致性较高、便于集成全张量磁梯度测量探头, 更符合航磁测量设备小型化、低功耗、高精度的要求。因此, 多个国家正在积极研制基于平面超导磁梯度传感器的航空超导全张量磁梯度测量系统, 德国耶拿物理高技术研究所已研制出全球唯一一套实用化的全张量磁梯度测量系统^{[7, 8, 9]}。

超导全张量磁梯度测量系统中, 利用5个平面超导磁梯度传感器构建成五棱台式张量测量探头^[7]。探头的侧面倾角决定着平面超导磁梯度传感器在磁梯度张量各分量方向上的拾取环投影面积与基线投影长度, 进而影响所测磁梯度张量的分辨率。本文通过量化分析磁梯度张量各独立分量的相对分辨率, 提出一种探头侧面倾角的优化方法。

1 全张量磁梯度测量原理

1.1 磁梯度张量

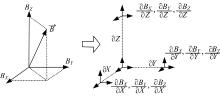
图1为磁梯度张量分量解析图, 由图可知, 磁场强度 $\begin{matrix} \vec{B} \end{matrix}$ 的3个分量(B_X B_Y B_Z)在空间中3个方向(X Y Z)上的变化率构成磁梯度张量T^[10], 表示为:

T= $\begin{matrix} (\begin{matrix} \frac{\partial}{\partial X} \\ \frac{\partial}{\partial Y} \\ \frac{\partial}{\partial Z} \end{matrix}) \end{matrix} \begin{matrix} (B_{X} B_{Y} B_{Z}) \end{matrix}$ = $\begin{matrix} (\begin{matrix} B_{XX} B_{YX} B_{ZX} \\ B_{XY} B_{YY} B_{ZY} \\ B_{XZ} B_{YZ} B_{ZZ} \end{matrix}) \end{matrix}$ (1)

由麦克斯韦方程组可知, 在无源空间中, 磁场强度的旋度和散度均为0, 即:

$\begin{matrix} \begin{matrix} \nabla \times \vec{B} = 0 (2) \\ \nabla \cdot \vec{B} = \frac{\partial B_{X}}{\partial X} + \frac{\partial B_{Y}}{\partial Y} + \frac{\partial B_{Z}}{\partial Z} = 0 (3) \end{matrix} \end{matrix}$

由式(2)得:B_XY=B_YX, B_XZ=B_ZX, B_YZ=B_ZY; 由式(3)得:B_ZZ=-B_XX-B_YY。因此, 式(1)可化简为:

$\begin{matrix} T = (\begin{matrix} B_{XX} B_{YX} B_{ZX} \\ B_{XY} B_{YY} B_{ZY} \\ B_{XZ} B_{YZ} B_{ZZ} \end{matrix}) = (\begin{matrix} B_{XX} & B_{XY} & B_{XZ} \\ B_{XY} & B_{YY} & B_{YZ} \\ B_{XZ} & B_{YZ} & - B_{XX} - B_{YY} \end{matrix}) (4) \end{matrix}$

由式(4)可知, 磁梯度张量的9个分量中, 只有5个分量是独立的, 通过测量该5个分量即可获得磁场一阶梯度张量的所有信息。

	Figure Option View Download New Window
	图1 磁梯度张量分量解析图Fig.1 Analysis diagram of magnetic gradient tensor components

1.2 平面超导磁梯度传感器

图2为平面超导磁梯度传感器结构示意图, 该传感器主要由SQUID磁强计、耦合线圈及拾取环等部件组成^[11]。其中, SQUID磁强计通过耦合线圈读取两个拾取环中的磁通差, 进而得到磁场基于平面磁梯度传感器坐标系的梯度值G。

	Figure Option View Download New Window
	图2 平面超导磁梯度传感器示意图Fig.2 Schematic diagram of planar superconducting magnetic gradient sensor

在平面磁梯度传感器坐标系中, xoy面为传感器所在平面, x轴向为基线方向, z轴垂直于传感器平面向上。平面超导磁梯度传感器测量的磁梯度值G表示为:

$\begin{matrix} G = \frac{\partial^{2} U}{\partial x \partial z} = \frac{\partial B_{Z}}{\partial x} = κ \cdot V_{out} (5) \end{matrix}$

式中:U为平面磁梯度传感器处的标量磁位; κ 为平面磁梯度传感器的磁梯度(电压比例系数); V_out为平面磁梯度传感器的输出电压。

将5个平面超导磁梯度传感器搭建成正五棱台结构的张量探头^[7], 利用5个平面磁梯度传感器的测量值可求得磁梯度张量的5个独立分量。

1.3 五棱台式全张量磁梯度测量探头

图3为正五棱台式探头结构示意图, 其中5个平面磁梯度传感器布置于探头的5个侧面上, 且传感器的基线方向与所在侧面上、下底边的中点连线平行。

	Figure Option View Download New Window
	图3 五棱台式探头结构示意图Fig.3 Schematic diagram of five-sided pyramidal probe

图3中∑ (O-X, Y, Z)为探头坐标系, XOY面为棱台底面, 原点O为棱台底面中心, X轴为1#与5#梯度传感器中间的棱线在底面上的投影, Z轴垂直向上。

设平面磁梯度传感器坐标系的x_io_iy_i面(下标i为梯度传感器编号)与XOY面的夹角为θ _i, x_i轴在XOY面上的投影与X轴的夹角为φ _i, 则探头坐标系与各平面磁梯度传感器坐标系的对应关系为:

$\begin{matrix} \{\begin{matrix} X = x_{i} \cos φ_{i} \sin θ_{i} - y_{i} \sin φ_{i} + z_{i} \cos φ_{i} \cos θ_{i} \\ Y = x_{i} \sin φ_{i} \sin θ_{i} + y_{i} \cos φ_{i} + z_{i} \sin φ_{i} \cos θ_{i} \\ Z = x_{i} \cos θ_{i} - z_{i} \sin θ_{i} \end{matrix} (6) \end{matrix}$

由式(5)(6)可得张量探头上各平面磁梯度传感器的测量值与5个独立分量的关系式:

$\begin{matrix} \begin{matrix} G_{i} = \frac{\partial^{2} U}{\partial x_{i} \partial z_{i}} = \\ \frac{\partial}{\partial x_{i}} (\frac{\partial U}{\partial X} \cdot \frac{\partial X}{\partial z_{i}} + \frac{\partial U}{\partial Y} \cdot \frac{\partial Y}{\partial z_{i}} + \frac{\partial U}{\partial Z} \cdot \frac{\partial Z}{\partial z_{i}}) = \\ \frac{\partial}{\partial x_{i}} (\cos φ_{i} \cos θ_{i} \cdot B_{X} + \sin φ_{i} \cos θ_{i} \cdot B_{Y} - \\ \sin θ_{i} \cdot B_{Z}) = \frac{(1 + co s^{2} φ_{i}) \sin 2 θ_{i}}{2} B_{XX} + \\ \frac{(1 + si n^{2} φ_{i}) \sin 2 θ_{i}}{2} B_{YY} + \frac{\sin 2 φ_{i} \sin 2 θ_{i}}{2} B_{XY} + \\ \cos φ_{i} \cos 2 θ_{i} \cdot B_{XZ} + \sin φ_{i} \cos 2 θ_{i} \cdot B_{YZ} (7) \end{matrix} \end{matrix}$

由式(7)可知, 5个平面磁梯度传感器的测量值与其传感器在探头上的角度参数可构成关于5个独立分量的五元一次方程, 联立成方程组后得到基于探头坐标系的5个独立分量值, 表示为:

$\begin{matrix} (\begin{matrix} B_{XX} \\ B_{YY} \\ B_{XY} \\ B_{XZ} \\ B_{YZ} \end{matrix}) = M^{- 1} \cdot (\begin{matrix} G_{1} \\ G_{2} \\ G_{3} \\ G_{4} \\ G_{5} \end{matrix}) (8) \end{matrix}$

式中:M为5× 5矩阵, 行分量为各平面磁梯度传感器基于探头坐标系的角度参数向量:

$\begin{matrix} {[\begin{matrix} (1 + co s^{2} φ_{i}) \sin 2 θ_{i} / 2 \\ (1 + si n^{2} φ_{i}) \sin 2 θ_{i} / 2 \\ \sin 2 φ_{i} \sin 2 θ_{i} / 2 \\ \cos φ_{i} \cos 2 θ_{i} \\ \sin φ_{i} \cos 2 θ_{i} \end{matrix}]}^{T} \end{matrix}$ 。

2 五棱台式探头侧面倾角优化

2.1 磁梯度张量各独立分量的分辨率

由式(8)可知, 磁梯度张量的5个独立分量与5个平面磁梯度传感器的测量值线性相关, 因此, 各独立分量的微弱变化可利用各平面磁梯度传感器测量值的变化量求得。例如, 计算B_XX的微小变化量dB_XX:

$\begin{matrix} \{\begin{matrix} d B_{XX} = \overset{5}{\sum_{i = 1}} \frac{\partial B_{XX}}{\partial G_{i}} d G_{i} \\ d G_{i} = n_{i} \cdot R_{i} \end{matrix} (9) \end{matrix}$

式中:n_i为整数; R_i为各平面磁梯度传感器的分辨率(i为梯度传感器编号)。

式(9)中, 由于5个平面梯度传感器之间相互独立, 当n_i中仅有一项为1, 其余项均为0时(即5个平面磁梯度传感器中, 当且仅当1个传感器的测量值达到其分辨率), 得到B_XX相对于该非0项对应传感器的分辨率R_i $\begin{matrix} (B_{XX}) \end{matrix}$ ; 由于5个平面磁梯度传感器相对于探头坐标系的方向角φ _i各不相同, 导致B_XX相对于各传感器的分辨率R_i $\begin{matrix} (B_{XX}) \end{matrix}$ 随之不同, 取其中的最大值作为B_XX相对于测量探头的分辨率R_T $\begin{matrix} (B_{XX}) \end{matrix}$ , 表示为:

$\begin{matrix} \{\begin{matrix} R_{i} (B_{XX}) = \frac{\partial B_{XX}}{\partial G_{i}}, i = 1, 2, 3, 4, 5 \\ R_{T} (B_{XX}) = \max (R_{i} (B_{XX})) \end{matrix} (10) \end{matrix}$

式(10)中, 由于构建探头的各平面磁梯度传感器一致性较高, 通过微调平面磁梯度传感器的读出电路增益, 可使各梯度传感器的分辨率R_i相等。令该值为单位1, 得到B_XX的相对于探头的相对分辨率R_r $\begin{matrix} (B_{XX}) \end{matrix}$ (以下简称B_XX的相对分辨率)为:

$\begin{matrix} \begin{matrix} R_{r} (B_{XX}) = \frac{R_{T} (B_{XX})}{R_{i}} = \\ \max (\frac{\partial B_{XX}}{\partial G_{1}}, \frac{\partial B_{XX}}{\partial G_{2}}, \dots, \frac{\partial B_{XX}}{\partial G_{5}}) (11) \end{matrix} \end{matrix}$

同理, 其余独立分量的相对分辨率为:

$\begin{matrix} \{\begin{matrix} R_{r} (B_{YY}) = \max (\frac{\partial B_{YY}}{\partial G_{1}}, \frac{\partial B_{YY}}{\partial G_{2}}, \dots, \frac{\partial B_{YY}}{\partial G_{5}}) \\ R_{r} (B_{XY}) = \max (\frac{\partial B_{XY}}{\partial G_{1}}, \frac{\partial B_{XY}}{\partial G_{2}}, \dots, \frac{\partial B_{XY}}{\partial G_{5}}) \\ R_{r} (B_{XZ}) = \max (\frac{\partial B_{XZ}}{\partial G_{1}}, \frac{\partial B_{XZ}}{\partial G_{2}}, \dots, \frac{\partial B_{XZ}}{\partial G_{5}}) \\ R_{r} (B_{YZ}) = \max (\frac{\partial B_{YZ}}{\partial G_{1}}, \frac{\partial B_{YZ}}{\partial G_{2}}, \dots, \frac{\partial B_{YZ}}{\partial G_{5}}) \end{matrix} (12) \end{matrix}$

由式(11)(12)可知, 5个独立分量相对分辨率的唯一决定因素为各平面磁梯度传感器在探头上的角度参数。由各传感器在探头上的布置方式可知, 该决定因素又可简化为棱台侧面的倾斜角度θ 。

2.2 磁梯度张量5个独立分量相对分辨率

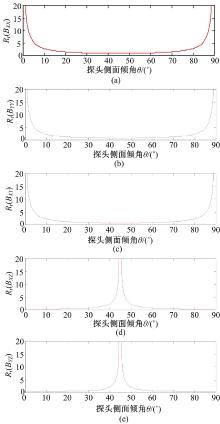
图4为各独立分量的相对分辨率与探头侧面倾角的仿真曲线图, 图中横坐标为探头侧面倾角θ , 纵坐标为各独立分量的相对分辨率。

	Figure Option View Download New Window
	图4 各相对分辨率与倾角θ 的关系图Fig.4 Relation curve of each relative resolution and inclination θ

由图4可知:

(1)当侧面倾角θ =0° 时, 拾取环在B_XX、B_YY、B_XY与B_YX方向上的投影面积为零, 基线在B_ZZ方向上的投影长度为零, 平面磁梯度传感器的测量值中不包含上述5个分量的“ 成分” , 测量系统无法测得上述分量, 即R_r $\begin{matrix} (B_{XX}) \end{matrix}$ 、R_r $\begin{matrix} (B_{YY}) \end{matrix}$ 与R_r $\begin{matrix} (B_{XY}) \end{matrix}$ 为∞ ; 与此同时, B_ZX与B_ZY方向上的拾取环投影面积与基线投影长度均达最大值, 两个分量的分辨率最高, 故R_r $\begin{matrix} (B_{XZ}) \end{matrix}$ 与R_r $\begin{matrix} (B_{YZ}) \end{matrix}$ 取得最小值。

(2)θ =45° 时, 传感器在B_XX、B_YY、B_XY、B_YX与B_ZZ方向上的拾取环投影面积与基线投影长度的乘积均为最大值, 所以R_r $\begin{matrix} (B_{XX}) \end{matrix}$ 、R_r $\begin{matrix} (B_{YY}) \end{matrix}$ 与R_r $\begin{matrix} (B_{XY}) \end{matrix}$ 取得最小值; 与此同时, 平面磁梯度传感器中B_XZ与B_ZX相抵消, 导致测量值中不包含B_XZ与B_ZX的“ 成分” , 故R_r $\begin{matrix} (B_{XZ}) \end{matrix}$ 为∞ , 同理R_r $\begin{matrix} (B_{YZ}) \end{matrix}$ 为∞ 。

(3)θ =90° 时, 传感器基线在B_XX、B_YY、B_XY与B_YX方向上的投影长度为零, 拾取环在B_ZZ方向上的投影面积为零, 平面磁梯度传感器的测量值中不包含B_XX、B_YY、B_XY与B_YX的“ 成分” , 即R_r $\begin{matrix} (B_{XX}) \end{matrix}$ 、R_r $\begin{matrix} (B_{YY}) \end{matrix}$ 与R_r $\begin{matrix} (B_{XY}) \end{matrix}$ 为∞ ; B_XZ与B_YZ方向上的拾取环投影面积与基线投影长度均达最大值, 即R_r $\begin{matrix} (B_{XZ}) \end{matrix}$ 与R_r $\begin{matrix} (B_{YZ}) \end{matrix}$ 取得最小值。

(4)由于B_XY=B_YX, B_XZ=B_ZX, B_YZ=B_ZY, 5个独立分量的相对分辨率相对于探头侧面倾角的变化曲线以θ =45° 轴对称。

5个独立分量的相对分辨率相对于探头侧面倾角的取值及变化趋势截然不同。在进行磁梯度张量反演时, 5个独立分量分辨率的不一致, 必然导致待测目标体的定位及成像产生失真; 同时, 反演质量也受制于5个独立分量相对分辨率中的最大值。因此, 可通过评估不同角度下的5个独立分量相对分辨率的离散度与最大值优化探头的侧面倾角。

2.3 五棱台式探头侧面最优倾斜角度

2.3.1 离散度

从磁梯度张量分辨率的角度分析, 各独立分量的分辨率决定磁梯度张量不变量等反演结果的分辨率^[1], 5个相对分辨率的离散导致反演结果在三维空间各方向上的分辨率不一致, 从而造成目标体定位与成像失真, 个别数据偏离均值的程度越大, 失真越严重。

常用的离散度评估标准有标准差、平均差与极差。其中, 标准差与平均差用于衡量一组数据的平均偏离程度, 对数据的最大偏移量有抑制作用(即一组数据中多数数据高度集中, 个别数据严重偏离均值, 但数据的标准差与均差有可能很小); 极差用于衡量一组数据的极限离散程度, 对最大偏移量敏感。因此, 本文采用极差Range作为离散度评估标准, 表示为:

$\begin{matrix} \{\begin{matrix} Range = \max (R_{r}) - \min (R_{r}) \\ R_{r} = {R_{r} (B_{XX}), R_{r} (B_{YY}), R_{r} (B_{XY}), \\ R_{r} (B_{XZ}), R_{r} (B_{YZ})} \end{matrix} \end{matrix}$ (13)

式中:R_r为5个独立分量相对分辨率的集合; max(R_r)为R_r中的最大值; min(R_r)为R_r中的最小值。

图5为5个独立分量相对分辨率的极差相对于侧面倾角的仿真曲线。由图5可知, 当θ 为56.6° 或33.4° 时, 5个独立分量相对分辨率的极差均取最小值。此时, 探头测得的磁梯度张量数据反演时, 目标体定位与成像的失真最小。

	Figure Option View Download New Window
	图5 极差与倾角θ 的关系图Fig.5 Relation curve of range and inclination θ

2.3.2 最差相对分辨率

分析磁梯度张量相对分辨率的极差可得到磁梯度张量反演失真度最小时的探头侧面倾角。但是, 失真度最小并不代表系统的整体分辨率最高, 磁梯度张量测量系统的整体分辨率受制于5个独立分量的最差分辨率。为此, 补充评估相对分辨率的第二个标准— — 最差相对分辨率(5个独立分量相对分辨率的最大值max(R_r))。

图6为5个独立分量最差相对分辨率相对于侧面倾角的仿真曲线。由图可知, 当θ 为56.6° 或33.4° 时, 5个独立分量最差相对分辨率取得最小值, 略大于平面磁梯度传感器的分辨率。此时, 探头测得的磁梯度张量数据反演时, 目标体定位与成像的分辨率最高。

	Figure Option View Download New Window
	图6 最差相对分辨率与倾角θ 的关系图Fig.6 Relation curve of worst relative resolution and inclination θ

2.3.3 五棱台式探头最优侧面倾角分析

从5个独立分量相对分辨率的极差和最差分辨率的角度考虑, 五棱台式探头的倾角优化值均为56.6° 和33.4° , 与Eschner等^[6]给出的基于最小标准差的优化值(58° 或32° )略有差别。

表1列出了上述两种优化倾角下5个独立分量的相对分辨率及最大偏移量相对于均值与中位数的偏移值。可以看出:当倾角为58° 时, 最大偏移量(R_r $\begin{matrix} (B_{XX}) \end{matrix}$ )相对于五个相对分辨率的均值与中位数的偏移均大于倾角为56.6° 时的取值(倾角为56.6° 时最大偏移量为R_r $\begin{matrix} (B_{XY}) \end{matrix}$ ), 即标准差对R_r $\begin{matrix} (B_{XX}) \end{matrix}$ 的偏离进行了抑制, 无法衡量5个相对分辨率的最大偏移量(对应反演结果的最大失真); 此外, 当倾角为56.6° 时, 5个相对分辨率中的最差相对分辨率取最小值, 反演结果的整体分辨率最高。因此, 侧面倾角为56.6° (或33.4° )比58° (或32° )更合理。

表1 侧面倾角为56.6° 或58° 时5个相对分辨率的最大偏移量相对于均值与中位数的偏移值 Table 1 Offset of the largest offset of five relative resolutions relatives to the mean and median when inclination is 56.6° or 58°

由于侧面倾角为33.4° 时探头的底面积过大, 考虑到杜瓦直径对探头底面积的限制, 探头的最优倾角定为56.6° 。

3 加工误差分析

由于加工工艺的限制, 探头的侧面倾角存在着一定的加工误差, 对探头的测量结果造成一定的影响。为此, 定量分析了由探头倾角误差造成的各独立分量的相对误差, 见图7。

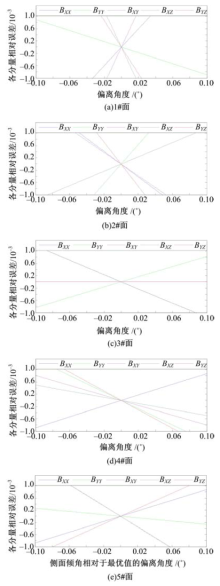	Figure Option View Download New Window
	图7 各独立分量相对误差相对于五个倾角误差的变化曲线Fig.7 Relation curve of each component’ relative error and sensitive sloping surface’ tilt error

探头加工过程中, 5个侧面倾角的加工误差各不相同。为了研究方便, 本文假设5个侧面中的1个侧面存在倾角误差, 图7为5个独立分量相对误差随倾角误差的变化曲线。

由图7可知, 各独立分量的相对误差与五棱台各侧面的倾角误差近似成比例关系; 通过将两者间的比例系数进行对比可知, 同一侧面的倾角误差对5个独立分量相对误差的影响各不相同, 且5个侧面对同一分量相对误差的影响也不相同。表2列出了对各独立分量相对误差影响最大的倾角误差的所属侧面(表中称为敏感面), 以及各独立分量相对误差与敏感面倾角误差的比值(表中称为比值)。

表2 各分量相对误差与敏感面倾角误差的比值 Table 2 Ratio of each component’ s relative error and sensitive sloping surface’ tilt error

目前, 常规的机械加工工艺可将探头侧面倾角的精度控制在0.01° 左右, 用于精密加工的五轴联动数控机床可将精度提高到0.001° 。根据具体的应用环境、测量目标以及所采用传感器的分辨率, 可以参考表2列出的比值选择合适的探头加工工艺。

4 结束语

针对基于平面超导磁梯度传感器的五棱台式全张量磁梯度测量探头, 提出了一种探头侧面倾角的优化方法。通过量化分析磁梯度张量5个独立分量的相对分辨率, 并以5个独立分量相对分辨率的极差与最大值为依据, 得出探头侧面的最优倾角为56.6° 。最后, 通过仿真得了各分量相对误差与敏感面侧面倾角误差的比例系数, 为棱台的加工工艺明确了精度要求。上述方法也适用于其他形状的基于平面超导磁梯度传感器的棱台式探头的侧面倾角优化。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Schmidt P W, Clark D A. The magnetic gradient tensor: its properties and uses in source characterization[J]. The Leading Edge, 2006, 25(1): 75-78. [本文引用:2]
[2]	Keenan S T, Young J A, Foley C P, et al. A high-T_c flip-chip SQUID gradiometer for mobile underwater magnetic sensing[J]. Superconductor Science and Technology, 2010, 23(2): 025029. [本文引用:1]
[3]	张光, 张英堂, 尹刚, 等. 基于线性误差模型的磁张量系统校正[J]. 吉林大学学报: 工学版, 2015, 45(3): 1012-1016. Zhang Guang, Zhang Ying-tang, Yin Gang, et al. Calibration method of magnetic tensor system based on linear error model[J]. Journal of Jilin University(Engineering and Technology Edition), 2015, 45(3): 1012-1016. [本文引用:1]
[4]	Gamey T J, Doll W E, Beard L P, et al. Design and testing an airborne SQUID magnetometer for UXO detection[J]. SAGEEP, 2005, 18(1): 718-735. [本文引用:1]
[5]	Bick M, Leslie K E, Binks R A, et al. Axial high-temperature superconducting gradiometer with a flexible flux transformer[J]. Applied Physics Letters, 2004, 84(26): 5347-5349. [本文引用:1]
[6]	Eschner W, Ludwig W. Planar gradiometers arranged on non-parallel surfaces for determination of a gradient tensor of a magnetic field[P]. US: 5469056, 1995 [本文引用:2]
[7]	申茂冬, 安战锋, 程德福, 等. 航空超导全张量磁梯度测量系统相关参数获取装置及方法[P]. 中国: 201410634524. 6, 2014-11-07. [本文引用:3]
[8]	伍俊, 荣亮亮, 邱隆清, 等. 一种基于GPS同步的航空超导全张量磁梯度测控装置[P]. 中国: 201410742613. 2, 2014-12-08. [本文引用:1]
[9]	低温超导磁梯度张量系统JESSY STAR[EB/OL]. [2013-04-02]. http://www.supracon.com/en/star.html. [本文引用:1]
[10]	张昌达. 航空磁力梯度张量测量——航空磁测技术的最新进展[J]. 工程地球物理学报, 2006, 3(5): 354-361. Zhang Chang-da. Airborne tensor magnetic grand iometry—the latest progress of airborne magnetometric technology[J]. Chinese Journal of Engineering Geophysics, 2006, 3(5): 354-361. [本文引用:1]
[11]	Cantor R, Hall J A, Matlachov A N, et al. First-order planar superconducting quantum interference device gradiometers with long baseline[J]. IEEE Transactions on Applied Superconductivity, 2007, 17(2): 672-675. [本文引用:1]

2006

0.0

... 航空全张量磁梯度测量是最新一代的航磁测量技术,由于其测量对象受地磁场的倾角、偏角影响小,由磁梯度张量计算得到的张量不变量不需额外处理即可很好地描述磁场源,磁梯度张量反演能够高质量地描述场源体的磁化方向和几何形态(如倾向、走向等),提高了对磁源体的分辨率,因此,在航磁测量中具有不可比拟的优势,成为国内外航空磁法勘探与军事探潜等领域的一个研究热点^[1,2] ...

... 从磁梯度张量分辨率的角度分析,各独立分量的分辨率决定磁梯度张量不变量等反演结果的分辨率^[1],5个相对分辨率的离散导致反演结果在三维空间各方向上的分辨率不一致,从而造成目标体定位与成像失真,个别数据偏离均值的程度越大,失真越严重 ...

2010

0.0

2015

0.0

. 2015, 45(3):1012-1016 DOI:doi:10.13229/j.cnki.jdxbgxb201503048

Calibration method of magnetic tensor system based on linear error model

基于线性误差模型的磁张量系统校正

Zhang Guang , Zhang Ying-tang , Yin Gang

张光, 张英堂, 尹刚

摘　要：针对磁张量系统中存在单个三轴磁场传感器自身误差（三轴非正交性误差、各轴灵敏度不一致误差和零点偏移误差等）和三轴磁场传感器轴系间对正误差的问题，提出基于线性模型的磁张量系统校正方法。对于单个三轴磁场传感器建立了关于三轴非正交、各轴灵敏度不一致和零点偏移的线性误差模型，对于三轴磁场传感器轴系间对正误差建立了关于坐标系旋转角度的线性误差模型，通过广义逆的方法求解得到误差参数，将求解得到的误差参数代入测量数据，实现对磁张量系统的校正。实际测量试验表明，本文所提方法可以有效减小单个三轴磁场传感器自身误差和三轴磁场传感器轴系间的对正误差。

... 可构成全张量磁梯度测量系统的磁传感器主要有磁通门与基于超导量子干涉器(Supercon-ducting quantum interference devices,SQUID)的磁强计、轴向磁梯度传感器和平面磁梯度传感器^[3,4,5,6] ...

2005

0.0

2004

0.0

1995

0.0

... ,与Eschner等^[6]给出的基于最小标准差的优化值(58#cod#x000b0 ...

0.0

... 因此,多个国家正在积极研制基于平面超导磁梯度传感器的航空超导全张量磁梯度测量系统,德国耶拿物理高技术研究所已研制出全球唯一一套实用化的全张量磁梯度测量系统^[7,8,9] ...

... 超导全张量磁梯度测量系统中,利用5个平面超导磁梯度传感器构建成五棱台式张量测量探头^[7] ...

... 将5个平面超导磁梯度传感器搭建成正五棱台结构的张量探头^[7],利用5个平面磁梯度传感器的测量值可求得磁梯度张量的5个独立分量 ...

0.0

2013

0.0

2006

0.0

... 1 磁梯度张量图1为磁梯度张量分量解析图,由图可知,磁场强度 B→的3个分量(B_X B_Y B_Z)在空间中3个方向(X Y Z)上的变化率构成磁梯度张量T^[10],表示为: ...

2007

0.0

... 2 平面超导磁梯度传感器图2为平面超导磁梯度传感器结构示意图,该传感器主要由SQUID磁强计、耦合线圈及拾取环等部件组成^[11] ...