变速器斜齿轮宏观参数减振优化设计

引用本文

宗长富, 任明辉, 万滢, 陈涛, 白鹰搏. 变速器斜齿轮宏观参数减振优化设计. 吉林大学学报:工学版, 2016, 46(6): 1772-1779
ZONG Chang-fu, REN Ming-hui, WAN Ying, CHEN Tao, BAI Ying-bo. Optimization of macro-geometric parameters of helical gears of transmissions to reduce vibration. Journal of Jilin University Engineering and Technology Edition, 2016, 46(6): 1772-1779 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201606003
Permissions

变速器斜齿轮宏观参数减振优化设计

宗长富¹, 任明辉^1,², 万滢¹, 陈涛², 白鹰搏³

1.吉林大学汽车仿真与控制国家重点实验室,长春 130022

2.中国第一汽车股份有限公司技术中心,长春 130062

3.吉林大学机械科学与工程学院,长春 130022

作者简介:宗长富(1962-),男,教授,博士生导师.研究方向:汽车参数匹配、仿真与控制.

基金项目:国家自然科学基金项目(51575224,51575223); 吉林省科技发展计划项目(20150204066GX)

摘要

为了在变速器齿轮宏观参数设计阶段尽可能地降低齿轮啮合冲击振动,提出了一种斜齿轮宏观参数的减振优化设计方法。采用减小传递误差波动值作为减小冲击振动的手段,建立以减小冲击振动和体积为目标,同时考虑规范要求并保证强度的变速器斜齿轮宏观参数优化模型,采用遗传算法进行寻优。斜齿轮传递误差的计算方法考虑将斜齿轮副近似为众多小直齿轮副的叠加,并考虑相邻小直齿轮副的啮合角度的相位差,小直齿轮副的传递误差计算采用考虑轮体周向变形的改进石川法。优化结果表明,本文优化方法能够有效降低斜齿轮传递误差41%、降低体积1.34%。

关键词: 车辆工程; 变速器; 斜齿轮; 传递误差; 减振优化; 宏观参数

中图分类号:U463.212 文献标志码:A 文章编号:1671-5497(2016)06-1772-08

Optimization of macro-geometric parameters of helical gears of transmissions to reduce vibration

ZONG Chang-fu¹, REN Ming-hui^1,², WAN Ying¹, CHEN Tao², BAI Ying-bo³

1.State Key Laboratory of Automotive Simulation and Control,Jilin University,Changchun 130022,China

2.R&D Center, China FAW Group Corporation, Changchun 130062,China

3.College of Mechanical Science and Engineering, Jilin University, Changchun 130022,China

Abstract

A method to optimize the macro-parameters of helical gears in transmissions is developed to reduce meshing vibration in initial design phase of the transmission gearbox. In the optimization model, the optimization variables include the modulus, the helical angle, the tooth wide, the top gap coefficient etc. The optimization target is the synthesis of reducing meshing vibration and reducing the volume of the gear pair. The constraint conditions include the standard requirements and the strength requirement. The fluctuation value of the dynamic transmission error is considered as the index of the vibration. To calculate the dynamic transmission error of the helical gear pairs, the helical gear pair is approximated as the superposition of many smaller spur gear pairs, and the phase difference of the meshing angles of adjacent smaller spur gear pairs is considered. The deformation calculated by Ishikawa method and the circumferential deformation are considered in the dynamic transmission error and the dynamic meshing stiffness calculation of the smaller spur gear pairs. The optimization results show that the method developed in this paper can effectively reduce the transmission error of the helical gear by 41% and reduce the volume by 1.34%.

Key words: vehicle engineering; transmission; helical gears; transmission error; vibration damping optimization; macro-geometric parameters

Show Figures

0 引言

变速器齿轮振动和噪声的影响因素包括齿轮的设计和加工、齿轮轴承和齿轮箱的结构设计等。至今大多研究工作都集中在理论和试验研究、数值仿真等阶段。在箱体整体噪声方面, 李宏坤等^[1]在对某齿轮箱进行模态贡献量和面板声学贡献量分析的基础上, 将主要固有频率和面板声功率级作为目标函数, 应用有限元软件进行了箱体厚度的减振优化设计。关于齿轮副的设计方面, 当齿轮的类型、材料都确定后, 影响振动和噪声的指标包括齿轮几何宏观参数、微观修形方式和修形量两个方面^[2]。微观修形对齿轮的啮入、啮出冲击激励有很大影响, 是目前对齿轮振动和噪声优化设计的主要手段^{[3, 4, 5]}。齿轮的几何宏观参数(包括齿数、模数、螺旋角、重合度等)是影响齿轮时变啮合刚度激励波动的根源。在宏观参数设计阶段, 基本是通过经验和定性分析来确定和调整齿轮几何宏观参数, 使得齿轮的噪声品质满足要求, 或是单纯地通过提高重合度来优化齿轮振动和噪声品质^{[6, 7]}。

齿轮动力学研究^[8]表明, 齿轮箱系统的振动很大程度上取决于各齿轮副的动态传递误差。动态传递误差波动越大, 越不利于传动的振动抑制。齿轮啮合过程中的受载弹性变形是动态传递误差的一个分量, 称为设计传递误差, 与决定于齿轮宏观几何参数的齿轮动态啮合刚度直接相关。因此, 如果能通过对齿轮宏观几何参数的优化设计, 减小动态传递误差中弹性变形部分的波动量, 就能在齿轮宏观参数设计阶段更好地考虑对噪声的要求, 从而提升齿轮的振动和噪声性能。

在设计变速器时, 一般通过MASTA等变速器设计专用软件或ANSYS等有限元软件计算齿轮的传递误差, 但MASTA软件不能对传递误差进行优化设计, 需要手动修改参数反复尝试, 而有限元软件建模复杂且计算时间长^[9]。由于齿轮系统非线性动力学微分方程的求解必须依靠高精度数值解, 因此有很多研究对摄动法等近似解析法进行了研究。李瑰贤等^[10]提出采用多尺度法近似求解齿轮系非线性微分方程。传统石川法或改进石川法是一种基于材料力学理论的快速计算直齿轮时变啮合刚度和设计传递误差的较好方法^[11], 但该方法只适用于直齿轮。Wei等^[12]建立了六自由度斜齿轮啮合动力学模型, 用于计算齿轮啮合的传递误差, 并用该模型分析了齿轮重合度、轴支撑刚度、啮合阻尼等齿轮参数对动态传递误差的影响。Kang等^[13]采用有限元方法建立了斜齿轮的传递误差计算模型, 并用该模型计算不同螺旋角下的齿轮重合度和传递误差, 建立了重合度、传递误差与螺旋角之间的关系。对于其他齿轮形式, 刘志峰等^[14]针对等高齿锥齿轮提出将时变啮合刚度表示为啮合中心沿齿面法向位移的多项式函数。此外, 也有少数研究建立了齿轮传动系整体动力学模型, 如符升平等^[15]建立了多级齿轮传动刚柔耦合动力学模型, 综合考虑了传动轴各向柔性、湿式离合器动特性及齿轮时变啮合力对轴类零件动态响应的影响。

综上可知, 目前的研究中主要存在两点不足:①忽略了齿轮宏观几何参数设计阶段对噪声和振动的设计要求, 或仅进行相关性和趋势的分析; ②斜齿轮传递误差计算大多采用有限元方法, 由于计算速度慢导致不易实现优化设计。为此, 本文针对变速器普遍采用的斜齿轮, 提出了一种快速运行的变速器斜齿轮宏观参数优化设计方法, 通过减小齿轮啮合的传递误差减小冲击振动。首先建立以斜齿轮的齿数、模数、螺旋角、齿宽、顶隙系数等为变量的传递误差计算模型, 将斜齿轮副近似看作很多具有相同端面参数的小直齿轮副的叠加, 并考虑相邻小直齿轮副啮合时间和啮合角度的相位差, 对每个小直齿轮副采用石川法计算动态啮合刚度和传递误差, 通过对所有小直齿轮副啮合刚度进行叠加, 建立斜齿轮的动态啮合刚度模型和相应传递误差计算模型。然后采用减小传递误差波动值作为减振的手段, 建立以减小振动和体积为目标, 同时保证强度和使用过程中的可靠性的变速器斜齿轮宏观参数的优化设计模型, 并采用遗传算法对变速器斜齿轮进行优化设计。

1 斜齿轮传递误差计算模型

齿轮啮合的传递误差由受载轮齿的弹性形变和齿轮的制造误差两部分组成。在设计过程中, 不考虑制造误差, 因此本文仅考虑理想齿轮状态下由轮齿受载弹性形变引起的传递误差。斜齿轮的原始参数如下:法面模数m_n=3.7; 螺旋角β =24° ; 有效齿宽b=29 mm; 实际中心距a_w=135 mm; 弹性模量E=207 000 MPa; 泊松比 v=0.3, 其他参数见表1。此外, 该斜齿轮副受到的啮合转矩为126.2 N· m, 主动轮转速为1400 r/min。

表1 斜齿轮原始参数 Table 1 Original parameters of helical gears

参数	数值
参数	主动轮	从动轮
齿数z	37	30
法面压力角α _n/(° )	20	20
法向齿顶高系数 $\begin{matrix} h_{a}^{*} \end{matrix}$	1.4	1.4
法向顶隙系数c^*	1.7	1.7
变位系数x_n	-0.5868	-0.1222

表1 斜齿轮原始参数 Table 1 Original parameters of helical gears

1.1 端面直齿轮副的综合啮合动刚度计算

端面直齿轮副是指与斜齿轮具有相同端面参数、齿宽相同的端面直齿轮副。首先计算端面直齿轮上单个轮齿的变形 δ _j, 考虑传统石川法计算的变形量和轮体周向变形量。

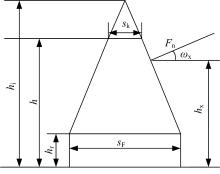
	Figure Option View Download New Window
	图1 石川法结构示意图Fig.1 Structure schematic of Ishikawa method

采用石川法计算直齿轮啮合变形时, 将齿轮看成是长方形和梯形的组合, 考虑在载荷作用下长方形和梯形的弯曲和剪切变形。图1为石川法计算直齿轮啮合变形的几何示意图, 其中h_r、s_F分别为矩形的高和宽; h为矩形和梯形总高; h_i为梯形腰长延伸后得到的三角形的高; s_k为梯形上边长; ω _x、h_x分别为载荷F_n作用方向和作用点至矩形底边的高度。根据石川法计算的变形量δ _石为:

$\begin{matrix} δ_{石} = δ_{Br} + δ_{Bt} + δ_{s} + δ_{G} \end{matrix}$ (1)

式中:δ _Br、δ _Bt、δ _s和δ _G分别为长方形部分弯曲变形量、梯形部分的弯曲变量、剪力产生的变形量和基础部分倾斜产生的变形量。

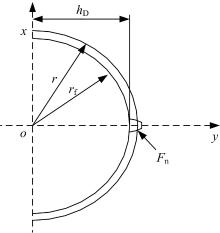
直齿轮的轮体周向变形δ _ω计算原理是将齿轮圆心的水平轴至轮齿危险截面间的齿轮复板简化为一个曲边梯形, 如图2所示。切向力F_ncosω _x导致的腹板剪切变形和弯曲变形之和即为所考虑的轮体周向变形(包括切向变形和弯曲变形)为:

$\begin{matrix} δ_{ω} = δ_{ω 1} + δ_{ω 2} \end{matrix}$ (2)

腹板剪切变形δ _{ω 1}和腹板弯曲变形δ _{ω 2}分别为:

$\begin{matrix} \begin{matrix} δ_{ω 1} = \iint \frac{- 3 F_{n} \cos ω_{x} (\sqrt[]{r_{f}^{2} - y^{2}} - y)}{2 Eb (r_{f}^{2} - y^{2})^{\frac{3}{2}}} d y^{2} (3) \\ δ_{ω 2} = \iint \frac{- 3 F_{n} \cos ω_{x} h_{x}}{2 Eb (r_{f}^{2} - y^{2})^{\frac{3}{2}}} d y^{2} (4) \end{matrix} \end{matrix}$

	Figure Option View Download New Window
	图2 轮体周向变形几何示意图Fig.2 Geometric schematic of wheel circumferential deformation

综合石川法和轮体周向变形的计算, 端面直齿轮上单个轮齿沿啮合线方向的变形量δ _j为:

$\begin{matrix} δ_{j} = (δ_{石} + δ_{ω})_{j} = (δ_{Br} + δ_{Bt} + δ_{s} + δ_{G} + δ_{ω})_{j} \end{matrix}$ (5)

式中:j={1, 2}, 1表示主动轮, 2表示从动轮。

端面直齿轮副的单对轮齿的啮合动刚度k_s为:

$\begin{matrix} k_{s} = \frac{F_{n}}{δ_{s}} \end{matrix}$ (6)

式中:F_n为一对轮齿啮合的相互作用力, 与单个轮齿受到的作用力一样; δ _s=δ ₁+δ ₂, 包括主动轮和从动轮两个齿轮的变形。

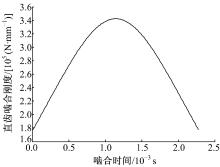
计算得到斜齿轮参数对应的端面直齿轮的单对轮齿啮合刚度随啮合时间变化曲线如图3所示。

	Figure Option View Download New Window
	图3 端面直齿轮单对轮齿时变啮合刚度Fig.3 Meshing stiffness of a pair of teeth of spur gear pair

通常齿轮在啮合期间有多对轮齿同时参与啮合, 因此整个端面直齿轮副的时变啮合刚度是多对轮齿啮合刚度的合成。计算斜齿轮的端面重合度为:

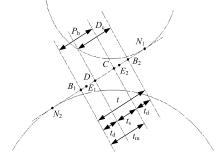
$\begin{matrix} ε_{α} = [z_{1} (\tan α_{α 1} - tanα') + z_{2} (\tan α_{α 2} - tanα')] / (2 π) = 1.9676 \end{matrix}$ (7)

ε _α在1~2之间, 即端面直齿轮副在啮合过程中存在一对轮齿啮合和两对轮齿同时啮合两种情况, 对直齿轮副一对轮齿的啮合周期进行划分(见图4), 其中, B₁B₂为实际啮合线段; P_b为一个基节的长度; B₁D和CB₂为双齿啮合区; DC为单齿啮合区; t_m为一对轮齿的啮合周期(即齿轮副走过一个基节的时间); t_d为双齿啮合区DCP; t_s为单齿啮合区SCP。一对轮齿从接触啮合到完全分离的时间为2t_d+t_s。设定主动轮的转速为n_z, 则转过一个基节的时间为t_m=60/(z₁n₂)。设λ =t_d/t_m, 则与端面重合度ε _α的关系为:λ =ε _α-1。

	Figure Option View Download New Window
	图4 端面直齿轮副的啮合过程示意图Fig.4 Meshing process of transverse spur gear pair

设E₁、E₂分别是位于B₁D段和CB₂段的两对轮齿对的同时啮合点。双齿啮合时, 齿轮副的综合啮合刚度是这两个轮齿对的啮合刚度之和(相当于并联弹簧), 则双齿啮合时端面直齿轮副的综合啮合刚度为:

$\begin{matrix} K_{d} = k_{s} (E_{1}) + k_{s} (E_{2}) \end{matrix}$ (8)

一个啮合周期t_m内, 端面直齿轮副的综合时变啮合刚度K_m直可表示为:

$\begin{matrix} K_{m 直} = \{\begin{matrix} K_{d}, 0 \leq t \leq t_{d} \\ K_{s}, t_{d} < t \leq t_{m} \end{matrix} \end{matrix}$ (9)

若重合度为2~3, 则有:

$\begin{matrix} K_{m 直} = \{\begin{matrix} K_{t}, 0 \leq t \leq t_{t} \\ K_{d}, t_{t} < t \leq t_{d} \end{matrix} (10) \end{matrix}$

式中:K_t、K_d分别为三齿啮合和双齿啮合的综合刚度; t_t、t_d分别为三齿啮合区和双齿啮合区。

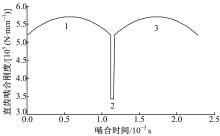
端面直齿轮副的综合啮合刚度随时间的变化如图5所示。从图可以看出:1、3段互为平移函数。由于是离散化计算, 因此结果是离散的。为便于之后计算斜齿轮副的综合时变啮合刚度, 对图中1、2段曲线进行三次多项式拟合, 得到第1段和第2段的拟合函数分别为:

$K_{m 直 1} (t) = o_{11} t^{3} + o_{12} t^{2} + o_{13} t + o_{14} 0 \leq t \leq t_{d} (11)$

$\begin{matrix} K_{m 直 2} (t) = o_{21} t^{3} + o_{22} t^{2} + o_{23} t + o_{24} t_{d} < t \leq t_{m} \end{matrix}$ (12)

	Figure Option View Download New Window
	图5 端面直齿轮副的综合时变啮合刚度Fig.5 Dynamical meshing stiffness of spur gear pair

1.2 斜齿轮副的动态传递误差计算

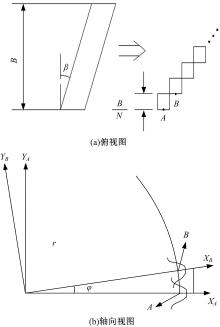直齿轮的齿廓曲面是发生面在基圆柱上做纯滚动时, 发生面上一条与齿轮轴相平行的直线KK所展成的渐开线曲面, 斜齿圆柱齿轮齿廓曲面的形成原理与直齿圆柱齿轮相似, 但是发生面上的直线KK不平行于基圆柱的轴线, 而是与其有一个螺旋角β 。所以在模型上, 如图6(a)所示, 把宽度为B、螺旋角为β 的斜齿轮近似看作是N个具有相同端面参数小直齿轮副的叠加, 每个小直齿轮的宽度为B/N。从啮合的角度来看, 如图6(b)所示, 图中每对小直齿轮副(以i+1表示)比前一对小直齿轮副(以i表示)超前角度φ 。A、B在图6(b)所示平面的投影弧长为 $\begin{matrix} \overset{⌢}{AB} \end{matrix}$ , 则超前角度φ 的计算公式为:

	Figure Option View Download New Window
	图6 斜齿轮等效为小直齿轮的俯视图和轴向视图Fig.6 Equivalence of helical gears and set of narrow spur gears-vertical view and axial view

$\begin{matrix} φ = \frac{\overset{⌢}{AB}}{r} = \frac{Btanβ}{Nr} (13) \end{matrix}$

式中: $\begin{matrix} \overset{⌢}{AB} \end{matrix}$ 为两个相邻小直齿轮的端面分度圆弧长; r为端面分度圆半径。

从啮合的时间相位差来考虑, 首、尾小直齿轮副的时间相位差为:

$\begin{matrix} ΔT = \frac{Btanβ}{r} \frac{Tz}{2 π} \end{matrix}$ (14)

相邻小直齿轮副i和i+1的时间相位为:

$\begin{matrix} Δ T_{i} = \frac{ΔT}{N} = \frac{Btanβ}{Nr} \frac{Tz}{2 π} \end{matrix}$ (15)

式中:T为斜齿轮副的啮合周期, 也是转过一个齿所需要的时间。

根据前面计算得到的端面直齿轮副整体啮合动刚度K_m直可得宽度为B/N的第i个小直齿轮副的综合时变啮合刚度为:

$\begin{matrix} k_{i} (t) = \frac{1}{N} K_{m 直} (t - \frac{i - 1}{N} \frac{Btanβ}{r} \frac{Tz}{2 π}) \end{matrix}$ (16)

对N取极限并求所有小直齿轮副刚度之和, 得到斜齿轮副的整体啮合刚度K_斜(t)为:

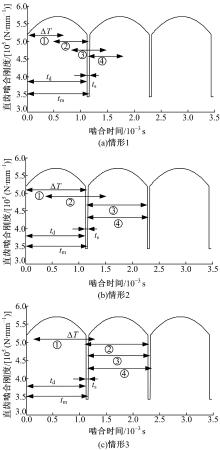
$\begin{matrix} K_{斜} (t) = \lim_{N \to \infty} \overset{N - 1}{\underset{i = 0}{\sum k_{i} (t)}} = \lim_{N \to \infty} [\frac{1}{N} \overset{N - 1}{\underset{i = 0}{\sum K_{直}}} (t - \frac{iΔT}{N})] = \frac{1}{ΔT} \int_{t-ΔT}^{t} K_{直} (t) dt \end{matrix}$ (17)

由于K_m直(t)为分段函数, 式(17)根据端面直齿轮副啮合周期t_m与斜齿轮首、尾小直齿轮副的啮合时间相位差Δ T的大小关系分为3种情况:

(1) Δ T≤ t_d, 随着时间的推进会出现的积分区间的组合如图7(a)所示, 包括4种情况:①双齿区; ②双-单区; ③双-单-双区; ④单-双区。

	Figure Option View Download New Window
	图7 斜齿轮副啮合刚度计算Fig.7 Meshing stiffness calculation of hehical gear pair

(2) t_d< Δ T≤ t_m, 随着时间的推进会出现的积分区间的组合如图7(b)所示, 包括4种情况:①双-单区; ②双-单-双区; ③单-双区; ④单-双-单区。

(3) Δ T> t_m, 随着时间的推进会出现的积分区间的组合如图7(c)所示, 包括4种情况:①双-单-双区; ②双-单-双-单区; ③单-双-单区; ④单-双-单-双区。

1、2段小直齿轮啮合刚度可通过式(11)(12)计算得到, 3~6段可通过1、2段函数平移得到。得到K_斜(t)后, 动态传递误差e_T(t)及传递误差最大波动值Δ e_T0为:

$\begin{matrix} \begin{matrix} e_{T} (t) = \frac{F_{N}}{K_{斜} (t)} (18) \\ Δ e_{T 0} = \max e_{T} (t) - \min e_{T} (t) (19) \end{matrix} \end{matrix}$

式中:F_N为整个齿轮受到的周向力。

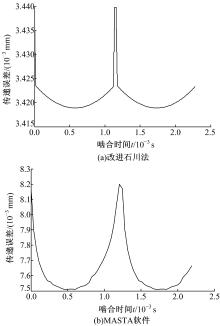
图8(a)(b)分别为本文提出的改进石川法和MASTA软件计算的斜齿轮啮合过程中的动态传递误差, 可以看出其变化趋势一致, 故本文方法可行。

	Figure Option View Download New Window
	图8 斜齿轮啮合动态传递误差Fig.8 Dynamic transmission error of helical gear pair

2 斜齿轮宏观参数减振优化模型

2.1 优化变量和范围

从尽量保证参数间的独立性出发, 本文考虑的斜齿轮主要设计结构参数及其变化范围如下:模数为3.5~5; 压力角为18° ~25° ; 螺旋角为18° ~26° ; 齿宽为6~8.5 mm; 主、从动轮齿顶高系数均为1~2; 主、从动轮顶隙系数均为0.28~0.35。传动比在动力性设计中已经确定, 因此从动轮齿数Z₂=iZ₁。

2.2 优化目标函数

本文的主要优化目标是实现变速器斜齿轮的宏观参数减振设计, 由于齿轮宏观参数与设计传递误差(即齿轮啮合受载弹性变形)直接相关、设计传递误差是动态传递误差的设计分量、动态传递误差的波动量决定了个齿轮副的振动程度, 因此第1个优化目标是尽量降低设计传递误差波动值; 同时, 在保证必要的强度和可靠性的前提下, 应该尽量减少齿轮的体积和质量, 因此第2个优化目标为尽量减少齿轮体积。

目标函数一:

$\begin{matrix} f_{1} (X) = Δ e_{T 0} \end{matrix}$ (20)

目标函数二:

$\begin{matrix} f_{2} (X) = V_{总} = \frac{πb}{4} \frac{m_{n}^{2} (z_{1}^{2} + z_{2}^{2})}{co s^{2} β} \end{matrix}$ (21)

采用线性权重加权法, 将两个优化目标转化为一个, 具体加权方式如下式表示:

$\begin{matrix} f (X) = W_{1} f_{1} (X) + W_{2} f_{2} (X) (22) \end{matrix}$

式中:W₁=1/ $\begin{matrix} f_{1}^{*} \end{matrix}$ (X)为体积加权系数, $\begin{matrix} f_{1}^{*} \end{matrix}$ (X)为体积单目标最优值; W₂=1/ $\begin{matrix} f_{2}^{*} \end{matrix}$ (X)为传递误差波动加权系数, $\begin{matrix} f_{2}^{*} \end{matrix}$ (X)为齿轮动态传递误差波动值单目标最优值。

2.3 约束条件

除了对优化变量的上、下限进行约束, 在斜齿轮的优化中还需要考虑对齿轮的强度、主从动齿轮中心距、轴向力等的要求。

(1)名义中心距约束。受整车和变速箱结构的约束, 名义中心距s₀是确定的, 有如下非线性约束方程成立:

$\begin{matrix} \frac{m_{n} (z_{1} + z_{2})}{2 co s^{2} β} = s_{0} \end{matrix}$ (23)

(2)不发生根切的最小变位系数约束。为保证z< z_min时不发生根切, 需限制变位系数:

$\begin{matrix} x < x_{\min \min} \end{matrix}$ (24)

(3)齿顶齿厚约束。根据齿轮加工要求, 齿顶圆法面弧齿厚满足如下关系:

$\begin{matrix} s_{nt} \geq 0.3 m_{n} \end{matrix}$ (25)

(4)其他噪声指标的约束。总结研究成果和工程实践结果可知:①啮合起始点远离基圆可降低噪声, ②齿轮副啮入段小于啮出段长度可降低噪声。据此确定两个噪声指标约束如下:

$\begin{matrix} \begin{matrix} β_{cg} = \frac{d_{b} + 0.1 t_{n}}{d_{fa}} < 1 (26) \\ β_{z} = \frac{2 ρ_{2 \max} - d_{b 2} \tan α_{s}}{2 ρ_{1 \max} - d_{b 1} \tan α_{s}} < 0.9 (27) \end{matrix} \end{matrix}$

式中:β _cg为控制滑动比; β _z为控制摩擦力突变; d_b为基圆直径; t_n为法向齿距; d_fa为啮合起始圆直径; ρ _1max、ρ _2max分别为主、从动齿轮最大曲率半径; d_b1、d_b2分别为主、从动齿轮基圆直径; α _s为端面啮合角。

(5)强度约束。齿轮最重要的两种失效形式是轮齿折断和齿面点蚀, 分别依靠齿根弯曲强度和齿面接触疲劳强度来约束, 根据GB3480-1997^[16], 可得到齿面接触和齿根弯曲疲劳强度约束公式分别为:

$\begin{matrix} \begin{matrix} σ_{H} \leq σ_{HP} (28) \\ σ_{F} \leq σ_{FP} (29) \end{matrix} \end{matrix}$

式中:σ _H、σ _F分别为计算接触应力和计算齿根应力; σ _HP、σ _FP分别为许用接触应力和许用齿根应力。

3 优化结果及验证

表2为采用本文优化模型优化前、后的优化变量。为验证本文提出的优化设计方法的有效性, 将原始斜齿轮参数和优化后的参数输入MASTA商用软件中, 对斜齿轮啮合过程中产生的传递误差及其波动值进行计算, 采用的加载载荷为最大载荷1261.5 Nm, 结果如表3所示。

由表3可以看出, 优化后的斜齿轮在啮合过程中的传递误差波动值降低了41%, 同时齿轮的体积降低了1.34%, 这说明本文方法是有效的。

表2 最优化的斜齿轮宏观参数 Table 2 Optimized parameters of helical gear pair

表3 优化前、后齿轮性能对比 Table 3 Performance comparison before and after optimization

4 结论

(1)提出了一种斜齿轮啮合动态传递误差的计算方法, 经验证该方法能够反映传递误差的变化趋势。建立了斜齿轮宏观参数与其啮合过程中的动态传递误差的关系, 为斜齿轮动态传递误差的快速计算提供参考, 也为宏观参数的减振优化设计奠定了基础。

(2)基于斜齿轮动态传递误差计算方法, 提出了变速器斜齿轮宏观参数的减振优化设计模型, 从而达到在变速器齿轮副宏观参数设计阶段就尽量降低冲击振动和可能带来的噪声的目的。优化实例结果表明, 采用本文方法对宏观参数进行优化能够使传递误差波动值降低41%, 同时使体积降低1.34%。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	李宏坤, 郭骋, 房世利, 等. 齿轮箱减振降噪优化设计方法研究[J]. 振动与冲击, 2013, 32(17): 150-154. Li Hong-kun, Guo Cheng, Fang Shi-li, et al. Optimization design method for gearbox's vibration and noise reduction[J]. Journal of Vibration and Shock, 2013, 32(17): 150-154. [本文引用:1]
[2]	李润方, 王建军. 齿轮系统动力学——振动冲击噪声[M]. 北京: 科学出版社, 1997: 383-392. [本文引用:1]
[3]	蒋进科, 方宗德, 苏进展. 宽斜齿轮多目标修形优化设计[J]. 西安交通大学学报, 2014, 48(8): 91-97. Jiang Jin-ke, Fang Zong-de, Su Jin-zhan. Multi-objective optimal and modified design for wide helical gear[J]. Journal of Xi'an Jiaotong University, 2014, 48(8): 91-97. [本文引用:1]
[4]	袁哲, 孙志礼, 王丹, 等. 基于遗传算法的直齿圆柱齿轮修形优化减振[J]. 东北大学学报: 自然科学版, 2010, 31(6): 873-876. Yuan Zhe, Sun Zhi-li, Wang Dan, et al. GA-based optimum profile modification of spur gears for vibration damping[J]. Journal of Northeastern University(Natural Science), 2010, 31(6): 873-876. [本文引用:1]
[5]	吴勇军, 王建军, 韩勤锴, 等. 基于接触有限元分析的斜齿轮齿廓修形与实验[J]. 航空动力学报, 2011, 26(2): 409-415. Wu Yong-jun, Wang Jian-jun, Han Qin-kai, et al. Tooth profile modification of helical gears and experimental study based on finite element contact analysis[J]. Journal of Aerospace Power, 2011, 26(2): 409-415. [本文引用:1]
[6]	赵宁, 杨杰. 高重合度圆柱齿轮传动多目标优化设计[J]. 机械传动, 2012, 36(7): 43-46. Zhao Ning, Yang Jie. Multi-objective optimization design of high contact ratio cylindrical gear drive[J]. Journal of Mechanical Transmission, 2012, 36(7): 43-46. [本文引用:1]
[7]	蒋春明, 阮米庆. 汽车机械式变速器多目标可靠性优化设计[J]. 汽车工程, 2007, 29(12): 1090-1093. Jiang Chun-ming, Ruan Mi-qing. Multi-objective reliability optimal design of automotive mechanical transmission[J]. Automotive Engineering, 2007, 29(12): 1090-1093. [本文引用:1]
[8]	Singh R. Dynamic transmission error prediction of helical gear pair under sliding friction using Floquet theory[J]. Journal of Mechanical Design, 2008, 130(5): 680-682. [本文引用:1]
[9]	常乐浩. 平行轴齿轮传动系统动力学通用建模方法与动态激励影响规律研究[D]. 西安: 西北工业大学机电学院, 2014. Chang Le-hao. A generalized dyamic model for parallel shaft gear transmission and the influences of dynamic excitations[D]. Xi'an: School of Mechanical Engineering, Northwestern Polytechnical Univer-sity, 2014. [本文引用:1]
[10]	李瑰贤, 于广滨, 温建民, 等. 求解齿轮系统非线性动力学微分方程的多尺度方法[J]. 吉林大学学报: 工学版, 2008, 38(1): 75-79. Li Gui-xian, Yu Guang-bin, Wen Jian-min, et al. Method of multiple scales in solving nonlinear dynamic differential equations of gear systems[J]. Journal of Jilin University (Engineering and Technology Edition), 2008, 38(1): 75-79. [本文引用:1]
[11]	李亚鹏, 孙伟, 魏静, 等. 齿轮时变啮合刚度改进计算方法[J]. 机械传动, 2010, 34(5): 22-26. Li Ya-peng, Sun Wei, Wei Jing, et al. Study on the improved algorithm of the time-varying meshing stiffness of gear[J]. Journal of Mechanical Transmission, 2010, 34(5): 22-26. [本文引用:1]
[12]	Wei J, Gao P, Hu X, et al. Effects of dynamic transmission errors and vibration stability in helical gears[J]. Journal of Mechanical Science and Technology, 2014, 28(6): 2253-2262. [本文引用:1]
[13]	Kang J S, Choi Y S. Optimization of helix angle for helical gear system[J]. Journal of Mechanical Science and Technology, 2008, 22(12): 2393-2402. [本文引用:1]
[14]	刘志峰, 张志民, 张敬莹, 等. 基于多项式的等高齿锥齿轮时变啮合刚度建模[J]. 吉林大学学报: 工学版, 2013, 43(4): 939-944. Liu Zhi-feng, Zhang Zhi-min, Zhang Jing-ying, et al. Modelling of high-spiral bevel gear mesh stiffness based on polynomial[J]. Journal of Jilin University(Engineering and Technology Edition), 2013, 43(4): 939-944. [本文引用:1]
[15]	符升平, 项昌乐, 姚寿文, 等. 基于刚柔耦合动力学的齿轮传动系统动态特性[J]. 吉林大学学报: 工学版, 2011, 41(2): 382-386. Fu Sheng-ping, Xiang Chang-le, Yao Shou-wen, et al. Dynamic characteristic of gear transmission system based on rigid and flexible coupled dynamics[J]. Journal of Jilin University(Engineering and Technology Edition), 2011, 41(2): 382-386. [本文引用:1]
[16]	GB/T3480-1997. 渐开线圆柱齿轮承载能力计算方法[S]. [本文引用:1]

2013

0.0

. 2013, 32(17):150-154 DOI:doi:10.3969/j.issn.1000-3835.2013.17.029

Optimization design method for gearbox's vibration and noise reduction

齿轮箱减振降噪优化设计方法研究

Li Hong-kun , Guo Cheng , Fang Shi-li

李宏坤, 郭骋, 房世利

The mode contribution and the panel acoustic contribution analysis of an experimental gearbox are discussed in this research. The main contribution to the modal and the main panel of the noise radiation are determined. Then, the relationship between the surface vibration and radiated noise of the gearbox is investigated according to the finite element method combined with the vibration velocity method. On the basis of above investigation, the radiated sound power level of the main panels of the gearbox is calculated. This parameter and the natural frequency of the main contribution mode could be an objective function of the gearbox vibration and noise reduction. Optimization program which is wrote by APDL. According to the simulation analysis, an optimal thickness for the gearbox can be obtained. The results of this paper show that this method is effective for noise and vibration reduction. It is helpful for the optimization design of the gearbox.

对某试验用齿轮箱进行了模态贡献量与面板声学贡献量分析，确定齿轮箱运行过程中箱体振动主要贡献模态和噪声辐射面板；结合振速法原理，对箱体表面振动与辐射噪声的关系进行了分析，实现基于有限元方法对箱体进行稳态振动响应求解与主要面板辐射声功率级的计算；将主要贡献模态固有频率和面板辐射声功率级作为目标函数，编制APDL的优化求解程序对齿轮箱箱体实现了减振降噪优化，得到了箱体各壁面的最优壁厚组合.结果表明，该方法具有很好的减振降噪效果，为齿轮箱的优化设计提供了借鉴意义.

... 在箱体整体噪声方面,李宏坤等^[1]在对某齿轮箱进行模态贡献量和面板声学贡献量分析的基础上,将主要固有频率和面板声功率级作为目标函数,应用有限元软件进行了箱体厚度的减振优化设计 ...

1997

0.0

... 关于齿轮副的设计方面,当齿轮的类型、材料都确定后,影响振动和噪声的指标包括齿轮几何宏观参数、微观修形方式和修形量两个方面^[2] ...

2014

0.0

. 2014, 48(8):91-97 DOI:doi:10.7652/xjtuxb201408016

Multi-objective optimal and modified design for wide helical gear

宽斜齿轮多目标修形优化设计

Jiang Jin-ke , Fang Zong-de , Su Jin-zhan.

蒋进科, 方宗德, 苏进展

通过理论齿面叠加修形曲面方法来设计斜齿轮修形齿面,根据齿轮接触分析、承载接触分析计算得到承载变形、接触线上的离散载荷及啮合刚度,应用弹流润滑剂理论确定离散点的局部摩擦系数,并通过Blok闪温公式获得齿面闪温,建立斜齿轮啮合型弯-扭-轴-摆10自由度动力学模型;以承载传动误差幅值、齿面闪温最小、齿面载荷均匀及振动加速度最小为目标,通过改进的粒子群优化算法确定了最佳修形齿面.结果表明:修形后齿轮副重合度增加,载荷均匀,齿面闪温分布明显改善;随转速、载荷的增加,啮合冲击逐渐增大,且随转速增加, 啮合冲击激励较刚度激励的振动更加明显,因此共振的敏感性降低,多载荷承载传动误差幅值反映了振动随裁荷变化趋势;修形后传动误差幅值、啮合冲击降低,因此有效降低了系统振动.

... 微观修形对齿轮的啮入、啮出冲击激励有很大影响,是目前对齿轮振动和噪声优化设计的主要手段^[3,4,5] ...

2010

0.0

. 2010, 31(6):873-876 DOI:doi:-

GA-based optimum profile modification of spur gears for vibration damping

基于遗传算法的直齿圆柱齿轮修形优化减振

Yuan Zhe , Sun Zhi-li , Wang Dan

袁哲, 孙志礼, 王丹

摘　要：为了准确地确定齿轮修形参数,在分析传递误差对齿轮振动影响的基础之上,依靠有限元模型模拟了一对修形齿轮的啮合过程,并引入遗传算法,以减小齿轮的传递误差的波动为目标,对齿轮的修形参数进行了高精度的优化设计.研究表明,该方法确定的齿轮修形参数精确、有效,能够避免啮合冲击,并且能大幅度减小齿轮的动态传递误差波动,为无声齿轮的研究指出了新的设计方法.

... 微观修形对齿轮的啮入、啮出冲击激励有很大影响,是目前对齿轮振动和噪声优化设计的主要手段^[3,4,5] ...

2011

0.0

. 2011, 26(2):409-415

Tooth profile modification of helical gears and experimental study based on finite element contact analysis

基于接触有限元分析的斜齿轮齿廓修形与实验

Wu Yong-jun , Wang Jian-jun , Han Qin-kai

吴勇军, 王建军, 韩勤锴

研究了基于接触有限元分析的斜齿轮精确齿廓修形设计,并进行了振动对比验证实验.在AN-SYS环境下建立了精确的斜齿轮副接触有限元分析模型,并通过有限元接触分析,以直接提取的啮合线方向综合弹性变形作为齿廓修形设计的依据,精确确定了斜齿轮副的齿廓修形量及修形设计方案;根据所确定的齿廓修形设计方案,设计并建立了台架对比实验系统,进行了多种转速和载荷工况下的振动对比实验,并分析了齿廓修形设计方案的实际减振降噪效果和特点.研究表明:提出的斜齿轮精确齿廓修形设计方案是合理的,而且具有很好的减振降噪效果,两种评价指标下最大分别减振11.28dB和4.69dB.

... 微观修形对齿轮的啮入、啮出冲击激励有很大影响,是目前对齿轮振动和噪声优化设计的主要手段^[3,4,5] ...

2012

0.0

. 2012, 36(7):43-46

Multi-objective optimization design of high contact ratio cylindrical gear drive

高重合度圆柱齿轮传动多目标优化设计

Zhao Ning , Yang Jie.

赵宁, 杨杰

以重合度最大、体积最小、弯曲强度相等为目标函数,建立了圆柱齿轮传动多目标优化设计数学模型,采用带精英策略的快速非支配排序遗传算法(NSGA-Ⅱ)进行优化求解。对高速重载斜齿圆柱齿轮传动进行了高重合度优化设计,得到了Parteto最优解,并从中选择了一个优化方案与原始方案进行对比,结果显示高重合度圆柱齿轮传动的强度有明显提高,体积也有一定的减小。

... 在宏观参数设计阶段,基本是通过经验和定性分析来确定和调整齿轮几何宏观参数,使得齿轮的噪声品质满足要求,或是单纯地通过提高重合度来优化齿轮振动和噪声品质^[6,7] ...

2007

0.0

. 2007, 29(12):1090-1093 DOI:doi:10.3321/j.issn:1000-680x.2007.12.017

Multi-objective reliability optimal design of automotive mechanical transmission

汽车机械式变速器多目标可靠性优化设计

Jiang Chun-ming , Ruan Mi-qing.

蒋春明, 阮米庆

以某轿车变速器为例,根据汽车动力性要求,在保证零件强度和刚度可靠性的条件下,按变速器齿轮系体积最小和传动齿轮重合度最大建立了变速器的多目标可靠性优化设计的数学模型,然后应用MATLAB优化工具箱进行联合优化设计计算.设计结果表明:该数学模型正确有效,采用多目标可靠性优化设计方法可以缩短汽车变速器的设计周期,减小其体积并改善传动平稳性.

2008

0.0

... 齿轮动力学研究^[8]表明,齿轮箱系统的振动很大程度上取决于各齿轮副的动态传递误差 ...

2014

0.0

. 2014, :-

平行轴齿轮传动系统动力学通用建模方法与动态激励影响规律研究[D]

Chang Le-hao.

常乐浩

齿轮传动系统是由齿轮副、传动轴、轴承和箱体组成的复杂弹性机械系统。由于结构紧凑、效率高和寿命长等优点，齿轮传动在国家工业部门各领域均有着广泛的应用。齿轮啮合过程中的弹性变形、制造误差和啮合冲击等因素对齿轮的接触特性和动态性能有着很大的影响。随着对机械系统性能要求的提高，齿轮传动正朝着高速、重载、低噪声的方向发展。因此，研究不同动态激励因素和工作状况对齿轮系统动态响应的影响规律，对准确把握齿轮系统动力学本质特征以及低振动噪声的齿轮传动装置设计具有重要的理论指导意义和工程实用价值。　　本文建立了计算齿轮传递误差和...

... 在设计变速器时,一般通过MASTA等变速器设计专用软件或ANSYS等有限元软件计算齿轮的传递误差,但MASTA软件不能对传递误差进行优化设计,需要手动修改参数反复尝试,而有限元软件建模复杂且计算时间长^[9] ...

2008

0.0

. 2008, 38(1):75-79

Method of multiple scales in solving nonlinear dynamic differential equations of gear systems

求解齿轮系统非线性动力学微分方程的多尺度方法

Li Gui-xian , Yu Guang-bin , Wen Jian-min

李瑰贤, 于广滨, 温建民

首先建立了描述齿轮系统扭转振动的动力学分析模型,并推导出综合考虑时变啮合刚度、齿侧间隙、动态传递误差等非线性因素的齿轮系统非线性动力学的统一微分方程。介绍了用于求解齿轮系统非线性动力学微分方程的多尺度方法的原理,并推导了频率响应方程。利用多尺度方法获得的近似解析解与直接进行数值积分所获得的精确解吻合得较好,表明多尺度方法是求解复杂非线性微分方程最有效的方法之一。

... 李瑰贤等^[10]提出采用多尺度法近似求解齿轮系非线性微分方程 ...

2010

0.0

. 2010, 34(5):22-26 DOI:doi:10.3969/j.issn.1004-2539.2010.05.006

Study on the improved algorithm of the time-varying meshing stiffness of gear

齿轮时变啮合刚度改进计算方法

Li Ya-peng , Sun Wei , Wei Jing

李亚鹏, 孙伟, 魏静

齿轮时变啮合刚度是齿轮系统动力方程的重要基础参数,针对目前时变啮合刚度主要利用有限元方式计算,效率偏低的问题,以及解析法石川公式仅考虑齿轮轮齿刚度,未考虑齿轮轮体刚度,容易在齿轮动力学分析中引入高次谐波激励的不足,本文在详细介绍解析算法石川公式中重要参数算法的基础上提出改进的石川公式,为齿轮动力方程提供一个整体意义上的时变啮合刚度计算方法.同时介绍了多齿啮合时齿轮综合时变啮合刚度的计算方法.

... 传统石川法或改进石川法是一种基于材料力学理论的快速计算直齿轮时变啮合刚度和设计传递误差的较好方法^[11],但该方法只适用于直齿轮 ...

2014

0.0

... Wei等^[12]建立了六自由度斜齿轮啮合动力学模型,用于计算齿轮啮合的传递误差,并用该模型分析了齿轮重合度、轴支撑刚度、啮合阻尼等齿轮参数对动态传递误差的影响 ...

2008

0.0

... Kang等^[13]采用有限元方法建立了斜齿轮的传递误差计算模型,并用该模型计算不同螺旋角下的齿轮重合度和传递误差,建立了重合度、传递误差与螺旋角之间的关系 ...

2013

0.0

. 2013, 43(4):939-944 DOI:doi:10.7964/jdxbgxb201304016

Modelling of high-spiral bevel gear mesh stiffness based on polynomial

基于多项式的等高齿锥齿轮时变啮合刚度建模

Liu Zhi-feng , Zhang Zhi-min , Zhang Jing-ying

刘志峰, 张志民, 张敬莹

We present a new time-varying mesh stiffness model using polynomial function with regard to the time-varying mesh stiffness of the high-bevel gear of a radar device. By analyzing the revolution speed, load torque and damping factor, we build the mesh stiffness model and the nonlinear dynamic equations of the high-bevel gear. We compare the proposed mesh stiffness model with traditional rime-varying mesh stiffness model of multi-order harmonic superposition and reference data model of time-varying comprehensive stiffness. It is shown that, with small damping and overload, the proposed model is much closer to the actual characteristics of the time-varying stiffness. This model lays a foundation to study the gear transmission dynamics, such as vibration damping, noise reduction, smooth transmission and other aspects with small damping and overload.

针对某型雷达装置的等高齿锥齿轮在啮合时的时变啮合刚度,提出一种多项式函数展开的时变啮合刚度新模型。通过转速、负载扭矩、阻尼因子系数分析,构建了多项式函数展开的时变啮合刚度模型,建立了等高齿锥齿轮的非线性动力学方程。将本文建立的时变啮合刚度模型与传统的多阶简谐波叠加形式的时变啮合刚度模型以及综合刚度参考数据模型进行分析对比,发现在小阻尼、重载工况下这种多项式形式的时变啮合刚度模型能更贴近于时变啮合刚度的实际特性,该模型为齿轮传动的减振、降噪、平稳传动等方面的动力学研究打下基础。

... 对于其他齿轮形式,刘志峰等^[14]针对等高齿锥齿轮提出将时变啮合刚度表示为啮合中心沿齿面法向位移的多项式函数 ...

2011

0.0

. 2011, 41(2):382-386

Dynamic characteristic of gear transmission system based on rigid and flexible coupled dynamics

基于刚柔耦合动力学的齿轮传动系统动态特性

Fu Sheng-ping , Xiang Chang-le , Yao Shou-wen

符升平, 项昌乐, 姚寿文

摘　要：为得到齿轮轴系响应的动态特性，从柔体动力学基本理论出发，系统分析了刚柔耦合动力学模型的机理，建立了多级齿轮传动刚柔耦合的虚拟样机。此模型能综合考虑传动轴各方向上的柔性特征、湿式换档离合器动态特性以及齿轮时变啮合力对轴类零件动态响应的影响。仿真结果证明了通过虚拟样机技术获取载荷谱的可行性，可用于轴的疲劳寿命预测以及齿轮箱体的振动研究。

... 此外,也有少数研究建立了齿轮传动系整体动力学模型,如符升平等^[15]建立了多级齿轮传动刚柔耦合动力学模型,综合考虑了传动轴各向柔性、湿式离合器动特性及齿轮时变啮合力对轴类零件动态响应的影响 ...

0.0

... 齿轮最重要的两种失效形式是轮齿折断和齿面点蚀,分别依靠齿根弯曲强度和齿面接触疲劳强度来约束,根据GB3480-1997^[16],可得到齿面接触和齿根弯曲疲劳强度约束公式分别为: ...