基于奇异谱分析和CKF-LSSVM的短时交通流量预测

引用本文

商强, 杨兆升, 张伟, 邴其春, 周熙阳. 基于奇异谱分析和CKF-LSSVM的短时交通流量预测. 吉林大学学报:工学版, 2016, 46(6): 1792-1798
SHANG Qiang, YANG Zhao-sheng, ZHANG Wei, Bing Qi-chun, ZHOU Xi-yang. Short-term traffic flow prediction based on singular spectrum analysis and CKF-LSSVM. Journal of Jilin University Engineering and Technology Edition, 2016, 46(6): 1792-1798 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201606006
Permissions

基于奇异谱分析和CKF-LSSVM的短时交通流量预测

商强¹, 杨兆升^1,^2,³, 张伟^1,^2,⁴, 邴其春¹, 周熙阳¹

1.吉林大学交通学院,长春 130022

2.吉林大学汽车仿真与控制国家重点实验室,长春 130022

3.吉林大学吉林省道路交通重点实验室,长春 130022

4.山东高速公路股份有限公司,济南 250014

张伟(1978-),男,高级工程师,在站博士后.研究方向:智能交通系统理论与技术.E-mail:z_wei@126.com

作者简介:商强(1987-),男,博士研究生.研究方向:智能交通系统理论与技术.

基金项目:国家科技支撑计划项目(2014BAG03B03); 国家自然科学基金项目(51308248, 51408257, 51308249); 山东省省管企业科技创新项目(20122150251-1)

摘要

为了提高短时交通流预测的精度,提出了基于奇异谱分析和组合核函数最小二乘支持向量机(CKF-LSSVM)的短时交通流预测模型。首先,采用奇异谱分析方法,滤除交通流序列的噪声成分。然后,使用降噪后的交通流数据训练CKF-LSSVM,并通过粒子群优化算法确定模型参数。最后,以厦门市的实测数据为基础,对预测模型进行实验验证和对比分析。结果表明:本文所构建模型具有较好的预测效果,能够有效提高短时交通流预测精度。

关键词: 交通运输系统工程; 短时交通流预测; 奇异谱分析; 支持向量机; 组合核函数

中图分类号:U491 文献标志码:A 文章编号:1671-5497(2016)06-1792-07

Short-term traffic flow prediction based on singular spectrum analysis and CKF-LSSVM

SHANG Qiang¹, YANG Zhao-sheng^1,^2,³, ZHANG Wei^1,^2,⁴, Bing Qi-chun¹, ZHOU Xi-yang¹

1.College of Transportation, Jilin University,Changchun 130022,China

2.State Key Laboratory of Automotive Simulation and Control,Jilin University,Changchun 130022, China

3.Jilin Province Key Laboratory of Road Traffic,Jilin University, Changchun 130022,China

4.Shandong High-speed Co.,Ltd.,Ji'nan 250014,China

Abstract

In order to improve the accuracy of short-time traffic flow prediction, a short-term traffic flow prediction model based on singular spectrum analysis and Combined Kernel Function (CKF) Least Square Support Vector Machine (LSSVM) is proposed. Singular spectrum analysis technology is used to filter out the noise of traffic time series. Then, the processed traffic flow data are used to train the CKF-LSSVM, and the parameters of the model are determined by particle swarm optimization algorithm. Finally, validation and comparative analysis of the model are carried out using the measured in Xiamen, China. Experimental results indicate that the proposed model has good prediction performance and can effectively improve the accuracy of short-time traffic flow prediction.

Key words: engineering of communication and transportation system; short-term traffic flow prediction; singular spectrum analysis; support vector machine; combined kernel function

Show Figures

0 引言

短时交通流预测是智能交通系统(ITS)研究的重要组成部分。实时、准确的短时交通流预测能够直接应用于ITS子系统中^[1], 如先进的交通管理系统(ATMS)和先进的出行者信息系统(ATIS)。因此, 短时交通流预测受到了广泛的关注。已有文献提出了大量的短时交通流预测模型和方法, 大致可以分为3类:①基于交通流模拟的预测方法, 通过模拟交通流运行状态, 预测其未来的发展趋势。宏观交通流模拟是将交通流比拟成水流, 借鉴流体动力学的相关理论分析交通流。微观交通流模拟则考虑的是单车行为以及路网中车与车之间的相互作用^{[2, 3]}。②基于统计学的预测模型。通过数据集的回归拟合和参数的选择优化, 以实现交通预测。例如:局部线性回归模型、ARMA模型和Kalman滤波模型^{[4, 5, 6]}。③基于数据挖掘的预测方法。这类方法一般没有固定的形式, 而是以数据驱动, 通过智能算法寻找历史数据的变化趋势, 进而预测未来数据。例如人工神经网络和支持向量机^{[7, 8]}。与前两类方法相比, 基于数据挖掘的预测方法没有对模型做出诸多假设(例如假设观测时间序列是平稳的, 残差服从正态分布, 预先给定模型的结构), 因而具有更好的适用性。最小二乘支持向量机(Least squares support vector machine, LSSVM)是支持向量机的一种改进形式, 学习速度更快^[9]。然而, 在数据采集和传输过程中, 不可避免地受到交通检测器自身软(硬)件故障、外界环境异常(如电磁干扰)等因素的影响, 导致采集数据中含有噪声成分。如果将观测数据直接用于LSSVM的训练, 则一定程度上降低了模型的泛化能力。奇异谱分析(Singular spectrum analysis, SSA)是一种有效的降噪方法, 已在水文预测、电力负荷预测和天气预测等方面有了相关应用^[10]。文献^[11]使用多种方法处理GPS坐标数据, 结果表明SSA降噪效果优于小波和经验模态分解方法。

本文提出一种基于SSA和组合核函数最小二乘支持向量机(Combined kernel function least squares support vector machine, CKF-LSSVM)的短时交通流预测模型(SSA-CKF-LSSVM)。首先, 通过SSA将交通流序列分解和重构, 得到原序列的趋势成分、振荡成分和噪声成分。然后, 使用除去噪声成分的交通流数据训练CKF-LSSVM, 并通过粒子群优化算法确定模型参数组合。最后, 利用实测交通流数据, 将新建模型与其他模型的预测效果进行对比。

1 奇异谱分析

将长度为N的一维时间序列T=(x₁, x₂, …, x_N)转化为一系列的L维向量:X_i=(x_i, x_i+₁, …, x_i+L-₁)^T。其中, L(1< L< N)称为窗口长度(Window length)。由K个向量X_i(i=1, …, K=N-L+1)构成轨迹矩阵X(L× K):

$\begin{matrix} X = [\begin{matrix} x_{1} & x_{2} & \dots & x_{K} \\ x_{2} & x_{3} & \dots & x_{K + 1} \\ ⋮ & ⋮ & ⋮ \\ x_{L} & x_{L + 1} & \dots & x_{N} \end{matrix}] \end{matrix}$ (1)

将X进行奇异值分解:

$\begin{matrix} X = U \cdot S \cdot V^{T} \end{matrix}$ (2)

式中:S为矩阵X的奇异值, 等价于矩阵XX^T特征值的平方根; U为X的左奇异向量, 等价于矩阵XX^T的特征向量; V为矩阵X的右奇异向量, 等价于X^TX的特征向量。

将时间序列T的元素由奇异谱分析展开:

$\begin{matrix} x_{i + j} = \overset{M}{\sum_{k = 1}} a_{ik} E_{kj} \end{matrix}$ (3)

式中:i=1, …, K; j=1, …, M; E_kj=U为XX^T的特征向量, E称为时间经验正交函数; a_ik为通过式(4)求得的时间主成分:

$\begin{matrix} a_{ik} = \overset{M}{\sum_{j = 1}} x_{i + j} E'_{kj} \end{matrix}$ (4)

x_i的第k个主成分记作 $\begin{matrix} X_{i}^{k} \end{matrix}$ , 通过第k个时间经验正交函数和时间主成分重构得到, 如式(5)所示:

$\begin{matrix} X_{i}^{k} = \{\begin{matrix} (\overset{L}{\sum_{j = 1}} a_{ij, k} E_{kj}) / L, L \leq i \leq K \\ (\overset{i}{\sum_{j = 1}} a_{ij, k} E_{kj}) / i, 1 \leq i \leq L - 1 \\ \frac{1}{N - i + 1} \overset{L}{\sum_{j = i - n + m}} a_{ij, k} E_{kj}, \\ N - L + 2 \leq i \leq N \end{matrix} \end{matrix}$ (5)

根据式(6)选择对应较大奇异值的m个成分相加, 所得到 $\begin{matrix} {\tilde{x}}_{i} \end{matrix}$ 近似代表x_i:

$\begin{matrix} {\tilde{x}}_{i} = \overset{m}{\sum_{k = 1}} X_{i}^{k}, i = 1, \dots, N \end{matrix}$ (6)

因此, 重构过程很大程度上滤除那些对应较小奇异值的噪声成分。

2 组合核函数LSSVM

设D=(x_i, y_i), i=1, …, N为样本集, x_i∈ R^m为输入; y_i∈ R为相应输出。回归函数为:

$\begin{matrix} f (x) = ω^{T} φ (x) + b \end{matrix}$ (7)

式中:φ (· )为非线性函数; ω 为权向量; b为偏置量。

LSSVM回归的优化目标函数为:

$\begin{matrix} \{\begin{matrix} \min_{ω, b, e} J_{1} (ω, e) = μ E_{W} + ζ E_{D} = \frac{1}{2} μ ω^{T} ω + \frac{1}{2} ζ \overset{N}{\sum_{i = 1}} e_{i}^{2} \\ s.t. y_{i} = ω^{T} φ (x) + b + e_{i} \end{matrix} \end{matrix}$ (8)

式中:e_i为误差变量; μ 和ζ 为可变参数; E_W= $\begin{matrix} \frac{1}{2} \end{matrix}$ ω ^Tω ; E_D= $\begin{matrix} \frac{1}{2} \end{matrix} \begin{matrix} \overset{N}{\sum_{i = 1}} \end{matrix} \begin{matrix} e_{i}^{2} \end{matrix}$ = $\begin{matrix} \frac{1}{2} \end{matrix} \begin{matrix} \overset{N}{\sum_{i = 1}} \end{matrix} \begin{matrix} {[y_{i} - ω^{T} φ (x) + b]}^{2} \end{matrix}$ 。

为了求解上述优化问题, 因此构建Lagrange函数:

$\begin{matrix} \begin{matrix} L (ω, b, e, α) = J_{1} (ω, e) - \\ \overset{N}{\sum_{i = 1}} α_{i} \{ω^{T} φ (x) + b + e_{i} - y_{i}\} (9) \end{matrix} \end{matrix}$

式中:α _i为Lagrange乘子, 由KKT条件可得:

$\begin{matrix} \{\begin{matrix} \frac{\partial L}{\partial ω} = 0 \to ω = \overset{N}{\sum_{i = 1}} α_{i} φ (x_{i}) \\ \frac{\partial L}{\partial b} = 0 \to \overset{N}{\sum_{i = 1}} α_{i} = 0 \\ \frac{\partial L}{\partial e_{i}} = 0 \to α_{i} = γ e_{i} \\ \frac{\partial L}{\partial α_{i}} = 0 \to ω^{T} φ (x_{i}) + b + e_{i} - y_{i} = 0 \end{matrix} \end{matrix}$ (10)

式中:惩罚系数γ =ζ /μ 。消除ω 和e_i后, 原优化问题变为:

$\begin{matrix} [\begin{matrix} 0 & l^{T} \\ l & Ω_{ij} + \frac{1}{γ} I \end{matrix}] [\begin{matrix} b \\ a \end{matrix}] = [\begin{matrix} 0 \\ Y \end{matrix}] \end{matrix}$ (11)

式中:Ω _ij=φ (x_i)^Tφ (x_j)=K(x_i, x_j); l=[1, …, 1]^T; α =[α ₁, …, α _N]^T; Y=[y₁, …, y_N]^T。

通过式(11)求出α 和b, 那么LSSVM回归模型为:

$\begin{matrix} f (x) = \overset{N}{\underset{i = 1}{\sum α_{i}}} K (x, x_{i}) + b \end{matrix}$ (12)

式中:K $\begin{matrix} (x, x_{i}) \end{matrix}$ 为核函数, 需符合Mercer条件, 如RBF核函数、线性核函数和多项式核函数等。其中, RBF核函数为:

$\begin{matrix} K (x, x_{i}) = \exp [- ‖ x - x_{i} ‖^{2} / (2 σ^{2})], σ > 0 (13) \end{matrix}$

多项式核函数为:

$\begin{matrix} K (x, x_{i}) = {(x x_{i} + 1)}^{q} \end{matrix}$ (14)

式中:q为参数。

RBF核函数在实际应用中最为广泛, 是一种典型局部核函数, 学习能力较强, 泛化能力较弱; 而全局核函数与之相反^[12]。多项式核函数是常用的全局核函数。这两种核函数的有机组合能够提高LSSVM模型预测精度。因此, 本文模型采用多项式函数(K_poly)和RBF核函数(K_RBF)的线性组合核函数K_com, 即:

$\begin{matrix} K_{com} = ρ K_{RBF} + (1 - ρ) K_{poly} \end{matrix}$ (15)

式中:ρ 为参数。

3 优化模型参数

组合核函数LSSVM参数包括:惩罚系数γ 、RBF核函数参数σ 、多项式核函数参数q和组合核函数系数ρ 。通过粒子群寻优算法(Particle swarm optimization, PSO)确定模型参数组合。PSO是一种启发式全局寻优算法, 其基本原理是:假设d维搜索空间中的第i个微粒的速度v_i=(v_i₁, v_i₂, …, v_id), 位置x_i=(x_i₁, x_i₂, …, x_id)。通过评价各微粒的适应度, 确定t时刻每个微粒所经过的最佳位置p_i=(p_i₁, p_i₂, …, p_id)和种群中已找到的最优位置p_g=(p_g₁, p_g₂, …, p_gd)。根据式(16)更新微粒的速度, 根据式(17)更微粒的位置:

$\begin{matrix} \begin{matrix} v_{i, j} (t + 1) = w v_{i, j} (t) + c_{1} rand (p_{i, j} - x_{i, j} (t)) + \\ c_{2} rand (p_{g, i} - x_{i, j} (t)) (16) \\ x_{i, j} (t + 1) = x_{i, j} (t) + v_{i, j} (t + 1) (17) \\ j = 1, 2, \dots, d \end{matrix} \end{matrix}$

式中:w为惯性权值; c₁和c₂为加速因子; rand为0到1之间的随机数, 通过设置微粒的速度区间 $\begin{matrix} [v_{\min}, v_{\max}] \end{matrix}$ 和位置范围 $\begin{matrix} [x_{\min}, x_{\max}] \end{matrix}$ 可适当控制微粒移动。

惯性权值w代表粒子前一次迭代速度对当前迭代速度的影响, 较大的w全局搜索能力较好, 而较小的w局部搜索能力较好。不断调整惯性权值, 符合算法进化特性。因此, 使用线性递减的惯性权值公式:

$\begin{matrix} w = w_{start} - \frac{w_{start} - w_{end}}{T_{\max}} T \end{matrix}$ (18)

式中:w_start为起始惯性权值; w_end为终止惯性权值; T为当前迭代次数; T_max为最大迭代次数。

SSA-CKF-LSSVM模型构建和优化流程为:

Step1 采用奇异谱分析, 滤除原交通流时间序列的噪声成分。

Step1.1 嵌入:确定延迟窗口长度L。

Step1.2 奇异值分解:获得L个奇异值。

Step1.3 分组:将奇异值从大到小排序, 后面的奇异值较小, 且变化不大, 对应噪声成分。

Step1.4 对角平均:根据奇异值分组, 重构降噪交通流量序列。

Step2 使用降噪后数据, 构建训练样本集。

Step3 粒子群算法优化模型参数。

Step3.1 模型参数初始化, 粒子群参数初始化。

Step3.2 确定适应度函数。

Step3.3 计算并比较适应度, 更新微粒速度和位置。

Step3.4 满足停止条件, 输出模型参数。

4 实例分析

	Figure Option View Download New Window
	图1 交通流量时间序列Fig.1 Traffic flow time series

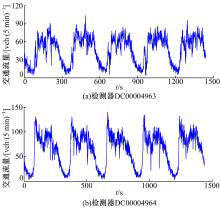
数据来源于厦门市莲前西路的地磁检测器, 检测器统计时间间隔为5 min, 采集连续5个工作日(2015年1月5日~2015年1月9日)的交通流量数据。编号为DC00004963的检测器和编号为DC00004964的检测器分别采集由西向东和由东向西的交通流量数据, 所得交通流量时间序列如图1所示。前4天交通流量用于SSA-CKF-LSSVM模型的构建, 第5天交通流量用于模型预测效果的验证和对比分析。

	Figure Option View Download New Window
	图2 交通流量序列的奇异谱Fig.2 Singular spectrum of traffic flow time series

下面将以DC00004963号检测器数据为例详细说明模型构建和优化的过程。

4.1 奇异谱分析

在奇异谱分析中, 窗口长度L是唯一需要确定的参数。此处L取288, 即一天交通流量序列的长度。所得L个奇异值按从大到小顺序排列称为奇异谱。前72个(总共288个)奇异值按从大到小顺序排列的曲线如图2所示。从第36个奇异值开始, 后面奇异值变化缓慢, 因此36~288个奇异值对应着噪声成分。最大奇异值对应着趋势成分, 2~35个奇异值对应着振荡成分, 例如(2, 3)、(4, 5)、(6, 7)和(8, 9)等, 它们成对存在, 奇异值大小相同或相近, 也说明它们对应着振荡成分。

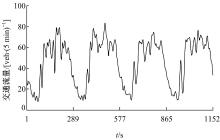
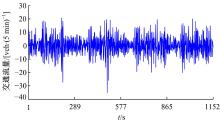
图3为前9个奇异值(特征三元组)对应的重构序列及其贡献率。第1~35个奇异值对应重构的序列如图4所示, 累积贡献率为98.390%。图5为第36~288个奇异值对应的重构序列, 即噪声序列。由图3~图5可知:第1个奇异值对应的重构序列为趋势成分, 贡献率为81.104%; 第2~35个奇异值对应的重构序列为振荡成分, 累积贡献率为17.286%; 第36~288个奇异值对应的重构序列为噪声成分, 具有较高的频率, 累积贡献率仅为1.610%。

	Figure Option View Download New Window
	图3 前9个奇异值对应的重构序列及其贡献率Fig.3 Reconstructed traffic series of first 9 singular value

4.2 组合核函数LSSVM的参数优化

将预测值作为模型输出, 预测值前两小时的交通流量序列作为模型输入, 以此实现交通流量的单步预测, 即使用历史数据滚动预测下一时刻交通流量。使用前4天SSA降噪交通流量数据构建训练集, 包括了1128组输入-输出关系。

	Figure Option View Download New Window
	图4 重构交通流量序列Fig.4 Reconstructed traffic time series

	Figure Option View Download New Window
	图5 噪声序列Fig.5 Noisy time series

采用PSO算法优化模型参数, 包括惩罚系数γ 、RBF核函数参数σ 、多项式核函数参数q和组合核函数系数ρ , 共计4个参数, 即粒子群维数d=4。设置种群数量为20; 加速因子c₁=1.5; c₂=1.7; 最大迭代次数为T_max=100; 最大速度v_max=2; 起始惯性权重w_start=0.9; 终止惯性权重w_end=0.4。模型参数:γ ∈ (0, 1000], σ ∈ (0, 100], ρ ∈ [0, 1], q∈ $\begin{matrix} (0, 1, \dots, 10) \end{matrix}$ 。适应度函数fitness为平均百分比误差(MAPE):

$\begin{matrix} fitness = MAPE = \frac{1}{n} \overset{n}{\sum_{i = 1}} |\frac{y_{i} - {\hat{y}}_{i}}{y_{i}}| \end{matrix}$ (19)

式中: $\begin{matrix} {\hat{y}}_{i} \end{matrix}$ 为第i时刻的预测值; y_i为第i时刻的真实值; n为样本量。

	Figure Option View Download New Window
	图6 PSO寻优适应度曲线Fig.6 Fitness curve of PSO

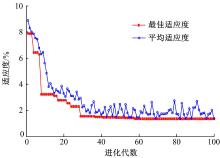
为了更具有统计意义, 采用5折交叉验证, 完成模型训练和参数优化。图6为适应度变化曲线, 模型的优化参数组合:γ =76.63, σ =8.57, ρ =0.83, q=3。

4.3 预测结果及分析

为了更好地分析SSA-CKF-LSSVM模型的预测效果, 引入ARMA模型、CKF-LSSVM模型和SSA-BPNN模型作对比。其中, ARMA模型使用前提是预测平稳时间序列。对于非平稳序时间序列, 须要通过差分将其转化为平稳时间序列。其他几个模型均属于智能学习模型, 需要较多的训练样本。使用原始交通流量数据构建ARMA模型和CKF-LSSVM模型。使用SSA降噪后交通流量数据构建SSA-BPNN模型。其中, CKF-LSSVM模型参数的优化同样使用PSO算法。预测效果评价指标包括:平均绝对误差(MAE)、平均相对百分比误差(MAPE)、均方误差(MSE)和均等系数(EC), 计算公式如下:

$\begin{matrix} \begin{matrix} MAE = \frac{1}{n} \overset{n}{\sum_{i = 1}} |y_{i} - {\hat{y}}_{i}| (20) \\ MAPE = \frac{1}{n} \overset{n}{\sum_{i = 1}} |\frac{y_{i} - {\hat{y}}_{i}}{y_{i}}| (21) \\ MSE = \frac{1}{n} \overset{n}{\sum_{i = 1}} (y_{i} - {\hat{y}}_{i})^{2} (22) \\ EC = 1 - \frac{\sqrt[]{\overset{n}{\sum_{i = 1}} (y_{i} - {\hat{y}}_{i})^{2}}}{\sqrt[]{\overset{n}{\sum_{i = 1}} y_{i}^{2}} + \sqrt[]{\overset{n}{\sum_{i = 1}} {\hat{y}}_{i}^{2}}} (23) \end{matrix} \end{matrix}$

MAE、MAPE、MSE越小, 说明预测误差越小, 预测效果越好。均等系数EC越接近于1, 说明预测值与实际值之间拟合度越好, 实际值与预测值之间有着更为相似的演化趋势。

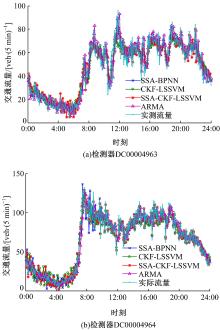
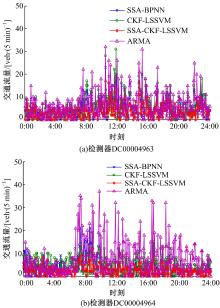
各模型预测效果曲线如图7所示, 绝对误差曲线如图8所示, 预测性能的评价指标值如表1所示。由图7可知, SSA-CKF-LSSVM模型预测曲线与实测曲线的拟合效果最佳; 模型的EC值为0.96(均值), 最接近于1, 同样说明拟合效果最佳; 而ARMA模型EC值仅为0.87(均值), 这是因为该预测模型具有一定的滞后性。由图8可知, SSA-CKF-LSSVM模型的绝对误差波动范围最小, 表明该模型预测稳定性较好, 特别是在交通流变化相对剧烈时(如7:00~9:00时段)。由表1可知, SSA-CKF-LSSVM模型的三项误差(MAE、MAPE、MSE)均低于其他模型。综上, 基于奇异谱分析和组合核函数LSSVM的预测模型预测性能良好, 能提高短时交通流量的预测精度。

	Figure Option View Download New Window
	图7 各模型交通流量的预测效果Fig.7 Effect of traffic flow prediction models

	Figure Option View Download New Window
	图8 各模型预测的绝对误差Fig.8 Absolute error of traffic flow prediction models

表1 各预测模型的评价指标值 Table 1 Performance comparison of prediction models

5 结束语

针对交通流数据含有噪声成分, 短时交通流预测精度不高的问题, 提出了基于奇异谱分析和组合核函数最小二乘支持向量机的短时交通预测模型(SSA-CKF-LSSVM)。运用奇异谱分析方法, 将交通流时间序列分解和重构, 消除了原序列的噪声成分。使用降噪后的交通流数据对组合核函数最小二乘支持向量机进行训练, 并通过PSO算法确定模型参数。以厦门市莲前西路的实测交通流数据为例, 验证了新建模型的预测效果并与其他3种模型的预测结果进行对比分析, 结果表明新建模型预测性能良好, 能够有效提高交通流预测精度。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	邴其春, 杨兆升, 周熙阳, 等. 基于向量误差修正模型的短时交通参数预测[J]. 吉林大学学报: 工学版, 2015, 45(4): 1076-1081. Bing Qi-chun, Yang Zhao-sheng, Zhou Xi-yang, et al. Short-term traffic parameters prediction method based on vector error correction model[J]. Journal of Jilin University(Engineering and Technology Edition), 2015, 45(4): 1076-1081. [本文引用:1]
[2]	van Lint J W C, Hoogendoorn S P, van Zuylen H J. Accurate freeway travel time prediction with state-space neural networks under missing data[J]. Transportation Research Part C: Emerging Technologies, 2005, 13(5): 347-369. [本文引用:1]
[3]	Stathopoulos A, Karlaftis M G. A multivariate state space approach for urban traffic flow modeling and prediction[J]. Transportation Research Part C: Emerging Technologies, 2003, 11(2): 121-135. [本文引用:1]
[4]	Sun H, Liu H, Xiao H, et al. Use of local linear regression model for short-term traffic forecasting[J]. Transportation Research Record: Journal of the Transportation Research Board, 2003, 1836: 143-150. [本文引用:1]
[5]	Chand ra S R, Al-Deek H. Predictions of freeway traffic speeds and volumes using vector autoregressive models[J]. Journal of Intelligent Transportation Systems, 2009, 13(2): 53-72. [本文引用:1]
[6]	Wang Y, Papageorgiou M. Real-time freeway traffic state estimation based on extended Kalman filter: a general approach[J]. Transportation Research Part B: Methodological, 2005, 39(2): 141-167. [本文引用:1]
[7]	龚勃文, 林赐云, 李静, 等. 基于核自组织映射-前馈神经网络的交通流短时预测[J]. 吉林大学学报: 工学版, 2011, 41(4): 938-942. Gong Bo-wen, Lin Ci-yun, Li Jing, et al. Short-time traffic flow prediction based on KSOM-BP neural network[J]. Journal of Jilin University(Engineering and Technology Edition), 2011, 41(4): 938-942. [本文引用:1]
[8]	Hong W C, Dong Y C, Zheng F F, et al. Forecasting urban traffic flow by SVR with continuous ACO[J]. Applied Mathematical Modelling, 2011, 35(3): 1282-1291. [本文引用:1]
[9]	Suykens J A K, van Gestel T, Brabanter D E. Least Squares Support Vector Machines[M]. Singapore: World Scientific, 2002. [本文引用:1]
[10]	Xiao Y, Liu J J, Hu Y, et al. A neuro-fuzzy combination model based on singular spectrum analysis for air transport demand forecasting[J]. Journal of Air Transport Management, 2014, 39: 1-11. [本文引用:1]
[11]	罗勇, 匡翠林, 卢辰龙, 等. 基于SSA的GPS坐标序列去噪及季节信号提取[J]. 大地测量与地球动力学, 2015, 35(3): 391-395. Luo Yong, Kuang Cui-lin, Lu Chen-long, et al. GPS coordinate series denoising and seasonal signal extraction based on SSA[J]. Journal of Geodesy and Geodynamics, 2015, 35(3): 391-395. [本文引用:1]
[12]	Smits G F, Jordan E M. Improved SVM regression using mixtures of kernels[C]∥Proceedings of the 2002 International Joint Conference, Honolulu, NJ, 2002: 2785-2790. [本文引用:1]

2015

0.0

. 2015, 45(4):1076-1081

Short-term traffic parameters prediction method based on vector error correction model

基于向量误差修正模型的短时交通参数预测

Bing Qi-chun , Yang Zhao-sheng , Zhou Xi-yang

邴其春, 杨兆升, 周熙阳

... 实时、准确的短时交通流预测能够直接应用于ITS子系统中^[1],如先进的交通管理系统(ATMS)和先进的出行者信息系统(ATIS) ...

2005

0.0

... 微观交通流模拟则考虑的是单车行为以及路网中车与车之间的相互作用^[2,3] ...

2003

0.0

... 微观交通流模拟则考虑的是单车行为以及路网中车与车之间的相互作用^[2,3] ...

2003

0.0

... 例如:局部线性回归模型、ARMA模型和Kalman滤波模型^[4,5,6] ...

2009

0.0

... 例如:局部线性回归模型、ARMA模型和Kalman滤波模型^[4,5,6] ...

2005

0.0

... 例如:局部线性回归模型、ARMA模型和Kalman滤波模型^[4,5,6] ...

2011

0.0

. 2011, 41(4):938-942

Short-time traffic flow prediction based on KSOM-BP neural network

基于核自组织映射-前馈神经网络的交通流短时预测

Gong Bo-wen , Lin Ci-yun , Li Jing

龚勃文, 林赐云, 李静

A short-term traffic flow prediction model was built based on KSOM-BP neural network. Using the kernel sample self-organizing map(KSOM) neural network, under the condition without a priori knowledge, the history samples with similar statistic character were classified into several categories by self-organizing and self-learning to enhance the statistic significance of the classified sample. A back-propagation(BP) neural network prediction model was built for the momentum-adaptive learning rate of every category sample to enhance the short-term traffic flow prediction accuracy, reduce the prediction time consumption. The model was validated using the practical road network data. The results show that the statistic index MARE of prediction error of KSOM-BP neural network is less than 7%, and less by 4% than that of BP network based on the whole sample without classification. The modeling time consumption of KSOM-BP neural network is also less than BP neural network without sample classification. All of this proves the validation and state-of-the-art of the proposed method.

提出了一种基于KSOM-BP神经网络的交通流短时预测模型。利用基于核函数的样本自组织映射神经网络(KSOM)，在没有任何先验知识的情况下，自组织、自学习地将具有相似统计特性的历史样本划分成一类，促使分类样本统计特性更集中显著。对每个类别的样本分别建立动量-自适应学习速率的BP神经网络预测模型，以期提高交通流短时预测精度，减少预测时间。结合实际城市道路数据对模型进行验证。验证结果表明：KSOM-BP神经网络的预测误差统计指标MARE小于7%，比基于全部样本训练的BP神经网络的MARE减少4%左右；同时，KSOM-BP神经网络建模时间更短，证明了本文方法的有效性和先进性。

... 例如人工神经网络和支持向量机^[7,8] ...

2011

0.0

... 例如人工神经网络和支持向量机^[7,8] ...

2002

0.0

... 最小二乘支持向量机(Least squares support vector machine,LSSVM)是支持向量机的一种改进形式,学习速度更快^[9] ...

2014

0.0

... 奇异谱分析(Singular spectrum analysis,SSA)是一种有效的降噪方法,已在水文预测、电力负荷预测和天气预测等方面有了相关应用^[10] ...

2015

0.0

. 2015, 35(3):391-395 DOI:doi:10.14075/j.jgg.2015.03.007

GPS coordinate series denoising and seasonal signal extraction based on SSA

基于SSA的GPS坐标序列去噪及季节信号提取

Luo Yong , Kuang Cui-lin , Lu Chen-long

罗勇, 匡翠林, 卢辰龙

Singular Spectrum Analysis (SSA) is one method of generalized power spectrum analysis and it is able to identify and enhance signal stability, especially the periodic signal. It therefore has good application in the time series analysis. GPS coordinate series analysis is currently a hot issue. This paper studies GPS coordinate time series denoising and seasonal signal extraction based on SSA. Through analysis of simulation experimental data and GPS measurement data, as well as comparison with empirical mode decomposition (EMD) and wavelet analysis, numerical results show that SSA, EMD and wavelet analysis are effective denoising methods, but that the SSA denoising performance is superior and can separate the cycle information from the GPS time series more effectively and stably.

基于SSA技术对GPS时序的去噪及季节信号分离进行研究。通过对模拟数据及GPS实测数据的分析，并与经验模式分解EMD（empirical mode decomposition）和小波分析方法进行对比，结果表明，SSA、EMD和小波分析均是有效的去噪方法，但SSA去噪性能更优越，且能更有效和稳定地从GPS时序中提取周期项信号。

... 文献^[11]使用多种方法处理GPS坐标数据,结果表明SSA降噪效果优于小波和经验模态分解方法 ...

2002

0.0

... 而全局核函数与之相反^[12] ...