路段直线式公交站点对公交车延误的影响

引用本文

梁士栋, 赵淑芝, 马明辉, 刘华胜, 卢春秀. 路段直线式公交站点对公交车延误的影响. 吉林大学学报:工学版, 2016, 46(6): 1807-1817
LIANG Shi-dong, ZHAO Shu-zhi, MA Ming-hui, LIU Hua-sheng, LU Chun-xiu. Impacts of linear bus stop on bus delays. Journal of Jilin University Engineering and Technology Edition, 2016, 46(6): 1807-1817 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201606008
Permissions

路段直线式公交站点对公交车延误的影响

梁士栋, 赵淑芝, 马明辉, 刘华胜, 卢春秀

吉林大学交通学院,长春 130022

作者简介:梁士栋(1990-),男,博士研究生.研究方向:交通运输规划.E-mail:liangsd14@mails.jlu.edu.cn

基金项目:国家自然科学基金项目(51378237)

摘要

针对在路段上设置直线式公交站点的公交车延误问题,根据公交站点设置在两相邻交叉口间路段位置的不同,将其划分为上游公交站点和下游公交站点两类,分别利用交通波理论分析交通流稳定输入下直线式公交站点对交通运行的影响,并构建交叉口处交通流变化反作用于公交车的延误计算模型。当公交站点设置在路段上游时,根据公交车通过交叉口情况不同,将公交车延误划分为3种情况,并根据每种情况发生的概率以及对应公交车延误计算得到公交车延误期望值。当公交站点设置在路段下游时,通过抽象坐标系描述交叉口车辆的运行轨迹,构建公交车延误模型,并利用Matlab编程实现对延误的计算。仿真结果表明:相比于未设置公交站点情况,当公交站点设置在路段上游时,公交车延误较小,且随着流量、周期以及停靠时间的增加,公交车延误逐渐增大;公交站点设置在路段下游时,随着公交站点与下游交叉口距离的增大,公交车延误呈先减小而后增大的趋势。

关键词: 交通运输系统工程; 公交车延误; 交通波理论; 信号交叉口; 公交站点位置

中图分类号:U491 文献标志码:A 文章编号:1671-5497(2016)06-1807-11

Impacts of linear bus stop on bus delays

LIANG Shi-dong, ZHAO Shu-zhi, MA Ming-hui, LIU Hua-sheng, LU Chun-xiu

College of Transportation, Jilin University, Changchun 130022,China

Abstract

In order to reduce the bus delays in a bus stop, which located near signalized intersection, the bus stops are classified into two categories according to their locations on the road. A bus delay model is established based on the shockwave theory by analysis of the interaction influence between bus stop and traffic flow. If the bus stop is located upstream the intersection, bus delays include three cases and the expected delay values are obtained by probabilities and corresponding delay case. If the bus stop is located downstream the intersection, the coordinate system is established to describe travelling track of both buses and cars, and the bus delay model is constructed. Simulation was carried out with aid of Matlab. Simulation results show that, with the growth of traffic flow, signal cycle and dwell time, the bus delay increases if the bus stop is located upstream the intersection. If the bust stop resides downstream the intersection, the bus delay decreases first and then increases as it approach the upstream stop.

Key words: engineering of communication and transportation system; bus delays; shockwave theory; signalized intersection; bus stop location

Show Figures

0 引言

在交叉口附近设置公交站点便于交叉口处两条垂直公交线路上乘客换乘, 能够有效提升公共交通换乘效率。交叉口处公交站点根据位置不同可分为路段上游公交站点和路段下游公交站点^[1]。由于当公交车在直线式公交站点停靠时, 需占用一定的道路资源而形成短暂道路瓶颈, 使得公交站点附近可供道路车辆行驶的车道数减少, 在一定程度上干扰了道路车辆的正常运行。同时, 受到影响的道路交通流会反作用于公交车的运行, 导致公交车延误变化。因此, 为了能够实现公交站点的合理布局, 为公交规划提供科学有效的理论支持, 有必要对设有直线式公交站点路段的公交车辆运行情况进行分析并构建合理的公交车延误计算模型。

根据公交车站点设置形式不同, 可将其划分为直线式公交站点^[2]和港湾式公交站点两类^[3], 一般认为公交车在港湾式公交站点停靠时, 公交车与道路车流处于分离状态, 停靠行为对道路车流影响较小, 而直线式公交站点处公交车停靠行为对道路车辆运行存在较大影响^[4]。

目前, 针对公交车延误影响分析的相关研究^{[5, 6, 7, 8]}主要考虑公交车在站点处的延误, 包括进站排队延误、服务延误、出站延误等, 公交车在交叉口处的延误则直接应用交叉口车辆延误计算公式进行计算^{[9, 10]}。然而公交车在公交站点停靠不仅对道路车辆运行产生影响, 也间接影响公交车自身在交叉口处的排队和释放过程。因此, 公交车延误不应直接采用已有信号交叉口车辆延误公式计算得到。同时, 公交站点在交叉口设置位置不同, 对道路车辆运行情况影响也存在一定的差异性^{[11, 12, 13]}。因此, 需在分析公交车延误影响因素的基础上, 根据公交站点位置不同, 分别对路段上游和下游设置公交站点时的公交车延误情况进行分析。再者, 由于信号交叉口已普遍存在于城市路网中, 其对交叉口附近车辆延误的影响不可忽视。同时, 公交车具有乘客运输量大的特点, 公交车在交叉口附近产生延误直接影响公交乘客的总体延误。因此, 有必要对信号配时参数、公交车在直线式公交站点处停靠时间以及公交站点与交叉口距离对公交车延误的影响进行系统分析。

综上, 本文在分析直线式公交站点(以下简称公交站点)对道路车辆运行影响的基础上, 利用交通波理论分别对路段上游和下游设置公交站点两种情况下公交车在交叉口上游路段的运行机理进行了分析。当路段上游设置公交站点时, 将公交车延误分为3种情况, 并根据每种情况发生的概率以及对应的公交车延误, 利用统计学方法计算得到公交车延误期望值; 当公交站点设置在路段下游时, 将公交车延误划分为9种情况, 并通过抽象坐标系描述交叉口车辆的运行轨迹, 分别构建公交车延误模型, 利用编程实现公交车延误的计算。

1 模型基础及假设条件

1.1 交通波理论

交通波理论源于交通流LWR(Light hill Whitham Richards)理论, 可被描述为在恒定道路交通流输入条件下, 存在两种不同密度的分界点连续向上游传播而产生的交通波^[14]。经典模型中交通波传播速度为:

$\begin{matrix} w = \frac{q_{1} - q_{2}}{ρ_{1} - ρ_{2}} = \frac{Δq}{Δρ} \end{matrix}$ (1)

式中:q₁、q₂为两种车流状态的流量; ρ ₁、ρ ₂为两种车流状态的密度。

本文对道路运行车辆延误模型进行构建, 其中车辆排队长度单位为veh。为了简化公式方便计算, 将波速量纲转换为veh/s, 且取值均为正数, 量纲转换后的波速仍然表示速度, 其物理意义为单位时间内交通波能够传播的距离。交通波的波速表示为:

$\begin{matrix} w = |ρ_{j} \cdot \frac{Δq}{Δρ}| \end{matrix}$ (2)

式中: $\begin{matrix} ρ_{j} \end{matrix}$ 为阻塞状态时的交通流密度。

1.2 假设条件

为了有效分析公交车在公交站点停靠对道路运行车辆延误的影响, 提升所构建模型实际应用的可靠性和可操作性, 构建车辆延误模型条件如下:①交通流处于较为稳定的非饱和状态; ②交叉口信号配时为固定配时; ③公交车呈离散状态到达, 不考虑多个公交车同时到达公交站点的情况。

1.3 公交站点位置分类

在本文的研究中, 路段下游公交站点是指靠近下游交叉口的公交站点; 路段上游公交站点是指远离下游交叉口的公交站点。两类公交站点根据站点与下游交叉口的距离和下游交叉口处的最大车辆排队长度具体区分。当下游交叉口最大排队长度大于公交站点与下游交叉口的距离, 即站点处公交车运行会受到下游交叉口处上溯的排队车辆影响, 该类站点在本文研究中定义为路段下游公交站点。反之, 当下游交叉口处的最大排队长度小于公交站点与下游交叉口的距离, 即下游交叉口处的排队车辆上溯不到公交站点位置, 该类站点在本文的研究中称为路段上游公交站点。

2 路段上游公交站点对公交车延误的影响

2.1 公交车延误建模

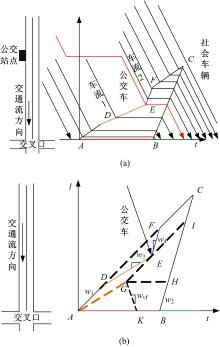
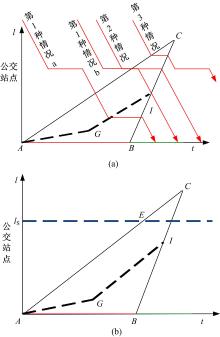
当公交车在路段上游公交站点停靠时, 公交站点上游输入流量为q_in, 受到公交车阻滞影响所形成的短暂瓶颈区域向下游输出流量为q_out。当公交车在公交站点停靠t_d时间后驶离时, 站点上游受阻滞车辆将以近似饱和流率驶过站点区域, 并进入下游路段。一个周期内, 在有公交车进入路段情况下, 受影响车辆在交叉口的累积和释放曲线如图1所示。图1(b)中, w₁为车辆不受公交车影响时到达交叉口时的停车波速; w₂为交叉口排队车辆启动波速; w₃为受公交车停靠影响的车辆到达交叉口的停车波速; w₄为随公交车到达交叉口的车辆的停车波速; w_vf为自由流速度转化为波速量纲之后的值; λ 为车道数。

	Figure Option View Download New Window
	图1 交叉口处受影响车辆到达和驶离过程Fig.1 Affected vehicles arriving and discharging process at intersection

图1(a)为路段上游设置公交站点时, 公交车以及社会车辆行驶的时空轨迹, 红色有向线段表示公交车的时空轨迹, 黑色的有向线段表示社会车辆的时空轨迹。图1(b)为路段上游设置公交站点时, 在公交车的影响下交叉口处的车辆交通波轨迹。图1中的横坐标为时间轴, AB为红灯时段, 纵坐标表示车辆与交叉口处停车线的距离; E点为公交车到达交叉口并加入车辆排队的时空点; AC为正常情况下车辆到达交叉口时产生的停车波; DE为公交车在公交站点停靠时, 受影响车流q_out流向路段下游到达交叉口时产生的停车波, 该部分车流定义为车流1, 由于公交车的阻滞作用车流1较正常车流q_in减小, 因此DE的斜率w₃比AC斜率w₁小; EF为随公交车到达交叉口的车辆在交叉口处产生的停车波, 由于公交车后方为受阻滞车辆, 近似以饱和流率随公交车向路段下游行驶, 因此当该部分车流(定义为车流2)到达交叉口时所产生的停车波EF的斜率w₄较大, 近似等于w₂。从整体角度考虑, 一个周期内, 无论受到公交车停靠影响与否, 到达交叉口的总体车辆数不变, 因此C点的时空位置不受影响, F点位于线段AC上。

结合图1对路段上游公交站点对公交车延误影响展开分析。公交车到达交叉口时刻具有随机性, 随着公交车到达时刻的推迟, 图1中DF沿着AC向右上方移动, 由于点D、E及F相对位置固定, 故三角形DEF大小及形状不变, 点E与AC的垂直距离始终为一恒定值, 因此公交车加入排队时空点E的集合GI与AC平行。相反, 当点A与D重合后, 随着公交车到达时刻的提前, 三角形DEF向左下方移动, 由于DE的斜率恒为w₃, 点A在DE上, 因此直观上DE过A点向左下方移动, 图1中公交车加入车辆排队时空点的集合AG与DE平行且相等。

综上所述, 公交车到达交叉口处加入车辆排队点E的所有时空点集合为折线AGI。G点的纵坐标值l_G为公交车在公交站点停靠t_d时段内车流1在交叉口排队时所占道路的长度, 表示为(q_out· t_d)/λ 。H点无具体物理意义, 为公交车延误计算所需的辅助点, GH与AB平行。根据图1中呈现的相对位置关系以及物理意义, 可以得到点G、点H和点I的坐标, 如式(3)所示:

$\begin{matrix} \{\begin{matrix} G (\frac{q_{out} t_{d}}{λ w_{3}}, \frac{q_{out} t_{d}}{λ}) \\ H (\frac{q_{out} t_{d}}{λ w_{2}} + t_{r}, \frac{q_{out} t_{d}}{λ}) \\ I (\frac{t_{G} w_{1} - t_{r} w_{2} - l_{G}}{w_{1} - w_{2}}, l_{G} + (t_{I} - t_{G}) w_{1}) \end{matrix} \end{matrix}$ (3)

当公交车到达交叉口加入车辆排队时空点位于A点时, 结合图1, 公交车排队延误数学抽象为对应AB线段长度值, 即为红灯时长t_r。当公交车到达交叉口加入车辆排队的时空点位于G点时, 对应的公交车排队延误为GH的横坐标长度值, 即G点和H点横坐标之差t_H-t_G; 当公交车到达交叉口加入车辆排队的时空点位于AG上时, 公交车排队延误则介于t_H-t_G和t_r之间。根据图1中的几何关系可知, 公交车平均排队延误为梯形ABGH内平行于AB和GH的所有线段平均值, 其数值为t_H-t_G和t_r的平均值, 可表示为:

$\begin{matrix} D_{1} = \frac{1}{2} (t_{H} - t_{G} + t_{r}) \end{matrix}$ (4)

公交车到达交叉口加入车辆排队的时空点位于AG上, 在一个周期内发生的概率为公交车到达停车线的时间范围除以周期时长。公交车到达停车线的时间范围为线段AG随公交行驶轨迹在横坐标轴上投影线段AK的长度, 表示为 $\begin{matrix} t_{D_{1}} \end{matrix}$ :

$\begin{matrix} t_{D_{1}} = \frac{l_{G}}{w_{vf}} + \frac{l_{G}}{w_{3}} \end{matrix}$ (5)

式中:l_G/w₃为G点的横坐标值; l_G/w_vf为G点沿公交车自由行驶的方向与横坐标轴的交点K和点G的横向时间距离。

那么在一个周期C内, 该情况出现的概率为P₁:

$\begin{matrix} P_{1} = \frac{t_{D_{1}}}{C} = \frac{l_{G} (w_{3} + w_{vf})}{C w_{3} w_{vf}} \end{matrix}$ (6)

当公交车到达交叉口车辆排队的时刻位置为点I时, 公交车恰好不用排队直接通过交叉口, 此时公交车排队延误为零; 当公交车到达交叉口加入车辆排队的时空点位于G点时, 对应的公交车排队延误为t_H-t_G。因此, 公交车到达交叉口并开始加入车辆排队的时空点位于线段GI上时, 公交车延误值介于零和t_H-t_G之间, 根据三角形的几何关系及图形所代表的物理意义, 此情况对应的公交车平均排队延误为线段GH横坐标长度的平均值, 可表示为:

$\begin{matrix} D_{2} = \frac{1}{2} (t_{H} - t_{G}) \end{matrix}$ (7)

此种情况发生的时刻分布在线段GI上, 随公交行驶轨迹线段GI在图1横坐标轴的投影长度为 $\begin{matrix} t_{D_{2}} \end{matrix}$ :

$\begin{matrix} t_{D_{2}} = t_{I} + \frac{l_{I}}{w_{vf}} - t_{D_{1}} \end{matrix}$ (8)

式中:t_I+ $\begin{matrix} \frac{l_{I}}{w_{vf}} \end{matrix}$ 为点I随公交车自由行驶方向与横坐标交点的横坐标值。

那么一个周期C内, 该种情况发生的概率为P₂:

$\begin{matrix} P_{2} = \frac{t_{D_{2}}}{C} = \frac{t_{I} w_{v f} - t_{D_{1}} w_{vf} + l_{I}}{C w_{vf}} \end{matrix}$ (9)

以上两种情况为公交车行驶至交叉口, 受交叉口车辆排队阻滞作用加入排队后驶离交叉口的情况。如公交车在绿灯时段到达交叉口, 并在下一个周期车辆排队开始前驶离交叉口, 则该种情况下公交车通过交叉口无需排队, 那么公交车在交叉口处的停车延误为0。此时, 公交车到达交叉口停车线的时间点集合为 $\begin{matrix} t_{D_{3}} \end{matrix}$ :

$\begin{matrix} t_{D_{3}} \end{matrix}$ =C-( $\begin{matrix} t_{D_{1}} \end{matrix}$ + $\begin{matrix} t_{D_{2}} \end{matrix}$ )=C-(t_I+ $\begin{matrix} \frac{l_{I}}{w_{vf}} \end{matrix}$ ) (10)

由于一个典型周期内仅有可能发生以上3种情况, 因此 $\begin{matrix} t_{D_{3}} \end{matrix}$ 为周期时长减去 $\begin{matrix} t_{D_{1}} \end{matrix}$ 和 $\begin{matrix} t_{D_{2}} \end{matrix}$ 。该情况的概率P₃为:

$\begin{matrix} P_{3} = \frac{t_{D_{3}}}{C} = 1 - \frac{w_{vf} t_{I} + l_{I}}{w_{vf} C} \end{matrix}$ (11)

2.2 公交车延误期望

本文所指的公交车延误为公交车实际通过交叉口停车线的时刻与自由到达并驶离停车线时刻之差。公交车延误受到公交车进入路段时刻的影响, 因此路段上游设置公交站点时, 公交车延误由延误的数学期望值表示。一个周期内根据公交车到达交叉口时段的不同将公交车延误分为3种情况, 每种情况的公交车平均延误及出现概率可由式(4)~式(11)获取, 根据数学期望的定义, 一辆公交车延误期望值等于每一种情况的延误与发生概率乘积之和。由于公交车需在公交站点停靠服务结束后驶入路段下游, 因此每一种情况的公交车平均延误计算应将停靠时间t_d考虑在内。综上, 当路段上游设置直线式公交站点时, 所对应的公交车延误D_upstream数学期望为:

D_upstream=P₁(D₁+t_d)+P₂(D₂+t_d)+

P₃(D₃+t_d)=D₁P₁+D₂P₂+

D₃P₃+(P₁+P₂+P₃)t_d=

D₁P₁+D₂P₂+D₃P₃+t_d (12)

3 路段下游公交站点对公交车延误的影响

3.1 公交车延误分析

相对于路段上游设置公交站点的情况, 路段下游公交站点与交叉口进口道距离较近, 公交站点对公交车延误影响更加复杂, 主要体现在下游公交站点处公交车停靠或驶离将受交叉口车辆排队干扰, 无法直接利用数学方法准确获取公交车延误期望, 因此通过应用计算机编程方法实现公交车延误期望的计算。

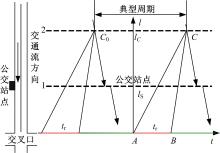
为了方便分析, 将公交车和道路车辆运行轨迹建立在同一坐标系下。实际情况中公交车到达公交站点时刻具有随机性, 但其在一个周期内的相对时刻可以在一个典型周期内表示, 图2中的C₀C即为本文选取的典型周期。图2中的横坐标为时间轴, 纵坐标表示车辆与停车线的距离, 虚线1为公交站点的位置, 虚线2为车辆排队最远点的位置。路段下游公交站点定义为交叉口处车辆排队能够上溯波及到的位置, 因此虚线1在虚线2下方。

	Figure Option View Download New Window
	图2 一个周期内公交车到达与驶离Fig.2 Bus arriving and leaving process at intersection

图2中的三角形表示红灯期间车辆排队情况, AB为交叉口红灯时长t_r, 点C和点C₀分别表示相邻两个周期内车辆排队最远点的时空位置, 则公交车到达系统的时空点位置在线段C₀C上, 即公交行驶轨迹与虚线2的交点。当公交车在线段C₀C左端点进入系统时, 图2中过C₀点的有向线段表示公交车的行驶轨迹, 公交车进入系统后, 先以自由流速度到达公交站点进行停靠服务, 服务结束后驶离公交站点。公交车延误为公交车在无站点设置情况下直接自由行驶至停车线的时刻t_free与有站点设置情况下公交车实际行驶至停车线的时刻之差。

设第i类, 第j种情况下, 公交车实际驶离交叉口时刻为t_case_i_,_j, 则对应公交车延误D_ij为:

$\begin{matrix} D_{ij} = t_{casei, j} - t_{free} \end{matrix}$ (13)

公交车以自由流速度直接通过停车线的时刻表示为:

$\begin{matrix} t_{free} = t_{int} + \frac{l_{C}}{w_{vf}} \end{matrix}$ (14)

式中:t_int为公交车进入系统的时刻, 即图2中公交车行驶至虚线2的时刻; l_C/w_vf为公交车以自由流速度行驶至停车线所需的时间。

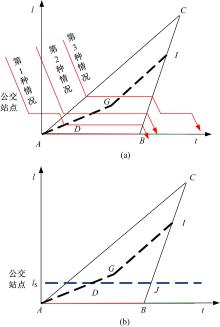
	Figure Option View Download New Window
	图3 第1类情况公交站点位置Fig.3 Bus stop location of case 1

图3(a)(b)中的横坐标为时间轴, 纵坐标表示与停车线的距离, 虚线l_S为公交站点的位置。图3中公交车进入系统并行驶至车辆排队位置时空点的集合为AGI, 与图1含义一致。根据公交站点与点A、I、G三点的位置关系不同, 可将公交车延误分析分为3类:第1类为公交站点处于点A和点G之间; 第2类为公交站点处于点I和点G之间; 第3类为公交站点处于点I和点C之间。

图3(a)为第1类情况下, 公交车可能出现的3种时空轨迹图。图3(b)表示公交站点的相对位置以及各个关键点示意图。第1类情况根据公交车到达和驶离公交站点时刻不同可分为3种情况。第1种情况物理含义为:公交车自由行驶至公交站点, 公交车停靠服务结束后的时空点位于D点左侧, 此时公交车自由驶离公交站点并加入交叉口处车辆排队, 公交车到达停车线并驶离交叉口的时刻为t_{case1, 1}:

$\begin{matrix} \begin{matrix} t_{case 1, 1} = t_{int} + t_{d} + \frac{l_{C}}{w_{vf}} + t_{r} + \\ \frac{(w_{3} - w_{2}) [l_{C} + w_{vf} (t_{int} + t_{d})]}{w_{2} (w_{vf} + w_{3})} (15) \end{matrix} \end{matrix}$

式中:t_r+ $\begin{matrix} \frac{(w_{3} - w_{2}) [l_{C} + w_{vf} (t_{int} + t_{d})]}{w_{2} (w_{vf} + w_{3})} \end{matrix}$ 为公交车加入受红灯阻滞车辆排队后排队等待时间, 该时间长度介于图3中AB代表的时间长度和DJ代表的时间长度之间。

t_int取值范围的左端点为典型周期C₀C的左端点C₀, 但如果典型周期较长或绿信比较大, 以致公交车从C₀点进入系统并完成停靠服务后直接在信号绿灯时段直接驶入交叉口, 并未产生停车延误时, 则不属于第1种情况。因此, t_int取值范围的左端点还应该考虑当公交车到达停车线时空位置为A时, 所对应的公交车进入系统的时刻, 即图2中公交车到达虚线2的时刻。t_int取值范围的右端点为当公交车到达交叉口停车线时空位置为D时所对应的公交车进入系统的时刻。

$\begin{matrix} \max (t_{C} - C, - \frac{l_{C}}{w_{vf}} - t_{d}) < t_{int} < \frac{l_{S}}{w_{3}} - t_{d} - \frac{l_{C} - l_{S}}{w_{vf}} \end{matrix}$ (16)

式中:t_C-C为图2中C₀点的横坐标值; -l_C/w_vf-t_d为公交车到达停车线时空位置为A时所对应的公交车进入系统的时刻, 即过点A沿公交车的逆向行驶轨迹与图2中的虚线2交点的横坐标; l_S/w₃-t_d-(l_C-l_S)/w_vf为当公交车到达停车线时空位置D时所对应的公交车进入系统的时刻。

第1类中第2种情况物理含义为:公交车自由行驶至公交站点, 且公交车在站点停靠期间, 排队车辆已上溯至公交站点处, 那么公交车驶离交叉口的时刻为公交车进入系统时刻、停靠时间以及自由行驶时间三者之和。如公交车停靠结束后由于道路车辆排队阻滞作用不能驶离公交站点, 即此时的公交车时空位置在D点右侧。如公交车服务结束后的时空点在J点左侧, 那么公交车服务结束后由于前方车辆排队阻滞作用, 致使公交车不能直接驶离公交站点, 而需等待排队释放时随排队车辆驶入下游。如公交车服务结束后的时空点在J点右侧, 那么公交车在服务结束之后自由驶离站点, 因此, 该部分的公交车延误可用max(0, t_r+l_S/w₂-t_int-(l_C-l_S)/w_vf-t_d)表示, 进而第1类中第2种情况下公交车到达停车线并驶离交叉口的时刻和t_int的取值范围如式(17)(18)所示:

$\begin{matrix} \begin{matrix} t_{case 1, 2} = t_{int} + t_{d} + \frac{l_{C}}{w_{vf}} + \max (0, t_{r} + \\ \frac{l_{S}}{w_{2}} - t_{int} - \frac{l_{C} - l_{S}}{w_{vf}} - t_{d}) (17) \\ \frac{l_{S}}{w_{3}} - t_{d} - \frac{l_{C} - l_{S}}{w_{vf}} < t_{int} < \frac{l_{S}}{w_{1}} - \frac{l_{C} - l_{S}}{w_{vf}} (18) \end{matrix} \end{matrix}$

第1类中第3种情况的物理含义为:公交车不能自由到达公交站点, 而是需先加入交叉口处的车辆排队等待, 然后随排队消散驶至公交站点进行停靠服务, 服务结束后驶离公交站点, 公交车行程时间为行驶时间、停靠时间和排队等待时间三者之和。因此, 公交车到达停车线并驶离交叉口的时刻和t_int的取值范围如式(19)(20)所示:

$\begin{matrix} \begin{matrix} t_{case 1, 3} = t_{int} + t_{d} + \frac{l_{C}}{w_{vf}} + t_{r} - \frac{t_{r} (l_{C} + t_{int} w_{vf})}{t_{C} (w_{1} + w_{vf})} (19) \\ \frac{l_{S}}{w_{1}} - \frac{l_{C} - l_{S}}{w_{vf}} < t_{int} < t_{C} (20) \end{matrix} \end{matrix}$

式中:t_r- $\begin{matrix} \frac{t_{r} (l_{C} + t_{int} w_{vf})}{t_{C} (w_{1} + w_{vf})} \end{matrix}$ 为公交车排队等待时间。

除上述3种情况外, 理论上还存在绿灯时间公交车自由到达站点, 服务结束后自由驶离交叉口情况(由于该情况较为简单, 因此该公交行驶的时空轨迹没有在图3中显示)。该情况公交车到达停车线并驶离交叉口时刻为t_{case1, 4}, 存在条件是t_int未出现在上述任何情况中。

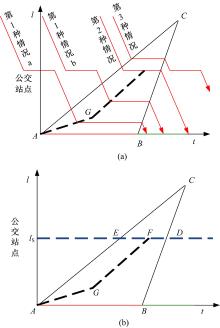
$\begin{matrix} t_{case 1, 4} = t_{int} + t_{d} + \frac{l_{C}}{w_{vf}} \end{matrix}$ (21)

图4(a)为第2类情况下, 公交车可能出现的时空轨迹图。图4(b)为公交站点相对位置以及各关键点位置示意图。根据图4(b)中点E、点D及点F的物理含义和几何位置可获取相应点坐标, 如式(22)所示:

$\begin{matrix} \{\begin{matrix} E (\frac{l_{S}}{w_{1}}, l_{S}) \\ D (t_{r} + \frac{l_{S}}{w_{2}}, l_{S}) \\ F (t_{G} + \frac{l_{S} - l_{G}}{w_{1}}, l_{S}) \end{matrix} \end{matrix}$ (22)

第2类中第1种情况的物理含义与第1类第1种情况相同, 但由于点A、G、F不在同一直线上因此需要分段考虑。公交车到达停车线并驶离交叉口的时刻为:

$\begin{matrix} \begin{matrix} t_{case 2, 1} = \\ \{\begin{matrix} t_{int} + t_{d} + \frac{l_{C}}{w_{vf}} + \frac{(t_{F} - t_{n}) (t_{H} - t_{G})}{t_{F} - t_{G}}, \\ if t_{n} > t_{G} \\ t_{int} + t_{d} + \frac{l_{C}}{w_{vf}} + \frac{l_{G}}{w_{2}} + t_{r} - t_{G} + \\ (t_{G} - \frac{l_{G}}{w_{2}}) \frac{t_{G} - t_{n'}}{t_{G}}, else \end{matrix} (23) \end{matrix} \end{matrix}$

式中:t_n= $\begin{matrix} \frac{l_{C} - l_{G} + t_{G} w_{1} + w_{vf} (t_{int} + t_{d})}{w_{vf} + w_{1}} \end{matrix}$ ; t_n'= $\begin{matrix} \frac{w_{vf} (t_{int} + t_{d}) + l_{C}}{w_{vf} + w_{3}} \end{matrix}$ 。

该情况t_int的取值范围为:

$\begin{matrix} \begin{matrix} \max (t_{C} - C, - \frac{l_{C}}{w_{vf}} - t_{d}) < t_{int} < \\ t_{F} - t_{d} - \frac{l_{C} - l_{S}}{w_{vf}} (24) \end{matrix} \end{matrix}$

第2类第2种情况物理含义与第1类第2种情况相同。公交车到达停车线并驶离交叉口的时刻公式表达形式与式(17)一致, t_int取值范围为:

$\begin{matrix} t_{F} - t_{d} - \frac{l_{C} - l_{S}}{w_{vf}} < t_{int} < t_{E} - \frac{l_{C} - l_{S}}{w_{vf}} \end{matrix}$ (25)

第2类中第3种情况的物理含义与第1类第3种情况相同。公交车到达停车线并驶离交叉口的时刻计算公式与式(19)一致, t_int的取值范围为:

$\begin{matrix} t_{E} - \frac{l_{C} - l_{S}}{w_{vf}} < t_{int} < t_{C} \end{matrix}$ (26)

第2类中第4种情况的物理含义则与第1类第4种情况一致, 且公交车到达停车线并驶离交叉口的时刻和t_int的取值范围表达与其相同。

	Figure Option View Download New Window
	图4 第2类情况公交站点位置Fig.4 Bus stop location of case 2

	Figure Option View Download New Window
	图5 第3类情况公交站点位置Fig.5 Bus stop location of case of case 3

图5(a)为第3类情况下, 公交车可能出现的时空轨迹图。图5(b)为公交站点相对位置以及各关键点位置示意图。第3类中第1种情况的物理含义为:公交车自由行驶至公交站点, 公交车停靠服务结束后自由驶离公交站点。如果公交车行驶位置在点I上方, 则公交车驶离公交站点后无需加入交叉口车辆排队直接驶离交叉口; 否则需要加入交叉口车辆排队等待, 并随排队消散。综上, 公交车到达停车线并驶离交叉口的时刻和t_int的取值范围如式(27)(28)所示:

$\begin{matrix} \begin{matrix} t_{case 3, 1} = \{\begin{matrix} t_{int} + \frac{l_{C}}{w_{vf}} + t_{d}, if t_{int} > t_{I} - t_{d} - \frac{l_{C} - l_{I}}{w_{vf}} \\ t_{int} + \frac{l_{C}}{w_{vf}} + t_{d} + \frac{(t_{I} - t_{x}) (t_{H} - t_{G})}{t_{I} - t_{G}}, else \end{matrix} (27) \\ \max (t_{C} - C, - \frac{l_{C}}{w_{vf}} - t_{d}) < t_{int} < t_{E} - t_{d} - \frac{l_{C} - l_{S}}{w_{vf}} (28) \end{matrix} \end{matrix}$

为了方便表达, 式(27)中未知参量t_x可表示为:

$\begin{matrix} t_{x} = \frac{(t_{int} + t_{d}) w_{vf} + t_{G} w_{1} + l_{C} - l_{G}}{w_{vf} + w_{1}} \end{matrix}$ (29)

第3类中第2种情况的物理含义与第1类第2种情况相同。公交车到达停车线并驶离交叉口的时刻计算公式与式(17)一致, t_int的取值范围为:

$\begin{matrix} t_{E} - t_{d} - \frac{l_{C} - l_{S}}{w_{vf}} < t_{int} < t_{E} - \frac{l_{C} - l_{S}}{w_{vf}} \end{matrix}$ (30)

第3类中第3种情况物理含义与第1类第3种情况相同。公交车到达停车线并驶离交叉口的时刻计算公式与式(19)一致, t_int的取值范围为:

$\begin{matrix} t_{E} - \frac{l_{C} - l_{S}}{w_{vf}} < t_{int} < t_{C} \end{matrix}$ (31)

以上针对公交车9种延误类型的分析仅考虑一个周期内的情况, 根据实际情况还应考虑公交车是否在下一个周期产生二次排队。如果公交车发生二次排队, 则需在上述公交车延误计算结果基础上加上二次排队产生的延误。

首先要判断是否出现了二次排队。如果公交车驶离交叉口的时刻大于信号周期结束时刻点C, 即t_case_i> C, 则公交车加入了下一周期的排队。

假设公交车与下一个周期的AG相交, 交点为M, 根据相对位置关系可得M点横坐标为:

$\begin{matrix} t_{M} = \frac{t_{casei, j} w_{vf} + t_{A'} w_{3}}{w_{vf} + w_{3}} \end{matrix}$ (32)

式中:A'为下一周期对应A的点。

若 t_M< t_G+C二次排队产生的延误为:

$\begin{matrix} D_{second, 1} = t_{GH} + \frac{t_{G^{'} M^{'}}}{t_{GA}} (t_{r} - t_{GH}) (33) \end{matrix}$

如果公交车与下一个周期的GI相交, 交点为Q, 根据相对位置关系可得Q点的横坐标为:

$\begin{matrix} t_{Q} = \frac{t_{casei} w_{vf} + t_{G} w_{1} - l_{G}}{w_{vf} + w_{1}} \end{matrix}$ (34)

若t_G+C< t_Q< t_I+C二次排队产生的延误为:

$\begin{matrix} D_{second, 2} = \frac{t_{I' Q}}{t_{IG}} t_{GH} \end{matrix}$ (35)

3.2 公交车延误计算步骤

由于路段下游设置公交站点对公交车延误影响的3类情况中每种情况延误出现概率不同, 因此, 不能将各种公交车延误直接取为平均值作为总体平均延误。为实现总平均延误计算的准确性, 本文选取公交车延误期望值作为总体平均延误计算方法。根据上文公交车延误分析可知, 公交车延误受交叉口处车辆排队影响较为复杂, 故本文借助计算机编程获取公交车延误的期望值。

基本思路为:首先令公交车到达系统的时空点为图2中的C₀点, 并判断所属情况, 进而计算对应的公交车延误, 然后公交车到达系统的时空点向右移动极小的时间间隔Δ t, 进一步判断属于哪种情况并计算对应的公交车延误, 依次类推, 公交车到达系统的时空点不断右移, 直到到达图2中C点, 计算所有公交车到达系统时空点所对应公交车延误的算术平均值, 该平均值就是公交车延误的近似期望延误值。本文所提出的公交车延误计算方法实施步骤如下:

(1)输入信号配时参数、站点位置、交通参数等基本参数值, 并计算波速值。

(2)初始化公交车到达系统的时间, 令公交车到达系统的时间为t_int=t_C-C。

(3)判断该公交车到达系统的时间所对应的公交车延误类型, 并计算得到公交车到达系统时刻t_int所对应的公交车延误, 公交车延误D_ij为公交车实际驶离交叉口的时刻t_case_i_,_j与自由驶离交叉口的时刻t_free之差, 如果公交车存在二次排队现象则需加上二次排队所需时间, D_ij=t_case_i_,_j-t_free+max{0, D_second}。

(4)公交车到达系统时间t_int右移一个极小时间间隔Δ t, t_int=t_int+Δ t, 并重复步骤(3), 直到公交车到达系统时间t_int到达图2中C点, 即t_int=t_C。

(5)计算公交车延误算术平均值D_downstream=[D(t_C-C)+D(t_C-C+Δ t)+…+D(t_C-Δ t)]Δ t/C。

根据以上步骤能够获得典型周期内每个时刻的公交车延误和公交车近似延误期望值D_downstream。

4 数值分析

采用一条双向四车道道路作为分析路段, 交叉口处信号配时为两相位, 以流率、信号周期、绿灯时间以及公交车停靠时间为输入变量, 分别对路段上游和下游设置公交站点时公交车延误进行数值分析。当参数不作为变量时, 基本参数设置如下:周期为120 s; 绿信比为0.5; 交通流量为1400 veh/h, 自由流速度为45 km/h; 阻塞密度为144 veh/(km· lane); 公交车在站点停靠时间取20 s。

4.1 路段上游设置公交站点时公交车延误

对路段上游设置公交站点的公交车延误进行数值计算, 得到公交车期望延误, 并分析流量、信号周期、绿信比及公交车在公交站点的停靠时间对公交车延误的影响。

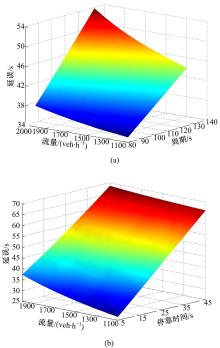
	Figure Option View Download New Window
	图6 公交车延误与流量的关系Fig.6 Relationship between bus delays and traffic flow

图6(a)为在信号周期和交通流量的共同作用下公交车延误的变化趋势, 公交车停靠时间为120 s, 绿信比为0.5。由图6(a)中三维曲面变化趋势可以看出, 随着流量的增加, 公交车延误呈上升趋势, 并且周期越大, 延误上升速率越快。

图6(b)为在公交车停靠时间和交通流量的共同作用下公交车延误的变化趋势。从图6(b)可知, 公交车停靠时间越长, 对应的公交车延误越大, 且随着流量的增加, 各停靠时间下所对应的公交车延误的增长幅度存在差异性, 在流量增加的条件下, 公交车停靠时间越长, 延误增加幅度越小。

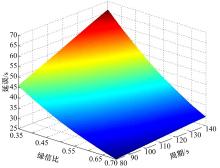
图7为在一定交通流条件下, 交叉口信号配时参数对公交车延误的影响。结合图7分析可知, 当交通流条件一定时(流量为1400 veh/h, 公交车停靠时间为20 s), 绿信比变化对于公交车延误的影响较为明显, 同一信号周期下, 公交车延误随绿信比的增大而减少, 其中延误变化幅度最大为39 s。当绿信比固定时, 随着周期的增大公交延误增加缓慢, 最大增幅为29 s。当周期和绿信比同时变化时, 公交延误变化较为显著。随着绿信比的减小, 周期的增大, 公交延误有加速上升的趋势。

	Figure Option View Download New Window
	图7 公交车延误与信号配时参数的关系Fig.7 Relationship between bus delays and signal timing parameters

4.2 路段下游设置公交站点时公交车延误

利用Matlab编程语言实现对路段下游设置公交站点时的公交车延误计算, 进而分析公交站点位置、交通流量以及周期对公交车延误的影响。为了提高计算结果的精确性, 公式中Δ t取值为0.01 s。

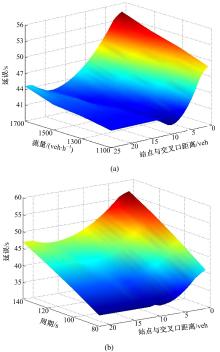
图8为公交车延误与公交站点位置关系, 从图8中曲面的变化趋势可知, 公交车延误随着公交站点与交叉口停车线距离的增加呈现先减小后增大的趋势, 最后增大到相同交通输入条件下公交站点设置在路段上游时公交车延误值。图8(a)为不同流量条件下, 公交车延误与公交站点位置关系。从图8(a)可以看出:不同流量输入条件下, 公交车延误随着公交站点与交叉口距离的增大呈波动变化, 且随着输入流量的减小, 公交站点位置与交叉口距离变化范围较小; 反之, 站点与交叉口距离变化范围较大。图8(b)为不同周期条件下, 公交车延误与公交站点位置关系。从图8(b)可知, 周期较长时, 对应的公交站点与停车线距离的变化范围较大, 反之亦然。

	Figure Option View Download New Window
	图8 公交车延误与站点位置的关系Fig.8 Relationship between bus delays and locations of bus stop

5 结束语

以交通波理论为基础, 分别对公交站点设置在路段上游和路段下游公交车延误影响情况进行分析。当公交站点设置在路段上游时, 根据公交车在交叉口前行驶轨迹不同, 将公交车延误划分为3种情况, 并根据每种情况发生概率以及对应公交车延误, 利用统计学方法计算得到公交车延误期望值。结果表明:随着流量、周期和公交车停靠时间增大和绿信比的减小, 公交车延误呈现上升趋势。因此, 为了减小公交车延误, 可以适当减小周期, 增加公交车行驶相位的绿灯时长, 或优化站点设置, 提高公交车在站点的服务效率。当公交站点设置在路段下游时, 将公交车延误计算分为3类9种情况, 通过构造公交车在交叉口的排队及释放过程曲线, 计算公交车实际通过交叉口停车线的时刻, 并以此为基础计算公交车延误时间。利用计算机语言实现模型计算, 并通过数值分析得到公交车延误与公交站点和交叉口距离关系。结果表明, 公交车延误随站点与交叉口距离的增加呈先减小后增加趋势。因此, 相对于公交站点设置在路段上游的情况, 公交站点设置在路段下游时, 能够通过合理布设站点位置有效降低公交车的延误。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Fitzpatrick K, Hall K, Perkinson D, et al. Guidelines for the location and design of bus stops[R]. Washington DC: National Academy Press, 1996. [本文引用:1]
[2]	孙锋, 王殿海, 马东方. 直线型公交停靠站通行能力计算方法[J]. 西南交通大学学报, 2013, 48(3): 546-552. Sun Feng, Wang Dian-hai, Ma Dong-fang. Method for computing on-line bus stop capacity[J]. Journal of Southwest Jiaotong University, 2013, 48(3): 546-552. [本文引用:1]
[3]	孙锋, 王殿海, 马东方, 等. 港湾式公交停靠站通行能力计算方法[J]. 东南大学学报: 英文版, 2012, 28(4): 485-489. Sun Feng, Wang Dian-hai, Ma Dong-fang, et al. Method for calculating the capacity of bus bay[J]. Journal of Southeast University (English Edition), 2012, 28(4): 485-489. [本文引用:1]
[4]	Furth P G, SanClemente J L. Near side, far side, uphill, downhill: impact of bus stop location on bus delay[J]. Transportation Research Record, 2006, 1971(1): 66-73. [本文引用:1]
[5]	Terry D S, Thomas G J. Farside bus stops are better[J]. Traffic Engineering, 1971, 41(3): 21-29. [本文引用:1]
[6]	Fitzpatrick K, Hall K, Perkinson D, et al. Location and design of bus stops[J]. ITE Journal, 1997, 67(5): 36-41. [本文引用:1]
[7]	Moura J L, Alonso B, Ibeas Á, et al. A two-stage urban bus stop location model[J]. Networks and Spatial Economics, 2012, 12(3): 403-420. [本文引用:1]
[8]	Gibson J. Effects of a downstream signalized junction on the capacity of a multiple berth bus-stop[C]∥Proceedings of the 24th PTRC European Transport Forum, London, 1996: 00737488. [本文引用:1]
[9]	Szeto W Y, Jiang Y, Wong K I, et al. Reliability-based stochastic transit assignment with capacity constraints: formulation and solution method[J]. Transportation Research Part C: Emerging Technologies, 2013, 35: 286-304. [本文引用:1]
[10]	Gu W, Li Y, Cassidy M J, et al. On the capacity of isolated, curbside bus stops[J]. Transportation Research Part B: Methodological, 2011, 45(4): 714-723. [本文引用:1]
[11]	Ibeas Á, dell'Olio L, Alonso B, et al. Optimizing bus stop spacing in urban areas[J]. Transportation Research Part E: Logistics and Transportation Review, 2010, 46(3): 446-458. [本文引用:1]
[12]	赵卓峰, 丁维龙, 李响. 面向交通感知数据处理业务的虚拟机调度系统[J]. 重庆邮电大学学报: 自然科学版, 2014, 26(6): 737-744. Zhao Zhuo-feng, Ding Wei-long, Li Liang. Virtual machine scheduling system for multiple traffic sensor data processing applications hosting[J]. Journal of Chongqing University of Posts and Telecommunications(Natural Science Edition), 2014, 26(6): 737-744. [本文引用:1]
[13]	张爱科, 符保龙. 基于最大收益平衡点动态变化的云资源调度算法[J]. 重庆邮电大学学报: 自然科学版, 2014, 26(5): 706-711. Zhang Ai-ke, Fu Bao-long. Cloud resource scheduling algorithm based on dynamic change of maximum profit equilibrium[J]. Journal of Chongqing University of Posts and Telecommunications(Natural Science Edition), 2014, 26(5): 706-711. [本文引用:1]

1996

0.0

... 交叉口处公交站点根据位置不同可分为路段上游公交站点和路段下游公交站点^[1] ...

2013

0.0

. 2013, 48(3):546-552 DOI:doi:10.3969/j.issn.0258-2724.2013.03.024

Method for computing on-line bus stop capacity

直线型公交停靠站通行能力计算方法

Sun Feng , Wang Dian-hai , Ma Dong-fang.

孙锋, 王殿海, 马东方

In order to improve the precision of calculation of bus stop capacity, the servicing process of buses at on-line stops was analyzed using the bus trajectories according to metropolitan bus operation status. On this basis, a method for computing on-line bus stop capacity was developed taking into account both the queue probability and the dwell time distribution. Then, the dwell time distribution function was fitted to the field-observed data of Hangzhou city; Kolmogorov-Smirnov (K-S) test shows that the log-normal distribution has the best goodness of fit, with the K-S value of two traffic periods being 0.083 9 and 0.050 6, respectively.The capacities of three kinds of bus stops were computed by MATLAB programming with different parameters of dwell time distribution. The results indicate that the capacity of bus stop with different berths decreases from 44.4% to 47.3% as the natural logarithmic mean of the dwell time μ increases. In addition, the capacity of bus stops was obtained by simulation using VISSIM software. The average relative error between the calculated and simulated results is 6.5%.

为了提高公交停靠站通行能力计算方法的精确性,针对目前城市的公交运行现状,使用时空分布图分析了公交车在直线式停靠站的服务过程,在此基础上,综合考虑停靠站排队概率和停靠时间分布,推导了公交停靠站通行能力计算模型.对杭州市公交车停靠时间的分布函数进行了拟合,对数正态分布的拟合程度最优, 2个交通时段的K-S检验值分别为0.083 9和0.050 6.用MATLAB编程得到不同分布参数下的通行能力结果表明:随着停靠时间对数平均值 μ 的增加,不同泊位数停靠站的通行能力减少了44.4%~47.3%;通过VISSIM仿真得到了停靠站的通行能力,模型计算值与仿真结果的平均误差为6.5%.

... 根据公交车站点设置形式不同,可将其划分为直线式公交站点^[2]和港湾式公交站点两类^[3],一般认为公交车在港湾式公交站点停靠时,公交车与道路车流处于分离状态,停靠行为对道路车流影响较小,而直线式公交站点处公交车停靠行为对道路车辆运行存在较大影响^[4] ...

2012

0.0

. 2012, 28(4):485-489 DOI:doi:10.3969/j.issn.1003-7985.2012.04.020

Method for calculating the capacity of bus bay

港湾式公交停靠站通行能力计算方法

Sun Feng , Wang Dian-hai , Ma Dong-fang

孙锋, 王殿海, 马东方

针对目前城市的公交运行现状,使用时空分布图分析了港湾式公交停靠站的车辆运行特性,并在此基础上建立了公交停靠站通行能力计算模型,该模型综合考虑了站点排队概率、停靠时间分布和汇入间隙的等待时间.利用杭州市的调查数据对公交车辆的站点停靠时间进行了分布拟合,结果表明对数正态分布的拟合效果最优.使用Matlab编程求出了不同停靠时间分布参数和外侧车道流量下的站点通行能力,结果显示随着分布参数和外侧车道流量的变化,站点通行能力的变化范围较大.最后,使用实测和仿真方法对模型进行了验证,模型计算值与实测数据、仿真数据的平均相对误差分别为8.78%和5.28%.

2006

0.0

1971

0.0

... 目前,针对公交车延误影响分析的相关研究^[5,6,7,8]主要考虑公交车在站点处的延误,包括进站排队延误、服务延误、出站延误等,公交车在交叉口处的延误则直接应用交叉口车辆延误计算公式进行计算^[9,10] ...

1997

0.0

2012

0.0

1996

0.0

2013

0.0

2011

0.0

2010

0.0

... 同时,公交站点在交叉口设置位置不同,对道路车辆运行情况影响也存在一定的差异性^[11,12,13] ...

2014

0.0

. 2014, 26(6):737-744 DOI:doi:10.3979/j.issn.1673-825X.2014.06.002

Virtual machine scheduling system for multiple traffic sensor data processing applications hosting

面向交通感知数据处理业务的虚拟机调度系统

Zhao Zhuo-feng , Ding Wei-long , Li Liang.

赵卓峰, 丁维龙, 李响

海量、实时、持续、多样的交通感知数据对承载其处理业务的IT设施提出了更高的要求,但现有云基础设施服务中采用的虚拟机调度方案在承载交通感知数据多处理业务时,会出现负载倾斜、负载不均及资源利用率不高的问题.为此,提出一种对交通感知数据处理业务敏感的虚拟机调度策略并设计了相应的调度算法,给出了系统的设计与实现,该系统可以适应计算密集和数据密集不同特征交通处理业务的承载,同时能够实现能耗约束下的负载平衡调度.通过基于实际交通应用场景的实验表明,该系统可在保障所承载业务的前提下实现虚拟机的负载均衡和优化节能.

... 同时,公交站点在交叉口设置位置不同,对道路车辆运行情况影响也存在一定的差异性^[11,12,13] ...

2014

0.0

. 2014, 26(5):706-711 DOI:doi:10.3979/j.issn.1673-825X.2014.05.024

Cloud resource scheduling algorithm based on dynamic change of maximum profit equilibrium

基于最大收益平衡点动态变化的云资源调度算法

Zhang Ai-ke , Fu Bao-long.

张爱科, 符保龙

云计算中资源调度是云计算高效利用的核心问题,主要研究如何对云端的资源进行有效地管理和调度.以从服务商需求的角度构建云资源调度的方法为切入点,从服务商的角度出发,在不损害用户和生产商利益的前提下,介入收益、成本、边际收益、边际成本等因素,以节省资源并获得服务商的最大收益为优化目的,根据最大收益平衡点随着负载变化的动态变化,构建了一种基于动态平衡点动态变化的云资源调度算法.通过比较当前周期和上一周期的边际收益变化,动态更新最大收益平衡点的位置,根据此位置对应的参数完成云资源调度.通过 CloudSim平台下的仿真实验表明,该方法比基于服务驱动的调度方法具有更快的响应、使用更少的虚拟机、能获得更大的收益.

... 同时,公交站点在交叉口设置位置不同,对道路车辆运行情况影响也存在一定的差异性^[11,12,13] ...