行人斜穿信号交叉口绿波设计及延误模型

引用本文

卢凯, 胡建伟, 李福樑, 张孜, 徐建闽. 行人斜穿信号交叉口绿波设计及延误模型. 吉林大学学报:工学版, 2016, 46(6): 1818-1826
LU Kai, HU Jian-wei, LI Fu-liang, ZHANG Zi, XU Jian-min. Green wave design and delay model of pedestrian diagonal crossing at signal intersetion. Journal of Jilin University Engineering and Technology Edition, 2016, 46(6): 1818-1826 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201606009
Permissions

行人斜穿信号交叉口绿波设计及延误模型

卢凯^1,², 胡建伟¹, 李福樑¹, 张孜³, 徐建闽^1,²

1.华南理工大学土木与交通学院,广州 510640

2.现代城市交通技术江苏高校协同创新中心, 南京 210096

3.广州市交通委员会,广州 510620

作者简介:卢凯(1979-),男,副教授,博士.研究方向:交通信号控制.E-mail:kailu@scut.edu.cn

基金项目:国家自然科学基金项目(61203164,61174184); 广州市珠江科技新星专项项目(2013J2200066); 广东省交通运输厅科技项目(2013-02-055); 广州市南沙区科技计划项目(2014MS11)

摘要

针对行人斜穿信号交叉口的实际过街需求,利用时距图分析了不同信号相位相序设置和行人过街组织方案的运行效果,提出了行人连续横穿信号交叉口的绿波带设计方式。根据行人到达和离开位置点的时刻线,推导了行人沿顺时针、逆时针以及不固定方向连续过街的延误模型,建立了总的行人连续过街延误模型通式。算例分析和仿真试验结果表明:本文提出的行人连续过街延误模型能够准确计算行人斜穿信号交叉口的延误时间,获取最佳的信号相位相序和行人过街组织方案,从而实现了行人连续过街的绿波通行,减少了行人连续过街的延误时间。

关键词: 交通运输系统工程; 行人斜穿; 行人绿波; 时距图; 延误模型; 信号相序

中图分类号:U491.5 文献标志码:A 文章编号:1671-5497(2016)06-1818-09

Green wave design and delay model of pedestrian diagonal crossing at signal intersetion

LU Kai^1,², HU Jian-wei¹, LI Fu-liang¹, ZHANG Zi³, XU Jian-min^1,²

1.School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510640, China

2.Jiangsu Province Collaborative Innovation Center of Modern Urban Traffic Technologies,Nanjing 210096,China

3.Communications Commission of Guangzhou Municipality, Guangzhou 510620, China

Abstract

Considering the real demand for pedestrian diagonal crossing at signal intersection, the operation effects of different signal phase settings and pedestrian crossing organization schemes were analyzed using the time-space diagram. Then, a design approach of pedestrian green wave for continuously crossing signalized intersection was proposed. According to the pedestrian arrival and departure time, the delay model of pedestrian continuous crossing along the clockwise, counterclockwise and unfixed directions were deduced. Finally, the general delay model for pedestrian continuous crossing was established. The results of case study and simulation show that the general delay model can predict the delay of pedestrian diagonal crossing accurately. This model can also help to acquire the best signal phase sequence and pedestrian crossing organization scheme. Therefore, the green wave can be obtained and the delay of the pedestrian diagonal crossing can be reduced.

Key words: engineering of communications and transportation system; pedestrian diagonal crossing; pedestrian green wave; time-space diagram; delay model; signal phase sequence

Show Figures

0 引言

由于受到城市功能区域及基础设施布局(例如在交叉口两端呈对角分布的公交站和写字楼、居民住宅区和商场超市、对向公交站台)等因素影响, 可能会产生一定量的行人斜穿信号交叉口的实际过街需求。对此, 可以利用直角人行横道, 通过设置两个相应的信号相位, 满足行人的斜穿需要; 也可以设置对角人行横道, 使用一个独立的行人相位, 直接满足行人的斜穿需要。相比而言, 设置对角人行横道可以减少行人过街的行走距离, 缩短行人过街时间, 一次性完成行人的斜穿过程, 但需要设置独立的行人相位, 且相位时间要求较长, 从而将加大交叉口的信号周期, 增加机动车辆的延误时间, 该方法主要适用于面积较小、车流量不大、行人流量较大的信号交叉口; 而直角人行横道适用范围更广、灵活性更高, 可适用于绝大部分的交叉口, 但其施划位置及信号相位应根据行人过街需求分布进行合理设置^[1], 以避免行人因为过街等待时间过长而选择违章过街^[2]。因此, 如何针对行人斜穿信号交叉口的实际过街需求, 研究交叉口的行人过街方案和信号相位设计具有重要意义。

针对行人过街延误国内外学者开展了广泛研究。Golani等^[3]综合考虑行人的起步时间、步行速度、行人间距等影响因素, 建立了高占用率人行横道的行人通行时间估算模型。Alhajyaseen等^[4]提出了一种针对不同行人需求组合和预定服务水平的人行横道宽度估算方法。Goldschmidt^[5]对行人过街延误与交通布局特点之间的关系展开研究, 分析了交通流量、道路宽度、信号配时、人群组成等因素对行人过街延误的影响。Virkler^[6]考虑行人过街的行为心理对信号交叉口的行人延误公式进行了修正。美国的通行能力手册^[7]和日本的交通信号控制手册^[8]都建立了相应的行人过街时间计算公式。冯树民等^{[9, 10]}研究了无干扰情况下的信号交叉口行人过街平均延误计算方法, 建立了考虑行人过街的交叉口信号配时优化模型。高利平^[11]分析了不同行人过街方式下的信号交叉口行人过街延误情况, 建立了信号交叉口基于过街方式的行人延误模型。钱大琳等^[12]针对道路等级相差较大的两相位信号交叉口, 建立了基于行人专用相位的行人过街延误计算模型和交叉口信号配时优化模型。马万经等^[13]研究了行人相位与机动车相位的组合设置问题, 提出了多相位信号控制交叉口行人相位的设计方法。赵韩涛等^[14]推导了行人过街时间函数, 建立了具有行人专用相位的过街时间模型。孙迪^[15]针对过街双向行人之间互相干扰的特点, 建立了对向行人干扰情况下的过街延误模型。然而, 目前关于行人连续横穿信号交叉口的优化设计和延误分析很少, 也鲜有如何结合信号交叉口的相位相序和行人过街组织形式进行一体化设计的相关理论研究。

对此, 本文针对行人斜穿信号交叉口的过街需求, 引入时距图分析方法, 提出行人斜穿信号交叉口的绿波带设计理念, 并利用行人到达和离开人行横道的时刻线, 推导行人连续横穿信号交叉口的过街延误模型, 为信号交叉口的行人连续过街设计和引导策略制定提供了理论依据。

1 行人连续过街绿波分析

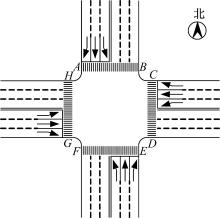
以图1所示的一个几何对称交叉口为例, 假设位置点A、B、C、D、E、F、G、H分别为北、东、南、西4个进口的人行横道起止点, 交叉口各进口均采用一次过街方式进行行人交通组织和相位设计(行人和机动车合用信号相位), 右转车流避让过街行人或者通过信号控制与相关行人通行相位分离。

	Figure Option View Download New Window
	图1 交叉口行人过街位置Fig.1 Positions of pedestrian crossing at intersection

为了便于理解和分析行人连续过街的绿波设计, 在此先假设该交叉口采用进口单独放行方式。当该交叉口采用顺时针的进口单独放行相位设计, 即信号相序为东进口机动车/北方行人相位→ 南进口机动车/东方行人相位→ 西进口机动车/南方行人相位→ 北进口机动车/西方行人相位(简称东南西北), 所有需要斜穿信号交叉口的行人, 例如从位置点A(H)到D(E)、从位置点C(B)到F(G)、从位置点E(D)到H(A)、从位置点G(F)到B(C), 按顺时针方向行走均可实现绿波通行, 其通行时间为T₁, 而按逆时针方向行走则无法实现绿波通行, 其通行时间为T₂(T₂远大于T₁), 如图2所示。

同样, 当该交叉口采用逆时针的进口单独放行相位设计, 所有需要斜穿信号交叉口的行人按逆时针方向行走均可实现绿波通行, 而按顺时针方向行走则无法实现绿波通行。

当以A(H)→ D(E)方向的行人过街需求为主时, 该交叉口的最佳相位相序设置为东南北西, 此时可为A(H)→ D(E)方向的过街行人在顺时针(A→ D)和逆时针(H→ E)两个方向上各形成一条行人绿波带, 其通行时间T₁与T₂近似相等且较小, 而对于其他方向(例如E(D)→ H(A)方向)的行人连续过街需求, 过街行人在顺时针(E→ H)和逆时针(D→ A)两个方向上均无法实现绿波通行, 其通行时间T₃与T₄近似相等且较大(T₃和T₄远大于T₁和T₂), 如图3所示。

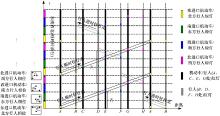	Figure Option View Download New Window
	图2 顺时针单放情况下的行人绿波带设计Fig.2 Design of pedestrian green wave in the case of one-phase-one-approach clockwise

	Figure Option View Download New Window
	图3 满足A(H)→ D(E)方向行人过街需求的行人绿波带设计Fig.3 Design of pedestrian green wave to meet the pedestrian crossing demand from A(H)to D(E)

同理, 当以E(D)→ H(A)方向的行人过街需求为主时, 该交叉口的最佳相位相序设置为南东西北, 此时可为E(D)→ H(A)方向的过街行人在顺时针(E→ H)和逆时针(D→ A)两个方向上各形成一条行人绿波带, 而对于其他方向(例如A(H)→ D(E)方向)的行人连续过街需求, 过街行人在顺时针(A→ D)和逆时针(H→ E)两个方向上均无法实现绿波通行。因此, 根据行人斜穿信号交叉口的交通需求, 可以利用行人时距图确定交叉口的最佳信号相位相序设置和行人过街组织方案, 实现行人连续横穿信号交叉口的绿波带设计。但由于交叉口的信号相位设计通常需要考虑进口道机动车放行以及干道车队协调控制^[16]的要求, 且行人在交叉口处总的延误时间还应包括其第一次过街前的等待时间, 因此需要进一步建立行人连续过街的延误模型, 以便于量化分析不同信号相位相序设置和行人过街组织方案的优劣。

2 行人连续过街延误模型

2.1 延误模型分析

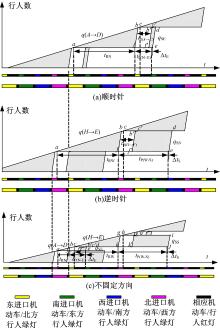
仍以图1所示的交叉口渠化为例, 假设该交叉口采用顺时针的进口单独放行相位设计, 针对由位置点A(H)至位置点D(E)的行人过街需求, 分析行人沿顺时针、逆时针以及不固定方向(根据先放行方向选择绕行方向)过街时的延误情况, 如图4所示。

为了避免过街行人与下一相位机动车辆发生冲突, 行人从位置点A(H)到位置点B(G)的步行时间t₀₍_A_→_B₎(t₀₍_H_→_G₎)与北(西)进口的行人绿灯时间t_GN(t_GW)和行人通行相位时间t_PN(t_PW)应满足t_PN≥ t₀₍_A_→_B₎+t_GN(t_PW≥ t₀₍_H_→_G₎+t_GW)。

假设A(H)→ D(E)方向连续过街行人达到率为q₍_A_→_D₎(q₍_H_→_E₎), q₍_A_→_D₎=q₍_H_→_E₎, 信号周期时长为C, 交叉口行人驻足区面积较小, 连续过街行人能够在相位时间t_PN(t_PW)内从位置点A(H)步行至位置点C(F), 即t_PN≥ t₀₍_A_→_B₎+t₀₍_B_→_C₎=t₀₍_A_→_C₎(t_PW≥ t₀₍_H_→_F₎)。以图4中的第2个信号周期为例, 分析不同行走方向下的行人延误情况如下所示。

	Figure Option View Download New Window
	图4 行人连续过街延误分析Fig.4 Delay analysis of pedestrian continuous crossing

(1)顺时针方向

在图4(a)中, 直线段abc表示行人到达位置点A的时刻; 折线段fbc表示行人离开位置点A走向位置点B的时刻; 折线段f'b'c'表示行人到达位置点C的时刻; 直线段ed表示行人离开位置点C走向位置点D的时刻; 三角形abf中的水平线段长表示行人在北进口等待绿灯的延误时间d_N; 多边形fbcc'b'f'中的水平线段长表示行人从位置点A到位置点C的步行时间t₀₍_A_→_C₎; 多边形f'b'c'de中的水平线段长表示行人在东进口等待绿灯的延误时间d_E; 梯形acde中的水平线段长表示行人从到达位置点A到离开位置C的时间差, 等于其步行时间t₀₍_A_→_C₎与延误时间d_N、d_E之和; 三角形abf的面积为行人在北进口等待绿灯的总延误时间; 多边形f'b'c'de的面积为行人在东进口等待绿灯的总延误时间, 两块阴影面积之和为行人顺时针过街的总延误时间D_(N-E); t_RN为北进口的累积行人红灯时间, t_RN=C-t_GN; t_P(N-E)为北进口与东进口的行人绿灯启亮时间差, t_P(N-E)=t_PN; Δ t_E为东进口的初始行人清空时间; q_SE为东进口人行横道的最大通行能力。

计算行人顺时针过街的总延误时间D_(N-E), 如式(1)所示:

$\begin{matrix} \begin{matrix} D_{(N - E)} = \frac{1}{2} [\frac{}{} (t_{RN} + t_{P (N - E)} + Δ t_{E}) + \\ (t_{RN} + t_{P (N - E)} + Δ t_{E} + \frac{q_{(A \to D)} C}{q_{SE}} - C)] \cdot \\ (q_{(A \to D)} C) - t_{0 (A \to C)} (q_{(A \to D)} C) = \\ [t_{RN} + t_{P (N - E)} + Δ t_{E} - \frac{C}{2} (1 - \frac{q_{(A \to D)}}{q_{SE}}) - \\ \frac{}{} t_{0 (A \to C)}] (q_{(A \to D)} C) \end{matrix} \end{matrix}$ (1)

得到行人顺时针过街的平均延误时间 $\begin{matrix} {\bar{d}}_{(N - E)} \end{matrix}$ 为:

$\begin{matrix} \begin{matrix} {\bar{d}}_{(N - E)} = \frac{D_{(N - E)}}{q_{(A \to D)} C} = t_{RN} + t_{P (N - E)} + \\ Δ t_{E} - \frac{C}{2} (1 - \frac{q_{(A \to D)}}{q_{SE}}) - t_{0 (A \to C)} (2) \end{matrix} \end{matrix}$

(2)逆时针方向

在图4(b)中, 直线段abc表示行人到达位置点H的时刻; 折线段fbc表示行人离开位置点H走向位置点G的时刻; 折线段f'b'c'表示行人到达位置点F的时刻; 直线段ed表示行人离开位置点F走向位置点E的时刻; 三角形abf中的水平线段长表示行人在西进口等待绿灯的延误时间d_W; 多边形fbcc'b'f'中的水平线段长表示行人从位置点H到位置点F的步行时间t₀₍_H_→_F₎; 多边形f'b'c'de中的水平线段长表示行人在南进口等待绿灯的延误时间d_S; 梯形acde中的水平线段长表示行人从到达位置点H到离开位置点F的时间差, 等于其步行时间t₀₍_H_→_F₎与延误时间d_W、d_S之和; 三角形abf的面积为行人在西进口等待绿灯的总延误时间; 多边形f'b'c'de的面积为行人在南进口等待绿灯的总延误时间, 两块阴影面积之和为行人逆时针过街的总延误时间D_(W-S); t_RW为西进口的累积行人红灯时间, t_RW=C-t_GW; t_P(W-S)为西进口与南进口的行人绿灯启亮时间差; t_P(W-S)=t_PW+t_PN+t_PE; Δ t_S为南进口的初始行人清空时间; q_SS为南进口人行横道的最大通行能力。

计算行人逆时针过街的总延误时间D_(W-S), 如式(3)所示:

$\begin{matrix} \begin{matrix} D_{(W - S)} = \frac{1}{2} [\frac{}{} (t_{RW} + t_{P (W - S)} + Δ t_{S}) + \\ (t_{RW} + t_{P (W - S)} + Δ t_{S} + \frac{q_{(H \to E)} C}{q_{SS}} - C)] \cdot \\ (q_{(H \to E)} C) - t_{0 (H \to F)} (q_{(H \to E)} C) = \\ [t_{RW} + t_{P (W - S)} + Δ t_{S} - \frac{C}{2} (1 - \frac{q_{(H \to E)}}{q_{SS}}) - \\ \frac{}{} t_{0 (H \to F)}] (q_{(H \to E)} C) \end{matrix} \end{matrix}$ (3)

得到行人逆时针过街的平均延误时间 $\begin{matrix} {\bar{d}}_{(W - S)} \end{matrix}$ 为:

$\begin{matrix} \begin{matrix} {\bar{d}}_{(W - S)} = \frac{D_{(W - S)}}{q_{(H \to E)} C} = t_{RW} + t_{P (W - S)} + \\ Δ t_{S} - \frac{C}{2} (1 - \frac{q_{(H \to E)}}{q_{SS}}) - t_{0 (H \to F)} (4) \end{matrix} \end{matrix}$

(3)不固定方向

行人将选择最近的行人通行相位完成第一次过街, 随后等待第二次过街通行相位完成穿越, 此时过街行人将分成两部分, 分别沿顺时针和逆时针两个方向过街。与情形(1)(2)类似, 在图4(c)中, 直线段abc表示沿北进口顺时针过街行人到达位置点A的时刻; 直线段cgh表示沿西进口逆时针过街行人到达位置点H的时刻; 直线段ed表示行人离开位置点C走向位置点D的时刻; 直线段ji表示行人离开位置点F走向位置点E的时刻; 三角形abf与多边形f'b'c'de的面积之和为行人顺时针过街的总延误时间D_(N-E); 三角形cgk与多边形k'g'h'ij的面积之和为行人逆时针过街的总延误时间D_(W-S); t_RN为北进口的累积行人红灯时间, t_RN=t_P(W-N)-t_GW; t_RW为西进口的累积行人红灯时间, t_RW=t_P(N-W)-t_GN; t_N为北进口的累积行人时间, t_N=t_RN+t_GN; t_W为西进口的累积行人时间, t_W=t_RW+t_GW。

计算行人顺时针过街的总延误时间D_(N-E), 如式(5)所示; 计算行人逆时针过街的总延误时间D_(W-S), 如式(6)所示:

$\begin{matrix} \begin{matrix} D_{(N - E)} = \frac{1}{2} [\frac{}{} (t_{RN} + t_{P (N - E)} + Δ t_{E}) + \\ (t_{RN} + t_{P (N - E)} + Δ t_{E} + \frac{q_{(A \to D)} t_{N}}{q_{SE}} - t_{N})] \cdot \\ (q_{(A \to D)} t_{N}) - t_{0 (A \to C)} (q_{(A \to D)} t_{N}) = \\ [t_{RN} + t_{P (N - E)} + Δ t_{E} - \frac{t_{N}}{2} (1 - \frac{q_{(A \to D)}}{q_{SE}}) - \\ \frac{}{} t_{0 (A \to C)}] (q_{(A \to D)} t_{N}) (5) \\ D_{(W - S)} = \frac{1}{2} [\frac{}{} (t_{RW} + t_{P (W - S)} + Δ t_{S}) + \\ (t_{RW} + t_{P (W - S)} + Δ t_{S} + \frac{q_{(H \to E)} t_{W}}{q_{SS}} - t_{W})] \cdot \\ (q_{(H \to E)} t_{W}) - t_{0 (H \to F)} (q_{(H \to E)} t_{W}) = \\ [t_{RW} + t_{P (W - S)} + Δ t_{S} - \frac{t_{W}}{2} (1 - \frac{q_{(H \to E)}}{q_{SS}}) - \\ \frac{}{} t_{0 (H \to F)}] (q_{(H \to E)} t_{W}) \end{matrix} \end{matrix}$ (6)

得到行人不固定方向过街的平均延误时间 $\begin{matrix} \bar{d} \end{matrix}$ , 如式(7)所示:

$\begin{matrix} \bar{d} = \frac{D_{(N - E)} + D_{(W - S)}}{q_{(A \to D)} t_{N} + q_{(H \to E)} t_{W}} \end{matrix}$ (7)

事实上, 情形(1)可以看作情形(3)的一种特例, 此时由于行人不会沿西进口逆时针过街, 因此, t_P(W-N)=C, t_GW=t_GN, t_RN=C-t_GN, t_N=C, t_W=0, D_(W-S)=0, 式(5)与式(1)等价, 式(7)与式(2)等价。情形(2)可以看作情形(3)的另一种特例, 此时由于行人不会沿北进口顺时针过街, 因此, t_P(N-W)=C, t_GN=t_GW, t_RW=C-t_GW, t_W=C, t_N=0, D_(N-E)=0, 式(6)与式(3)等价, 式(7)与式(4)等价。

2.2 延误模型通式

根据以上分析, 建立行人从位置区域i到位置区域j的延误模型通式, 如式(8)(9)(10)所示。该延误模型通式不仅不受交叉口信号相位设计的限制, 而且可以准确计算出交叉口内任意两两位置区域之间的行人连续过街延误。

$\begin{matrix} \begin{matrix} D_{(i \to j)}^{+} = [t_{Ri}^{+} + t_{P (i \to j)}^{+} + Δ t_{j}^{+} - \frac{t_{i}^{+}}{2} (\frac{}{} 1 - \\ \frac{q_{(i \to j)}^{+}}{q_{Sj}^{+}}) - t_{0 (i \to j)}^{+}] (q_{(i \to j)}^{+} t_{i}^{+}) (8) \\ D_{(i \to j)}^{-} = [t_{Ri}^{-} + t_{P (i \to j)}^{-} + Δ t_{j}^{-} - \frac{t_{i}^{-}}{2} (\frac{}{} 1 - \\ \frac{q_{(i \to j)}^{-}}{q_{Sj}^{-}}) - t_{0 (i \to j)}^{-}] (q_{(i \to j)}^{-} t_{i}^{-}) (9) \\ {\bar{d}}_{(i \to j)} = \frac{D_{(i \to j)}^{+} + D_{(i \to j)}^{-}}{q_{(i \to j)}^{+} t_{i}^{+} + q_{(i \to j)}^{-} t_{i}^{-}} (10) \end{matrix} \end{matrix}$

式中:变量上标中的正号和负号分别表示沿顺时针和逆时针方向过街时的情况; D₍_i_→_j₎为行人从位置区域i到位置区域j的总延误时间; t_R_i为位置区域i的累积行人红灯时间; t_P(_i_→_j₎为离开位置区域i与走向位置区域j的行人通行相位绿灯启亮时间差; Δ t_j为走向位置区域j的初始行人清空时间; t_i为离开位置区域i的累积行人时间; q₍_i_→_j₎为从位置区域i到位置区域j的连续过街行人达到率; q_S_j为走向位置区域j的人行横道最大通行能力; t₀₍_i_→_j₎为从位置区域i到位置区域j的第一次过街起点与最后一次过街起点之间的步行时间。其中, 沿顺时针与逆时针方向离开位置区域i的累积行人时间之和等于一个信号周期时长, 即 $\begin{matrix} t_{i}^{+} \end{matrix}$ + $\begin{matrix} t_{i}^{-} \end{matrix}$ =C。

对于上述情形(3)而言, 延误模型通式(8)中的符号“ i” 与“ +” 组合等价为关系式(5)中的方向符号“ N” 及位置符号“ A” , 符号“ j” 与“ +” 组合等价为方向符号“ E” 及位置符号“ C” , 式(8)与式(5)一致; 延误模型通式(9)中的符号“ i” 与“ -” 组合等价为关系式(6)中的方向符号“ W” 及位置符号“ H” , 符号“ j” 与“ -” 组合等价为方向符号“ S” 及位置符号“ F” , 式(9)与式(6)一致。

在延误模型通式中, q_S_j由人行横道线的宽度决定, 通常远大于行人达到率q₍_i_→_j₎; Δ t_j由初始等待行人数量和人行横道最大通行能力共同决定, 通常取值较小; t_R_i、t_P(_i_→_j₎、t_i、t₀₍_i_→_j₎则与信号相位设计方案密切相关, 其取值大小直接决定行人连续过街的延误时间大小。

当交叉口内存在多个位置区域之间的连续过街需求时, 建立总的行人连续过街延误模型通式, 如式(11)(12)所示:

$\begin{matrix} \begin{matrix} D = \sum D_{(i \to j)} = \\ \sum (D_{(i \to j)}^{+} + D_{(i \to j)}^{-}) (11) \\ d = \frac{\sum D_{(i \to j)}}{\sum q_{(i \to j)} C} = \\ \frac{\sum (D_{(i \to j)}^{+} + D_{(i \to j)}^{-})}{\sum (q_{(i \to j)}^{+} t_{i}^{+} + q_{(i \to j)}^{-} t_{i}^{-})} (12) \end{matrix} \end{matrix}$

式中:i, j∈ U, U为行人连续过街需求的起止方向集合, 由多组位置区域对组成, 对于图1所示的交叉口而言, U={(A/H, D/E), (C/B, F/G), (E/D, H/A), (G/F, B/C)}。

3 算例分析

以图1所示的交叉口为例, 已知位置点间距AB、CD、EF、GH均为24 m; 位置点间距BC、DE、FG、HA均为6 m; 行人步行速度为1.2 m/s; 连续过街行人到达率为0.2 人/s; 各人行横道最大通行能力均为10 人/s。假设交叉口采用四相位的进口单独放行方式; 信号周期为100 s; 每个机动车/行人信号相位时长为25 s, 其中行人绿灯时间为5 s; 行人红灯或绿闪时间(未进入人行横道的行人应驻足等候, 已进入人行横道的行人可继续通行)为20 s。针对A(H)→ D(E)方向的行人过街需求分析如下:

(1)当交叉口采用顺时针放行方式时, 利用延误模型通式(8)(9)(10), 分别计算行人沿顺时针、逆时针以及不固定方向过街时的延误时间, 如表1所示。

从表1可以看出, 行人沿顺时针方向过街的平均延误时间最小, 且约等于行人在第一次过街前的平均延误时间 $\begin{matrix} t_{Ri}^{+} \end{matrix}$ /2, 说明几乎所有行人在第一次过街后均可实现绿波通行, 即行人绿波带宽等于行人绿灯时间, 带宽占比达到100%, 绿波协调效果达到最佳。

(2)当交叉口采用逆时针放行方式时, 利用延误模型通式(8)(9)(10), 分别计算行人沿顺时针、逆时针以及不固定方向过街时的延误时间, 如表2所示。

从表2可以看出, 行人沿逆时针方向过街的平均延误时间最小, 且约等于行人在第一次过街前的平均延误时间 $\begin{matrix} t_{Ri}^{-} \end{matrix}$ /2, 说明几乎所有行人在第一次过街后均可实现绿波通行, 即行人绿波带宽等于行人绿灯时间, 带宽占比达到100%, 绿波协调效果达到最佳。

(3)当交叉口采用东南北西放行方式时, 利用延误模型通式(8)(9)(10), 分别计算行人沿顺时

针、逆时针以及不固定方向过街时的延误时间, 如表3所示。

从表3可以看出, 由于信号相位相序设置为东南北西时, 可以为A(H)→ D(E)方向的过街行人在顺时针(A→ D)和逆时针(H→ E)两个方向上各形成一条行人绿波带, 因此行人采用不固定方向过街时的平均延误时间最小, 且约等于行人在第一次过街前的平均延误时间 $\begin{matrix} t_{Ri}^{+} \end{matrix}$ /2与 $\begin{matrix} t_{Ri}^{-} \end{matrix}$ /2, 说明几乎所有行人在采用不固定方向第一次过街后均可实现绿波通行, 即行人绿波带宽等于行人绿灯时间, 带宽占比达到100%, 绿波协调效果达到最佳。

当交叉口采用其他信号相位相序设计时, 同样可以利用延误模型通式, 分别计算行人沿顺时针、逆时针以及不固定方向过街时的延误时间。整理A(H)→ D(E)方向3种行人过街方式在各种相位相序设置下的延误时间, 如表4所示。

表1 顺时针放行相位设计下的行人过街延误时间 Table 1 Delay time of pedestrian crossing under signal design mode of clockwise green light s

过街方式	$\begin{matrix} t_{Ri}^{+} \end{matrix}$	$\begin{matrix} t_{Ri}^{-} \end{matrix}$	$\begin{matrix} t_{P (i \to j)}^{+} \end{matrix}$	$\begin{matrix} t_{P (i \to j)}^{-} \end{matrix}$	Δ $\begin{matrix} t_{j}^{+} \end{matrix}$	Δ $\begin{matrix} t_{j}^{-} \end{matrix}$	$\begin{matrix} t_{i}^{+} \end{matrix}$	$\begin{matrix} t_{i}^{-} \end{matrix}$	$\begin{matrix} D_{(i \to j)}^{+} \end{matrix}$	$\begin{matrix} D_{(i \to j)}^{-} \end{matrix}$	$\begin{matrix} {\bar{d}}_{(i \to j)} \end{matrix}$
顺时针	95	-	25	-	2	-	100	0	960	0	48
逆时针	-	95	-	75	-	2	0	100	0	1960	98
不固定方向	20	70	25	75	0.5	1.5	25	75	41	1271	66

表1 顺时针放行相位设计下的行人过街延误时间 Table 1 Delay time of pedestrian crossing under signal design mode of clockwise green light s

表2 逆时针放行相位设计下的行人过街延误时间 Table 2 Delay time of pedestrian crossing under signal design mode of counterclockwise green light s

过街方式	$\begin{matrix} t_{Ri}^{+} \end{matrix}$	$\begin{matrix} t_{Ri}^{-} \end{matrix}$	$\begin{matrix} t_{P (i \to j)}^{+} \end{matrix}$	$\begin{matrix} t_{P (i \to j)}^{-} \end{matrix}$	Δ $\begin{matrix} t_{j}^{+} \end{matrix}$	Δ $\begin{matrix} t_{j}^{-} \end{matrix}$	$\begin{matrix} t_{i}^{+} \end{matrix}$	$\begin{matrix} t_{i}^{-} \end{matrix}$	$\begin{matrix} D_{(i \to j)}^{+} \end{matrix}$	$\begin{matrix} D_{(i \to j)}^{-} \end{matrix}$	$\begin{matrix} {\bar{d}}_{(i \to j)} \end{matrix}$
顺时针	95	-	75	-	2	-	100	0	1960	0	98
逆时针	-	95	-	25	-	2	0	100	0	960	48
不固定方向	70	20	75	25	1.5	0.5	75	25	1271	41	66

表2 逆时针放行相位设计下的行人过街延误时间 Table 2 Delay time of pedestrian crossing under signal design mode of counterclockwise green light s

表3 东南北西放行相位设计下的行人过街延误时间 Table 3 Delay time of pedestrian crossing under signal design mode of east-south-north-west green light s

过街方式	$\begin{matrix} t_{Ri}^{+} \end{matrix}$	$\begin{matrix} t_{Ri}^{-} \end{matrix}$	$\begin{matrix} t_{P (i \to j)}^{+} \end{matrix}$	$\begin{matrix} t_{P (i \to j)}^{-} \end{matrix}$	Δ $\begin{matrix} t_{j}^{+} \end{matrix}$	Δ $\begin{matrix} t_{j}^{-} \end{matrix}$	$\begin{matrix} t_{i}^{+} \end{matrix}$	$\begin{matrix} t_{i}^{-} \end{matrix}$	$\begin{matrix} D_{(i \to j)}^{+} \end{matrix}$	$\begin{matrix} D_{(i \to j)}^{-} \end{matrix}$	$\begin{matrix} {\bar{d}}_{(i \to j)} \end{matrix}$
顺时针	95	-	25	-	2	-	100	0	960	0	48
逆时针	-	95	-	25	-	2	0	100	0	960	48
不固定方向	45	45	25	25	1	1	50	50	215	215	22

表3 东南北西放行相位设计下的行人过街延误时间 Table 3 Delay time of pedestrian crossing under signal design mode of east-south-north-west green light s

表4 A(H)→ D(E)方向行人过街延误时间分析 Table 4 Delay time analysis of pedestrian crossing from A(H)→ D(E) s

由表4可知, 对于A(H)→ D(E)方向的行人过街需求而言, 交叉口的相位相序采用东南北西放行最佳, 其次为顺时针和逆时针放行, 再次为东北南西和东西南北放行, 最差为东西北南放行; 当交叉口采用顺(逆)时针放行方式时, 行人沿顺(逆)时针方向过街的平均延误时间最小, 且在第一次过街后将实现绿波通行, 当交叉口采用其他放行方式时, 则行人沿不固定方向过街的平均延误时间最小。因此需要合理设置信号相位相序和行人引导策略, 以实现行人在信号交叉口处的连续过街通行。而对于其他方向以及多个方向的行人过街需求, 同样可以利用延误模型(8)(9)(10)(11)(12), 分析计算不同相位相序设置方式下行人沿顺时针、逆时针以及不固定方向过街时的延误时间, 从而确定最佳的信号相位相序和行人引导策略组合。

4 仿真试验

针对上述算例, 选用微观交通仿真软件Vissim, 仿真模拟不同信号相位相序设置和行人过街组织方案下A→ D方向行人过街的整体运行效果。由于现有仿真软件难以精确模拟出行人沿不固定方向过街时的路径自主选择行为, 因此分别选取顺时针和逆时针两种过街方式下的行人延误情况进行仿真分析。

根据算例给定的交叉口几何条件和行人交通特性参数, 在Vissim环境中建立仿真交叉口, 通过设定行人采取顺时针或逆时针过街方式时的行走路径, 分别模拟不同信号相位相序设置条件下行人斜穿信号交叉口的行走过程, 并选取平均延误作为最终评价指标输出。

仿真试验得到A→ D方向行人沿顺时针和逆时针方向过街的延误时间, 分别如表5和表6所示。

由表5和表6可以看出, 行人延误时间的仿真结果与模型计算结果非常一致, 其偏差都在3%以内, 从而验证了行人连续过街延误模型通式的准确性和可靠性, 实现了行人斜穿信号交叉口的延误时间准确计算。

表5 A→ D方向行人沿顺时针方向过街的延误时间 Table 5 Delay time of pedestrian crossing clockwise from A to D s

表6 A→ D方向行人沿逆时针方向过街的延误时间 Table 6 Delay time of pedestrian crossing counterclockwise from A to D s

5 结束语

从行人斜穿信号交叉口的实际过街需求出发, 针对不同信号相位相序设置和行人过街组织方案, 利用时距图对行人连续过街进行了绿波分析, 给出了行人连续横穿信号交叉口的绿波带设计方式, 实现了给定方向下行人连续过街的绿波通行; 根据行人到达和离开位置点的时刻线, 推导了行人沿顺时针、逆时针以及不固定方向连续过街的延误模型, 针对交叉口内多个位置区域之间的连续过街需求, 建立了适用于任意信号相位相序设置的行人连续过街延误模型通式, 实现了行人斜穿信号交叉口的延误时间准确计算, 为交叉口信号控制方案的分析评价和优化设计提供了一个新视角。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	高利平, 陈绍宽, 梁肖, 等. 基于人行横道位置的行人-机动车延误模型[J]. 吉林大学学报: 工学版, 2009, 39(增刊2): 47-51. Gao Li-ping, Chen Shao-kuan, Liang Xiao, et al. Delay model of pedestrian-vehicle system based on location of crossing[J]. Journal of Jilin University(Engineering and Technology Edition), 2009, 39(Sup. 2): 47-51. [本文引用:1]
[2]	郭宏伟, 高自友, 赵小梅. 基于持续模型的行人过街行为[J]. 吉林大学学报: 工学版, 2009, 39(增刊2): 35-40. Guo Hong-wei, Gao Zi-you, Zhao Xiao-mei. Pedestrian crossing behaviours based on duration model[J]. Journal of Jilin University(Engineering and Technology Edition), 2009, 39(Sup. 2): 35-40. [本文引用:1]
[3]	Golani A, Damti H. Model for estimating crossing times at high-occupancy crosswalks[J]. Transportation Research Record, 2007, 2002: 125-130. [本文引用:1]
[4]	Alhajyaseen W K M, Nakamura H. Quality of pedestrian flow and crosswalk width at signalized intersections[J]. IATSS Research, 2010, 34(1): 35-41. [本文引用:1]
[5]	Goldschmidt J. Pedestrian delay and traffic management[R]. Berkshire: Transport and Road Research Laboratory, 1977. [本文引用:1]
[6]	Virkler M R. Pedestrian compliance effects on signal delay[J]. Transportation Research Record: Journal of the Transportation Research Board, 1998, 1636: 88-91. [本文引用:1]
[7]	Transportation Research Board. Highway Capacity Manual 2004[M]. Washington DC: National Research Council, 2000. [本文引用:1]
[8]	Japan Society of Traffic Engineers. Manual of Traffic Signal Control[M]. Tokyo: Japan Society of Traffic Engineers, 2006. [本文引用:1]
[9]	冯树民, 裴玉龙. 行人过街延误研究[J]. 哈尔滨工业大学学报, 2007, 39(4): 613-616. Feng Shu-min, Pei Yu-long. Research on delay of pedestrian crossing[J]. Journal of Harbin Institute of Technology, 2007, 39(4): 613-616. [本文引用:1]
[10]	冯树民, 裴玉龙. 考虑行人过街的两相位交叉口配时优化[J]. 交通运输系统工程与信息, 2009, 9(3): 146-151. Feng Shu-min, Pei Yu-long. Timing optimization for two-phase intersections considering pedestrian crossing[J]. Journal of Transportation Systems Engineering and Information Technology, 2009, 9(3): 146-151. [本文引用:1]
[11]	高利平. 城市道路环境下人行横道处行人与机动车冲突分析与延误建模[D]. 北京: 北京交通大学交通运输学院, 2010. Gao Li-ping. Delay modeling on pedestrian-vehicle conflict at crosswalks in urban street[D]. Beijing: School of Traffic and Transportation, Beijing Jiaotong University, 2010. [本文引用:1]
[12]	钱大琳, 陈小红. 基于行人专用相位的交叉口信号控制优化模型[J]. 中国公路学报, 2013, 26(5): 140-147. Qian Da-lin, Chen Xiao-hong. Signal control optimization model at intersection by modifying pedestrian phase[J]. China Journal of Highway and Transport, 2013, 26(5): 140-147. [本文引用:1]
[13]	马万经, 林瑜, 杨晓光. 多相位信号控制交叉口行人相位设置方法[J]. 交通运输工程学报, 2004, 4(2): 103-106. Ma Wan-jing, Lin Yu, Yang Xiao-guang. Design method of pedestrian phases at multi-phase signal intersection[J]. Journal of Traffic and Transportation Engineering, 2004, 4(2): 103-106. [本文引用:1]
[14]	赵韩涛, 郭栋. 有行人专用相位交叉口行人过街时间模型[J]. 哈尔滨工业大学学报, 2012, 44(8): 57-61. Zhao Han-tao, Guo Dong. Model of pedestrians crossing time at signalized intersection with exclusive pedestrian phase[J]. Journal of Harbin Institute of Technology, 2012, 44(8): 57-61. [本文引用:1]
[15]	孙迪. 行人过街交通行为分析建模[D]. 长春: 吉林大学交通学院, 2012. Sun Di. Analysis and modeling of pedestrian crossing behaviour[D]. Changchun: College of Transportation, Jilin University, 2012. [本文引用:1]
[16]	卢凯. 交通信号协调控制基础理论与关键技术研究[D]. 广州: 华南理工大学土木与交通学院, 2010. Lu Kai. Research on the foundational theory and key techniques of coordinate signal control in urban traffic network[D]. Guangzhou: School of Civil Engineering and Transportation, South China University of Technology, 2010. [本文引用:1]

2009

0.0

. 2009, 39(增刊2):47-51

Delay model of pedestrian-vehicle system based on location of crossing

基于人行横道位置的行人-机动车延误模型

Gao Li-ping , Chen Shao-kuan , Liang Xiao

高利平, 陈绍宽, 梁肖

Based on factors of pedestrian and vehicle operation, the delay model on crossing location of pedestrianvehicle interference system was established according to crossing demands of pedestrian and vehicle. Several influence levels along with location of crossing were analyzed. Taking advantages of VISSISM software and one 2lanes branch road in Xicheng District, Beijing as an example, one best location of crossing was developed from the 7 choice locations. The results show that average delay of pedestrian is directly related to the walking distance from starting/ending points to crossing of pedestrian, but indirectly related to average delay of vehicle. The average delay of pedestrian is much bigger than the average delay of vehicle.

基于行人过街需求分布的考虑，分步解析了行人延误和机动车延误的组成因素和变化关系，建立了基于人行横道位置选择的行人机动车系统延误模型，阐述了人行横道位置对相关延误的影响程度，并通过VISSIM仿真软件测算了北京某路段的最优人行横道位置。结果表明：行人平均延误与行人到达人行横道平均距离成正比，远大于机动车平均延误，且与后者成反比。

... 而直角人行横道适用范围更广、灵活性更高,可适用于绝大部分的交叉口,但其施划位置及信号相位应根据行人过街需求分布进行合理设置^[1],以避免行人因为过街等待时间过长而选择违章过街^[2] ...

2009

0.0

. 2009, 39(增刊2):35-40

Pedestrian crossing behaviours based on duration model

基于持续模型的行人过街行为

Guo Hong-wei , Gao Zi-you , Zhao Xiao-mei.

郭宏伟, 高自友, 赵小梅

摘　要：在行人过街行为实测数据基础上,建立了基于危险的行人过街等待持续模型。分别采用非参数形式和参数形式的基准危险函数的模型框架,对影响过街行为的因素,特别是违章过街的影响因素进行了分析。研究结果表明,非参数形式模型对行人过街等待行为描述更为精确;行人的过街行为呈现明显的时间相关性,违章倾向随等待时间的增加而增加。本研究可为行人交通行为分析和行人交通仿真提供有益参考。

2007

0.0

... Golani等^[3]综合考虑行人的起步时间、步行速度、行人间距等影响因素,建立了高占用率人行横道的行人通行时间估算模型 ...

2010

0.0

... Alhajyaseen等^[4]提出了一种针对不同行人需求组合和预定服务水平的人行横道宽度估算方法 ...

1977

0.0

... Goldschmidt^[5]对行人过街延误与交通布局特点之间的关系展开研究,分析了交通流量、道路宽度、信号配时、人群组成等因素对行人过街延误的影响 ...

1998

0.0

... Virkler^[6]考虑行人过街的行为心理对信号交叉口的行人延误公式进行了修正 ...

2000

0.0

... 美国的通行能力手册^[7]和日本的交通信号控制手册^[8]都建立了相应的行人过街时间计算公式 ...

2006

0.0

... 美国的通行能力手册^[7]和日本的交通信号控制手册^[8]都建立了相应的行人过街时间计算公式 ...

2007

0.0

. 2007, 39(4):613-616 DOI:doi:10.3321/j.issn:0367-6234.2007.04.024

Research on delay of pedestrian crossing

行人过街延误研究

Feng Shu-min , Pei Yu-long.

冯树民, 裴玉龙

分析了无信号控制下行人过街的机动车和行人的运行特征、穿插特征,确定了行人穿越机动车的可穿越间隙,针对行人一次穿越一条车道和多条车道出现可穿越间隙下过街两种情况推算出行人过街平均延误的计算方法.分析了信号控制无干扰情况下行人过街的机动车和行人的运行特征,描绘出了行人的聚集和消散示意图,得出行人过街平均延误的计算方法.分析了在信号交叉口处行人过街有干扰情况下行人延误的产生机理,给出行人过街的平均延误计算方法.

... 冯树民等^[9,10]研究了无干扰情况下的信号交叉口行人过街平均延误计算方法,建立了考虑行人过街的交叉口信号配时优化模型 ...

2009

0.0

. 2009, 9(3):146-151 DOI:doi:10.3969/j.issn.1009-6744.2009.03.023

Timing optimization for two-phase intersections considering pedestrian crossing

考虑行人过街的两相位交叉口配时优化

Feng Shu-min , Pei Yu-long.

冯树民, 裴玉龙

分析了信号交叉口的机动车和行人的运行特性,考虑了行人过街与机动车运行的相互影响,为满足行人的安全过街,在两相位交叉口信号配时中加入行人行走的迟起、早断时间.考虑行人过街的需求,在信号配时中将行人过街的最大延误时间以及行人过街的总延误纳入到交叉口信号配时优化模型中,提出以周期、停车率、饱和度、排队长度、行人最大允许延误时间、机动车最大允许延误时间作为约束条件,以机动车和行人的总延误最小为优化目标,建立交叉口信号配时的优化模型,给出求解方法,为信号交叉口的优化配时提出新的思路.

... 冯树民等^[9,10]研究了无干扰情况下的信号交叉口行人过街平均延误计算方法,建立了考虑行人过街的交叉口信号配时优化模型 ...

2010

0.0

. 2010, :- DOI:doi:10.7666/d.y1781785

Delay modeling on pedestrian-vehicle conflict at crosswalks in urban street[D]. Beijing: School of Traffic and Transportation,

城市道路环境下人行横道处行人与机动车冲突分析与延误建模[D]

Gao Li-ping.

高利平

机动车、行人以及非机动车高度混合运行是发展中国家城市道路交通的重要特征,近年来国内外不少学者对混合交通流问题进行了持续深入的研究,丰富了城市交通工程的研究成果。作为道路基础设施的人行横道是城市道路网中行人与车辆“争夺”通行权的重要区域,而在该区域发生的行人与机动车的相互干扰与冲突又是影响关联路段以及周围路网运行效率的重要因素,因此,有必要对人行横道区域范围内的行人过街与机动车运行行为(尤其是相互干扰与冲突行为)进行全面深入地研究。　　论文在全面回顾与讨论国内外有关行人与机动车冲突研究的基础上,结合北京市道...

... 高利平^[11]分析了不同行人过街方式下的信号交叉口行人过街延误情况,建立了信号交叉口基于过街方式的行人延误模型 ...

2013

0.0

. 2013, 26(5):140-147

Signal control optimization model at intersection by modifying pedestrian phase

基于行人专用相位的交叉口信号控制优化模型

Qian Da-lin , Chen Xiao-hong.

钱大琳, 陈小红

Considering the conflict between motor vehicles and slow mode transportation at signal control intersection which has different lane degrees between the two phases under unsaturated state, this paper proposed a new signal control plan for pedestrian signal light by modifying the pedestrian phase under the control of the signal light of motor vehicles. Moreover, the pedestrian delay model and signal timing optimization model were introduced in order to ensure the security of travelers and eliminate the conflict of mixed traffic crossing this intersection. Finally, the intersection between Dongzhimenwai Street and Sanlitun Road was simulated for analysis by using VISSIM simulation software. The results show that when the signal control intersection has the higher mixed ratio of slow mode transportation, the vehicle average delay can decrease by 15.6% and non-motorized transport average delay can decrease by 4%, compared with the measured data. This method is feasible and effective.

为解决未饱和状态下绿灯末期机动车与慢行交通之间的冲突,针对道路等级相差较大的两相位信号控制交叉口,在机动车信号灯兼控行人方案的基础上,对行人专用相位进行修改,提出了一种新的交叉口信号控制方案,并给出了该方案下行人过街延误计算模型以及信号配时参数优化模型,最后运用VISSIM仿真软件对北京市东直门外大街与三里屯路交叉口进行了模拟分析。结果表明:当次干道行人进口道慢行交通流量较大时,车均延误与慢行交通平均延误分别比实测数据降低约15.6%与4%,方案可行有效。

... 钱大琳等^[12]针对道路等级相差较大的两相位信号交叉口,建立了基于行人专用相位的行人过街延误计算模型和交叉口信号配时优化模型 ...

2004

0.0

. 2004, 4(2):103-106 DOI:doi:10.3321/j.issn:1671-1637.2004.02.024

Design method of pedestrian phases at multi-phase signal intersection

多相位信号控制交叉口行人相位设置方法

Ma Wan-jing , Lin Yu , Yang Xiao-guang.

马万经, 林瑜, 杨晓光

运用相位组合技术,对行人相位与机动车相位的各种可能的组合进行了研究,提出了二次过街条件下行人相位的设计方法.与传统行人相位设计方法的对比分析表明这种行人相位设计方法缩短了行人过街最短绿灯时间,降低了过街人均延误.

... 马万经等^[13]研究了行人相位与机动车相位的组合设置问题,提出了多相位信号控制交叉口行人相位的设计方法 ...

2012

0.0

. 2012, 44(8):57-61 DOI:doi:10.11918/j.issn.0367-6234.2012.08.012

Model of pedestrians crossing time at signalized intersection with exclusive pedestrian phase

有行人专用相位交叉口行人过街时间模型

Zhao Han-tao , Guo Dong.

赵韩涛, 郭栋

To determine the time of green light for pedestrians at signalized intersection with exclusive pedestrian phase, a model for estimating crossing times is proposed. The model consists of two parts. The time function for pedestrian crossing refuges is derived using wave theory, and the time function for pedestrian crossing intersection diagonally is an adaptation of existing HCM model. The model attempts to describe the influence of dominant platoon, opposite platoon and rectangular cross pedestrian flow. According to the data extracted from video survey and artificial measurement of four intersections at Weihai, the statistical analysis comes to conclusions. The 15th percentile speed of pedestrians crossing intersection diagonally and non-physical refuges is 1.43 m/s, and that of pedestrians crossing physical refuges is 1.35 m/s. The effective widths of pedestrians crossing intersection diagonally are 9 meters and 12 meters. Finally, the model parameters were calibrated by using SPSS. Results of a case study show that the model can more accurately predict pedestrian crossing time, and the error is within 5％.

为确定有行人专用相位交叉口行人绿灯时间,研究了行人穿越交叉口的过街时间．利用交通波理论推导了行人跨越安全岛的时间函数,考虑同向、对向和交叉行人流的影响,借鉴HCM的行人过街时间模型构建了行人穿越交叉口对角的时间公式．采用录像法和人工测量法对威海市4个交叉口进行调查,统计分析得到:行人穿越交叉口对角和非实体安全岛的15％位速度为1.43 m/s,穿越实体安全岛的15％位速度为1.35 m/s;行人在对角通行的有效宽度为9 m和12 m;利用SPSS标定了模型参数．案例研究结果表明,所建模型能较为准确地预测行人过街时间,误差在5％以内．

... 赵韩涛等^[14]推导了行人过街时间函数,建立了具有行人专用相位的过街时间模型 ...

2012

0.0

. 2012, :-

Analysis and modeling of pedestrian crossing behaviour[D]. Changchun: College of Transportation,

行人过街交通行为分析建模[D]

Sun Di.

孙迪

面对化石能源逐渐枯竭，全球气候变暖，生态环境持续恶化，很多国家提出了环保、绿色低碳的可持续发展理念。越来越多的城市提倡步行、自行车出行以及“自行车+公交+步行”等可持续交通发展模式，尤其是步行、自行车等慢行交通出行方式再次受到推崇。过去几十年，为了适应社会经济快速发展的需求，我国的城市一直本着“以车为本”的理念，在解决交通问题时主要考虑的是机动车的运行效率和安全等，处处以车辆通行优先，以大量挤占和牺牲行人、自行车出行为代价，“肆意”侵占行人和非机动车出行的利益，严重威胁到行人和非机动车出行者的安全。随着“以人为本”的科学发展理念逐步深入人心，城市行人交通已经不再被忽略，行人出行的安全、效率、舒适度等都是处理城市交通问题的重要考虑因素。在城市交通中，过街行人交通是城市交通中一种常见的交通现象。过街行人与机动车流的冲突是造成城市交通效率下降和危险性上升的重要原因。当机动车在通行过程中受到行人过街干扰时，其行为会根据研究地点的不同而做出相应的反应变化，同样，当行人在过街过程中受到机动车通行的干扰时，行人往往会受到其心理因素及道路因素等影响而做出与交通环境相适应的行为决策。对行人及机动车交通行为进行合理的分析，可为道路通行效率及道路通行安全评价等问题的解决提供理论基础。此外，在对交叉口及路段实施交通管制时，应结合管制位置处的行人及机动车的行为特点，有针对性的提出相应的控制方法，进而提升该路段或交叉口的通行效率及过街安全性。由此可知，对行人过街情况下人与车交通行为的研究具有一定的现实意义。本学位论文对过街行人影响下的交通行为及相关控制方法进行了深入研究，主要包括以下四方面：（1）行人过街特性分析总结分析了行人过街的行为特性，在此基础上，对行人过街轨迹特性进行分析。主要利用视频采集方法对行人过街过程中的位置及速度的变化进行数据采集，以此为基础，计算了行人在过街中各位置的平均步速。此外，利用“混合交通运动轨迹跟踪分析软件”对行人过街轨迹进行采集，并对调查区域进行坐标标定，得到行人过街时空轨迹曲线图，以反映行人过街过程中位置及速度的变化情况。通过对位置及速度的变化情况分析，得到行人过街轨迹的影响因素。将不同性质的影响因素分类，并利用社会力基础理论对不同影响因素产生的虚拟作用力进行建模，得到多个因素的虚拟力模型。将不同影响因素产生的虚拟力进行合成，最终得到行人过街过程中综合因素产生的虚拟合力模型。（2）考虑对向行人干扰的行人过街效率分析对行人过街方式进行了阐述，将行人过街行为划分为一次过街和二次过街两种方式，并对不同过街方式特点进行分析。基于此，将常用的行人过街效率计算方法分为行人延误及通行能力两类，通过比较两类方法的特点，选择行人人均延误作为行人过街效率指标进行进一步分析。针对过街双向行人之间互相干扰的特点，以流体力学理论为基础，建立对向行人干扰情况下行人过街延误模型。此外，针对行人二次过街的复杂特性，将行人二次过街划分为两个阶段，按照行人到达情况的不同，将行人过街分为六种情况，并在考虑对向行人干扰以及行人消散延误基础上，建立不同情况下行人过街延误模型，并对延误模型进行参数标定。（3）考虑行人和机动车违章的行人过街效益分析对行人过街行为影响下的行人与机动车违章行为影响因素进行分析，并从行人及机动车违章行为角度出发，通过交通调查得到机动车违章相关数据，利用Logistic方法对机动车违章影响因素进行建模，提取影响机动车违章行为的主要参数，并通过Hosmer and Lemeshow指标对模型进行检验，检验结果证明该模型可较为准确反映机动车的违章行为。此外，分别针对行人违章及机动车违章两种情况，并考虑到行人间的相互干扰情况，利用间隙理论建立相应的效率及安全指标模型。最后，利用乘法合成法，将不同的指标进行合并，建立既考虑效率又考虑安全的综合效益指标，并绘制出不同违章率下的综合效益指标曲线图。（4）单位进出口路段的行人-机动车信号控制本章首先对城市道路一类特殊路段——单位进出口路段的交通特性进行了分析，重点研究了行人流与各向机动车流的冲突特性。针对该类路段人-车冲突特性，提出了进入单位左转车流-行人流交通控制方法，利用概率论和间隙理论建立了左转车影响下的直行车延误模型，并在此基础上提出了两种控制方案。通过理论推导和仿真实例验证，对比分析了两方案在不同条件下的适用性。此外，深入分析在不同控制策略下过街行人与右转驶入单位进出口机动车流冲突特性，以此为基础，总结了右转机动车流的信号控制条件，并进一步考虑机动车违章及行人互扰等行为，建立了右转机动车不同违章率下的行人人均延误模型，由此确定了单位进出口处右转机动车信号设置条件。

... 孙迪^[15]针对过街双向行人之间互相干扰的特点,建立了对向行人干扰情况下的过街延误模型 ...

2010

0.0

. 2010, :-

Research on the foundational theory and key techniques of coordinate signal control in urban traffic network[D]. Guangzhou: School of Civil Engineering and Transportation,

交通信号协调控制基础理论与关键技术研究[D]

Lu Kai.

卢凯

随着城市交通量的增长与路网密度的增强,交叉口之间的相关性日益明显,如何从整个系统战略角度出发,进行有效的交通信号协调控制设计,已成为城市交通控制发展的新要求。本文针对现有交通信号协调控制理论方法的不足,结合现代城市交通信号控制的发展需求与技术特点,在交通控制子区的动态划分、绿波协调控制模型的建立、停车延误协调控制模型的建立、交通信号协调控制关键技术的实现等方面进行了相关研究与探讨,完成的主要科研工作与取得的重要研究成果概括如下: 1.通过分析相邻交叉口间距、路段交通量以及交叉口信号配时参数等因素对相邻交叉口关联性的作用影响,提出了一个定量化描述相邻交叉口之间关联性强弱的交通参量——相邻交叉口关联度,并对其计算方法与科学合理性进行了相关论述,进一步给出了多交叉口组合关联度的定义与计算公式,实现了交叉口之间相关性要素的有效综合;通过将各控制子区划分方案映射为相应字符解、设置基于交叉口关联度的子区划分约束条件、选取评判子区划分方案优劣的评价指标,建立了一套基于交叉口关联度分析的控制子区划分模型,设计了一套完整的最佳控制子区划分方案获取流程,采用子区划分层扩散算法实现了对控制子区划分方案的综合性分析评价,并通过算例分析对基于交叉口关联度分析的控制子区划分方法进行了详细阐述与有效性验证。 2.改进了进口对称放行方式下的双向绿波协调控制经典数解算法,提出了基于公共信号周期允许变化范围的理想交叉口间距取值范围确定法则,给出了基于偏移绿信比概念的绿波带宽度计算方法,建立了最大偏移绿信比最小化的最佳理想交叉口间距选取原则;设计了进口单独放行方式下的双向绿波协调控制数解算法,实现了公共信号周期、信号相序组合以及相位差的优化设计,并通过理论与算例分析有效验证了进口单独放行方式下双向绿波协调控制数解算法的适用范围特点与正确有效性;建立了进口混合放行方式下的通用双向绿波协调控制模型,设计了一套基于协调控制模型的信号配时优化流程,利用混合整数线性规划方法实现了控制模型的优化求解,并给出了不同带宽需求下的双向绿波协调控制目标函数通式,为干道双向绿波协调控制设计提供了一种适用面广、实用性强、准确度高的新方法。 3.分析了上游交叉口信号相位设置对下游交叉口获取理想停车延误协调控制效果的影响,针对未饱和与过饱和两种不同交通状态,根据行驶车队头车到达下游交叉口进口道的不同时刻,利用交叉口进口道车辆停车延误分析图,分别建立了相应的停车延误协调控制模型,得到了行驶车队停车延误与相邻交叉口相对相位差之间的函数关系,并设计了基于停车延误协调控制模型的信号配时优化流程,给出了信号相位绿信比与交叉口相位差的优化方法;通过公式推导与仿真分析验证了未饱和与过饱和两套基准阻滞停车延误模型的一致性和准确性,从基准阻滞和随机与过饱和阻滞两个方面分析比较了不同控制方式与不同交通状态下的交叉口进口道停车延误。 4.通过对比现有交通信号控制系统的结构框架,提出了一种动态分层式区域交通信号控制结构,构建了控制系统的物理框架与逻辑框架,描述了控制系统的硬件组成与功能模块;建立了交通信号控制系统的路网实时信息数据库,设计了控制子区快速动态划分流程,研究了交叉口关联度大小与协调控制方式选取之间的对应关系,确定了协调控制最佳信号配时方案的选取依据,给出了一种协调控制方案快速平滑过渡算法;以东莞市虎门镇连升路交通信号协调控制系统设计为例,依次介绍了单交叉口的信号配时设计、控制子区的划分步骤流程以及最佳信号配时方案的计算选取过程,并通过交通仿真分析与实际系统运行,综合有效地验证了本文所述控制子区划分理论与协调控制模型方法的科学合理性。

... 但由于交叉口的信号相位设计通常需要考虑进口道机动车放行以及干道车队协调控制^[16]的要求,且行人在交叉口处总的延误时间还应包括其第一次过街前的等待时间,因此需要进一步建立行人连续过街的延误模型,以便于量化分析不同信号相位相序设置和行人过街组织方案的优劣 ...