作者简介:潘述亮(1986-),男,助理工程师,博士.研究方向:新型公共交通系统规划与设计.
在已知乘客需求和车队规模的条件下,以综合考虑出行者(包括最小化乘客等待接驳公交车时间、最小化乘客实际乘坐与期望乘坐主线公交的时间差值)和运营者(最小化车辆运营时间)双方利益为优化目标,建立了灵活型接驳公交路径优化和协同调度的同步优化模型。由于该模型目标函数为非线性,本文为求解方便将其进一步转化为混合整数规划模型,并采用基于重力模型的一种启发式算法对模型进行求解,最后通过实例验证了该调度模型的可靠性和实用性。
A rout planning and coordinated scheduling model is developed to minimize the passenger's costs, including the waiting time and the difference between actual transfer time and the expected transfer time, and the operator cost, the total travel time of the vehicles, with considering the known passenger demands, fleet size and the departure time of the main line at the transfer hub. As the objective of this model is a nonlinear function, the model is transferred into a mixed integer programming model for the convenience of resolution. In the resolving process, a gravity-based heuristic method is employed to solve the model rapidly. A case study is given to illustrate the reliability and practicability of the proposed model.
如何改善城市公共交通骨干网络的接驳服务是现今公交系统规划设计和管理中亟待解决的问题。一个好的综合公交运输系统能够通过运营更短的线路、消除骨干网络与接驳公交的重复线路以及提供高质量的服务来提高线路覆盖率和减少旅行时间, 进而降低运营成本, 增加运营收入[1]。现有的接驳系统仍在使用定点定线的固定型接驳服务模式[2, 3, 4, 5, 6, 7]。该模式大多面向高峰小时客流需求, 注重规模化成本效率, 对非高峰客流需求(如低密度客流地区、低运输需求时段)及特殊需求乘客缺乏深入考虑, 无法应对多样化的居民出行需求。因此, 灵活型公交接驳系统(Flexible feeder transit, FFT)被提出以解决常规公共交通服务未能有效覆盖的盲点区域市民出行难的问题。目前已有的针对灵活型公交服务调度优化的研究更多集中在可变线路式服务系统上。该系统中的车辆围绕一条由若干站点组成的基准线路运行, 并允许车辆可以在任意两个固定站点之间规定的松弛时间内偏离基准线路。针对该系统的调度问题, 学者们建立了离线优化模型[8]、混合整数规划模型[9, 10, 11]以及插入式启发算法[12, 13, 14], 但均没有考虑与主线公交运营时间的有效协同。然而, 灵活型接驳公交系统仅在线路终点(或起点)存在一个固定站点, 车辆的运行线路和调度方案完全根据预约乘客的需求和换乘站的车辆到站时间而动态优化确认[15, 16]。鉴于此, 本文在给定乘客需求和车队规模的条件下, 以乘客在换乘枢纽/站点的等待服务时间最短为目标, 就该系统的线路优化和协调调度问题建立了一种混合整数规划模型, 并提出了一种基于新型重力模型的启发式求解算法。
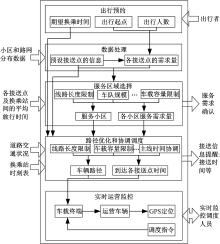
灵活型公交接驳系统通过将常规固定接驳服务的经济性与需求响应服务(如出租车等)的灵活性相结合来提供一种近似个性化的出行服务[17]。如图1所示, 可以根据乘客需求动态地规划线路和车辆调度方案, 灵活地提供预约出行服务。对于传统的固定型接驳公交服务而言, 其线路设计和调度是两个相对独立的过程, 一般会在线路设计完成后进行车辆作业计划的制定和车辆调度。然而, 灵活型接驳公交服务由于需要根据乘客预约的出行需求来进行作业调度, 因此对其的研究是一个线路路径优化和协调调度的同步优化的过程。同时, 以打通城市公交微循环为目的的灵活型公交接驳服务车辆往往行驶于道路条件较为狭窄复杂的城市支路网(如支路网不规则、连通性差等), 并且由于广泛存在的大院制小区使得运营车辆无法进入小区内部为乘客提供上下客服务, 乘客往往集聚在指定的小区门口作为上车点/落客点。为此, 本文设计的灵活型接驳公交服务流程可概括如图2所示。
(1)出行预约:具有出行需求的乘客需要通过电话或者网站等系统提前对其出行需求进行预约。根据系统提示步骤输入其期望换乘时间、出行起点以及出行人数等信息完成预约, 乘客可以预约一次出行, 也可以预约一段时间内的出行。
(2)数据处理:调度中心处理系统根据预约的乘客需求点来设定车辆需要经过的接送点。鉴于国内大院制小区特点, 本文借鉴交通规划中“ 交通小区” 的概念, 将每个住宅小区作为一个或若干个交通小区, 并将其抽象成位于其小区门口的乘客需求点(即乘客接送点)并计算每个接送点的预约需求量。
(3)服务区域确定:调度中心根据所有预约的乘客需求等信息, 以及道路交通状况获取任意需求点与换乘站之间的平均旅行时间等数据, 调用服务区域优化选择模块, 对车辆运营的服务区域以及服务区域内每个接送点需要服务的乘客数量进行优化计算。在优化过程中, 以实际路网为边界, 抽取每个小区的形心作为需求聚集点, 进而得到抽象道路网络, 利用离散优化模型进行求解。该过程完成后, 会对乘客的预约信息进行需求服务确认。对于未能服务的乘客, 则需要考虑选用其他交通方式出行。
(4)路径优化和协调调度:根据已经被确认服务的接送点及其每个乘客需求的期望换乘时间、主线公交发车时刻表等信息, 通过车辆路径优化和协调调度模块来完成每辆车服务路径的优化以及协调调度方案的制定。在优化过程中需要考虑到一些实际的约束, 如单条线路的距离区间限制、车载容量限制等。在该步骤完成后, 会对需要服务的乘客提供接送信息提醒, 主要包括接送时间和估计到站时间等信息, 以便预约的乘客合理安排其出行。
(5)实时运营监控:将每辆车的运行线路以及到达每一接送点的时间下载到车载终端并告知驾驶员。在车辆的实际运营过程中, 每辆车都会实时将位置信息传回调度中心, 以便中心进行实时调控。同时调度中心的调度指令也可以下发到每一辆运营的车辆上, 进而完成运营实时监控和调度。
其中步骤(3)和(4)是系统设计需要解决的关键科学问题。笔者之前已经对步骤(3)的相应内容进行了研究[18, 19], 在此不再赘述。本文研究聚焦在第(4)步, 即根据服务区域选择优化结果(第(3)步结果输出)有效、科学地组织接驳车辆运送服务区域内的乘客由接送点至换乘站。该问题旨在满足所有乘客出行需求的基础上, 同时优化接驳车辆的服务路径和协同调度方案, 使得乘客在最短的时间内换乘上其所期望的车辆, 同时尽可能降低每条线路的运营成本。
根据1.1节中关于灵活型接驳公交系统的运营管理流程, 对模型的建立提出如下假设:
(1)每个需求点的位置和乘客预约需求量均已知。
(2)预约后, 每个乘客期望换乘的主线公交的大致发车时间已知。
(3)需要接驳的主线发车时间点已知。
(4)乘客到站上车的服务时间为常数。
(5)接驳车辆的平均行驶速度已知。
(6)接驳车辆的载客容量已知。
(7)接驳车辆车队车数已知。
该协调调度优化模型可表示为如下一个非线性规划模型:
s.t.
式(1)为目标方程, 包含3个部分:①最小化所有接驳车辆的行驶时间, 以降低运营成本; ②最小化所有乘客在换乘站的等待服务时间, 以降低乘客的时间成本; ③最小化乘客实际乘坐主线公交时间与期望乘坐主线公交的时间差值, 以提高服务质量。
约束(2)和(3)表示对于每一个需求点, 最少有1辆车服务, 最多有Nv辆车服务; 约束(4)表示最多有N辆车参与运营; 约束(5)表示除了每一车辆服务的第一个需求点, 对于其他每个被服务的需求点, 驶入的车辆数应该相等驶出的车辆数; 约束(6)是为了避免在车辆路径中出现回路; 约束(7)和(8)保证每一辆车均将乘客运送到最终目的地— — 换乘站; 约束(9)可以确保每一辆接驳车辆的载客量不会超过其额定载客量, 保证服务水平; 约束(10)表示任何一个需求只能被一辆车服务; 约束(11)表示一辆接驳车辆只能接驳换乘站的一个主线发车时刻点; 约束(12)表示主线公交的每一发车时刻至少有1个需求需要接驳; 约束(13)保证所有被服务的需求等于已知的预约需求量; 约束(14)是变量X和Y之间的数学关系式, 表示一旦一个需求被车辆服务, 则必定至少有一辆车从该需求所在的需求点开出前往其他需求点或换乘站; 车辆的最大和最小线路长度由约束(15)和(16)给出; 约束(17)和(18)表示如果两个站点被一辆换乘车辆先后相邻服务到, 则车辆服务后一站点中的需求的到达时间应等于服务上一需求点中的需求的到达时间加上在上一站点的所有需求服务时间和在两个需求点之间的行驶时间之和; 约束(19)和(20)表示接驳车辆的最后一个需求站点上乘客到达换乘站的时间应等于车辆到达该需求点的时间加上在该站点所有乘客的服务时间和在这两个需求点之间的行驶时间; 约束(21)保证车辆到达换乘站的时间不晚于换乘站主线公交的发车时间, 同时给乘客留有换乘时间δ 。
由于该模型的目标函数中乘客实际换乘主线公交的发车时间与期望换乘主线公交发车时间的差值是绝对值项, 因此需要对目标函数进行线性化处理, 将模型转化为混合整数规划模型。
定义变量Zr为需求r实际换乘主线公交的发车时间与期望换乘主线公交发车时间的差值绝对值, 如式(22)所示:
同时在上述模型的约束条件中加入如下约束:
至此, 将非线性模型转化为了混合整数规划模型, 以方便求解。
本文提出的模型为混合整数规划问题, 作为一类典型的NP-hard问题, 其计算量随着问题规模的增大呈指数形式增长, 因此这类问题常采用启发式算法求解。受到用于出行分布预测的重力模型的启发, 本文提出来一种基于重力模型的启发式算法, 从而将集成的车辆路径优化和协同调度问题转化为求解车辆路径选择链的迭代重力最大化问题。选择链的反向顺序即为优化的车辆行驶路径。基于重力模型的启发式算法的详细步骤介绍如下。
首先, 根据如下步骤完成对出行乘客需求的分配, 保证所有乘客期望与实际换乘主线公交发车时间之间的差值尽可能小。
Step1 分别计算每个乘客需求r期望换乘主线公交时间Tr与实际主线公交|T|个发车时间Tt之间的差值的绝对值Ω t=|Tt-Tr|, 因此每个乘客需求需要计算|T|次时间差值。
Step2 针对每个乘客需求, 找出最小时间差值对应的实际主线公交发车时间, 并初步确认将其接驳到该主线公交车站。如果出现有相同的最小时间差值, 则考虑优先将其接驳到期望时间之前的最近一班车的实际发车时间。
Step3 根据车队规模Nv与主线公交发车时间T的集合元素数量的关系, 按照如下规则处理:
Step3.1 如果Nv≥ |T|, 则不作处理, 统计计算每个需要接驳乘客的发车时间对应的每个接送点的乘客需求量; 反之, 转到Step3.2。
Step3.2 对每一个发车时间Tt中分配的乘客需求量求和, 计算出总的接驳需求量, 并根据总需求量对Tt按照降序排列。
Step3.3 取前Nv个发车时间作为实际乘客接驳时间, 原接驳到该Nv个发车时间的乘客需求不变。
Step3.4 对于原定接驳到其他|T|-Nv个发车时间的乘客需求, 重新计算每一个乘客需求到达该Nv个发车时间的时间差的绝对值。
Step3.5 针对每一乘客需求, 分别找出最小时间差值对应的实际主线公交发车时间, 并确认将其接驳到该主线公交车站。如果出现有相同的最小时间差值, 则考虑优先将其接驳到期望时间之前最近一班车的实际发车时间。
Step3.6 结束。
基于重力模型的启发式算法, 将路径优化问题转化为求解各接驳点之间吸引重力最大化的选择链迭代问题。迭代后选择链的反向顺序即为优化的车辆行驶路径。
任意两个接送点之间的吸引重力定义如下:
式中:Di为从接送点i前往换乘站的客流需求量; tij为接送点i与接送点j之间旅行时间。
需要注意, 在计算一个接送点与换乘站之间重力时, 换乘站的客流需求量可以定义为较大的数值。两个接送点之间的重力值越高, 说明这两个接送点之间单位时间内的需求越大, 并且服务的费用越低, 需要优先服务。在计算接送点与换乘站之间的吸引重力时, 可以将换乘站的客流量设为一个很大的整数M。
在已知车队规模Nv及车辆的额定车载容量Q的条件下, 给出模型的启发式求解算法的步骤如下:
Step1 针对每一个分配有接驳乘客需求的发车时间, 分别计算各接送点以及接送点与换乘站之间的吸引重力模型。如果一个接送点没有接驳到该发车时刻的乘客需求, 可以在计算该发车时间的吸引重力矩阵时排除该接送点。
Step2 取t=1, 针对第一个接驳发车时间, 从换乘站开始, 找出与该换乘站吸引重力最大的接送点, 将其加入选择链; 以该节点为新的起点, 继续选择, 依次加入选择链, 并计算选择链的长度以及已服务需求量。
Step3 如果长度超出最大线路长度限制或者服务的乘客需求量超过车载容量Q, 则转入Step4; 否则, 返回Step 2。
Step4 令t=t+1, 返回Step2; 若t> |T|, 说明针对每一接驳发车时间, 均已经计算出一条车辆服务路径, 则转入Step5; 否则返回Step2。
Step5 依次计算每一接驳发车时间剩余的需求服务的乘客量, 如果某一发车时间的需求全部服务, 则从时间列表删除该时间, 否则转到Step6。
Step6 计算剩余的接驳发车时间数t'和车辆数n', 如果t'=0, 则转到Step7; 如果t'> n', 则返回Step 3继续执行; 否则返回Step1继续执行。
Step7 确定是否所有需求量均已被服务, 如果是, 则转到Step9; 如果不是, 则转到Step8。
Step8 找出任一未被服务的需求, 同时计算其期望时间与所有车辆服务需求未达到额定容量同时线路长度没有超出最大长度限制的车辆所接驳时间的差值, 找出差值最小的那一车辆并根据Step1和Step2的方法重新计算车辆路径, 将其需求加入到该车辆的服务范围中。计算加入后的车辆路径长度, 如果超出限制, 则取消加入, 选择差值较小的另一车辆再次计算加入, 完成后转到Step7。
Step9 结束。
本步骤对2.2节生成的车辆路径采用2-optimization(2-opt)算法进行优化。
Step1 先对每一辆车的服务路径内部进行2-opt优化, 确保每一辆车服务路径对应的服务时间最短。此种情况下, 乘客在换乘站期望乘车时间与实际乘车时间之间的差值并不会发生改变, 随着车辆服务路径的优化, 每一辆车的全部服务时间会减少。与此同时, 通过调整每一辆车的初始发车时间可以使得所有乘客在换乘站的等车时间保持最小不变。
Step2 对服务于同一接驳时间点的车辆之间进行路径优化, 首先检查服务于同一接驳时间点的不同车辆是否有服务相同的需求点的情况。如果有, 则在保证满足车载容量的前提下先合并同一需求点的需求到同一车辆的路径中。随后, 在保证满足车载容量的前提下每次找出两辆车的服务路径进行2-opt优化。
Step 3 对服务于不同接驳时间点的车辆之间进行路径优化, 按照2.2节中的方法进行2-opt优化。只是在确定是否可以交换时, 需要同时考虑目标函数中第1和第3部分的函数值之和是否减少, 再决定是否交换。
根据车辆路径、车辆每服务一个需求所需要的时间以及乘客在换乘站的等车时间最短来决定每一车辆的发车时间以及到达每一需求点的时间。
利用一个小型网络对上述模型进行案例求解以验证上述模型的准确性和适用性, 该模型输入的已知条件如表2~表4所示。表2中给出了一些常变量的输入参数。每个需求点的需求量在表3中列出, 每个需求点之间以及需求点与换乘站之间的平均旅行时间以矩阵的形式在表4中列出, 其中Dij为需求点; H为换乘站。
| 表2 案例中的常变量 Table 2 Parameters of the case study |
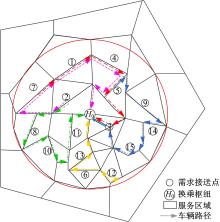
通过使用本文提出的启发式算法对该数值案例进行了求解, 得到每一车辆的服务路径、服务的需求量以及到达每一需求点的时间如表5和图3所示。30个出行需求全部服务, 其中仅有6个乘客的期望到站时间与实际到站时间不符。
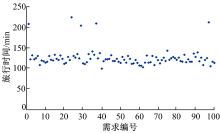
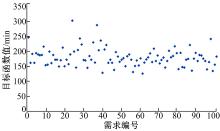
为了进一步验证算法的可靠性, 将表1中常变量中的最大线路长度由6.25 km改为8.75 km, 需求量由30个改为35个, 其他常变量不变, 案例网络的旅行时间矩阵表3不变, 对100组随机产生的15个需求点的35个出行需求量进行模型测试, 测试结果如图4~图6所示。在所给条件下, 将35个出行需求全部服务完成所需车辆数为4~5辆; 95%的车辆总旅行时间为100~150 min, 平均每辆车的旅行时间为20~30 min, 可见启发式算法求解出的车辆的旅行时间结果较为稳定。乘客期望换乘线路的时间与实际换乘线路的时间的绝对差值分布不均, 即便需求分布存在很大的不确定性, 但由于模型和算法的鲁棒性较高, 所以仍然可以生成较为稳定可靠的结果, 总的目标函数值受总旅行时间分布的影响大部分仍集中在150~225之间。同时, 所有100组数据的求解时间均在10 min以内, 使得本文提出的算法能够应用到实际的系统中, 可以在预约和提供服务之间有限的时间窗口内完成车辆路径优化和协同调度。
| 表3 需求点的需求量 Table 3 Demand of each point |
| 表4 案例网络的旅行时间矩阵 Table 4 Travel time matrix for each point min |
| 表5 每一辆车的服务路径、服务时间和服务的需求量 Table 5 Route, time and demand of each vehicle |
针对灵活型接驳公交系统与换乘枢纽主线公交的协调调度问题进行了研究。通过使用网络分析方法, 建立了以最小化所有车辆的运营时间、乘客等车时间和乘客实际换乘时间与期望换乘时间之间的差值最小为优化目标的路径规划和协调调度同步完成的优化模型并进行了实例验证。同时给出了基于改进重力模型的启发式求解算法。算例结果表明, 在车辆调度过程中, 该模型和算法能在合理的时间内求解出有效、合理的车辆服务路径和到达每一需求点的时间。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|