加速度传感器的定义式为:

asen=a+gi (1)

式中:a_sen为传感器采集到的加速度值; a为车辆行驶的加速度值, 它是车速的微分量; g为重力加速度值; i为道路坡度。

对式(1)做微分运算得:

a'sen=a'+gi'(2)整理后有:i'=a'sen-a'g3

式(3)可用于估计道路坡度的变化率信息。由于需要求解的坡度变化率包含大量的噪声, 需要运用滤波算法对坡度变化率信息加以处理。待滤除的噪声主要有传感器采集过程中的噪声和微分运算产生的高频噪声。分析这两项噪声产生的原理可知噪声的性质均应为高斯噪声。而最小二乘算法可以在保证较好跟随性的前提下滤除大量的高斯噪声, 故而坡度变化率的估计选用最小二乘算法。

为了保证较好的实时性, 本文选用含遗忘因子的最小二乘算法来滤除噪声, 最小二乘算法的计算公式如下:

θ^t+1=θ^t+γt+1Zt+1-φTt+1θ^tγt+1=Ptφt+1[φTt+1Ptφt+1+λ]-1Pt+1=1λI-γt+1φTt+1Pt4

式中:估计的参数 θ^=i'; 观测量φ =1; 输出量Z=(a'_sen-a')/g; λ 为遗忘因子; I为单位矩阵; γ 为增益矩阵; P为对称矩阵。

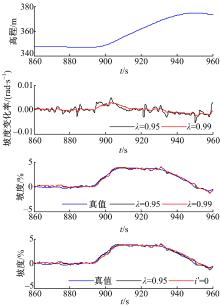
图1为坡度变化率估计结果, 可以看出原始数据中包含大量噪声, 经过最小二乘滤波后噪声有明显改善, λ 取值越大, 得到的结果越平滑, 相应的时间延迟也越大。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 道路坡度变化率估计结果Fig.1 Estimation results of road grade change rate

建立运用整车车速和传感器加速度估计道路坡度的卡尔曼滤波器, 会涉及到整车速度和行驶加速度信息。根据作者已有的研究结论^[10], 包含整车行驶速度、车辆行驶加速度的两参数汽车运行工况具有马尔可夫性, 利用速度与加速度关系的运动学公式和跟驰模型, 车辆行驶速度和加速度的二维状态动力学过程可以表述为:

vt+1at+1=1dt01-δdtvtat (5)

式中:δ =0.9为驾驶员反应强度系数。

考虑在此模型的基础上加入坡度信息建立三维状态转移方程, 根据坡度变化率的表达式(式(3)), 则有离散形式下任意时刻道路坡度计算公式如下:

it+1=it+i'tΔt (6)

建立包含车速、车辆加速度和道路坡度的三维状态转移模型有:

vt+1at+1it+1=1dt001-δdt0001vtatit+00i'tΔt (7)

式中:[v a i]^T=X为状态向量; 1dt001-δdt0001=A为状态转移矩阵; (0 0 i'_tΔ t)^T=U为控制向量。

模型的观测量是由纵向车速和加速度传感器采集到的加速度信息, 根据单轴加速度传感器定义式(1)建立形如Z_k=h Xk的观测方程:

vasen=10001gvai (8)

式中: vasenT=Z, 为观测向量; 10001g=H, 为观测向量矩阵。

至此, 建立了状态估计的状态方程和观测方程。接下来利用式(9)进行道路坡度的估计:

X^t+1-=fX^t, Ut, 0Pt+1-=At+1PtATt+1+QkKt+1=Pt+1-HTt+1Ht+1Pt+1-HTt+1+Rt+1-1X^t+1=X^t+1-+Kt+1Zt+1-hX^t+1-, 0Pt+1=I-Kt+1Ht+1Pt+1-(9)

式中: X^t+1-为预测结果; X^t+1为更新后的结果; Z_t+1为观测变量; P为协方差矩阵; K_t+1为卡尔曼增益; Q和R分别为系统误差和测量误差, 在仿真中:

Q=10-710-210-7; R=0.1520.132。

图2为算法的整体结构, 该坡度估计算法的结构融合了RLS和KF, 分别选取不同的估计模型是充分考虑各变量自身的物理特性。因为道路坡度变化率是一个相对慢变的物理量, 并不需要很高的实时性, 使用含遗忘因子的RLS估计相对慢变坡度变化率是合理的。另一方面, KF算法包含车速和加速度, 是快变量, 用KF估计道路坡度可以保证结果的实时性。此外, RLS模型中还有效利用了KF的估计结果, 式(2)中的a'利用KF输出的状态变量a_est求导所得, 这样可以有效避免对车速二次求导产生大量噪声使信号失真。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 坡度估计算法流程图Fig.2 Overview of road grade estimation algorithm

选取了吉林省境内国道G303为试验路线。试验车为某款重型牵引车, 试验车驾驶室后方的车架上加装单轴加速度传感器, 用DEWE同步采集车辆CAN总线信息、加速度传感器信息和GPS信息。

表1中列举了试验过程中采集到的信息, 其中离线计算的“ 真值” 将在2.2节详细讲述。

表1

Table 1

表1(Table 1)

表1 采集的试验数据 Table 1 Test data acquisition 信号来源 变量 符号 单位 DEWE系统 采样时间 Ts s GPS (VBOX) 纬度 Lat (° ) 经度 Long (° ) 高程 Alt m GPS车速 vGPS km/h CAN ABS从动轴车速 v km/h 加速度传感器 纵向加速度 asen m/s2 离线计算 坡度“ 真值” (GPS) iGPS % 坡度“ 真值” (加速度传感器) isen %

表1 采集的试验数据 Table 1 Test data acquisition

为了方便坡度估计算法的评价, 需要获取真实道路坡度信息进行定量的对比分析。然而真实道路坡度的测量受试验条件的限制, 在长达几十公里的试验路线上逐点测量道路坡度是不现实的。本文将利用加速度传感器信息离线计算道路坡度, 用于接下来的算法效果评价。

利用加速度传感器计算道路坡度的原理是利用加速度传感器的定义式(1), 道路坡度可用下式计算:

i=asen-ag10

为了得到平滑的道路坡度信息, 坡度计算公式中所需的传感器加速度和整车加速度(车速的微分量)需要经过低通滤波处理。由于传统的低通滤波器在消除噪声的同时会产生相位延迟的现象, 离线的“ 真值” 计算使用零相移滤波器对数据进行处理。该滤波器采用正反双向滤波消除了传统单向滤波的相位差。

图3为一段坡度连绵起伏地段的坡度估计结果, 在坡度变化率比较大的阶段坡度结果均有时间延迟, 但是随着时间的推移, RLS模型可以估计出正确的道路坡度变化率, 进而正确修正坡度估计的一步预测结果, 坡度估计结果中的时间延迟可以被有效降低, 而不含坡度变化率的坡度结果将会始终保持这种延迟。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 坡度估计结果时间序列图(组1)Fig.3 Time series of estimated road grade(group1)

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 坡度估计结果时间序列图(组2)Fig.4 Time series of estimated road grade(group2)

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 道路坡度估计结果及其误差的时间序列Fig.5 Time series of estimated road grade and error

图4中曲线的前半段展示了近似为平路的估计结果, 虽然高程曲线显示在该路段上高程几乎是不变的, 但是无论是离线“ 真值” 还是在线估计结果都是在0附近波动, 并且在该路段坡度变化率对坡度估计结果并无显著影响。因为在平路上, 真实的坡度变化率几乎为零, 所以无论是选择了不同的最小二乘遗忘因子还是直接将坡度变化率置零对坡度估计结果均没有显著影响。

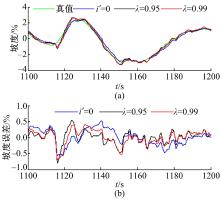
误差的定义是在每一时刻坡度的估计值与“ 真值” 的差值。图5为在不同参数下, 坡度估计结果和其误差的时间序列。

选择一些误差的统计指标进行评价, 包括误差均值, 误差绝对值的均值, 误差标准差和误差最大值。表2为平路的误差统计结果和总体的误差统计结果。注意表中的%与坡度的单位一致, 并不是表达误差占真值的百分比。

从表2可以看出, 由于数据精度较好, 不论是否使用坡度变化率估计模型, 所有坡度估计的结果的误差都不是很大。坡度估计的误差最大值均不超过1%, 误差绝对值的均值不超过0.3%。

平路的误差结果显示:引入坡度变化率表达坡度变化率会使估计结果的噪声含量增加, i'=0的误差结果要比其他的小, 但是增加噪声是非常小的。总的来说, 坡度估计结果对坡度变化率的噪声含量并不敏感。

表2

Table 2

表2(Table 2)

表2 坡度估计结果误差统计 Table 2 Error statistics of grade estimation results % 误差 均值 误差绝对 值的均值 误差 标准差 误差 最大值 平路 (860~890 s) λ =0.95 0.185 0.219 0.179 0.505 λ =0.99 0.185 0.216 0.182 0.507 i'=0 0.188 0.211 0.173 0.491 坡路 (1100~1200 s) λ =0.95 0.012 0.152 0.205 0.795 λ =0.99 0.009 0.180 0.228 0.715 i'=0 0.012 0.209 0.253 0.585

表2 坡度估计结果误差统计 Table 2 Error statistics of grade estimation results %

总体的误差则显示用坡度变化率的结果要好于不使用坡度变化率的结果, 使用较低的遗忘因子可以使误差更小。但是, 这种瞬时偏差很大程度上是延迟带来的。

时间延迟是评价坡度估计结果的重要参数, 在整车控制中对坡度的实时性要求较高。本文用于评价坡度估计时间延迟的方法来源于ISO评价体系中一种用于测量车辆操纵稳定性响应情况的试验规范^[11]。该试验用于评价在行驶路径为一个正弦函数输入下, 车辆瞬态开环响应效果, 在试验过程中提出了一种用于测量方向盘转角与车辆侧向加速度和横摆角速度的时间延迟的方法。

这种测量时间延迟方法的思路是:在选定的、依照一定步长划分的延迟时间范围内, 依次对输入信号做响应时间的延迟, 得到延迟的输入信号, 计算延迟的输入信号和响应信号的相关系数, 绘制延迟时间与相关系数函数, 在相关系数最大时对应的延迟时间就是输入信号与响应信号间的时间延迟。

Rxyτ=1T∫0Txtyt+τdt (11)

依据该方法计算图3试验数据的时间延迟和对应的最大相关系数, 结果如表3所示。

随着坡度变化率估计算法中遗忘因子的增大, 坡度的时间延迟增大, 含坡度变化率的坡度估计模型时间延迟可以控制在1 s以内。 为了获取更小的时间延迟效果, 遗忘因子的推荐取值是0.95。

表3

Table 3

表3(Table 3)

表3 延时效果计算结果 Table 3 Result of time lag calculation 最大相关系数 最大相关系数对应的 时间延迟/s λ =0.95 0.994 0.2 λ =0.99 0.996 0.6 i'=0 0.998 1.3

表3 延时效果计算结果 Table 3 Result of time lag calculation