本文采用的汽车驾驶模拟器平台是由车载单元、5通道投影系统及音响系统组成(见图1)。该模拟器通过加装转角传感器、加速度传感器等实时采集车辆当前位置信息、车速、加速度、前轮转角以及车道偏移量等17个不同维度的数据变量。此外, 该汽车驾驶模拟系统能够对驾驶过程中出现的违法驾驶行为(包括超速、闯红灯、驶出车道)进行自动识别。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 五通道汽车驾驶模拟器Fig.1 Five channel driving simulator

本文共计招募15名具有中华人民共和国C1驾照的驾驶人(其中包括9名男性, 6名女性, 平均年龄为(25.1± 2.8)岁)开展模拟驾驶试验。为了能够更加准确地反映实际驾驶的特性以及当前存在的危险驾驶行为, 选取的试验路段为城市道路, 双向双车道, 期间包含信号灯、行人穿越、周边车辆超越、出现事故等多种场景。具体试验过程如图2所示, 数据的采集及流向如图3所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 试验过程图Fig.2 Process of experiment

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 数据采集图Fig.3 Data collecting

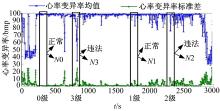
研究表明^[12], 当遭遇危险或者出现驾驶异常时, 驾驶人容易出现紧张或者焦虑等负面情绪, 直接体现为驾驶人心率发生显著变化; 同时, 在负面情绪影响下, 交通事故的发生率将显著提高。因此在统计意义上, 单位时间内心率变化率和违法次数可反映驾驶行为的危险水平。通过对驾驶人心率变化率进行K-均值聚类^[13]并融合驾驶过程中的违法行为, 可以将驾驶行为险态自动划分为4级:0级表示非常安全; 1级表示存在小风险, 只需注意, 无须改变当前状态; 2级表示危险, 需采取操作进行规避; 3级表示非常危险, 需要通过强制减速等方式才能避险。其具体的分级过程如式(1)所示:

D=0, (S∈N0)⋂T=01, (S∈N1)⋂T=02, ((S∈N2)⋂T=1)⋃ ((S∈N3)⋂T=0)3, (S∈N3)⋂T=1 (1)

式中:D为驾驶行为险态等级; S为驾驶人心率变化率, 通过聚类分析可以将其分为N0, …, N3四类, N0为第1类, 其聚类中心为0.684 bmp, N1为第2类, 其聚类中心为4.853 bmp, N2为第3类, 其聚类中心为9.951 bmp, N3为第4类, 其聚类中心为19.186 bmp; T表示该过程中是否出现违法, 0表示未出现, 1表示出现。

根据分类规则对试验数据进行处理分析, 得到有效样本20 219个, 部分驾驶行为险态等级分类如图4所示。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 驾驶行为险态分级Fig.4 Definition of driving risk status

马尔科夫毯是一种由Koller等^[14]于1996年首次引入到工程应用领域的特征提取方法。其定义和计算方法如下。

定义1 给定一个特征f_i, 设特征子集M_i∈ F(f_i∩ M_i≠ f_i), 则称M_i是f_i的马尔科夫毯, 当且仅当在给定M_i的条件下, f_i与F-M_i-{f_i}是独立的, 即

PF-Mi-fi, Mi=PF-Mi-fiMi (2)

推论1 如果特征子集M_i是f_i的马尔科夫毯, 那么在给定M_i的条件下, f_i与类别C也是独立的, 即:

PCfi, Mi=PCMi (3)

马尔科夫毯方法的特点是可以有效地对无关和冗余的特征进行约减或者消除。通过对获取的多维数据进行离散化, 将驾驶行为险态作为目标节点变量, 利用马尔科夫毯学习法(Markov blanket, MB))选取对驾驶行为险态具有显著性影响的特征, 其实现过程如下^[14]。

(1)输入各变量的离散数据、变量的取值范围(如速度V取值为0~140 km/h)、目标变量节点T。

(2)启发式搜索与因变量相关的变量。

(3)利用独立性测试条件去除错误节点, 进而获取目标节点的父子节点集合PC(T)。

(4)从集合PC(T)的父子节点PC中利用条件依赖性寻找目标变量节点的配偶节点。

(5)输出目标变量节点的马尔科夫毯。

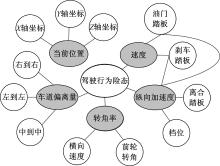
由PCMB算法得到驾驶行为险态的马尔科夫毯为车辆当前位置、速度、纵向加速度、前轮转角变化率和车道偏离量(见图5)。然后寻找集合PC(T)中各个节点的父子节点, 得到5个变量的父子节点为图中非阴影节点。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 驾驶行为险态马尔科夫毯Fig.5 Markov blanket of driving risk status

采用马尔科夫毯算法选取与驾驶行为险态相关的影响变量, 能够有效地避免现有方法中选取相关变量的主观性, 但是所选择的自变量与因变量之间不一定存在着显著的相关性和因果关系。基于此, 本文采用kendall的tau-b相关系数和Spearman秩相关系数方法对选取变量与驾驶行为险态之间的关系进行分析, 结果如表1所示。

表1

Table 1

表1(Table 1)

表1 基于马尔科夫毯特征选取的相关性检验 Table 1 Correlation test for features based on Markov blanket 特征 驾驶行为险态 kendall的tau-b 相关系数方法 Spearman秩 相关系数方法 Sig.(双侧) 相关系数 Sig.(双侧) 相关系数 当前位置 0.000 -0.025* * 0.000 -0.028* * 速度 0.001 0.123* * 0.000 0.152* * 纵向加速度 0.016 0.013* 0.004 0.021* * 转角率 0.000 0.022* * 0.000 0.024* * 车道偏移量 0.000 -0.053* * 0.000 -0.066* * 注:* * 表示在置信度(双侧)为0.01时, 相关性是显著的; * 表示在置信度(双侧)为0.05时, 相关性是显著的。

表1 基于马尔科夫毯特征选取的相关性检验 Table 1 Correlation test for features based on Markov blanket

从表1可知, 选取置信度为0.05时(当观测的显著性水平小于0.05时, 拒绝原假设, 认为两变量之间存在线性相关性), 通过马尔科夫毯算法选取的当前位置、速度、纵向加速度、前轮转角变化率以及车道偏离量与驾驶行为险态显著相关(Sig.< 0.05), 其中当前位置、车道偏离量与驾驶行为险态显著负相关, 其余特征与驾驶险态正相关。由此可见, 采用马尔科夫毯方法进行驾驶行为险态关联性特征提取是较为合理的。

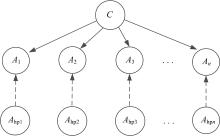
隐朴素贝叶斯模型(Hidden Naive Bayes, NHB)的特点是在原朴素贝叶斯模型的基础上采用给每个属性节点引入一个隐藏变量来表示其与其他各节点之间的相互依赖关系。其结构上主要包括根节点、属性节点和隐藏的父节点3类节点, 分别用C、A、A_hp表示, 其结构图如图6所示。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 隐朴素贝叶斯结构Fig.6 Structure of Hidden Naive Bayes

在驾驶行为险态辨识过程中, 可以将驾驶行为险态作为图6中的根节点C, 而通过马尔科夫毯选择出的5个特征变量可以定义为模型中的节点A, 则A_hp为其属性节点的父节点。由此HNB的联合概率P(A₁, …, A_n, C)可以定义为:

PA1, …, An, C=PC∏Pi=1nAiAhpi, C (4)

式中:P(C)为节点C的先验概率。

P(Ai|Ahpi, C)=∑Wijj=1, j≠inPAiAj, C, ∑Wijj=1, j≠in=1 (5)

此外, 为了能够将构造过程简单化, HNB算法采用了贝叶斯毯分类器中剔除的条件互信息, 式(5)中W_ij可表示为:

Wij=Ip(Ai, Aj|C)∑j=1, j≠inIp(Ai, Aj|C) (6)

式中:I_p(A_i, A_j|C)表示了两个属性之间的条件互信息。

从本质上说, 每个节点变量A_i上所依赖的隐父节点是所有对该属性A_i有影响的依赖性关系的权值的总和。而HNB是一种限制性的贝叶斯分类器, 在进行驾驶行为险态辨识时, 其驾驶行为险态辨识c(E)定义为:

c(E)=argmax_{c∈ C}P(c) ∏i=1nP(a_i|a_hpi, c) (7)

式中:P(a_i|a_hpi, c)为事件a_i和a_hpi同时发生的概率^{[15, 16]}。

隐朴素贝叶斯模型不仅具有运行效率高、结构简单等特点, 还能够表达节点变量之间的关系。本文基于My Eclipses和Matlab平台对算法进行实现, 其具体的计算流程如图7所示。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 驾驶行为险态辨识流程Fig.7 Process of identifying driving risk status

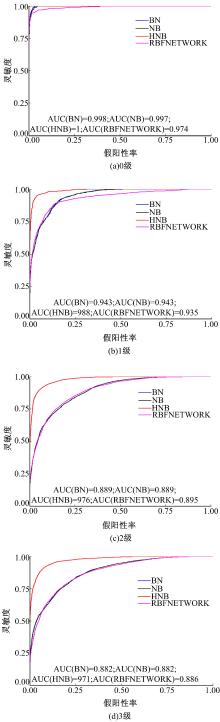
对于所有的试验数据集, 本文采用十折交叉法进行对比验证, 即将所有的数据集分成10份, 轮流将其中9份作为训练集, 剩余1份作为测试集, 将10次的结果均值作为对算法精度的估计。此外, 为了验证所构建模型的优越性和有效性, 本文还分别采用朴素贝叶斯(NB)、贝叶斯网络(BN)和径向基神经网络(RBFNETWORK)三种算法进行建模。通过采用如图7所示的计算方法, 得到4种辨识方法的辨识精度的各项数据如表2所示。由表2可知, 基于HNB算法的驾驶行为险态辨识算法在判断正确率(TP Rate=0.904, FP Rate=0.066)和预测精度方面(Precision=0.906, Recall=0.904, F-measure=0.975)都比NB、BN及RBFNETWORK算法优异。此外, 本文采还从ROC曲线面积及训练用时两个方面对4种不同辨识算法的优劣进行比较分析, 结果如图8所示。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 不同风险等级时的ROC曲线Fig.8 ROC curve in different risk status levels

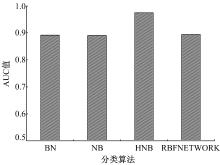
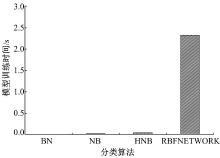
从图8(a)~(d)中可以看出, 采用HNB算法对驾驶行为险态4个不同等级辨识时, 其ROC面积分别达到1、0.988、0.976、0.971, 都处于非常高的水平, 同时与其他3种分类算法相比, HNB模型对不同的险态行为的辨识效果都最为理想。由此可见, 采用HNB算法构建驾驶行为险态辨识模型相较于其他算法具有显著的优越性。另外从图9可以看出, 本文选取的HNB算法的曲线下面积(Area under curve, AUC)平均值高于其他3种算法, 说明该算法在准确性识别方面更具优势。此外, 通过对模型训练时间(见图10)的分析发现, HNB算法相较于NB和BN算法虽然训练时间略长, 但是差异性不明显(与BN算法训练时间差异为0.03 s), 而相比于RBFNETWORK算法则具有较明显的优势, 实时性较强。

表2

Table 2

表2(Table 2)

表2 辨识结果分析 Table 2 Result of identification 辨识方法 TP Rate FP Rate Precision Recall F-Measure BN 0.767 0.171 0.771 0.767 0.768 NB 0.765 0.172 0.770 0.765 0.767 HNB 0.904 0.066 0.906 0.904 0.975 RBFNETWORK 0.776 0.719 0.776 0.776 0.776

表2 辨识结果分析 Table 2 Result of identification

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 四种算法的平均AUC值Fig.9 AUC of four algorithms

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 四种算法训练用时Fig.10 Training time of four algorithms