异形桥梁损伤识别方法及参数影响分析

引用本文

赵云鹏, 于天来, 焦峪波, 宫亚峰, 宋刚. 异形桥梁损伤识别方法及参数影响分析. 吉林大学学报:工学版, 2016, 46(6): 1858-1866
ZHAO Yun-peng, YU Tian-lai, JIAO Yu-bo, GONG Ya-feng, SONG Gang. Damage identification method and factor evaluation for irregular-shaped bridge. Journal of Jilin University Engineering and Technology Edition, 2016, 46(6): 1858-1866 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201606014
Permissions

异形桥梁损伤识别方法及参数影响分析

赵云鹏^1,², 于天来¹, 焦峪波³, 宫亚峰³, 宋刚³

1.东北林业大学土木工程学院,哈尔滨 150040

2.辽宁省交通规划设计院,沈阳 110166

3.吉林大学交通学院,长春 130022

焦峪波(1986-),男,讲师,博士.研究方向:桥梁智能诊断.E-mail:jiaoyb@jlu.edu.cn

作者简介:赵云鹏(1981-),男,高级工程师,博士研究生.研究方向:桥梁设计与检算.

基金项目:国家自然科学基金项目(51408258); 中国博士后科学基金项目(2014M560237,2015T80305); 中央高校基本科研业务费专项资金项目(JCKY-QKJC06); 吉林省科技厅青年科研基金项目(20160520068JH)

摘要

针对现有异形桥梁结构损伤识别方法的局限性和参数影响的不确定性,本文首先详细分析了损伤程度、传感器数量和模态阶次等参数对损伤识别指标(振型差、模态曲率差、模态柔度差及其曲率)的影响效果,确定将模态柔度差曲率作为识别指标。其次,提出异形桥梁两阶段损伤识别方法,在采用模态柔度差曲率实现损伤定位基础上,基于遗传算法优化支持向量机对损伤程度进行准确识别。损伤识别结果验证了该方法的有效性和准确性。

关键词: 道路工程; 异形桥梁; 损伤识别; 模态柔度差曲率; 遗传算法; 支持向量机

中图分类号:U446 文献标志码:A 文章编号:1671-5497(2016)06-1858-09

Damage identification method and factor evaluation for irregular-shaped bridge

ZHAO Yun-peng^1,², YU Tian-lai¹, JIAO Yu-bo³, GONG Ya-feng³, SONG Gang³

1.School of Civil Engineering, Northeast Forestry University, Harbin 150040, China

2.Traffic Planning and Design Institute of Liaoning Province, Shenyang 110166, China

3.College of Transportation, Jilin University, Changchun 130022, China

Abstract

Traditional damage identification methods are difficult to accurately identify the damage location and extent of irregular-shaped bridge because of the complex structure of the bridge. To overcome the shortcoming of these damage identification methods and the uncertainty of factor influence, the factor effect on damage identification indicator is synthetically analyzed, and a novel damage identification approach for irregular-shaped bridge is proposed based on modal flexibility difference curvature and Support Vector Machine optimized by Genetic Algorithm (SVM-GA). First, the damage identification effect on the indicators (modal shape change, modal curvature difference, modal flexibility difference and curvature) is studied under the impacts of damage severity, number of sensors and modal orders. Second, the two stage damage identification method for irregular-shaped bridge is presented. On the basis of determining the damage location using modal flexibility difference curvature, the damage extent is forecasted and identified based on SVM-GA. Damage identification results demonstrate that the proposed method is feasible and accurate.

Key words: road engineering; irregular-shaped bridge; damage identification; modal flexibility difference curvature; genetic algorithm(GA); support vector machine(SVM)

Show Figures

0 引言

桥梁在车辆荷载、环境侵蚀及材料老化的作用下, 结构损伤不断出现^[1]。异形桥梁由于特殊的构造形式, 受力状态复杂, 损伤更为普遍。传统的损伤识别指标和方法对异形桥梁具有一定的局限性, 提出适用于该桥型的损伤识别方法对于保障城市立交桥的安全运营具有重要的应用价值。

基于结构振动特性的损伤识别方法具有测试方便、精度高和易于获取等优点, 在桥梁健康监测和损伤识别中得到了广泛的应用^[2]。基于动力参数的损伤识别指标包括频率、振型、模态曲率、频响函数和模态柔度等^{[3, 4, 5]}。Jassim等^[6]采用频响参数和模态置信准则(Modal assurance criterion, MAC)进行了悬臂梁的损伤诊断和识别。Cao等^[7]提出了改进的模态曲率指标, 具有较好的抗噪能力, 室内试验验证了对多位置损伤识别的有效性。张军等^[8]采用模态柔度差曲率和进行三维结构损伤识别, 克服了模态柔度差曲率指标的漏判现象。对各损伤识别指标的准确性和适用性进行分析, 选择有效的异形桥梁损伤识别指标, 能够确保识别结果的可信度。同时, 基于计算智能的结构损伤识别方法正成为桥梁损伤识别的重要手段, 如基于神经网络、遗传算法、支持向量机、模糊理论的损伤识别方法。Guo等^[9]提出了基于贝叶斯理论和免疫遗传算法的结构多位置损伤识别方法。孙宗光等^[10]采用BP神经网络对悬索桥数值模型进行损伤预测, 准确度达到86%。然而, 总结现有研究成果发现:神经网络采用梯度下降算法, 参数设置繁琐, 收敛速度慢^[11]; 支持向量机依赖部分关键数据, 降低了模型的复杂程度, 具有较好的预测能力^[12]; 遗传算法采用遗传操作进行最优解全局搜索; 遗传优化支持向量机算法实现了两种算法的补充和优化, 在预测分析方面具有独特的优势。

考虑到基于动力特性的损伤识别指标具有较大的不确定性, 其损伤识别结果受到诸多因素的影响。本文重点研究了损伤程度、传感器数量和模态阶次等参数对常用损伤识别指标(振型差、模态曲率差、模态柔度差及曲率)的影响, 确定了识别效果好、性能稳定的损伤识别指标。在此基础上, 提出了基于模态柔度差曲率和遗传优化支持向量机的异形桥梁损伤识别方法, 该方法能实现异形桥梁损伤的准确识别和判定, 识别结果验证了所提出方法的有效性和准确性。

1 异形桥梁概况

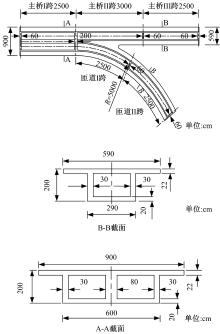
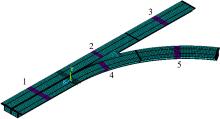
选取典型异形桥梁为损伤识别研究对象^[13]。该桥梁由主桥和匝道组成, 整体布置如图1所示。

异形桥梁采用C50混凝土; 材料弹性模量为3.5× 10¹⁰ Pa; 密度为2500 kg/m³; 泊松比为0.2。采用Solid45实体单元建立异形桥梁ANSYS模型, 选取各跨跨中2 m范围内单元为损伤单元(见图2)。损伤程度通过降低单元弹性模量模拟, 如式(1)所示:

$\begin{matrix} α_{i} = 1 - E_{m, d} / E_{m, u} \end{matrix}$ (1)

式中:m为单元号; α _i为单元损伤程度; E_m_{, u}、E_m_{, d}分别为单元损伤前、后的弹性模量。

	Figure Option View Download New Window
	图1 典型异形桥梁平面图Fig.1 Typical irregular-shaped bridge

	Figure Option View Download New Window
	图2 异形桥梁损伤单元选取Fig.2 Damaged sections of irregular-shaped bridge

2 参数影响不确定性分析

本文主要针对常用损伤识别指标的参数影响不确定性进行分析, 包括振型差、模态曲率差、模态柔度差及其曲率。以第4跨跨中损伤为例, 评价指标的准确性。其中, 模态振型差的计算公式为:

$\begin{matrix} \bar{φ} = φ^{d} - φ^{u} \end{matrix}$ (2)

式中: $\begin{matrix} \bar{φ} \end{matrix}$ 为损伤前、后振型差值; φ ^u、φ ^d分别为结构损伤前、后的模态振型值。

模态曲率可以通过振型对位置的二阶导数计算得到, 如式(3)所示:

$\begin{matrix} φ ″_{j, i} = \frac{φ_{(j + 1), i} - 2 φ_{j, i} + φ_{(j - 1), i}}{l^{2}} \end{matrix}$ (3)

式中:i为模态阶次; j为节点号; l为测点间距。

模态曲率差为结构损伤后与损伤前模态曲率的差值, 如式(4)所示:

$\begin{matrix} \bar{φ″} = φ ″_{d} - φ ″_{u} \end{matrix}$ (4)

式中:φ ″_u、φ ″_d分别为结构损伤前、后的模态曲率。

结构模态柔度矩阵的计算公式为:

$\begin{matrix} F = \overset{n}{\sum_{i = 1}} \frac{1}{ω_{i}^{2}} φ_{i} {φ^{T}}_{i} \end{matrix}$ (5)

式中:ω 为结构的模态频率; φ _i为模态振型。

模态柔度差矩阵为损伤前、后的模态柔度矩阵之差, 如式(6)所示:

$\begin{matrix} ΔF = F_{u} - F_{d} \end{matrix}$ (6)

对模态柔度差矩阵Δ F按列取绝对值最大值, 组成模态柔度差向量f, 对其进行二次中心差分, 计算得到模态柔度差曲率, 如式(7)所示:

$\begin{matrix} CF C_{j} = \frac{f_{j + 1} - 2 f_{j} + f_{j - 1}}{2 l^{2}} \end{matrix}$ (7)

2.1 损伤程度对损伤识别的影响

桥梁结构损伤的产生和发展往往是一个渐变的过程, 呈现由轻微到严重的阶段性变化。所以, 损伤程度是桥梁损伤识别的重要影响参数之一。

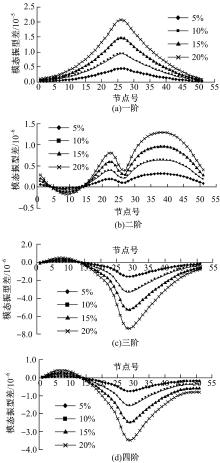
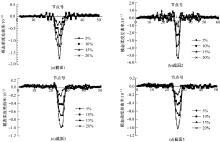
截面4(见图2)损伤后的前四阶模态振型差如图3所示, 损伤程度分别为5%、10%、15%和20%。

由图3可以看出, 一、三、四阶模态振型差在跨中损伤位置处出现峰值, 且与损伤程度具有较好的相关性。由于二阶模态振型为正弦曲线, 跨中损伤位置的振型值为零, 造成对跨中损伤的不敏感。基于模态振型的变化可以看出, 振型差能够实现损伤位置识别, 且与损伤程度的变化趋势相一致。

	Figure Option View Download New Window
	图3 截面4损伤后前四阶模态振型差Fig.3 First four modal shape changes before and after damage for section 4

损伤后的前四阶模态曲率差值变化如图4所示。

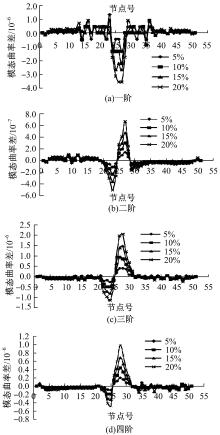	Figure Option View Download New Window
	图4 截面4损伤后前四阶模态曲率差Fig.4 First four modal curvature difference changes before and after damage for section 4

由图4可以看出, 前四阶模态曲率差曲线在结构损伤位置附近均出现峰值, 与损伤程度成正比例关系, 可以用于损伤定位及程度识别。特别是二阶振型对损伤不敏感的情况下, 模态曲率差能准确反映损伤的位置及程度, 具有良好的识别效果。

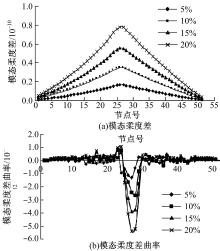
损伤后的模态柔度差与模态柔度差曲率变化如图5所示。模态柔度差指标的变化趋势与振型差指标相似。模态柔度差曲率指标在损伤位置处出现峰值, 其损伤位置识别效果优于模态柔度差指标。

	Figure Option View Download New Window
	图5 截面4损伤后模态柔度差及曲率变化Fig.5 Modal flexibility difference and curvature changes before and after damage for section 4

2.2 传感器数量对损伤识别的影响

传感器数量是影响损伤识别指标准确性的关键因素。2.1节中分析了51个测试传感器的损伤识别指标结果, 将传感器数量依次调整为26、14、8, 分析各工况下指标的损伤识别效果。

通过分析损伤识别指标的变化曲线可知, 模态振型差和模态柔度差随损伤的变化呈现整体性改变, 而模态曲率差和模态柔度差曲率具有良好的局部损伤识别能力。因此, 分别建立两类评价指标。

对于模态振型差和模态柔度差, 建立损伤中心偏移率指标进行定量分析。截面4损伤单元的相关节点为24、25、26、27和28。定义识别出的曲线峰值中心到实际损伤中心(26号节点)的距离为评价参数, 如式(8)所示:

$\begin{matrix} γ = \frac{|S_{d} - S_{a}|}{S_{a}} \times 100 \end{matrix}$ (8)

式中:γ 为中心偏移率评价指标; S_d、S_a分别为识别出的和实际的损伤中心节点。

模态曲率差和模态柔度差曲率具备良好的局部损伤识别能力, 以节点集合的相关性为评价参数, 如式(9)所示:

$\begin{matrix} η = \frac{N (I ⋂ A)}{N (I ⋃ A)} \times 100 \end{matrix}$ (9)

式中:η 为节点集合相关性评价指标; I、A分别为识别出的损伤单元节点集合和实际损伤单元节点集合, 本文中A=[24 25 26 27 28]; N(I∩ A)、N(I∪ A)分别代表I和A并集和交集中元素的数量。

一、三和四阶模态振型差的损伤中心偏移率如表1所示。可以看出, 三、四阶的偏移率大于一阶, 说明一阶振型差的识别效果优于三、四阶。随着传感器数量的减少, 损伤中心偏移率γ 有增大的趋势, 损伤识别的精度降低。

模态柔度差随传感器数量变化的损伤中心偏移率如表2所示。模态柔度差指标损伤中心受传感器数量的影响较小, 其偏移率为0。损伤程度对模态柔度差指标的识别影响不明显。

表1 振型差指标不确定性评价 Table 1 Uncertainty analysis for modal shape change index

表2 模态柔度差指标不确定性评价 Table 2 Uncertainty analysis for modal flexibility change index

为对比模态柔度差曲率和模态曲率差的局部损伤识别能力, 分别计算不同传感器数量下损伤识别指标的不确定性, 如表3和表4所示。从表3可以看出:在传感器数量充足的情况下, 模态柔度差曲率指标的准确性满足要求, 但随着传感器数量的减少, 精度逐渐降低。从表4可以看出:在传感器数量为51时, 模态曲率差的节点相关性较高且随着传感器数量的减少, 精度下降迅速。相同条件下, 模态柔度差曲率指标优于模态曲率差指标。

表3 模态柔度差曲率指标不确定性评价 Table 3 Uncertainty analysis for modal flexibility curvature change index

表4 模态曲率差指标不确定性评价 Table 4 Uncertainty analysis for modal curvature change index

2.3 模态阶次对损伤识别的影响

传感器数量为51时, 分别采用第一、三阶和第一、三、四阶模态振型差之和计算识别中心偏移率评价指标, 如表5所示。从表5可以看出:“ 第一阶+第三阶” 评价指标γ 小于“ 第一阶+第三阶+第四阶” , 两者均小于第一阶模态振型差指标。说明增加模态阶次并不能提高模态振型差指标的识别精度, 一阶模态振型差即可实现损伤中心区域的判定。

表5 不同模态数量下模态振型差指标识别效果 Table 5 Identification effect for modal shape changes under different modal numbers

模态柔度指标由模态频率和模态振型计算得到。所以, 增加模态阶次可以提高模态柔度指标的准确性, 但对其损伤识别结果的影响难以确定。分别选取第一阶、前三阶、前六阶模态参数计算模态柔度差及模态柔度差曲率指标, 其识别准确性评价指标如表6所示。从表6可以看出:第一阶模态柔度差就能实现损伤区域的准确识别; 前六阶模态数据计算得到的模态柔度差曲率损伤识别评价指标优于第一阶和前三阶的计算结果, 表明增加模态阶次的数量, 可以提高模态柔度差曲率识别损伤的准确性和有效性。

表6 不同模态数量下模态柔度差及曲率、模态曲率差指标识别效果 Table 6 Identification effect for modal flexibility changes and curvature, modal curvature changes under different modal numbers

采用前二阶、前三阶和前四阶的模态数据计算模态曲率差的和, 相应的损伤识别评价指标结果列于表6中。结果表明:增加模态阶次, 模态曲率差指标的识别精度不仅没有提升, 反而逐渐下降, 说明可以仅采用一阶模态数据计算的模态曲率差进行损伤识别。

3 异形桥梁损伤识别方法

3.1 遗传优化支持向量机算法

遗传优化支持向量机算法采用遗传操作(选择、交叉、变异)寻找支持向量机算法的最优参数c和g。将得到的优化参数作为训练模型的参数, 实现结构损伤程度识别。其基本结构体系如图6所示。

	Figure Option View Download New Window
	图6 遗传优化支持向量机结构Fig.6 Structure of optimized SVM using GA

3.2 损伤位置识别

在各跨跨中建立损伤单元(见图2), 单位置损伤以各截面损伤为研究对象, 损伤程度为5%、10%、15%及20%。对于多位置损伤, 损伤工况如表7所示。

表7 多位置损伤定位工况 Table 7 Cases of damage identification with multiple damage locations

通过对各损伤识别指标的参数影响不确定性分析发现, 模态振型差、模态柔度差属于整体性指标, 虽稳定性较好, 但对于局部损伤不敏感。模态曲率差和模态柔度差曲率为局部损伤指标。对比发现, 模态柔度差曲率的识别精度优于模态曲率差, 受到传感器数量及模态数量的影响较小。所以, 在异形桥梁各跨损伤识别中, 选取局部损伤识别精度高且稳定性好的模态柔度差曲率进行损伤识别。

采用模态柔度差曲率进行截面1~5的单位置损伤识别, 截面4损伤识别结果如图5所示, 截面1、2、3、5的识别结果如图7所示。

从图7可以看出, 模态柔度差曲率能够实现对异形桥梁单损伤位置的识别, 且效果良好。分叉处截面2、4受力状态复杂, 所以识别结果曲线变化相对复杂, 但不影响识别结果的判定。

对多损伤工况进行损伤识别, 以工况2为例, 识别结果如图8所示。可以看出, 同时存在多位置损伤时, 模态柔度差曲率也能实现损伤的准确定位。

3.3 损伤程度识别

以模态柔度差曲率值为遗传优化支持向量机的输入参数, 单元损伤程度为输出参数。

(1)单位置损伤识别

以截面2、3、4损伤为研究对象, 损伤程度分别为0%、5%、10%、15%和20%共15个样本为训练样本, 选取3%、8%、18%共9个样本为测试样本。测试样本损伤程度识别结果如表8所示。

	Figure Option View Download New Window
	图7 单位置损伤识别Fig.7 Damage identification for single damage location

	Figure Option View Download New Window
	图8 多位置损伤识别Fig.8 Damage identification for multiple damage localizations

可以看出, 单位置损伤程度识别最大误差为3.0%, 具有较高精度, 说明建立的遗传优化支持向量机识别方法具有良好的单位置损伤程度识别能力。

(2)多位置损伤识别

以截面2和4、4和5同时发生损伤为研究对象, 损伤识别工况如表9所示。选取3%-15%、5%-20%、18%-12%共6个样本为相应的测试样本, 损伤识别结果如表10所示。多位置损伤程度识别最大误差为4.94%, 损伤程度识别精度较高, 说明该方法具备良好的多位置损伤程度识别能力。

表8 基于模态柔度差曲率的遗传算法优化支持向量机单位置损伤程度识别 Table 8 Damage identification with single damage location using GA-SVM and modal flexibility difference curvature

表9 多位置损伤程度识别工况 Table 9 Cases of damage extent identification with multiple damage locations

表10 基于模态柔度差曲率的遗传算法优化支持向量机多位置损伤程度识别 Table 10 Damage identification with multiple damage locations using GA-SVM and modal flexibility difference curvature

4 结论

(1)建立了损伤识别指标识别效果的评价指标, 采用识别中心偏移率对整体性损伤识别指标进行评价, 采用节点集合相关性对局部损伤识别结果进行评价, 两指标具有良好的适用性。

(2)综合分析了损伤识别指标的参数影响不确定性和识别结果的准确性, 模态柔度差曲率具有良好的局部损伤识别能力, 受到的不确定影响较小, 损伤识别性能较稳定。

(3)基于模态柔度差曲率实现了异形桥梁单位置及多位置的损伤识别。

(4)遗传优化支持向量机方法能准确识别异形桥梁损伤程度。单位置损伤识别误差小于3%; 多位置损伤识别误差小于4.94%, 识别精度较高, 具备良好的损伤程度识别能力。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	杨秋伟, 刘济科. 工程结构损伤识别的柔度方法研究进展[J]. 振动与冲击, 2011, 30(12): 147-153. Yang Qiu-wei, Liu Ji-ke. Structural damage identification with flexibility changed: a review[J]. Journal of Vibration and Shock, 2011, 30(12): 147-153. [本文引用:1]
[2]	Chan T H T, Yu L, Tam H Y, et al. Fiber Bragg grating sensors for structural health monitoring of Tsing Ma bridge: background and experimental observation[J]. Engineering Structures, 2006, 28(5): 648-659. [本文引用:1]
[3]	Xia Y, Hao H. Statistical damage identification of structures with frequency changes[J]. Journal of Sound and Vibration, 2003, 263(4): 853-870. [本文引用:1]
[4]	曹晖, Michael I F. 基于模态柔度曲率的损伤检测方法[J]. 工程力学, 2006, 23(4): 33-38. Cao Hui, Michael I F. Nondestructive damage evaluation indicator based on modal flexibility curvature[J]. Engineering Mechanics, 2006, 23(4): 33-38. [本文引用:1]
[5]	Cao M, Qiao P. Novel Laplacian scheme and multiresolution modal curvatures for structural damage-identification[J]. Mechanical Systems and Signal Processing, 2009, 23(4): 1223-1242. [本文引用:1]
[6]	Jassim Z A, Ali N N, Mustapha F, et al. A review on the vibration analysis for a damage occurrence of a cantilever beam[J]. Engineering Failure Analysis, 2013, 31: 442-461. [本文引用:1]
[7]	Cao M, Radzieński M, Xu W, et al. Identification of multiple damage in beams based on robust curvature mode shapes[J]. Mechanical Systems and Signal Processing, 2014, 46(2): 468-480. [本文引用:1]
[8]	张军, 刘建勋, 徐进, 等. 结构损伤诊断的模态柔度差曲率法[J]. 工程力学, 2011, 28(12): 112-118. Zhang Jun, Liu Jian-xun, Xu Jin, et al. Structural damage detection based on change in curvature of flexibility[J]. Engineering Mechanics, 2011, 28(12): 112-118. [本文引用:1]
[9]	Guo H Y, Li Z L. Structural damage identification based on Bayesian theory and improved immune genetic algorithm[J]. Expert Systems with Applications, 2012, 39(7): 6426-6434. [本文引用:1]
[10]	孙宗光, 陈一飞, 石健, 等. 基于模型试验的悬索桥结构损伤识别研究[J]. 工程力学, 2014, 31(6): 132-138. Sun Zong-guang, Chen Yi-fei, Shi Jian, et al. Modal test study on damage identification for suspension bridges[J]. Engineering Mechanics, 2014, 31(6): 132-138. [本文引用:1]
[11]	刘寒冰, 焦峪波, 程永春, 等. 基于模态曲率理论及神经网络的简支梁桥损伤识别[J]. 吉林大学学报: 工学版, 2011, 41(4): 963-967. Liu Han-bing, Jiao Yu-bo, Cheng Yong-chun, et al. Damage identification for simply supported beam bridge based on modal curvature theory and neural network[J]. Journal of Jilin University (Engineering and Technology Edition), 2011, 41(4): 963-967. [本文引用:1]
[12]	代琨, 于宏毅, 仇文博, 等. 基于SVM的网络数据无监督特征选择算法[J]. 吉林大学学报: 工学版, 2015, 45(2): 576-583. Dai Kun, Yu Hong-yi, Qiu Wen-bo, et al. Unsupervised feature selection algorithm based on support vector machine for network data[J]. Journal of Jilin University (Engineering and Technology Edition), 2015, 45(2): 576-583. [本文引用:1]
[13]	Lu P Z, Xie X, Shao C Y. Experimental study and numerical analysis of a composite bridge structure[J]. Construction and Building Materials, 2012, 30: 695-705. [本文引用:1]

2011

0.0

. 2011, 30(12):147-153 DOI:doi:10.3969/j.issn.1000-3835.2011.12.029

Structural damage identification with flexibility changed:a review

工程结构损伤识别的柔度方法研究进展

Yang Qiu-wei , Liu Ji-ke.

杨秋伟, 刘济科

Structural damage identification using measured static or dynamic data has emerged as a new research area in civil, mechanical and aerospace engineering communities. A large number of approaches have been proposed for detecting structural damage in recent years. In these existing approaches, the flexibility-based method is one of the promising techniques since the flexibility can be constructed easily from the measured static or lower frequency modes and is very sensitive to structural damage. This paper presents a general summary and review of the flexibility-based damage identification methods in the past two decades. These flexibility-based techniques can be divided into six groups by the different calculation methods and data used. The basic idea of each group is briefly illustrated and the main formulas are given, respectively. The advantages and shortcomings of these approaches are also discussed and compared in detail. In the end, several key issues related to flexibility-based damage identification methods are emphasized and future study aspects are pointed out.

工程结构的损伤识别问题是目前的研究热点，近年来已提出许多种损伤识别方法。其中，柔度方法因计算简单实用性强而倍受人们关注。本文综述了近二十年来基于柔度变化的结构损伤识别方法，按照计算方法和采用数据的不同将柔度方法进行了分类和归纳，阐述了各类柔度方法的基本原理和主要的计算公式，并分析和比较了各类柔度方法的优点和不足之处。最后讨论了柔度方法尚存的未解决难题并对后继研究方向作了展望。

... 0 引言桥梁在车辆荷载、环境侵蚀及材料老化的作用下,结构损伤不断出现^[1] ...

2006

0.0

... 基于结构振动特性的损伤识别方法具有测试方便、精度高和易于获取等优点,在桥梁健康监测和损伤识别中得到了广泛的应用^[2] ...

2003

0.0

... 基于动力参数的损伤识别指标包括频率、振型、模态曲率、频响函数和模态柔度等^[3,4,5] ...

2006

0.0

. 2006, 23(4):33-38 DOI:doi:10.3969/j.issn.1000-4750.2006.04.007

Nondestructive damage evaluation indicator based on modal flexibility curvature

基于模态柔度曲率的损伤检测方法

Cao Hui , Michael I F.

曹晖

Due to the high sensitivity of the change in modal flexibility to structural damage, quite a few nondestructive damage evaluation indicators based on modal flexibility have been put forward. These indicators, such as the change in modal flexibility, modal flexibility index and the change in uniform load surface curvature, were used in some cases and proved to be valid to some extent. In this paper, a new indicator is constructed. Rather than using the change in modal flexibility, the change in curvature of modal flexibility is adopted and called the modal flexibility curvature (MFC). Although the change in uniform load surface curvature also uses curvature, it is different from MFC since it adds up the modal flexibility matrix rowwise and then calculates the change of curvature, while MFC computes the change of curvature columnwise in the modal flexibility matrix and chooses the maximum in each column. Two simulations, a simple beam and a four-span continuous beam, are utilized to verify the new indicator. Compared to the aforementioned indicators and modal curvature index, MFC is proved to be valid and efficient in various cases, and superior to the competitors.

由于模态柔度对结构损伤的高灵敏性,各种基于模态柔度的检测指标在结构无损探伤NDE(Nondestructive Damage Evaluation)中应用较多,如模态柔度差、模态柔度改变率和均匀荷载面曲率差等.这些指标经应用验证都具有一定的有效性.在此基础上,采用模态柔度曲率的改变构建一种新的指标,称为模态柔度曲率差(MFC).尽管均匀荷载面曲率差也采用曲率,但不同的是它先将模态柔度矩阵按行加起来,再求损伤前后的曲率差.而提出的模态柔度曲率差则按列计算损伤前后模态柔度矩阵的曲率差,然后挑选每列里面最大的值作为指标.采用一个简支梁和一个四跨连续梁为算例,考虑各种损伤情况,将该指标与模态柔度差、模态柔度改变率和均匀荷载面曲率差、以及振型曲率改变率等指标进行了比较,证明了模态柔度曲率差检测损伤的有效性和优越性.

... 基于动力参数的损伤识别指标包括频率、振型、模态曲率、频响函数和模态柔度等^[3,4,5] ...

2009

0.0

... 基于动力参数的损伤识别指标包括频率、振型、模态曲率、频响函数和模态柔度等^[3,4,5] ...

2013

0.0

... Jassim等^[6]采用频响参数和模态置信准则(Modal assurance criterion,MAC)进行了悬臂梁的损伤诊断和识别 ...

2014

0.0

... Cao等^[7]提出了改进的模态曲率指标,具有较好的抗噪能力,室内试验验证了对多位置损伤识别的有效性 ...

2011

0.0

. 2011, 28(12):112-118

Structural damage detection based on change in curvature of flexibility

结构损伤诊断的模态柔度差曲率法

Zhang Jun , Liu Jian-xun , Xu Jin

张军, 刘建勋, 徐进

In order to estimate the structural damage more accurately, a new indicator is developed to detect the damage of 2D structures, which is according to the changes in the curvature of flexibility before and after damage occurring. Numerical simulations on 2D structures are carried out for damage diagnosis with different types of indicator. Comparison between results from different indicators shows that the present indicator, with less working effort involved, generates the same value as that of the change in modal flexibility curvature. However, in 3D structures, some indicators may be missed. To deal with this problem, the sum of the change in flexibility curvatures is proposed as a diagnosis indicator. Examples of a 3D truss bridge and a plate structure show that the proposed indicator is effective in 3D structures.

为了使损伤更加明确显示,在求得结构损伤前后的模态柔度差之后,建立模态柔度差曲率作为二维结构的损伤指标来诊断损伤。考虑多种损伤情况,对二维结构进行了数值模拟,并用不同类型的指标进行了诊断。对比结果表明,该文指标与模态柔度曲率差指标所得结果基本上是相同的,且该文方法计算工作量要小。为了弥补利用模态柔度曲率差指标在诊断三维结构多处损伤时存在指标遗漏的现象,建立了模态柔度差曲率和作为三维结构损伤指标。三维桁架桥与板结构的算例表明,模态柔度差曲率和指标在三维结构的损伤诊断中比模态柔度差曲率指标效果好。综上所述,对于二维结构而言,损伤诊断指标为模态柔度差曲率；对于三维结构而言,损伤诊断指标为模态柔度差曲率和。

... 张军等^[8]采用模态柔度差曲率和进行三维结构损伤识别,克服了模态柔度差曲率指标的漏判现象 ...

2012

0.0

... Guo等^[9]提出了基于贝叶斯理论和免疫遗传算法的结构多位置损伤识别方法 ...

2014

0.0

. 2014, 31(6):132-138 DOI:doi:doi:10.6052/j.issn.1000-4750.2012.12.0980

Modal test study on damage identification for suspension bridges

基于模型试验的悬索桥结构损伤识别研究

Sun Zong-guang , Chen Yi-fei , Shi Jian

孙宗光, 陈一飞, 石健

通过整桥模型试验,探讨了悬索桥结构损伤识别方法。首先面向损伤识别研究设计制作了长10m的悬索桥试验模型,并通过模型误差分析建立了相应的高精度有限元模型。基于悬索桥结构健康监测和试验检测的主要常用参数以及这些参数对结构损伤的灵敏性和相关性研究,确定损伤识别策略。采用有限元模型模拟可能的损伤工况,从而生成BP网络的训练样本数据。再将试验模型作为"实际结构"通过损伤模拟试验生成网络测试数据。就试验模拟的损伤情况而言,对损伤位置的识别准确率达到了86%,相应的损伤程度识别精度也达到可接受程度。显示了该方法较好的应用前景,对基于监测系统的悬索桥健康状态识别与评价具有参考意义。

... 孙宗光等^[10]采用BP神经网络对悬索桥数值模型进行损伤预测,准确度达到86% ...

2011

0.0

. 2011, 41(4):963-967

Damage identification for simply supported beam bridge based on modal curvature theory and neural network

基于模态曲率理论及神经网络的简支梁桥损伤识别

Liu Han-bing , Jiao Yu-bo , Cheng Yong-chun

刘寒冰, 焦峪波, 程永春

A two-step method was proposed to identify the damage of the simply supported beam bridge with multiple girders. The method identifies the structure damage using the modal curvature difference and the neural network technique to avoid the disadvantages of each single method. A numerical example was provided for a simply supported T beam bridge with five girders to verify the feasibility of the method, and the results show that this two-step method is effective to locate damage and evaluate the damage degree.

针对多片简支梁桥损伤识别问题，提出了一种分步识别法。该方法综合运用模态曲率差及神经网络技术对结构损伤进行识别，能够有效地发挥两种方法的优点。最后以一座五片简支T梁桥为算例进行了数值模拟。模拟结果表明，该方法可以准确识别结构的损伤位置及损伤程度，是一种行之有效的简支梁桥损伤识别方法。

... 然而,总结现有研究成果发现:神经网络采用梯度下降算法,参数设置繁琐,收敛速度慢^[11] ...

2015

0.0

. 2015, 45(2):576-583 DOI:doi:10.13229/j.cnki.jdxbgxb201502035

Unsupervised feature selection algorithm based on support vector machine for network data

基于SVM的网络数据无监督特征选择算法

Dai Kun , Yu Hong-yi , Qiu Wen-bo

代琨, 于宏毅, 仇文博

摘　要：面向线性不可分的未知格式网络数据,提出了一种基于支持向量机的无监督特征选择算法。该算法通过非线性映射函数将不可分的网络数据映射到高维空间中,然后在高维空间中进行无监督的特征选择。该算法在特征选择之前不需要人工构造候选特征集合,直接从原始网络数据中自动地选择关键特征。利用人工数据集和网络数据集进行的实验结果表明：本文算法在特征选择可行性和有效性方面都有良好的表现。

... 支持向量机依赖部分关键数据,降低了模型的复杂程度,具有较好的预测能力^[12] ...

2012

0.0

... 1 异形桥梁概况选取典型异形桥梁为损伤识别研究对象^[13] ...