偏心荷载作用下单搭接胶接接头的应力分析

引用本文

李春良, 王方彦, 张立辉, 王静. 偏心荷载作用下单搭接胶接接头的应力分析. 吉林大学学报:工学版, 2016, 46(6): 1874-1880
LI Chun-liang, WANG Fang-yan, ZHANG Li-hui, WANG Jing. Stress analysis of adhesively bonded single lap joint under eccentric load. Journal of Jilin University Engineering and Technology Edition, 2016, 46(6): 1874-1880 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201606016
Permissions

偏心荷载作用下单搭接胶接接头的应力分析

李春良, 王方彦, 张立辉, 王静

吉林建筑大学交通科学与工程学院,长春 130118

王静(1980-),女,副教授,博士.研究方向:层状结构理论及应用.E-mail:wangjing@yahoo.com.cn

作者简介:李春良(1978-),男,教授,博士.研究方向:复合结构理论及应用.E-mail:lichli3300@163.com

基金项目:国家自然科学基金项目(51308256); 住房和城乡建设部项目(2014K1066); 吉林省教育厅“十二五”科技项目(2015265)

摘要

基于弹性力学理论建立了偏心荷载作用下板材类单搭接胶接接头界面粘结应力的计算模型,研究了偏心荷载作用下界面粘结剪应力随各粘结参数的变化规律,给出了单搭接胶接接头的定量设计公式,指出了各参数对界面粘结剪应力的影响程度。结果表明:偏心荷载作用时,界面粘结剪应力最大峰值位于粘结角处,该处最先发生破坏,可通过增加接头搭接宽度和搭接长度来抑制界面间粘结破坏的发生;并且剪应力会随着距离的增加呈现出非线性递减趋势;另外,在偏心荷载作用下,如果采用硬度较小的接头板材,会导致角点处产生较大的粘结应力。将这些规律和特点应用在实际工程中,可以避免单搭接胶接接头破坏。

关键词: 机械设计; 偏心荷载; 界面应力; 胶层; 单搭接接头

中图分类号:TQ436.2 文献标志码:A 文章编号:1671-5497(2016)06-1874-07

Stress analysis of adhesively bonded single lap joint under eccentric load

LI Chun-liang, WANG Fang-yan, ZHANG Li-hui, WANG Jing

School of Communication Science and Engineering, Jilin Jianzhu University, Changchun 130118,China

Abstract

Based on theory of elastic mechanics, the bonding stress model of adhesively bonded single lap joint under eccentric load was established. The effects of different parameters on the interfacial shear stress were investigated. A quantitative design formula of the single lap joint was given. The results show that the maximum shear stress is located at the bond corner, which will be first damaged. However, the bond failure can be avoided by increasing the width and length of the single lap joint. The shear stress decreases nonlinearly with the increase in distance. Besides, if the hardness of the overlap plate is lower, the bond stress at the corner will be higher under eccentric load. The results of this study provide a reference for engineering practice.

Key words: mechanical design; torsional loading; interfacial stress; adhesive layer; single lap joint

Show Figures

0 引言

胶接技术作为一种独特的结构连接技术^[1], 相比于机械连接具有连接效率高、应力分布均匀、工艺简单等优点^[2]。在实际工程中, 胶接搭接接头所承受的荷载大多都是偏心的, 其应力状态要比轴心荷载作用时复杂。目前关于偏心荷载作用下单搭接胶接接头的应力状态的研究成果并不多, 且大多数都是针对在轴向拉伸荷载作用下的情况。如Gunnion等^[3]研究了轴心荷载作用下斜搭接接头不同参量对胶层中应力分布的影响。Campilho等^[4]研究了轴心荷载作用下单面和双面搭接接头的受力情况。Kim等^[5]对轴心荷载作用下复合材料单搭接胶接接头的极限强度进行了预测。王中强等^[6]推导了轴心荷载作用下胶接界面应力模型和胶接件力学模型。李龙等^[7]对被粘接件为钢板和铝板的刚度平衡、非平衡搭接胶接接头进行了不同温度下的轴心拉伸载荷剪切强度试验。文献[8, 9]分析了搭接长度和搭接厚度对接头强度和破坏模式的影响。

由于胶接搭接接头承受的荷载大多都是偏心的, 轴心荷载作用下接头的理论成果不适用于偏心荷载作用下的情况。如何准确地计算和分析偏心荷载胶接接头的粘结应力问题对复合材料胶接技术的发展至关重要。

本文对偏心荷载作用下的单搭接胶头的偏心受力进行了研究, 指出了偏心荷载作用下单搭接胶接接头部位的应力分布规律、危险破坏点出现的位置及相关参数变化对胶接接头部位的应力分布规律的影响程度。本文建立的力学模型能够用于复合结构胶头设计和受力状态的安全监测。

1 偏心荷载作用下单搭接接头模型

1.1 计算模型和基本假设

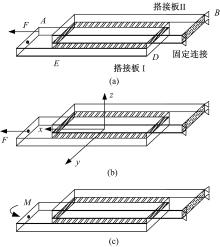
计算模型如图1(a)所示, 其中搭接板I在A角点处受偏心荷载F作用, 为了等效偏心力作用, 将F移动到搭接板端I截面的中心点处, 并施加绕中心点的xy面内弯矩M, 如图1(b)(c)所示。

	Figure Option View Download New Window
	图1 偏心荷载作用下的单搭接接头Fig.1 Single lap joint under eccentric tensile load

采用如下基本假设:①搭接接头不发生非xy平面外的绕转。②搭接板I和板II间的胶层只承受剪切力, 忽略其正应力的影响。③搭接板I和搭接板II内承受的正应力沿厚度方向均匀分布。④搭接板I的粘结区域绕粘结面的形心转动时, 搭接板上任意直线在转动后仍保持为直线, 即刚体位移。⑤胶粘层厚度较薄, 胶层破坏多为脆性瞬时破坏, 塑性过程非常短, 分析中假定胶粘层的本构关系为弹性关系。⑥单搭接胶接接头的粘结胶采用有机类胶脂。假定胶接接头受力工作条件是温度和湿度稳定的单一环境。

1.2 轴向拉伸荷载作用时胶接接头应力状态的模型

将图1(b)分解, 取受力单元如图2和图3所示。

	Figure Option View Download New Window
	图2 轴心荷载作用时搭接接头受力模型Fig.2 Mechanical model of lap joint under axial load

	Figure Option View Download New Window
	图3 微元段受力模型Fig.3 Mechanical model of infinitesimal section

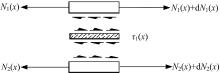
根据图3中搭接板I、II及胶层受力状态, 有:

$\begin{matrix} \begin{matrix} τ_{1} (x) = \frac{d N_{1} (x)}{dxb} (1) \\ d N_{1} (x) = d σ_{1} (x) bt (2) \end{matrix} \end{matrix}$

式中:τ ₁(x)为轴心力作用时接头界面间粘结剪应力; N₁(x)、N₂(x)分别为搭接板I、II受到的轴向力; b为粘结区域的宽度; t为搭接板厚度。

联立式(1)(2)导出式(3):

$\begin{matrix} τ_{1} (x) = \frac{d σ_{1} (x) t}{dx} \end{matrix}$ (3)

根据胶层变形规律, 建立胶层的剪应力计算公式:

$\begin{matrix} τ_{1} (x) = G \frac{u_{1} (x) - u_{2} (x)}{t_{a}} \end{matrix}$ (4)

式中:t_a、G分别为粘结胶层厚度和剪切模量; u₁(x)、u₂(x)分别为x位置处搭接板I和板II的纵向位移。

设在在荷载作用下, 位置点(x, y)处的位移为(u, v)。将式(4)代入式(3)导出式(5):

$\begin{matrix} \begin{matrix} \frac{d σ_{1} (x)}{dx} = \frac{τ_{1} (x)}{t} = \frac{G}{t t_{a}} [u_{1} (x) - u_{2} (x)] \\ (5) \end{matrix} \end{matrix}$

由式(5)建立如下方程:

$\begin{matrix} \begin{matrix} \frac{d^{2} σ_{1} (x)}{d x^{2}} = \frac{G}{t t_{a}} [\frac{d u_{1} (x)}{dx} - \frac{d u_{2} (x)}{dx}] = \\ \frac{G}{t t_{a}} [ε_{1} (x) - ε_{2} (x)] \end{matrix} \end{matrix}$ (6)

根据应力与应变的关系有:

$\begin{matrix} ε_{1} (x) = \frac{σ_{1} (x)}{E}; ε_{2} (x) = \frac{σ_{2} (x)}{E} \end{matrix}$

式中:E为搭接板的弹性模量。

因此式(6)整理为:

$\begin{matrix} \frac{d^{2} σ_{1} (x)}{d x^{2}} \end{matrix}$ = $\begin{matrix} \frac{G}{t_{a} t} \end{matrix} \begin{matrix} [\frac{σ_{1} (x) - σ_{2} (x)}{E}] \end{matrix}$

而根据力学关系有:

$\begin{matrix} σ_{2} (x) = \frac{F - N_{1} (x)}{bt} = \frac{F - σ_{1} (x) tb}{bt} \end{matrix}$ (7)

将式(7)代入式(6), 能够建立如下方程:

$\begin{matrix} \frac{d^{2} σ_{1} (x)}{d x^{2}} - \frac{2 G}{t t_{a} E} σ_{1} (x) + \frac{FG}{t^{2} t_{a} bE} = 0 \end{matrix}$ (8)

假设:

$\begin{matrix} \begin{matrix} A = \frac{2 G}{t t_{a} E} \\ B = \frac{G}{t^{2} t_{a} bE} \end{matrix} \end{matrix}$

则能够建立:

$\begin{matrix} \begin{matrix} σ_{1} (x) = F (C_{1} e^{\sqrt[]{A} x} + C_{2} e^{- \sqrt[]{A} x} + \frac{B}{A}) (9) \\ τ_{1} (x) = F (C_{1} \sqrt[]{A} e^{\sqrt[]{A} x} - C_{2} \sqrt[]{A} e^{- \sqrt[]{A} x}) t (10) \end{matrix} \end{matrix}$

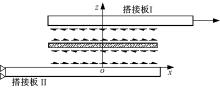
根据图2, 可以建立如下边界条件:

$\begin{matrix} \{\begin{matrix} x = \frac{l}{2}, σ_{1} (\frac{l}{2}) = \frac{F}{bt} \\ x = - \frac{l}{2}, σ_{1} (l) = 0 \end{matrix} \end{matrix}$

式中:l为粘结区域长度。

因此可以求得系数C₁、C₂为:

$\begin{matrix} \{\begin{matrix} C_{1} = \frac{e^{\frac{\sqrt[]{A} l}{2}} (Bbt - A) - e^{\frac{- \sqrt[]{A} l}{2}} Bbt}{Abt (e^{- \sqrt[]{A} l} - e^{\sqrt[]{A} l})} \\ C_{2} = \frac{e^{\frac{- \sqrt[]{A} l}{2}} (A - Bbt) + e^{\frac{\sqrt[]{A} l}{2}} Bbt}{Abt (e^{- \sqrt[]{A} l} - e^{\sqrt[]{A} l})} \end{matrix} \end{matrix}$

1.3 xy面内弯矩作用时胶接接头应力状态的模型

将图1(c)分解为搭接板I、II、粘结胶层三部分, 各自受力状态如图4所示。

	Figure Option View Download New Window
	图4 面内弯矩作用时接头受力模型Fig.4 Mechanical model of lap joint in-plane bending moment

在图4中, 根据假设可知, 搭接板I上任意直线在转动后仍保持为直线, 粘结面上任意点(x, y)处的剪应力、剪应变均与粘结界面形心o的距离成正比, 因此有:

$\begin{matrix} τ_{2} (x, y) = K \sqrt[]{x^{2} + y^{2}} \end{matrix}$ (11)

式中:K为剪应力面内扭转系数。

根据搭接板I上作用的面内弯矩情况, 利用弯矩平衡条件可以建立以下平衡方程:

$\begin{matrix} M = \int_{-l/2}^{l/2} \int_{-b/2}^{b/2} \sqrt[]{x^{2} + y^{2}} τ_{2} (x, y) dxdy = \frac{Kbl (l^{2} + b^{2})}{12} \end{matrix}$ (12)

将式(11)代入式(12), 得到面内扭转系数为:

$\begin{matrix} K = \frac{12 M}{bl (l^{2} + b^{2})} = \frac{12 F e_{0}}{bl (l^{2} + b^{2})} \end{matrix}$

式中:e₀为偏心距离。

点(x, y)处面内扭转剪应力为:

$\begin{matrix} τ_{2} (x, y) = \frac{12 F e_{0} \sqrt[]{x^{2} + y^{2}}}{bl (l^{2} + b^{2})} \end{matrix}$ (13)

1.4 偏心荷载作用时胶头的总剪应力状态模型

在1.2、1.3节中分别建立了图1(b)(c)两种状态的胶层接头界面粘结应力的力学模型, 因此在偏心荷载作用下, 接头内任意点的粘结应力力学模型为:

$\begin{matrix} \begin{matrix} τ_{总} (x, y) = F {A t^{2} (C_{1}^{2} e^{2 \sqrt[]{A} x} - 2 C_{1} C_{2} + C_{2}^{2} e^{- 2 \sqrt[]{A} x}) + \frac{144 e_{0}^{2} (x^{2} + y^{2})}{b^{2} l^{2} (l^{2} + b^{2})^{2}} + \\ [24 \sqrt[]{A} t (C_{1} e^{\sqrt[]{A} x} - C_{2} e^{- \sqrt[]{A} x}) e_{0} \sqrt[]{x^{2} + y^{2}} cosα] \times [bl (l^{2} + b^{2} {)]}^{- 1}}^{\frac{1}{2}} (14) \end{matrix} \end{matrix}$

方向: tan(α )= $\begin{matrix} \frac{12 e_{0} \sqrt[]{x^{2} + y^{2}}}{bl (l^{2} + b^{2})} \times / \end{matrix}$ (C₁ $\begin{matrix} \sqrt[]{A} \end{matrix} \begin{matrix} e^{\sqrt[]{A} x} \end{matrix}$ -C₂ $\begin{matrix} \sqrt[]{A} \end{matrix} \begin{matrix} e^{- \sqrt[]{A} x} \end{matrix}$ )t]^-¹

式中:α 为粘结界面(x, y)处τ ₁(x, y)与τ ₂(x, y)之间的夹角。

1.5 单搭接胶接接头承载能力定量计算公式

在设计单搭接胶接接头时, 需计算出胶接接头所能承受的极限承载力F的定量值。根据后文粘结应力分布规律可知, 单搭接胶接接头的薄弱部位为搭接接头的角点位置处的粘结界面点处, 因此在计算接头的极限承载能力时, 以该处界面间粘结应力极限值[τ ]为控制条件, 即:

$\begin{matrix} τ_{总} (\frac{l}{2}, \frac{b}{2}) \leq [τ] (15) \end{matrix}$

将式(14)代入式(15)中, 最终可推导出单搭接胶接接头承载能力定量公式为:

$\begin{matrix} \begin{matrix} F \leq [τ] \\ [A t^{2} (C_{1}^{2} e^{l \sqrt[]{A} x} - 2 C_{1} C_{2} + C_{2}^{2} e^{- l \sqrt[]{A}}) + \frac{9}{l^{2} (l^{2} + b^{2})} + \\ {\frac{6 \sqrt[]{A} tb (C_{1} e^{\frac{l \sqrt[]{A}}{2}} - C_{2} e^{- \frac{l \sqrt[]{A}}{2}})}{l (l^{2} + b^{2})}]}^{- \frac{1}{2}} (16) \end{matrix} \end{matrix}$

式中:[τ ]为单接接头界面粘结应力极限强度值。

如果已知搭接接头部分的相关参数值, 则根据式(16)可计算出接头所能承受的破坏荷载值。

2 算例及参数分析

2.1 算例

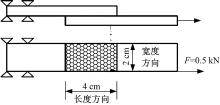
选取算例, 其中搭接板厚度为5 mm。板材弹性模量E为2.0× 10¹¹ MPa, 胶层按弹性材料处理, 其剪切模量G为2.1× 10⁹ MPa, 搭接板材结构尺寸如图5所示。

	Figure Option View Download New Window
	图5 算例图示Fig.5 Example figure

	Figure Option View Download New Window
	图6 剪应力曲线Fig.6 Shear stress curve

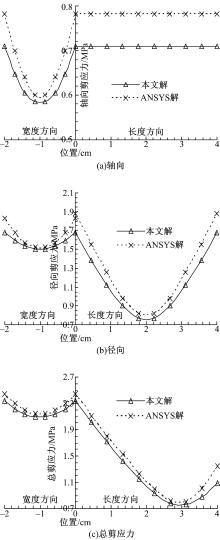
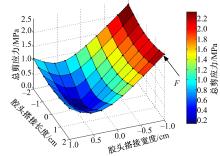
偏心荷载作用时的粘结应力曲线见图6, 根据图6对比曲线发现:解析结果与ANSYS结果吻合, 并且计算规律性一致, 表明本文建立的理论计算模型是正确的, 可以用本文的计算模型来分析实际工程中偏心荷载作用下单搭接接头粘结界面应力问题。另外, 根据图6可以发现:不论是轴向剪应力、径向剪应力还是总剪应力, 在单搭接胶头粘结边缘处的剪应力值均为最大。因此在偏心荷载作用下, 搭接接头的粘结界面的边缘角点处最容易先破坏。图7为三维空间粘结界面剪应力图, 从图7可以更清楚地观察出在F受力点处粘结界面间的总剪应力最大。

	Figure Option View Download New Window
	图7 总剪应力三维曲线图Fig.7 Three-dimension graph of total shear stress

2.2 相关参数分析

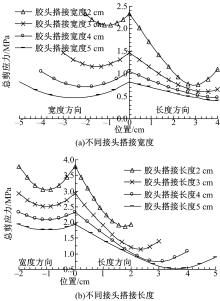
(1)搭接宽度、长度不同时剪应力对比

图8为偏心荷载作用时不同接头搭接宽度和搭接长度时粘结界面剪应力对比曲线, 观察发现:随着搭接宽度或搭接长度的增加, 在接头搭接长度、搭接宽度方向, 总剪应力均会降低。因此在实际工程中, 增加粘结接头宽度或搭接长度, 对于减小粘结区域的剪应力具有一定的意义。

	Figure Option View Download New Window
	图8 不同接头搭接宽度和长度时总剪应力曲线Fig.8 Total shear stress of different lap joint width and length

(2)接头胶层厚度不同时剪应力对比

图9为偏心荷载作用下, 接头胶层粘结厚度不同时的粘结界面剪应力对比曲线, 观察发现:增加胶层粘结厚度对减小粘结区域的剪应力效果不明显。

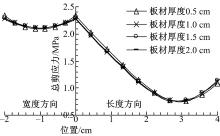
	Figure Option View Download New Window
	图9 不同接头胶层厚度时总剪应力曲线Fig.9 Total shear stress of different adhesive thickness

(3)搭接板材厚度不同时剪应力对比

图10为偏心荷载作用下, 搭接板材厚度不同时的粘结界面剪应力对比曲线, 观察发现:增加板材厚度时对减小粘结区域的剪应力效果不明显。

	Figure Option View Download New Window
	图10 不同搭接板材厚度时总剪应力曲线Fig.10 Total shear stress of different sheet thickness

(4)板材弹性模量不同时剪应力对比

图11为偏心荷载作用下, 板材弹性模量不同时粘结界面剪应力对比曲线, 观察发现:当板材弹性模量降低幅度较大时, 搭接板材的角点位置处的粘结应力迅速变大, 所以在实际工程中, 如果板材较软, 搭接接头间的粘结剪应力会较大。

	Figure Option View Download New Window
	图11 搭接板材不同弹性模量时总剪应力曲线Fig.11 Total shear stress of different Elastic Modulus

	Figure Option View Download New Window
	图12 不同偏心距时总剪应力曲线Fig.12 Total shear stress of different eccentricity

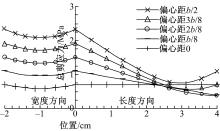
(5)偏心距不同时剪应力对比

图12为偏心距不同时板材角点处粘结界面剪应力对比曲线, 观察发现:当偏心距逐渐变大时, 搭接板材的角点位置处的胶层粘结应力迅速变大, 所以如果偏心距越大则角点处越容易发生破坏。

(6)各参数变化时剪应力变化规律

图13为各参数变化时, 搭接接头粘结界面间最大剪应力随参数的变化规律, 根据图13可以更直观地观察到改变各参数对界面粘结剪应力影响情况的强弱关系。其中改变搭接接头的搭接宽度和搭接长度对于降低粘结界面间的最大剪应力具有明显的意义, 而改变胶层厚度和搭接板材厚度对于改变粘结界面间的剪应力效果不明显。这些规律可以应用于实际工程中。

	Figure Option View Download New Window
	图13 各参数变化对界面最大总剪应力的影响Fig.13 Influence law of total shear stress by different parameters

3 结论

建立了偏心荷载作用下, 板材类单搭接接头粘结界面间剪应力的计算模型, 并对各参数变化对界面粘结剪应力的影响规律进行了计算对比分析, 有以下结论:

(1)偏心荷载作用时, 界面粘结剪应力最大值位于粘结角点处, 并且剪应力随着距离的增加呈现出非线性递减趋势, 当距离超过一定长度后, 粘结剪应力值降为很小。因此在偏心荷载作用下, 搭接接头的粘结界面的边缘角点处最容易先发生破坏。

(2)增加接头搭接宽度和搭接长度, 可以降低界面间粘结剪应力峰值。

(3)在工程中, 当偏心荷载作用时, 如果采用的板材硬度较小, 搭接板材的角点位置处的粘结应力会很大, 所以在实际工程中, 如果板材较软时, 搭接接头更容易发生破坏。此规律应加以重视, 避免在实际工程中引起胶层的负载增大。

(4)本文在建模过程中假设胶接接头受力工作条件是稳定的单一环境, 其中环境温度为25 ℃、相对湿度为50%, 对于短期是可行的。但对在长期处于复杂环境中的粘胶层, 在时间、温度、紫外线作用下会发生老化现象, 可根据外界环境劣化程度, 将胶粘层的剪切模量和剪切强度值乘以环境影响后劣化参数进行降低, 然后再根据文中给出的公式进行计算。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	王玉奇, 何晓聪, 周森. 高温对单搭接接头强度的影响[J]. 宇航材料工艺, 2014(2): 78-82. Wang Yu-qi, He Xiao-cong, Zhou Sen. Influences of high temperature on strength of adhesively bonded single lap joints[J]. Aerospace Materials & Technology, 2014(2): 78-82. [本文引用:1]
[2]	刘伟先, 周光明, 王新峰. 基于渐进损伤模型的复合材料斜接接头的拉伸强度[J]. 材料科学与工程学报, 2012, 30(5): 665-671. Liu Wei-xian, Zhou Guang-ming, Wang Xin-feng. Parametric study on the tensile strength of the composites'scarf joint using progressive damage model[J]. Journal of Materials Science &Engineering, 2012, 30(5): 665-671. [本文引用:1]
[3]	Gunnion A J, Herszberg I. Parametric study of scarf joints in composite structures[J]. Composite Structures, 2006, 75(1-4): 364-376. [本文引用:1]
[4]	Campilho R, de Moura M S S F, Domingues J J M S. Modeling single and double-lap repairs on composite materials[J]. Composites Science and Technology, 2005, 65(13): 1948-1958. [本文引用:1]
[5]	Kim K S, Yi Y M, Cho G R. Failure prediction and strength improvement of unidirectional composite single lap bonded joints[J]. Composite Structures, 2008, 82(4): 513-520. [本文引用:1]
[6]	王中强, 张开富, 李原, 等. CFRP/Al复合构件胶接界面力学建模与强度分析[J]. 西北工业大学学报, 2010, 28(6): 858-865. Wang Zhong-qiang, Zhang Kai-fu, Li Yuan, et al. An interface stress model for strength analysis of CFRP/Al(carbon fiber reinforced plastic/aluminum) composite component[J]. Journal of North Western Poly Technical University, 2010, 28(6): 858-865. [本文引用:1]
[7]	李龙, 胡平, 刘立忠. 刚度不平衡单搭接胶接接头剪切试验与强度分析[J]. 农业机械学报, 2011, 42(1): 213-217. Li Long, Hu Ping, Liu Li-zhong. Strength of unsymmetric single-lap adhesively bond joints[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(1): 213-217. [本文引用:1]
[8]	郭霞, 关志东, 刘遂, 等. 搭接长度对复合材料单搭接胶接接头的影响[J]. 科技导报, 2013, 31(7): 37-41. Guo Xia, Guan Zhi-dong, Liu Sui, et al. Effect of lap length on the adhesive-bonded single-lap composite joints[J]. Science Technology Review, 2013, 31(7): 37-41. [本文引用:1]
[9]	石小红, 陈海立, 周光明. 基于渐进损伤模型的双搭接对接接头弯曲性能[J]. 南京理工大学学报, 2014, 38(4): 464-469. Shi Xiao-hong, Chen Hai-li, Zhou Guang-ming. Bending of bilateral butt joints using progressive damage model[J]. Journal of Nanjing University of Science and Technology, 2014, 38(4): 464-469. [本文引用:1]

0.0

... 0 引言胶接技术作为一种独特的结构连接技术^[1],相比于机械连接具有连接效率高、应力分布均匀、工艺简单等优点^[2] ...

2012

0.0

. 2012, 30(5):665-671

Parametric study on the tensile strength of the composites'scarf joint using progressive damage model

基于渐进损伤模型的复合材料斜接接头的拉伸强度

Liu Wei-xian , Zhou Guang-ming , Wang Xin-feng.

刘伟先, 周光明, 王新峰

摘　要：本文首先以斜接角度、搭接长度以及搭接厚度为参数分别建立了复合材料单边斜接接头和双边斜接接头在拉伸载荷下的参数化有限元模型,采用abaqus软件中UMAT子程序功能编写了材料损伤本构模型,并利用cohesive单元模拟胶接界面损伤。通过渐进损伤分析,模拟出斜接接头的三种破坏模式,最终得到了各参数变化对斜接接头拉伸强度的影响,其中母板最终破坏模式对应最大拉伸强度,并对单边斜接接头和双边斜接接头结果进行了对比分析,得出双边斜接接头强度大于单边斜接接头强度的结论。

... 0 引言胶接技术作为一种独特的结构连接技术^[1],相比于机械连接具有连接效率高、应力分布均匀、工艺简单等优点^[2] ...

2006

0.0

... 如Gunnion等^[3]研究了轴心荷载作用下斜搭接接头不同参量对胶层中应力分布的影响 ...

2005

0.0

... Campilho等^[4]研究了轴心荷载作用下单面和双面搭接接头的受力情况 ...

2008

0.0

... Kim等^[5]对轴心荷载作用下复合材料单搭接胶接接头的极限强度进行了预测 ...

2010

0.0

. 2010, 28(6):858-865 DOI:doi:10.3969/j.issn.1000-2758.2010.06.010

An interface stress model for strength analysis of CFRP/Al(carbon fiber reinforced plastic/aluminum) composite component

CFRP/Al复合构件胶接界面力学建模与强度分析

Wang Zhong-qiang , Zhang Kai-fu , Li Yuan

王中强, 张开富, 李原

文章以CFRP板/Al合金板复合构件的胶接接头为研究对象,通过以胶接界面为纽带,使用复合材料层合板理论、胶接接头平衡方程和控制方程,同时考虑偏心拉伸单搭接接头,造成弯矩对胶接接头的影响,推导出胶接界面应力模型和胶接件力学模型.并使理论模型满足搭接区域端头处胶层剪应力为零等所有边界条件.通过理论模型的解与三维有限元分析结果对比,证明理论模型的正确性.

... 王中强等^[6]推导了轴心荷载作用下胶接界面应力模型和胶接件力学模型 ...

2011

0.0

. 2011, 42(1):213-217

Strength of unsymmetric single-lap adhesively bond joints

刚度不平衡单搭接胶接接头剪切试验与强度分析

Li Long , Hu Ping , Liu Li-zhong.

李龙, 胡平, 刘立忠

... 李龙等^[7]对被粘接件为钢板和铝板的刚度平衡、非平衡搭接胶接接头进行了不同温度下的轴心拉伸载荷剪切强度试验 ...

2013

0.0

. 2013, 31(7):37-41 DOI:10.3981/j.issn.1000-7857.2013.07.005

Effect of lap length on the adhesive-bonded single-lap composite joints

搭接长度对复合材料单搭接胶接接头的影响

Guo Xia , Guan Zhi-dong , Liu Sui

郭霞, 关志东, 刘遂

1. School of Aeronautic Science and Engineering, Beihang University, Beijing 100191, China;2. Shanghai Aircraft Manufacturing CO., Ltd., Commercial Aircraft Corporation of China, Ltd., Shanghai 200436, China

The tensile performance of the adhesive-bonded single-lap composite joints is studied by the finite element modeling. The effect of the lap length on the tensile properties is analyzed with respect to the stress distribution and the failure mode. It is shown that: when the lap length changes from 5mm to 45mm, the minimum shear stress gradually decreases; when the lap length is greater than 20mm, the effect of the lap length on the stress distribution is decreased; the failure load increases gradually with the lap length; the increase rate is reduced when the lap length is greater than 20mm; the failure mode of a single lap joint is to start from the edge of the adhesive -composite interface, and then the adhesive damage. The lap length affects the damage level.

针对复合材料单搭接接头的拉伸性能进行有限元建模,分析搭接长度对单搭接接头的应力分布和破坏模式的影响.结果表明:当搭接长度在5～45mm变化时,最小剪切应力逐渐减小,当搭接长度大于20mm时,搭接长度对应力分布的影响减少;破坏载荷逐渐增大,当搭接长度大于20mm时,搭接长度对破坏载荷的影响减少;单搭接接头的破坏模式为胶层-复合材料界面的边缘发生部分损伤,导致胶层损伤,搭接长度的变化影响单搭接接头的损伤严重程度.

2014

0.0

. 2014, 38(4):464-469 DOI:doi:10.3969/j.issn.1005-9830.2014.04.005

Bending of bilateral butt joints using progressive damage model

基于渐进损伤模型的双搭接对接接头弯曲性能

Shi Xiao-hong , Chen Hai-li , Zhou Guang-ming.

石小红, 陈海立, 周光明

为研究复合材料双搭接连接的搭接长度和搭接厚度对于对接接头弯曲强度的影响，使用ABAQUS进行了渐进损伤分析。该分析理论基于三维渐进损伤分析方法和粘聚区模型，并通过用户子程序编写的复合材料本构和 Cohesive Contact来模拟复材损伤和胶接界面损伤。通过渐进损伤分析，得到不同搭接参数下接头的损伤过程和弯曲强度。结果表明：随着搭接长度的增加，接头强度先增大后趋于稳定，而随着搭接厚度的增加，接头强度先增大后减小。该文研究成果可为复合材料连接的承弯设计提供参考。