作者简介:欧阳天成(1986-),男,博士研究生.研究方向:机械系统动力学.E-mail:ouyangtiancheng@163.com
为了解决具有旋转和轴向2个方向速度的胶印机窜墨辊渐开线圆柱直齿轮的润滑问题,构建了一种基于有限长线接触的混合弹性流体动压润滑模型,对不同粗糙面类型的齿轮润滑进行数值模拟。在几何分析基础上,根据混合弹流理论建立了齿轮系统的控制方程。对控制方程进行无量纲化和离散化后,采用高效的多重网格算法进行数值求解,获得了不同速度比、粗糙面类型的油膜压力分布、膜厚分布、综合摩擦因数和粗糙面承载率。研究结果表明:直齿轮的轴向速度加剧了齿端的应力集中;粗糙面类型对齿轮润滑有重要影响;没有轴向速度时,纵向粗糙面的齿端压力最大,达到593.1 MPa,有轴向速度时,纵向粗糙面的压力升高值最小,只有188.7 MPa;同时发现,轴向速度和粗糙面类型都对摩擦因数有影响。
A new model of involute spur gear of form inking roller of offset press that contains rotational and axial velocities is proposed to study the lubrication behaviour. The model is based on the finite line-contact mixed Elastohydrodynamic Lubrication (EHL) formulas, which is capable of handling the numerical simulation gear lubrication with different rough surface patterns. On the basis of geometric analysis, the governing equations are built up with the help of the mixed EHL theory. Then, the efficient multigrid method is applied to solve the governing equations after the nondimensionalization and discretization. As results, the numerical simulations can accurately predict the film pressure distribution, the film thickness distribution, the compositive friction coefficient and the asperity load ratio. It is shown that the axial velocity of spur gear intensifies the stress concentration on the gear tip. Different rough surface patterns obviously influence the lubrication behaviour of the spur gear. The film pressure of longitudinally oriented surface reaches a maximum of 593.1 MPa under the condition of non-axial velocity. The rise of the film pressure of longitudinally oriented surface reaches a minimum of 188.7 MPa only under the condition that the axial velocity is not zero. It is also shown that both the axial velocity and the rough surface pattern obviously influence the friction coefficient.
齿轮传动机构的传递效率和可靠性与齿面润滑状况紧密相关, 特别是刮齿、点蚀和胶合等不良现象引起了众多学者的关注[1, 2, 3]。传统的齿面接触分析是基于半弹空间和光滑接触假设的Hertz接触理论, 由于其忽略了油膜效应和齿面粗糙类型, 造成分析结果与试验测量值差距甚大。随着计算机硬件、软件技术和数值算法的不断发展, 考虑齿面粗糙度的混合弹性流体动压润滑成为当今研究齿面接触的热点技术[4, 5]。
Dowson等[6]通过对大量的数值计算结果进行回归分析, 提出了无限长线接触膜厚公式。由于他们经验公式计算的膜厚与试验测量的膜厚基本吻合, 因此该方法在当今工程弹流润滑上得到广泛推广。Li等[7]运用混合弹流理论研究了直齿轮啮合过程的润滑特性, 结果显示, 载荷的突变会造成膜厚和压力的剧烈波动。Xu等[8]在混合弹流基础上分别建立起齿轮接触、摩擦和机械效率模型, 最后通过试验验证了数值算法的准确性。Zhu等[9]基于混合弹流理论研究了粗糙度对油膜特性的影响, 并且分析了几种典型齿面粗糙类型与膜厚之间的关系。Wang等[10]研究了不同加工粗糙度对滑动和滚动接触的影响。
以往对直齿轮弹流润滑的研究基本上采用一维线接触模型, 原因是直齿轮通常只有一个旋转方向运动且其齿宽方向的接触特性基本一致, 这种简化模型在一定范围内有相当的可行性。胶印机窜墨辊直齿轮不仅有传递动力的旋转运动, 还有实现均墨作用的轴向往复运动, 传统的一维线接触模型不再适用, 同时, 一维模型不能反映出不同类型粗糙齿面的纹理特征。因此, 本文提出一种具有2个方向速度的二维有限长线接触模型来研究窜墨辊直齿轮混合弹流润滑问题。
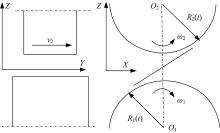
如图1所示, 渐开线直齿轮沿着啮合线上的运动可以用2个时变曲率半径的圆柱体接触来模拟, 主动轮无轴向速度, 从动轮的轴向往复速度为v2。啮合线上任意啮合点的等效曲率半径为:
式中:R、R1(t)、R2(t)分别为等效曲率半径、主动轮曲率半径和从动轮曲率半径; r1、r2分别为主、从动齿轮分度圆半径; α n、ζ 分别为压力角和啮合点到节点的距离, ζ ∈ [-l1, l2], l1和l2的计算公式为:
式中:ha1和ha2分别为主、从动齿轮齿顶高。
任意啮合点处的卷吸速度为:
式中:u、v分别为啮合点处x和y方向的润滑卷吸速度; ω 1为主动轮转速; i为传动比; u1、u2分别为主、从动轮沿x方向的润滑卷吸速度; v1、v2分别为主、从动轮沿y方向的润滑卷吸速度。
设润滑油为牛顿流体, 油膜压力沿膜厚方向保持不变, 忽略温度变化, 稳态状况下有2个方向速度的直齿轮Reynolds方程[11]为:
式中:ρ 、η 、h和p分别为润滑油密度、黏度、油膜厚度和油膜压力。
Reynolds方程边界条件为:
式中:xin、xout分别为计算区域的入口、出口位置; yl为齿轮端面的坐标。
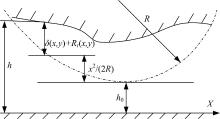
如图2所示, 油膜厚度h由刚体中心膜厚h0、几何膜厚x2/(2R)、弹性变形δ (x, y)和综合齿面粗糙度Rr(x, y)组成。
h=h0+x2/(2R)+δ (x, y)+Rr(x, y) (6)
δ (x, y)=
式中:E、Ω 分别为综合弹性模量和计算区域。
采用Roelands[11]公式计算黏度-压力方程和密度-压力方程分别为:
式中:ρ 0、η 0分别为环境压力温度下的密度和黏度; B1、B2、z分别为黏度-压力计算系数; A1、A2分别为密度-压力计算系数。
本次研究取三种典型的齿面粗糙类型作为混合弹流研究对象, 分别是随机粗糙表面(γ =1)、纵向粗糙表面(γ > 1)和横向粗糙表面(γ < 1), γ 为表面类型参数, 三种类型粗糙表面如图3所示。齿轮沿着啮合线接触过程中, 采用AGMA[12]推荐的方式加载, 外载荷由润滑油膜与接触粗糙面峰点共同承担, 其平衡方程为:
式中:Fp和Fr分别为油膜载荷和粗糙面峰点载荷; La为粗糙面峰点承载率。
粗糙面峰点承载率计算公式[13]如下:
式中:σ 、hd、α 分别为粗糙面算数平均偏差、维克斯硬度和当量黏度-压力系数; K为承载率修正系数。
承载率修正系数跟Masjedi[13]最小膜厚与粗糙面算数平均偏差之比、粗糙面类型关联, 其计算公式如下:
式中:Λ 为膜厚参数, Λ =hmin/Rr。
根据以前的研究结果发现, 使用牛顿流体计算得到的压力与膜厚分布和实际测量值误差不大, 但在摩擦力的计算上偏差却很大, 本文将采用Ree-Eyring[14]型非牛顿流体来计算齿面摩擦力, 从而得到摩擦因数。粗糙齿面的综合摩擦因数μ f的计算公式为:
式中:μ p、μ r、μ g分别为油膜摩擦因数、边界润滑摩擦因数和粗糙面峰点干摩擦因数(μ g=0.13)。
在弹性流体计算中, 通常需要将控制方程进行无量纲化, 将相关的物理量减少为几个无量纲参数进而缩减变量数目, 使方程得到简化。简化后的控制方程在求解效率和收敛性上都有很大提高。本文研究根据文献[14]进行控制方程的无量纲化。
应用中心与向后差分法分别对无量纲化后的Reynolds方程、油膜厚度方程、黏度-压力方程和载荷平衡方程等进行离散化, 以便进行数值求解。在计算区域内进行网格划分, x与y方向的节点数为129× 257[14]。
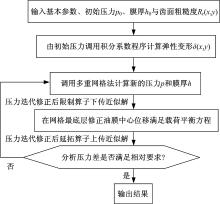
多重网格法被证明是求解大型非线性方程组的高效算法, 其求解思想是:对同一数学模型, 设置为几个层次, 对不同层次进行不同网格密度的划分, 轮流在稠密和稀疏网格上进行迭代, 以实现快速收敛于精确解的目的。本文将模型划分为4层网格, 顶层网格x和y方向的节点数为129× 257, 下层网格x和y方向的节点数分别是上层的一半, 计算流程如图4所示。首先在顶层进行迭代, 得到一组近似解; 然后依靠限制算子把近似解转移到下一层进行迭代, 在最底层通过修正油膜中心位移以满足载荷平衡条件; 之后利用延拓算子从下层把近似解转移到上层, 如果顶层近似解没有达到求解精度, 重复以上步骤, 直到收敛。
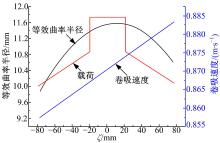
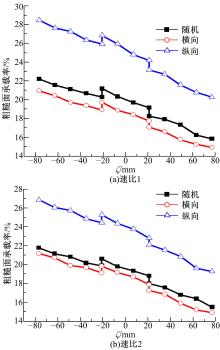
胶印机窜墨辊直齿轮的设计参数为:模数mn=3 mm; 齿数Z1、Z2分别为43和47; 齿宽B1、B2分别为120、30 mm; 外载荷F=900 N; 压力角为20° ; 综合齿面粗糙度算数平均偏差为0.4 μ m。图5是主动轮输入转速为375 r/min时, 外载荷、等效曲率半径和油膜卷吸速度沿啮合线上的变化曲线。轴向速度对直齿轮的润滑特性有一定的影响, 特别是在不同类型粗糙齿面下, 因此有必要研究轴向速度效应。本次研究取随机粗糙表面(γ =1)、纵向粗糙表面(γ =1.5)和横向粗糙表面(γ =0.5)为研究对象。齿轮旋转速度与轴向速度的两种极限比例分别是:速比1(1∶ 0)和速比2(1∶ 0.16)。通过数值计算得到两种速比下不同类型粗糙面的承载率, 如图6所示。
从图6(a)可以看出:没有轴向速度时, 纵向粗糙面的承载率最大而横向粗糙面的承载率最小, 随机粗糙面居中, 它们都是沿着啮合线呈下降趋势。产生这种现象的原因是:纵向粗糙面的纹理方向与油膜的卷吸速度平行, 导致排水现象发生, 油膜厚度下降从而使得更多的粗糙面峰点承担载荷; 横向粗糙面的纹理方向与油膜的卷吸速度垂直, 产生了泵效应, 油膜厚度增加而承载率下降; 沿着啮合线方向, 由于油膜卷吸速度的增大导致膜厚变大, 从而引起粗糙面承载率下降。
通过对比图6(a)和图6(b)可以发现, 有轴向速度时的纵向粗糙面承载率要小于无轴向速度时, 而横向粗糙面承载率却略有上升。原因是轴向速度分别导致了纵向、横向粗糙面的“ 泵” 和“ 排水” 效应。轴向速度也使得随机粗糙面的承载率微微下降但不明显, 原因是轴向速度远远小于旋转速度。
图7(a)和7(b)分别是速比1和2下纵向粗糙面的油膜压力分布。从图7(a)可以看出, 齿宽两端的压力明显高于中间, 产生了端泄效应, 并且在出口区出现二次压力峰。通过对比图7(a)和图7(b)可以发现:轴向速度的存在增强了齿宽一端的端泄效应, 使最大压力从593.1 MPa升高到781.8 MPa, 另一端的压力却有所下降。
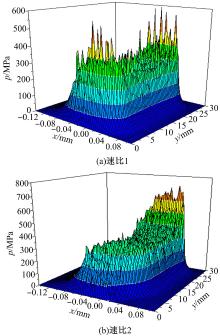 | 图7 不同速比下纵向粗糙面油膜压力分布Fig.7 Film pressure distribution of longitudinal rough surface under different speed ratio |
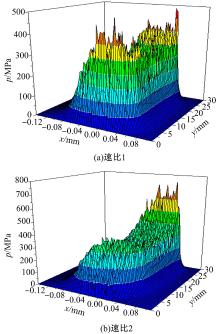 | 图8 不同速比下横向粗糙面油膜压力分布Fig.8 Film pressure distribution of transverse rough surface under different speed ratio |
图8(a)和8(b)分别为速比1和2下横向粗糙面的油膜压力分布。通过图8(a)可以看出, 齿宽两端产生了端泄效应。通过对比发现, 在2种速比下, 横向粗糙面的最大压力都要小于纵向粗糙面的最大压力。
表1给出了三种类型粗糙面在2种速比下的最大压力和最小油膜厚度。可以看出, 在没有轴向速度情况下, 横向粗糙面的压力最小(477.1 MPa), 而纵向粗糙面的压力最大(593.1 MPa)。2种速比下, 横向粗糙面的压力升高值最大(247.2 MPa), 而纵向粗糙面的压力升高值最小(188.7 MPa), 这表明了轴向速度对横向粗糙面的影响最大, 而对纵向粗糙面的影响最小, 随机粗糙面居中。轴向速度使得横向粗糙面的油膜厚度减小了0.015 μ m, 而其他两种粗糙面分别增大了0.012 μ m、0.021 μ m。因此, 对于有轴向速度的直齿轮, 要考虑轴向速度对不同类型粗糙面的应力集中效应。
| 表1 数值计算结果的比较 Table 1 Comparisons of numerical results |
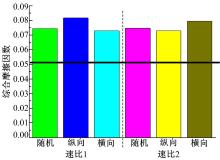
在混合弹流润滑中, 综合摩擦力是油膜剪切力与粗糙面峰点干摩擦力之和。不同类型的粗糙面有不同的压力和膜厚分布, 所以油膜剪切力与粗糙面承载率也各不相同。综合摩擦因数是综合摩擦力与外载荷的比值, 与速度、粗糙面承载率和粗糙面类型等密切相关。图9是主动轮转速为375 r/min, 啮合线上节点的综合摩擦因数, 水平方向的黑线是稳态弹流润滑计算得到的光滑齿面摩擦因数(0.052)。
由图9可知, 对于普通的无轴向速度的直齿轮应优先选择应力和摩擦因数都比较小的横向粗糙面; 而对于有轴向速度的直齿轮, 就要衡量轴向速度引起的压力和摩擦因数变化效应, 因此可以考虑纵向粗糙面。
建立了有限长线接触混合弹性流体动压润滑数学模型, 采用多重网格算法对控制方程组进行数值求解, 研究了3种典型的粗糙面在不同速比下的油膜压力分布、膜厚分布、粗糙面承载率和综合摩擦因数。结果显示:油膜速度与粗糙面纹理平行或垂直时, 分别会出现“ 排水” 或“ 泵” 现象, 从而改变油膜厚度和粗糙面承载率, 进而引起综合摩擦因数的变化; 轴向速度在油膜压力、综合摩擦因数方面对横向粗糙面的影响要大于纵向粗糙面。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|