基于支持向量机的多载量小车实时调度

引用本文

周炳海, 徐佳惠. 基于支持向量机的多载量小车实时调度. 吉林大学学报:工学版, 2016, 46(6): 2027-2033
ZHOU Bing-hai, XU Jia-hui. SVM-based real-time scheduling approach of multi-load carries. Journal of Jilin University Engineering and Technology Edition, 2016, 46(6): 2027-2033 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201606036
Permissions

基于支持向量机的多载量小车实时调度

周炳海, 徐佳惠

同济大学机械与能源工程学院,上海 201804

作者简介:周炳海(1965-),男,教授,博士生导师.研究方向:离散系统建模、调度与仿真.

基金项目:国家自然科学基金项目(71471135,61273035)

摘要

为了有效地解决车辆装配系统中多载量小车的实时调度问题,提出了基于支持向量机的实时调度方法。首先对多载量小车的实时调度问题进行描述,同时建立以车辆装配线产量和物料搬运距离作为评价指标的目标函数。然后通过车辆装配线的物料搬运系统仿真生成样本离线训练支持向量机模型,在实时阶段利用支持向量机模型实现多载量小车“等待”或“搬运”的调度决策。试验结果表明,本文提出的方法明显优于最小批量法,其运行速度快、实时调度效果好,且对动态环境变化具有一定的自适应性,能够有效提升多载量小车的实时调度水平。

关键词: 人工智能; 多载量小车; 支持向量机; 实时调度; 物料搬运

中图分类号:TP29 文献标志码:A 文章编号:1671-5497(2016)06-2027-07

SVM-based real-time scheduling approach of multi-load carries

ZHOU Bing-hai, XU Jia-hui

School of Mechanical Engineering, Tongji University, Shanghai 201804, China

Abstract

To tackle the real-time scheduling problem of multi-load carriers in automobile assembly lines, a real-time scheduling approach was proposed based on Support Vector Machine (SVM). First, the real-time scheduling problem of multi-load carriers is formally described, and an objective function of assembly line output and the delivery distance is set up. Then, samples are generated by the simulation of the assembly line with material handling system to train an SVM model offline. Finally, the trained SVM model is used in the real-time scheduling process to make “wait” or “deliver” decisions. Experimental results indicate that the proposed approach outperforms the Minimum Batch Size (MBS) approach. It runs fast, performs well and to some degree adapts to the changes in the dynamic environment. It can be effectively used to improve the real-time scheduling of multi-load carries.

Key words: artificial intelligence; multiple-load carriers; support vector machine(SVM); real-time scheduling; material handling

Show Figures

0 引言

如今的汽车制造业多采用搬运能力较高的多载量小车(Multiple-load carrier)^[1]进行物料搬运。由于车辆装配系统的复杂性, 如何提升多载量小车的实时调度水平已成为实现汽车制造业提高效率、降低成本的重要手段。

物料搬运系统的调度问题通常具有动态性、随机性和多目标性等特征, 而目前关于动态调度方法的研究成果主要集中于一般制造系统中基于单一或复杂规则的调度方法^[1]。如文献[2, 3]分别采用了最短搬运时间先服务(STTF)规则和最长输出队列(MOQS)规则进行实时调度。Wu等^[4]基于匈牙利算法来解决调度问题。一些学者通过仿真、改进型启发式算法、机器学习等方法对物料搬运系统的调度进行优化。如Hsieh等^[5]将物料搬运系统(MHS)分为若干非重叠的子系统, 每个子系统都包含一定数量的自动导向车(Automated guided vehicle, AGV)小车, 并运用仿真确定AGV小车的最优数量及资源分配。Godinho等^[6]围绕调度问题、评价指标、解决方法等6个方面, 对运用遗传算法解决FMS调度问题进行了研究。

随着对单载量搬运设备的研究日趋完善, 对于多载量小车的研究也受到越来越多的重视^[7]。如朱琳等^[8]以物料搬运时间最短为目标, 提出了一种改进的遗传算法, 对FMS中AGV小车任务进行分配和排序。Chen等^[9]基于神经网络和知识库, 考虑到产品配比对多载量小车实时调度的影响, 比较了不同的搬运任务选择和排序规则。Fathi等^[10]以搬运次数和线边库存的最小化为目标, 改进模拟退火算法来确定多载量小车搬运的零件种类和数量。上述文献主要研究了多载量小车的资源分配和任务排序问题^[11], 而目前对于是否搬运、何时开始搬运的调度决策问题鲜有涉及。

本文引入支持向量机(Support vector machine, SVM), 结合仿真技术, 针对装配线中物料搬运的调度决策问题, 提出了基于SVM的多载量小车实时调度方法, 并以产量和物料搬运距离作为评价指标建立目标函数, 评价调度性能。

1 问题描述

车辆装配线物料搬运系统将装配线分为若干个装配区域(见图1), 每个装配区域由若干辆多载量小车负责其所有工作站(Work station)的物料配送。

	Figure Option View Download New Window
	图1 车辆装配线的一个装配区域Fig.1 A united layout of MHS in assembly line

为有效说明此类调度问题, 做如下基本假设:①采用再订购点法(Reorder point policy, ROP)生成物料搬运任务; ②搬运过程不可中断, 即一旦进行物料搬运, 必须完成所有任务; ③不考虑多载量小车的失效情况; ④多载量小车的行驶速度V恒定, 无堵塞情况; ⑤多载量小车每次最多配送N_c个料箱; ⑥对于每种零件, 多载量小车每次最多使用一个料箱; ⑦一个料箱一次只能装载一种零件, 且装载数量一定, 记为SPQ_i(Standard pack quantity); ⑧多载量小车装载一个料箱的时间为LT, 卸载时若剩余零件数量小于等于SPQ_i的10%, 卸料时间为UT, 否则为UT', UT'> UT, 且LT、UT和UT'为定值; ⑨若同一时间的搬运任务数大于N_c, 则采用SSFP(Smallest slack-time first picked)规则选取搬运任务, 并根据SDFD(Shortest distance first delivered)规则完成相应的物料配送; ⑩一个装配区域仅有一辆多载量小车。

为了深入分析问题, 对物料搬运系统中的相关变量描述如下:装配区域设有工作站S_j(j=1, 2, …, s), 可进行M₁, M₂, …, M_N(N∈ N⁺)种型号的车辆装配, 其产品配比m=(ρ ₁, ρ ₂, …, ρ _N), ρ ₁+ρ ₂+…+ρ _N=1。装配共需p种零件, 即P_i(i=1, 2, …, p); 线边的实时库存量为BF_i; 平均消耗速度为U_i; 再订购点为R_i, R_i=[(D_i+2D_max)/V+N_c(LT+UT)]× U_i; D_i、D_max分别为搬运零件P_i的行驶距离及最远行驶距离。且考虑到装配线边零件缓存区的空间有限, 若R_i> 0.5× SPQ_i, 则取R_i=0.5× SPQ_i。当BF_i≤ R_i时, 向调度系统发出补货需求。

令T为总的调度时长, 调度系统的决策点t_k(k=1, 2, …)∈ T。决策点是指在调度的实时阶段, 调度系统受到某些事件的影响, 如多载量小车由“ 忙” 变为“ 空闲” 、新增搬运任务等, 触发调度系统选择让多载量小车“ 等待” 或“ 搬运” 的时刻。系统在每个决策点t_k的实时状态定义为:

$\begin{matrix} X_{k} = (B F_{1}, B F_{2}, \dots, B F_{p}, {t^{L}}_{1}, {t^{L}}_{2}, \dots, {t^{L}}_{p}) \end{matrix}$ (1)

式中: $\begin{matrix} {t^{L}}_{i} \end{matrix}$ 为若此刻不配送零件P_i, 其剩余库存可维持的装配时间, 即P_i将发生缺货的时间, $\begin{matrix} {t^{L}}_{i} \end{matrix}$ 的计算需要利用前瞻信息, 即装配线在未来对该类零件的需求信息。BF_i和 $\begin{matrix} {t^{L}}_{i} \end{matrix}$ 分别代表了系统当前和未来对零件P_i的需求程度。

调度系统在决策点t_k的调度决策记为Y_k, 若“ 0” 代表“ 等待” , “ 1” 代表“ 搬运” , 则本文的多载量小车的实时调度问题可转化为一个“ 0-1” 两类数据的分类问题, 即:

$\begin{matrix} Y_{k} = W (X_{k}) = \{\begin{matrix} 0, 等待 \\ 1, 搬运 \end{matrix} \end{matrix}$ (2)

由于装配系统的动态性, 两个决策点之间的时间可能很短, 因此BF_i必须根据调度决策Y_k实时更新, 可得:BF_i( $\begin{matrix} t_{k}^{+} \end{matrix}$ )=BF_i( $\begin{matrix} t_{k}^{-} \end{matrix}$ )+Y_k× SPQ_i。其中BF_i( $\begin{matrix} t_{k}^{-} \end{matrix}$ )、BF_i( $\begin{matrix} t_{k}^{+} \end{matrix}$ )分别为决策点t_k实行Y_k前、后的实时库存量。当系统运行至下一个决策点t_k+₁时, 则BF_i(t_k+₁)=BF_i( $\begin{matrix} t_{k}^{+} \end{matrix}$ ), 结合t_k+₁时刻的实时信息进行决策Y_k+₁, 实现多载量小车的实时调度。

选择车辆装配线产量和物料搬运距离作为评价指标建立目标函数, 并采用权重和的标量化方法将其转化为单目标函数, 即:

$\begin{matrix} f (T) = Q ω_{Q} + D ω_{D} \end{matrix}$ (3)

式中:Q为产量; D为搬运距离; ω _Q、ω _D分别为对应的权重因子, ω _Q为单位产量价值, ω _D为单位物料搬运成本, 一般ω _Q取正值, ω _D取负值, 且 $\begin{matrix} |ω_{Q}| \end{matrix}$ 远大于 $\begin{matrix} |ω_{D}| \end{matrix}$ , 即物料搬运系统应尽量满足制造系统对物料的需求。

显然, f(T)值越大, 表示物料搬运的调度性能越好。因此, 对于多载量小车的实时调度方法, 应该能够实现如式(3)所定义的目标函数的最大化。

2 实时调度方法

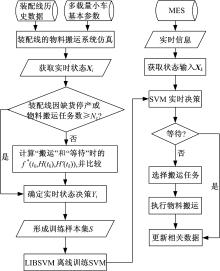
针对调度问题的动态性, 根据多载量小车的实时调度问题与数据分类之间的相似性, 提出了基于支持向量机的多载量小车实时调度方法, 其基本框架如图2所示, 主要包括离线SVM模型训练和基于SVM实时决策两个阶段。

	Figure Option View Download New Window
	图2 SVM实时调度方法基本框架Fig.2 Framework of SVM-based scheduling approach

2.1 离线SVM训练

在离线阶段, 调度系统通过仿真随机生成一组系统状态X_k(k=1, 2, …), 并确定这些状态对应的最优调度决策Y_k。利用这组状态及其对应的最优调度决策作为训练样本进行SVM的训练。

2.1.1 生成训练样本

通过离散事件仿真不难获取系统的实时状态X_k, 但问题的关键在于如何确定某个实时状态下的最优决策Y_k。

为了确定调度系统在决策点t_k执行某个决策时对应的价值, 定义系统在t_k时所能获得的最高目标函数值为:

$\begin{matrix} f^{*} (t_{k}, H (t_{k}), H^{'} (t_{k})) \end{matrix}$ (4)

式中:H(t_k)为t_k时刻已经生成的搬运任务; H'(t_k)为预计在区间(t_k, t_k+L]内将生成的搬运任务, L为前瞻时间。

在t_k时刻, 调度系统可以选择“ 等待” 或“ 搬运” , 因此在决策点t_k处的最高目标函数值为分别选择“ 等待” 或“ 搬运” 之后所能获得的最高目标函数值的较大者, 即:

f^*(t_k, H(t_k), H'(t_k))=max{g^*(t_k, H(t_k),

H'(t_k)), f^*(t_k+₁, H(t_k+₁), H'(t_k+₁))} (5)

式中:g^*(t_k, H(t_k), H'(t_k))为调度系统在t_k时刻选择“ 搬运” 的最大目标函数值, 即:

$\begin{matrix} g^{*} (t_{k}, H (t_{k}), H^{'} (t_{k})) = f_{m} (H (t_{k})) + f^{*} (t'_{k}, H (t'_{k}), H^{'} (t'_{k})) \end{matrix}$ (6)

式中:t'_k为在t_k选择搬运并完成搬运任务后变成空闲状态的时刻; f_m(H(t_k))为在该次搬运过程中的系统目标函数值, 且:

$\begin{matrix} f_{m} (H (t_{k})) = ω_{Q} \cdot \frac{t_{w}}{CT} + ω_{D} \cdot d_{H} (H (t_{k})) \end{matrix}$ (7)

式中:t_w为期间装配线的实际装配时间; CT为装配周期; t_w/CT为该段时间内的装配线产量; d_H(H(t_k))为本次搬运过程中的行驶距离。

根据式(5)(6)可得:

$\begin{matrix} \begin{matrix} f^{*} (t_{k}, H (t_{k}), H' (t_{k})) = \max {f^{*} (t_{k + 1}, H (t_{k + 1}), \\ H' (t_{k + 1})), f_{m} (H (t_{k})) + f^{*} (t'_{k}, H (t'_{k}), H' (t'_{k}))} \end{matrix} \end{matrix}$ (8)

由式(8)可知, 调度系统在决策点t_k时, 通过递归方法得到在时间段(t_k, t_k+L]内的最高目标函数值f^*(t_k, H(t_k), H'(t_k))及其对应的最优决策Y_k。值得注意的是, 如果在决策点t_k时某零件缺货导致装配线暂停或已经生成的搬运任务数大于等于N_c, 则Y_k只能为“ 1” , 即必须立即让多载量小车执行已有的搬运任务。因此, 通过仿真生成实时状态X_k, 结合以上递归运算得出最优决策Y_k, 得到一个SVM训练样本(X_k, Y_k)。l个样本形成训练样本集S=(X, Y)={(X_k, Y_k)|k=1, 2, …, l}, 其中, X∈ Rⁿ, Y={0, 1}, n为系统实时状态的特征量个数(即SVM有n个输入量, 本文中n=2p)。但是, 在实际操作过程中, 很难获取关于装配线物料搬运过程完整的实时数据, 因此, 采用eM-Plant仿真软件来模拟真实的调度过程, 收集相关样本数据。

2.1.2 训练SVM

SVM是一种新型机器学习方法, 具有理论严密、适应性强、全局优化、训练效率高和泛化性能好等优点, 并在一定程度上克服了维数灾难和过学习等传统困难。在多载量小车的实时调度过程中, 调度系统只需判断在决策点时的最佳决策是“ 等待” 或“ 搬运” , 故采用SVM模型对多载量小车的实时状态进行“ 等待” 或“ 搬运” 决策。

SVM模型的原始优化问题为:

$\begin{matrix} \{\begin{matrix} \min \frac{1}{2} ω^{T} ω + C \overset{l}{\sum_{i = 1}} ξ_{i} \\ s.t. Y_{i} (ω^{T} Φ (X_{i}) + b) \geq 1 - ξ_{i} \\ ξ_{i} \geq 0, \forall i = 1, 2, \dots, l \end{matrix} \end{matrix}$ (9)

式中:ω 为多维分类面的法向量; b为多维分类面与坐标原点之间的距离; ξ _i为松弛变量。

其对偶形式为:

$\begin{matrix} \{\begin{matrix} \min \frac{1}{2} \overset{l}{\sum_{i = 1}} \overset{l}{\sum_{j = 1}} Y_{i} Y_{j} K (X_{i}, X_{j}) α_{i} α_{j} - \overset{l}{\sum_{i = 1}} α_{i} \\ s.t. 0 \leq α_{i} \leq C, \forall i = 1, 2, \dots, l \end{matrix} (10) \end{matrix}$

式中:K(X_i, X_j)=Φ $\begin{matrix} (X_{i})^{T} \end{matrix}$ Φ (X_j)为核函数, 本文选用径向基核函数(Radical basic function, RBF), 即K(X_i, X_j)=exp(-γ $\begin{matrix} ‖ X_{i} - X_{j} ‖^{2} \end{matrix}$ ); γ 为核参数, 控制了核函数的径向作用范围, 反映了训练样本集的特征; C为惩罚系数, 用于控制被最优分割平面错分的样本数, 其平衡模型的计算复杂度和错误分类程度。

C和γ 是训练SVM时的两个关键参数, 对于SVM及参数说明详见文献[12]。在求解式(10)后构造决策函数进行数据分类, 即:

$\begin{matrix} \begin{matrix} f (X) = sgn (ω^{T} Φ (X) + b) = \\ sgn (\overset{l}{\underset{i = 1}{\sum Y_{i} α_{i} K}} (X_{i}, X) + b) \end{matrix} \end{matrix}$ (11)

综上所述, SVM训练可分为以下3个步骤:

(1)确定输入特征量个数n、收集训练样本集S、选择SVM模型;

(2)通过RBF将S中的数据映射到高维特征空间(Hilbert空间)中、选取C和γ 、求解式(10)获得(ω , b)及对应的支持向量α ;

(3)通过(ω , b)及支持向量α 建立多载量小车的实时调度决策模型。

本文采用LIBSVM^[13]训练SVM, 并应用到实时SVM决策中。

2.2 实时SVM调度决策

在实时阶段, 调度系统不断从装配线的制造执行系统(Manufacturing execution system, MES)获取实时信息, 当到达决策点t_k时, 构造一个用于SVM分类的实时状态作为SVM的输入, 即X_k=(BF₁, BF₂, …, BF_p, $\begin{matrix} {t^{L}}_{1} \end{matrix}$ , $\begin{matrix} {t^{L}}_{2} \end{matrix}$ , …, $\begin{matrix} {t^{L}}_{p} \end{matrix}$ )。然后利用训练好的SVM确定该输入的分类Y_k为0或1。若为“ 0” , 则多载量小车继续等待, 直至下一个决策点t_k+₁; 否则, 调度系统分别根据SSFP和SDFD规则选择搬运任务并确定搬运次序, 执行搬运任务, 结束搬运后等待下一个决策点t_k+₁。如此循环往复, 实现多载量小车的实时调度。

3 仿真试验及分析

3.1 仿真案例参数

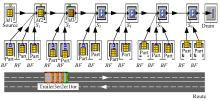
本案例来源于美国通用汽车公司某个汽车装配区域的实际数据。该汽车装配线共生产3种车型M₁、M₂和M₃, 且m=(0.2, 0.5, 0.3)。仿真设6个装配工作站S₁~S₆, 14种零件P₁~P₁₄, 表1列出了物料清单、SPQ_i和零件库存区到各卸料点之间距离D_i。该装配线周期时间CT为72 s, 各工作站的工作时间服从最小值为70 s、最大值为75 s、众数为72 s的三角分布, 且平均故障间隔时间为54 min, 平均恢复时间为12 s。多载量小车的速度V=3.05 m/s, N_c=3, LT=36.6 s, UT=43.2 s, UT'=103.2 s。使用eM-Plant软件建立仿真模型, 其布局如图3所示。

表1 物料清单、SPQ_i及搬运距离 Table 1 BOM, SPQ_i and delivery distance

	Figure Option View Download New Window
	图3 车辆装配线仿真布局Fig.3 Layout of an assembly line simulation

3.2 SVM训练及验证

通过仿真生成训练样本S=(X, Y)={(X_k, Y_k)|k=1, 2, …, 6000}, LIBSVM默认惩罚系数C=1, 核参数γ =1/n, 选用RBF, 运用LIBSVM训练SVM。为了验证SVM分类模型的性能, 进行K-CV交叉验证(K-fold cross validation), 可有效地避免过学习和欠学习状态的发生, 经K-CV可得分类准确率达88.7159%。对于该6000个样本数据, 取其中的4000个作为训练集训练模型, 2000个作为验证集进行验证, 此时分类准确性达93.5665%。运用训练好的SVM进行多载量小车的实时调度, 单次调度决策所需时间约为0.016545 s。因此, 无论是准确度还是响应速度, 本文方法都适用于实际的生产调度。

3.3 调度性能比较

为了有效地评价本文方法性能, 以目标函数值作为评价指标, 通过试验与最小批量法(Minimum batch size, MBS)^[14]性能进行比较。x为最小批量, 根据MBS-x规则, 如果当前需要处理的搬运任务数少于x, 那么多载量小车继续等待; 否则开始搬运。

分别取x=1, 2, 3, 即共有4种调度方法, 每种方法进行20次仿真, 每次仿真时间为240 h, 其中包括24 h的预热时间。

3.3.1 默认参数设置下的性能比较

取ω _Q=1, ω _D=-0.002 62, 按照3.1节中参数进行仿真。表2为分别使用SVM、MBS-1、MBS-2和MBS-3方法的仿真结果。由表2可知, 随着最小批量x的增大, MBS-x方法得到的产量和搬运距离均逐渐减少, 目标函数值变大。SVM方法与最佳的MBS-3方法在物料搬运距离上相差较少, 但产量却提高了3.79%, 因此目标函数最大。与MBS-1、MBS-2、MBS-3方法相比, SVM方法的性能分别提高了14.30%、4.58%以及3.34%。

表2 不同调度方法的性能比较 Table 2 Performance of different approaches

3.3.2 不同R_i设置下的性能比较

由于所有的调度方法都根据再订购点法生成补货需求, 考虑到不同的R_i设置可能对调度方法的性能产生影响, 因此通过设定不同的再订购点进行仿真, 从而更充分地评价SVM方法性能。如表3所示, 本次仿真试验共设定10组不同的再订购点R_i。

试验结果如图4所示, 从图4可以看出:这4种调度方法的目标函数值都随着R_i的变化发生较大变化。如SVM方法在第1组R_i设置下目标函数值为8509.56, 在第6组时为9895.08, 两者相差16.3%。随着R_i增大, 目标函数值均显著增大, 当达到第6组(即默认的R_i设置)及以后, 目标函数值波动较小, 且SVM方法的目标函数值均远大于MBS-1、MBS-2和MBS-3方法。因此, 即使采用不同的R_i设置, 本文所提出的基于SVM的实时调度方法优于MBS-x调度方法。

表3 不同的R_i设置 Table 3 Different setting of R_i

	Figure Option View Download New Window
	图4 不同R_i设置下的目标函数值比较Fig.4 Comparison of performances with different R_i

3.3.3 动态环境中的调度性能比较

为了验证本文方法能够适应动态环境的调度需求, 本节将比较这些方法在不同的产品配比m和调度目标权重ω _Q、ω _D设定下的性能。

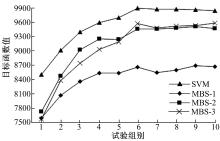
(1)改变产品配比m

如表4所示, 共设定8组不同的m, 试验结果如图5所示。随着m的变化, 各调度方法的目标函数值均发生变化, SVM方法的目标函数值整体高于MBS-x方法。因此, 与MBS-x方法相比, SVM方法对产品配比(即对实际的市场需求)变化的适应性较好。

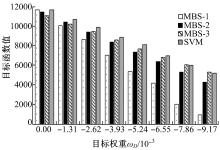
(2)改变调度目标权重ω _Q、ω _D

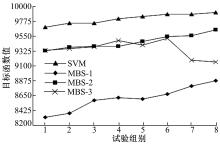
为便于比较, 设定ω _Q=1保持不变, ω _D从0到-0.009 17取8个不同的值进行试验, 试验结

表4 不同的m设置 Table 4 Different setting of m

	Figure Option View Download New Window
	图5 不同m设置下的目标函数值比较Fig.5 Comparison of performances with different m

果如图6所示。由图6可知, 各个调度方法的目标函数值都随着ω _D的变化而变化。当 $\begin{matrix} |ω_{D}| \end{matrix}$ 较大(ω _D较小)时, 即每单位搬运距离对应的搬运成本增加, 目标函数值都较低, 相反则较高。在这8组不同的调度目标权重设置中, SVM方法的目标函数值整体优于其他方法。但是, 当ω _D较小时, 即单位物料搬运成本对调度目标影响较大时, SVM方法的目标函数值略低于MBS-3方法; 当ω _D=0, 即只考虑产量时, SVM的目标函数值略低于MBS-1方法。因此, 当某一调度目标的权重远大于其他调度目标权重时, SVM方法仍有待进一步优化以提高物料搬运调度的性能。

	Figure Option View Download New Window
	图6 不同ω _Q, ω _D下的目标函数值比较Fig.6 Comparison of performances with different ω _Q and ω _D

综上所述, SVM方法能够根据动态制造环境中的产品配比、调度目标权重等因素的变化, 通过SVM的机器学习做出相同状态下的最佳决策, 具有一定的自适应性。

4 结束语

针对车辆装配系统中物料搬运系统的特点, 提出了基于支持向量机的多载量小车实时调度方法。在离线阶段建立装配线物料搬运系统的仿真模型, 生成样本训练SVM模型; 在实时调度阶段利用SVM确定多载量小车等待或搬运的决策。试验结果表明:本文提出的实时调度方法准确率高, 调度效果好; 在实时阶段运行快速, 符合实时调度需求, 且对动态环境变化具有一定的自适应性。但是, 本文仅对单个多载量小车的实时调度方法进行了探讨, 今后将针对一个物流区域同时使用多个搬运设备及多个物流区域间相互关联的情况对多载量小车的实时调度进行深入探究。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Chang Q, Pan C, Xiao G, et al. Integrated modeling of automotive assembly line with material hand ling[J]. Journal of Manufacturing Science and Engineering, 2013, 135(1): 011018. [本文引用:2]
[2]	Egbelu P J, Tanchoco J M A. Characterization of automatic guided vehicle dispatching rules[J]. International Journal of Production Research, 1984, 22(3): 359-374. [本文引用:1]
[3]	Sabuncuoglu I. A study of scheduling rules of flexible manufacturing systems: a simulation approach[J]. International Journal of Production Research, 1998, 36(2): 527-546. [本文引用:1]
[4]	Wu L H, Mok P Y, Zhang J. An adaptive multi-parameter based dispatching strategy for single-loop interbay material hand ling systems[J]. Computers in Industry, 2011, 62(2): 175-186. [本文引用:1]
[5]	Hsieh C H, Cho C, Yang T, et al. Simulation study for a proposed segmented automated material hand -ling system design for 300-mm semiconductor fabs[J]. Simulation Modelling Practice and Theory, 2012, 29(1): 18-31. [本文引用:1]
[6]	Godinho F M, Barco C F, Neto R F T. Using genetic algorithms to solve scheduling problems on flexible manufacturing systems (FMS): a literature survey, classification and analysis[J]. Flexible Services and Manufacturing Journal, 2014, 26(3): 408-431. [本文引用:1]
[7]	Ho Y, Liu H, Yih Y. A multiple-attribute method for concurrently solving the pickup-dispatching problem and the load-selection problem of multiple-load AGVs[J]. Journal of Manufacturing Systems, 2012, 31(3): 288-300. [本文引用:1]
[8]	朱琳, 范秀敏, 何其昌. 柔性生产系统配料区多自动导航小车调度优化[J]. 计算机集成制造系统, 2012, 18(6): 1168-1175. Zhu Lin, Fan Xiu-min, He Qi-chang. Scheduling optimization for multi-AGVs in batching area of flexible production system[J]. Computer Integrated Manufacturing Systems, 2013, 18(6): 1168-1175. [本文引用:1]
[9]	Chen C, Xi L F, Zhou B H, et al. A multiple-criteria real-time scheduling approach for multiple-load carriers subject to LIFO loading constraints[J]. International Journal of Production Research, 2011, 49(16): 4787-4806. [本文引用:1]
[10]	Fathi M, Alvarez M J, Hassani M F, et al. A multiobjective optimization algorithm to solve the part feeding problem in mixed-model assembly lines[J]. Mathematical Problems in Engineering, 2014, 2014: 654053. [本文引用:1]
[11]	赵芳, 马玉磊. 自训练半监督加权球结构支持向量机多分类方法[J]. 重庆邮电大学学报: 自然科学版, 2014, 26(3): 404-408. Zhao Fang, Ma Yu-lei. Multi-class classification based on self-training semi-supervised weighted sphere structured support vector machine[J]. Journal of Chongqing University of Posts and Telecommunications(Natural Science Edition), 2014, 26(3): 404-408. [本文引用:1]
[12]	邓乃扬, 田英杰. 支持向量机——理论、算法与拓展[M]. 北京: 科学出版社, 2009. [本文引用:1]
[13]	Chang C C, Lin C J. LIBSVM: a library for support vector machines[DB/OL]. [2015-04-25]. https://www.csie.ntu.edu.tw/~cjlin/papers/libsvm.pdf. [本文引用:1]
[14]	Neust M F. A general class of bulk queues with Poisson input[J]. The Annals of Mathematical Statistics, 1967, 38(3): 759-770. [本文引用:1]

2013

0.0

... 0 引言如今的汽车制造业多采用搬运能力较高的多载量小车(Multiple-load carrier)^[1]进行物料搬运 ...

... 物料搬运系统的调度问题通常具有动态性、随机性和多目标性等特征,而目前关于动态调度方法的研究成果主要集中于一般制造系统中基于单一或复杂规则的调度方法^[1] ...

1984

0.0

1998

0.0

2011

0.0

... Wu等^[4]基于匈牙利算法来解决调度问题 ...

2012

0.0

... 如Hsieh等^[5]将物料搬运系统(MHS)分为若干非重叠的子系统,每个子系统都包含一定数量的自动导向车(Automated guided vehicle,AGV)小车,并运用仿真确定AGV小车的最优数量及资源分配 ...

2014

0.0

... Godinho等^[6]围绕调度问题、评价指标、解决方法等6个方面,对运用遗传算法解决FMS调度问题进行了研究 ...

2012

0.0

... 随着对单载量搬运设备的研究日趋完善,对于多载量小车的研究也受到越来越多的重视^[7] ...

2012

0.0

. 2012, 18(6):1168-1175

Scheduling optimization for multi-AGVs in batching area of flexible production system

柔性生产系统配料区多自动导航小车调度优化

Zhu Lin , Fan Xiu-min , He Qi-chang.

朱琳, 范秀敏, 何其昌

为解决配料区物料运输多自动导航小车的调度问题,以自动导航小车给柔性生产系统配料区补料搬运时间最短为目标建立数学模型,提出了一种改进的遗传算法进行自动导航小车的任务分配和任务排序优化。算法采用了整数编码和多参数编码相结合的方式,同时为避免常规交叉变异算子易出现非法解的状况,采用了对离散随机种群中染色体进行扩展的初始种群生成方法和分段式交叉变异算子, 优化结果给出了多自动导航小车的任务分配方案。通过某重型机械公司的装配车间内多自动导航小车调度的优化实例,并与分支定界算法和未改进的遗传算法进行结果对比,验证了该方法的有效性和可行性。

... 如朱琳等^[8]以物料搬运时间最短为目标,提出了一种改进的遗传算法,对FMS中AGV小车任务进行分配和排序 ...

2011

0.0

... Chen等^[9]基于神经网络和知识库,考虑到产品配比对多载量小车实时调度的影响,比较了不同的搬运任务选择和排序规则 ...

2014

0.0

... Fathi等^[10]以搬运次数和线边库存的最小化为目标,改进模拟退火算法来确定多载量小车搬运的零件种类和数量 ...

2014

0.0

. 2014, 26(3):404-408 DOI:doi:10.3979/j.issn.1673-825X.2014.03.022

Multi-class classification based on self-training semi-supervised weighted sphere structured support vector machine

自训练半监督加权球结构支持向量机多分类方法

Zhao Fang , Ma Yu-lei.

赵芳, 马玉磊

针对自训练半监督支持向量机算法中的低效问题,采用加权球结构支持向量机代替传统支持向量机,提出自训练半监督加权球结构支持向量机.传统支持向量机需要求解二次凸规划问题,在处理大规模数据时会消耗大量存储空间和计算时间,特别是在多分类问题上更加困难.利用球结构支持向量机进行多类别分类,大大缩短了训练时间,降低了算法复杂度.球结构支持向量机在不同类别样本数目不均衡时训练分类错误倾向于样本数目较小的类别,通过权值的引入,降低了球结构支持向量机对样本不均衡的敏感性,补偿了类别差异对算法推广性能造成的不利影响.在人工数据集和UCI(university of california irvine)数据集上的实验结果表明,该方法对有标记样本的鲁棒性较好,不仅能够提高效率,且分类精度也有显著提高.

... 上述文献主要研究了多载量小车的资源分配和任务排序问题^[11],而目前对于是否搬运、何时开始搬运的调度决策问题鲜有涉及 ...

2009

0.0

... 本文采用LIBSVM^[13]训练SVM,并应用到实时SVM决策中 ...

1967

0.0

... 3 调度性能比较为了有效地评价本文方法性能,以目标函数值作为评价指标,通过试验与最小批量法(Minimum batch size,MBS)^[14]性能进行比较 ...