首先, 给定一个图G, 对于每一对节点v_i和v_j之间的相似度vs(v_i, v_j)可以由Jaccard相似度^[18]计算得出:

vs(vi, vj)=Ni⋂NjNi⋃Nj (1)

式中:N_i为v_i邻居节点的集合; |N_i|为N_i中节点的个数。节点对之间的相似度值越高, 表明它们越相似。

网络中节点之间的局部距离(Jaccard距离)可表示为:

Vsd(vi, vj)=1-vs(vi, vj)=1-Ni⋂NjNi⋃Nj (2)

从式(2)可以看出, 节点越相似, 节点间距离越近。该方法不仅计算时间短而且可以较直观地描述节点之间的局部距离。

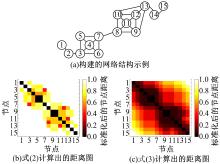
对于图1(a)所示的网络结构, 利用式(2)计算得到的距离标准化后的距离图如图1(b)所示, 可以清楚看出该方法也存在弊端:只能度量网络中最短距离小于等于2的节点之间的距离, 当两个节点间最短距离大于2时, Vsd均为1, 即Vsd只能度量节点之间的局部距离, 不能度量节点之间的全局距离。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 网络结构示例Fig.1 Demo network

为了克服式(2)不能度量节点间的全局距离这一弊端, 本文引入网络中节点间的最短距离ShortestDis, 并将其与Vsd进行整合, 提出新的距离度量VsdSD:

VsdSDvi, vj=Vsdvi, vj×ShortestDisvi, vj(3)

式中:ShortestDis(v_i, v_j)为节点v_i到节点v_j最短路径的距离。

对于图1(a)所示的网络结构, 利用式(3)计算得到的距离标准化后的距离图如图1(c)所示。可以看出, VsdSD能够很好地度量节点间的全局距离, 不同节点集合(节点1~7和节点8~15)中的节点取得相对远的距离, 同时相同节点集合(节点1~7或节点8~15)中的节点取得相对近的距离。后面的实验将证明VsdSD同样适用于其他复杂网络。

由于社区是由一些相似度较高并且距离较近的节点所组成的局部子网络, 而式(3)中定义的VsdSD不仅解决了相似度距离度量的问题而且还使得局部连接紧密的点距离更近, 所以本文试图将VsdSD用于探究复杂网络的社区结构。

社区发现本质上是一个图聚类过程, 所以本文引入一种无监督聚类算法— — 密度峰值聚类(DPC)^[17]来解决图聚类问题。该算法基于两个重要假设:①聚类中心由低局部密度的临近节点围绕; ②聚类中心与任意比其局部密度高的节点具有相对远的距离。对于任意一个节点i, 必须计算节点的局部密度ρ _i以及节点到其他具有更高局部密度的节点的距离δ _i这两个变量。并且这两个变量的值均只取决于节点对之间的距离。其中, 节点i的局部密度ρ _i为:

ρi=∑ηjdisij-disc(4)

式中:dis_c为截断距离。如果dis_ij-dis_c< 0, 则η (dis_ij-dis_c)=1; 否则, η (dis_ij-dis_c)=0。

节点i到其他具有更高局部密度节点的最小距离δ _i为:

δi=minj:ρj> ρidisij(5)

当节点i具有最大密度时, δ _i=max_j(dis_ij)。根据上述定义可知, 具有最大局部密度的节点一定是聚类中心点。在得到所有ρ _i和δ _i的值后, 算法会得到一个决策图, 图中具有高δ 值和相对较高ρ 值的节点会被选作聚类中心。在聚类中心确定之后, 剩余的节点将会按照局部密度从高至低分派到各个聚类簇中。Rodriguez等^[17]论证了DPC算法中节点分配过程的可靠性以及对大数据集的鲁棒性。

为了将DPC算法应用到社区发现中, 本文通过整合Jaccard距离和网络中节点间最短距离来度量网络中节点间的全局距离。在前面提到, DPC算法中ρ 和δ 均取决于节点对之间的距离dis_ij, 换言之, DPC算法的输入只有距离dis_ij。因此, 可以将网络中的节点集合V={v₁, v₂, …, v_n}映射为点集合DP={1, 2, …, n}, 节点v_i和v_j之间的距离VsdSD(v_i, v_j)映射为点i和j之间的距离dis_ij。

本文提出一个基于点距离和密度峰值聚类的社区发现新方法— — VDDPC, 该方法由4个主要部分组成:初始化节点邻接关系、计算节点之间的相似度、计算节点之间的距离以及应用DPC进行社区发现。VDDPC具体的步骤如下。

输入:网络G=(V, E)

Step1 初始化节点邻接关系;

Step2 计算节点之间的Jaccard相似度vs及Jaccard距离Vsd;

Step3 计算网络中节点间的最短距离ShortestDis;

Step4 将ShortestDis与Vsd相结合, 得到VsdSD;

Step5 将节点之间的VsdSD输入到密度峰值聚类算法中, 对节点进行聚类;

Step6 将聚类结果整理为社区划分结果。

输出:算法发现的社区C={C_i}

为了衡量节点之间的局部距离, VDDPC首先需要计算Jaccard距离Vsd, 时间复杂度为O(Km), 其中K≈ [ ∑i, j=1n( Ni- Ni⋂Nj)]/n, v_j∈ Ni19。使用基于堆优化的Dijkstra算法计算网络中节点间的最短路径的距离ShortestDis, 时间复杂度为O(n²logn+nmlogn)。整合Vsd和ShortestDis的时间复杂度为O(n²), DPC算法的时间复杂度为O(n²)。综上, VDDPC的总体时间复杂度为O(Km+n²logn+nmlogn+2n²)。

为了验证VDDPC的可行性和有效性, 本文选择了5个真实数据集和12个人工合成数据集进行实验。

2.1.1 真实网络数据集

表1列出5个真实数据集, 其中包括3个已知真实划分的网络数据集(空手道数据集Karate、海豚数据集Dolphin、美国大学橄榄球数据集Football)和2个没有真实划分的网络数据集(爵士乐音乐家数据集Jazz musicians、美国电网数据集Power grid)。

表1

Table 1

表1(Table 1)

表1 真实数据描述 Table 1 Real-world networks description 真实数据集 点数 边数 Karate[20] 34 78 Dolphin[21] 62 158 Football[1] 115 612 Jazz musicians[22] 198 2742 Power grid[23] 4941 6594

表1 真实数据描述 Table 1 Real-world networks description

Karate数据集由34个节点和78条边组成, 每个节点代表1个空手道俱乐部成员, 而两个节点之间的边代表着相应的成员之间联系交往紧密。由于俱乐部会长和教练之间的矛盾, 最终俱乐部分裂为两个小的俱乐部。

Dolphin数据集由62个节点和159条边组成, 每个节点代表一只生活在新西兰Doubtful Sound海峡的宽吻海豚, 而两个节点之间的边代表着两只海豚之间接触频繁。经过长时间的观察, 最终这群海豚被分为2个群体。

Football数据集由115个节点和612条边组成, 每个节点代表一只参加2000年美国大学秋季学期橄榄球赛的球队, 而两个节点之间的边代表着两只球队曾经有过一场比赛。这些球队隶属于12个不同的球会, 并且球会内部进行的比赛相对较多。

Jazz musicians数据集是由爵士乐音乐家之间的合作关系所产生的数据集, 一共有198个节点和2742条边, 其中每个节点代表着一位音乐家, 每一条边代表着两位音乐家曾合作过。

Power grid数据集是由美国电网分布产生的数据集, 一共有4941个节点和6594条边, 其中每个节点代表一个供电设备, 每一条边代表着一条供电线路。

2.1.2 人工合成网络数据集

LFR人工合成基准网络^[24]是测试社区发现算法性能的一种基准方法。LFR基准网络有两大优势:它模拟了节点度数和社区大小的无标度特征以及其已知的社区划分结构。本文中一共采用12个LFR基准网络, 具体参数如表2所示。在所有的12个网络中, 每个网络的节点N为500, 网络中节点的平均度数k为15, 节点的最大度数maxk为50, 节点的度数分布参数t₁分别为2和3, 社区大小分布参数t₂为1和2, 并且混合因子mu为0.1~0.3。这12个LFR基准网络由于其合理的变量配置, 可以充分评估算法的性能。

表2

Table 2

表2(Table 2)

表2 LFR基准网络参数列表 Table 2 Parameter list of LFR benchmark networks ID N k maxk t1 t2 mu S1 500 15 50 2 1 0.1 S2 500 15 50 2 2 0.1 S3 500 15 50 3 1 0.1 S4 500 15 50 3 2 0.1 S5 500 15 50 2 1 0.2 S6 500 15 50 2 2 0.2 S7 500 15 50 3 1 0.2 S8 500 15 50 3 2 0.2 S9 500 15 50 2 1 0.3 S10 500 15 50 2 2 0.3 S11 500 15 50 3 1 0.3 S12 500 15 50 3 2 0.3

表2 LFR基准网络参数列表 Table 2 Parameter list of LFR benchmark networks

迄今为止, 许多评价指标被用来评价社区发现算法的表现, 然而却没有统一的标准方法²⁵。本文选用归一化互信息(Normalized mutual information, NMI)^{[26, 27]}以及模块度(Q)^[2]作为社区发现算法的评价标准。

2.2.1 归一化互信息

NMI是由Lancichinetti等^[26]提出的被广泛用于测评已知网络结构划分结果的评价指标, 定义为:

NMIRP=1-HRP+HPR2 (6)

式中:R为真实的划分结果; P为预测的划分结果; H(R|P)为R关于P的归一化条件熵。NMI值的范围为0~1, NMI值越高预示算法预测的划分结果与真实的划分结果越接近。

2.2.2 模块度

模块度Q是由Girvan和Newman^[2]提出的用于评价社区结构稳定性的衡量指标, 定义为:

Q=∑Ci=1k{IM-2I+O2M)]2 (7)

式中:I为两个端点均在同一社区的边的数目; O为一个端点在社区中, 而另一个端点不在该社区中的边的数目; M为网络中的总边数。Q值越高预示划分的社区结构越稳定。

将VDDPC与4种知名算法(Infomap^[10]、LPA^[6]、Fastgreedy^[4]和Walktrap^[11])进行对比, 其算法代码均来自于igraph R代码包^[28]。

2.3.1 真实网络数据集结果分析

(1)Karate数据集

如表3所示, VDDPC将该网络划分为2个社区并取得最高的NMI值1, 即社区划分结果与真实划分完全相同。与其他算法相比, VDDPC不仅得到与真实划分完全相同的划分结果, 而且

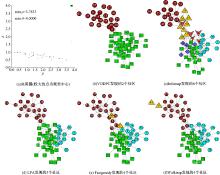
VDDPC的NMI值也明显优于Infomap的NMI值(0.5925)、LPA的NMI值(0.7029)、Fastgreedy的NMI值(0.5767)以及Walktrap的NMI值(0.3636)。将各个算法的划分结果进行对比, 如图2所示。从图2中可以清楚地看出决策图中聚类中心的选取过程以及VDDPC发现的2个社区具体划分情况。而Infomap、LPA、Fastgreedy以及Walktrap均将节点集合(5, 6, 7, 11, 17)划分到了一个小的社区, 这也使得划分结果与真实的划分结果存在很大差异。

(2)Dolphin数据集

如表3所示, VDDPC将该网络划分为2个社区并取得最高的NMI值(0.6974)。与其他算法相比, VDDPC的NMI值明显优于Infomap的NMI值(0.3102)、LPA的NMI值(0.4348)、Fastgreedy的NMI值(0.4377)以及Walktrap的NMI值(0.4100)。将各个算法的划分结果进行对比, 如图3所示。从图3可以看出:在决策图中节点14和节点46具有很高的ρ 值和δ 值, 所以选取节点14和节点46作为聚类中心, 并且VDDPC从连接非常少的部分将网络清晰划分为两个社区。Infomap将网络划分为6个社区, 社区数目比其他算法都要多, 但其NMI值却低于其他所有算法。LPA的划分结果与VDDPC的结果比较相近, 将VDDPC得到的如图3(b)中下方的社区(正方形)划分为了2个社区(正方形和五边形)。而Fastgreedy和Walktrap则分别产生了一个非常小的社区节点集合(37, 40)和节点集合(33, 61)。

表3

Table 3

表3(Table 3)

表3 已知划分的真实网络分析 Table 3 Analyze of real-world empirical networks 数据集 真实划分的 社区数目 VDDPC Infomap LPA Fastgreedy Walktrap NC NMI NC NMI NC NMI NC NMI NC NMI Karate 2 2 1 3 0.5925 3 0.7029 3 0.5767 5 0.3636 Dolphin 2 2 0.6974 6 0.3102 3 0.4348 4 0.4377 4 0.4100 Football 12 12 0.8865 12 0.9232 11 0.8865 6 0.5962 10 0.8570 注:NC为各个算法发现的社区数目; 黑体的数值为最高的NMI值。

表3 已知划分的真实网络分析 Table 3 Analyze of real-world empirical networks

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 空手道俱乐部网络的社区发现结果Fig.2 Community detection results of karate club network

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 海豚社会网络的社区发现结果Fig.3 Community detection results of dolphin social network

(3)Football数据集

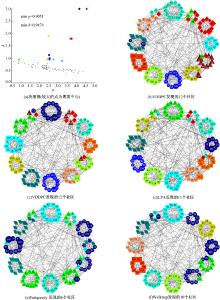
如表3所示, VDDPC将网络划分为12个社区, 并取得NMI值(0.8865), 仅低于Infomap的NMI值(0.9232), 与LPA的NMI值(0.8865)相同, 优于Fastgreedy的NMI值(0.5962)以及Walktrap的NMI值(0.8570)。可以看到, VDDPC和Infomap所发现的社区数目均与真实的社区数目相同, 并且两者的NMI结果也稍优于其他算法。将各个算法的划分结果进行对比, 如图4所示。在图4(b)~图4(f)中, 12个圆圈代表Football数据集的真实的社区划分情况, 而具有相同形状和颜色灰度的节点代表这些点被算法划分到同一个社区中。在图4(a)中, 一共有12个聚类中心被选择, 其中节点59(ρ 值约为0.91)因其具有很高的ρ 值(只低于其他11个聚类中心)和相对较高的ρ 值被选为聚类中心。从图4(b)(c)(d)(f)可以看到:VDDPC、Infomap、LPA、Walktrap几乎都将网络中的大社区划分出来并只错误划分了一部分小社区中的点, 这也使得到的社区划分结果差异并不大。图4(e)中, Fastgreedy将网络划分为6个社区, 其划分结果与真实的社区划分结果差异很大, 这也导致其NMI值远低于其他算法。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 美国大学橄榄球联盟网络的社区发现结果Fig.4 Community detection results of American college football network

表4

Table 4

表4(Table 4)

表4 未知划分的真实网络分析 Table 4 Analyze of real-world unempirical networks 数据集 VDDPC Infomap LPA Fastgreedy Walktrap NC Q NC Q NC Q NC Q NC Q Jazz musicians 3 0.4284 7 0.2800 4 0.4290 4 0.4389 11 0.4384 Power grid 56 0.8566 493 0.8150 497 0.8035 40 0.9350 364 0.8310 注:黑体的数值为最高的Q值。

表4 未知划分的真实网络分析 Table 4 Analyze of real-world unempirical networks

(4)Jazz musicians和Power grid数据集

如表4所示, 对于Jazz musicians数据集和Power grid数据集, VDDPC分别划分出3个社区和56个社区并且Q值分别为0.4284和0.8566。Infomap分别划分出7个社区和493个社区并且Q值分别为0.2800和0.8150, LPA分别划分出4个社区和497个社区并且Q值分别为0.4290和0.8035, Fastgreedy分别划分出4个社区和40个社区并且分别取得最高的Q值0.4389和0.9350, Walktrap分别划分出11个社区和363个社区并且Q值分别为0.4384和0.8310。可以看出VDDPC的Q值非常接近Fastgreedy和Walktrap取得的Q值。之所以Fastgreedy在两个数据集上均取得了最高的Q值, 是因为Fastgreedy是一种基于模块度优化的方法, 即用Q值作为其评价标准并寻求最大模块度的社区划分。而VDDPC与其他3种算法相比也表现出了足够的竞争力。Jazz musicians数据集和Power grid数据集生成的决策图如图5所示。

2.3.2 人工合成网络数据集结果分析

表5中列出了VDDPC、Infomap、LPA、Fastgreedy以及Walktrap在12个LFR基准网络上的实验结果。可以看出, 对于12个LFR基准网络, VDDPC、Infomap以及Walktrap均具有相当好的表现并均取得了最高的NMI值1, 即3种算法的社区划分结果与网络的真实划分完全相同。对于数据集S9和S10, LPA错误划分了一些节点, 这也使得其未能取得NMI值1。而随着混合因子数值的增加, Fastgreedy划分的社区结果在计算NMI时表现欠佳并且NMI值有明显的下降。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 未知划分的真实网络的决策图(较大的点为聚类中心)Fig.5 Decision graphs of unempirical networks(bigger points are clustering centers)

表5

Table 5

表5(Table 5)

表5 LFR基准网络分析 Table 5 Analysis of LFR benchmark networks 数据集 VDDPC Infomap LPA Fastgreedy Walktrap ID NF NC NMI NC NMI NC NMI NC NMI NC NMI S1 22 22 1 22 1 22 1 17 0.9092 22 1 S2 29 29 1 29 1 29 1 25 0.9459 29 1 S3 20 20 1 20 1 20 1 19 0.9729 20 1 S4 25 25 1 25 1 25 1 24 0.9731 25 1 S5 22 22 1 22 1 22 1 16 0.8357 22 1 S6 34 34 1 34 1 34 1 21 0.8287 34 1 S7 24 24 1 24 1 24 1 16 0.8333 24 1 S8 22 22 1 22 1 22 1 17 0.8810 22 1 S9 24 24 1 24 1 25 0.9945 12 0.6872 24 1 S10 33 33 1 33 1 32 0.9836 13 0.7110 33 1 S11 21 21 1 21 1 21 1 9 0.6745 21 1 S12 29 29 1 29 1 29 1 16 0.7622 29 1 注:NF为真实划分的社区数目; 黑体的数值为最高的NMI值。

表5 LFR基准网络分析 Table 5 Analysis of LFR benchmark networks

根据表2中的参数, 给出所有12个LFR基准网络的决策图(见图6)。从图6可以看出, 每个LFR基准网络的聚类中心都有着很高的ρ 值和δ 值。

从上述对比及分析可以看出, VDDPC在Karate数据集、Dolphin数据集上均取得最高的NMI值, 在Football数据集取得仅次于Infomap的NMI值, 并且VDDPC划分的社区数目均与真实的社区划分数目相同。VDDPC也分别在Jazz musicians数据集和Power grid数据集取得了较高的Q值, 这意味着VDDPC同样擅长发现稳定的社区结构。而在LFR基准网络上, VDDPC取得了最高的NMI值, 同样表现出良好的性能。实验结果充分验证了VDDPC的可行性及有效性。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 十二个LFR基准网络的决策图(较大的点为聚类中心)Fig.6 Decision graphs of 12 LFR benchmark networks (bigger points are clustering centers)