基于图像梯度预测的可调节大容量可逆数据隐藏

引用本文

韩佳伶, 赵晓晖. 基于图像梯度预测的可调节大容量可逆数据隐藏. 吉林大学学报:工学版, 2016, 46(6): 2074-2079
HAN Jia-ling, ZHAO Xiao-hui. Adjustable reversible data hiding algorithm with large embedded capacity based on image gradient prediction. Journal of Jilin University Engineering and Technology Edition, 2016, 46(6): 2074-2079 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201606042
Permissions

基于图像梯度预测的可调节大容量可逆数据隐藏

韩佳伶^1,², 赵晓晖¹

1.吉林大学通信工程学院,长春 130012

2.吉林财经大学管理科学与信息工程学院,长春 130117

作者简介:韩佳伶(1982-),女,讲师,博士.研究方向:多媒体信息安全.E-mail:weiya2000@163.com

基金项目:吉林省科技厅项目(20130101072JC); 吉林省教育厅项目(2015411)

摘要

利用图像梯度选择和判断每个像素的梯度趋势,并根据梯度和相邻像素进行预测,采用了基于预测误差的可逆隐藏方法,有效降低了预测误差,增加了算法的隐藏容量。在隐藏过程中,通过调整嵌入规则降低对宿主图像引起的失真,提高了算法的隐蔽性。仿真实验结果表明:该算法能够获得很高的嵌入率,且具有很好的隐蔽性。

关键词: 计算机应用; 信息安全; 可逆数据隐藏; 图像梯度

中图分类号:TP309.2 文献标志码:A 文章编号:1671-5497(2016)06-2074-06

Adjustable reversible data hiding algorithm with large embedded capacity based on image gradient prediction

HAN Jia-ling^1,², ZHAO Xiao-hui¹

1.College of Communication Engineering, Jilin University, Changchun 130012,China

2.School of Management Science and Information Engineering, Jilin University of Finance and Economics, Changchun 130117,China

Abstract

The image gradient prediction method is applied to select and predict the trend of each pixel's gradient. The, the pixel's value is predicted according to the gradient and adjacent pixels. The use of the reversible data hiding algorithm based on prediction error can effectively reduce the prediction error and improve the hiding capacity. Moreover, in the hiding process, the embedding rule is adjusted to reduce the distortion to the host image. Experimental results show that the proposed algorithm can achieve a very embedding rate and has good concealment.

Key words: computer application; information security; reversible data hiding; image gradient

Show Figures

0 引言

信息安全的理论研究已经成为学术界的热点问题^{[1, 2]}, 其中, 可逆信息隐藏技术是近年来大家关注的焦点。可逆信息隐藏技术要求在接收端不仅能够提取出秘密信息, 还能够完全无损地恢复原载体图像, 具有一般隐藏技术所没有的特点。可逆信息隐藏技术发布的图像是经过修改后的失真图像, 因此即使遭受到信号处理攻击, 在攻击者不知道算法和恢复密钥的情况下也无法得到原始图像, 可逆信息隐藏技术可以用来进行图像认证和版权保护。

近些年来涌现了大量关于可逆信息隐藏技术的理论和成果, 绝大多数技术都基于图像的空间域, 这是因为空间域的方法计算简单, 并且相比于变换域对溢出的处理更加容易。2001年Fridrich等^{[3, 4]}提出了利用图像的最低有效位来隐藏信息的方法, 该方法首先对最低有效位进行压缩, 然后利用压缩后产生的空闲空间进行嵌入处理。Ni等^[5]于2006年提出了基于图像直方图修改的可逆隐藏方法, 该方法通过调整图像直方图的零点或最低点处像素的灰度值, 将秘密数据嵌入到图像中。此类直方图调整的方法^{[6, 7, 8, 9, 10]}能够获得高质量的图像质量, 但缺点是可嵌入的容量受到零点像素数量的限制。

基于预测误差^{[11, 12]}的方法也是可逆数据隐藏中的一个重要部分。Tseng等^[13]于2009年提出了一种不需要使用定位图, 只使用嵌入后像素与预测值之间的误差便能提取出秘密信息的方法。Lee等^[14]在Tseng的基础上提出了可调节的可逆数据隐藏方法, 该方法通过对预测误差的调整提高了嵌入信息的容量。

本文在Lee算法的基础上, 提出了一种改进的大容量可逆数据隐藏方法。该方法利用图像梯度预测方法增加预测准确性, 改进了嵌入方案, 并根据待隐藏数值自适应修改原图像, 从而减少了对原图的修改, 增加了秘密信息的隐蔽性。

1 可逆数据隐藏方法

1.1 图像梯度预测

图像中相邻像素点之间互相关联, 相邻像素具有一定的变化趋势。为了能使预测的像素值更加准确, 本文使用基于梯度选择的预测方法, 通过对预测点的相邻像素值进行测量、计算和比较, 分别计算出该点水平方向、竖直方向以及45° 、-45° 方向的梯度趋势, 并根据梯度趋势进行预测, 以此提高预测的准确性。

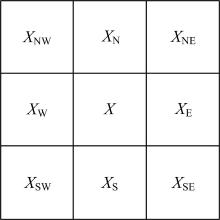
	Figure Option View Download New Window
	图1 根据点X周边的像素预测Fig.1 Prediction of pixel X

具体方法如下:如果要预测图1中点X的像素值, 利用与X相邻共8个点进行判断预测, 首先计算评判4个方向的标准D_i, i=1, 2, 3, 4。

水平方向:

$\begin{matrix} \begin{matrix} D_{1} = (|X_{N} - X_{NW}| + |X_{N} - X_{NE}| + |X_{W} - X| + \\ |X - X_{E}| + |X_{S} - X_{SW}| + |X_{S} - X_{SE}|) / 6 \end{matrix} \end{matrix}$ $\begin{matrix} \begin{matrix} D_{1} = (|X_{N} - X_{NW}| + |X_{N} - X_{NE}| + |X_{W} - X| + \\ |X - X_{E}| + |X_{S} - X_{SW}| + |X_{S} - X_{SE}|) / 6 \end{matrix} \end{matrix}$ (1)

竖直方向:

$\begin{matrix} \begin{matrix} D_{2} = (|X_{W} - X_{NW}| + |X_{W} - X_{SW}| + |X - X_{N}| + \\ |X - X_{S}| + |X_{E} - X_{NE}| + |X_{E} - X_{SE}|) / 6 \end{matrix} \end{matrix}$ $\begin{matrix} \begin{matrix} D_{2} = (|X_{W} - X_{NW}| + |X_{W} - X_{SW}| + |X - X_{N}| + \\ |X - X_{S}| + |X_{E} - X_{NE}| + |X_{E} - X_{SE}|) / 6 \end{matrix} \end{matrix}$ (2)

45° 方向:

$\begin{matrix} \begin{matrix} D_{3} = (|X_{W} - X_{N}| + |X - X_{SW}| + |X - X_{NE}| + \\ |X_{S} - X_{E}|) / 4 \end{matrix} \end{matrix}$ $\begin{matrix} \begin{matrix} D_{3} = (|X_{W} - X_{N}| + |X - X_{SW}| + |X - X_{NE}| + \\ |X_{S} - X_{E}|) / 4 \end{matrix} \end{matrix}$ (3)

-45° 方向:

$\begin{matrix} \begin{matrix} D_{4} = (|X_{N} - X_{E}| + |X - X_{NW}| + |X - X_{SE}| + \\ |X_{S} - X_{W}|) / 4 \end{matrix} \end{matrix}$ $\begin{matrix} \begin{matrix} D_{4} = (|X_{N} - X_{E}| + |X - X_{NW}| + |X - X_{SE}| + \\ |X_{S} - X_{W}|) / 4 \end{matrix} \end{matrix}$ (4)

从式(1)~(4)可以看出, D_i数值越小表示点X更接近这个梯度方向。在得出的D₁~D₄中, 最小值最能代表点X的变化趋势, 使用该方向预测更加准确。因为图像的变化趋势大多数时候较为复杂, 如果仅用一个方向进行预测可能会丢失部分信息, 导致预测准确度降低, 所以为了增加预测的准确性, 选取D值最小的两个方向同时进行预测。

将所有D值从小到大排序, 得到序列{MIN1, MIN2, MIN3, MIN4}。P_MIN1为MIN1对应梯度所在像素, P_MIN2为MIN2对应梯度所在像素, 则有:

$\begin{matrix} X_{pre} = round (\frac{MIN 1}{MIN 1 + MIN 2} P_{MIN 2} + \frac{MIN 2}{MIN 1 + MIN 2} P_{MIN 1}) (5) \end{matrix}$ $\begin{matrix} X_{pre} = round (\frac{MIN 1}{MIN 1 + MIN 2} P_{MIN 2} + \frac{MIN 2}{MIN 1 + MIN 2} P_{MIN 1}) (5) \end{matrix}$

式中:round(· )表示四舍五入计算。

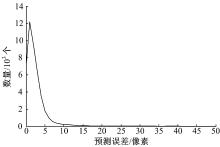
以Lena图像为例, 对预测误差的计算和统计结果如图2所示。

	Figure Option View Download New Window
	图2 预测误差Fig.2 Prediction error

从图2中可以看出, 图中的大部分点都集中在图的左侧, 这表明大部分像素点预测误差都比较小, 符合设计要求。

1.2 数据隐藏方案

Lee等^[14]提出了可调整的可逆数据隐藏方法, 该方法通过对预测误差的调整提高了嵌入数据的容量, 但该方法并没有考虑到秘密信息的值对算法的影响。例如, 无论秘密信息的值是0还是1, 都会使宿主图像发生改变, 造成失真。本文在Lee算法的基础上, 改进隐藏规则, 降低对宿主图像的破坏, 增加图像的不可感知性, 并引入图像梯度预测方法增加预测的准确性, 扩大隐藏信息容量, 有效地提高了信息隐藏的效果。信息隐藏方案的嵌入过程如下:

对宿主图像按照从左至右、从上至下的顺序进行光栅扫描。I(x, y)表示点(x, y)的宿主图像像素值; $\begin{matrix} \hat{I} \end{matrix}$ $\begin{matrix} \hat{I} \end{matrix}$ (x, y)表示用1.1节中梯度预测方法预测的点(x, y)的像素值; 预测误差d用来决定是否嵌入秘密信息; s= $\begin{matrix} \{s |s \in {0, 1}\} \end{matrix}$ $\begin{matrix} \{s |s \in {0, 1}\} \end{matrix}$ 为待嵌入的二值秘密信息。

预测误差d的计算公式为:

$\begin{matrix} d = |I (x, y) - I (x, y)| \end{matrix}$ $\begin{matrix} d = |I (x, y) - I (x, y)| \end{matrix}$ (6)

嵌入规则如下:

规则1 如果d< T, 嵌入秘密信息s。

当I(x, y)≥ $\begin{matrix} \hat{I} \end{matrix}$ $\begin{matrix} \hat{I} \end{matrix}$ (x, y)时,

$\begin{matrix} I_{em} (x, y) = \overset{^{}}{I} (x, y) + d + Ts = I (x, y) + Ts () \end{matrix}$ $\begin{matrix} I_{em} (x, y) = \overset{^{}}{I} (x, y) + d + Ts = I (x, y) + Ts () \end{matrix}$ (7)

当I(x, y)< $\begin{matrix} \hat{I} \end{matrix}$ $\begin{matrix} \hat{I} \end{matrix}$ (x, y)时,

$\begin{matrix} I_{em} (x, y) = \overset{^{}}{I} (x, y) - d - Ts = I (x, y) - Ts () \end{matrix}$ $\begin{matrix} I_{em} (x, y) = \overset{^{}}{I} (x, y) - d - Ts = I (x, y) - Ts () \end{matrix}$ (8)

式中:T为控制嵌入容量的阈值; I_em(x, y)表示嵌入秘密信息后图像在位置(x, y)处的像素值。

。规则2 如果d≥ T, 宿主像素I(x, y)利用下面公式进行调整, 但并不嵌入秘密信息。

当I(x, y)> $\begin{matrix} \hat{I} \end{matrix}$ $\begin{matrix} \hat{I} \end{matrix}$ (x, y)时,

$\begin{matrix} I_{em} (x, y) = I (x, y) + d + T = I (x, y) + T () \end{matrix}$ $\begin{matrix} I_{em} (x, y) = I (x, y) + d + T = I (x, y) + T () \end{matrix}$ (9)

当I(x, y)< $\begin{matrix} \hat{I} \end{matrix}$ $\begin{matrix} \hat{I} \end{matrix}$ (x, y)时,

$\begin{matrix} I_{em} (x, y) = I (x, y) - d - T = I (x, y) - T () \end{matrix}$ $\begin{matrix} I_{em} (x, y) = I (x, y) - d - T = I (x, y) - T () \end{matrix}$ (10)

这里在嵌入方式上进行了改进。对比Lee算法, 当d满足条件进行秘密信息的嵌入时, 无论s的取值是1还是0, 嵌入秘密信息时对原图像都产生了改变。而在改进算法中, 只有当s值取1的时候才改变原像素值, 当s值取0时, I_em(x, y)=I(x, y)± Ts=I(x, y)相当于保留原图像像素值不变, 不产生任何的图像变化和失真, 对秘密信息嵌入的不可见性可产生更好的效果, 在保证不可见性的前提下, 隐藏更多容量的秘密信息。

1.3 提取和恢复方案

在提取秘密信息和恢复原图像的过程中, 与嵌入过程的扫描顺序相反, 使用从右至左、从下至上的顺序。与嵌入时使用的预测方法一样, 计算每一个像素点的预测值 $\begin{matrix} \hat{I} \end{matrix}$ $\begin{matrix} \hat{I} \end{matrix}$ (x, y)以及预测误差d':

$\begin{matrix} d' = |\hat{I} (x, y) - I_{em} (x, y)| () \end{matrix}$ $\begin{matrix} d' = |\hat{I} (x, y) - I_{em} (x, y)| () \end{matrix}$ (11)

用得到的预测误差d'来判断是否包含秘密信息, 并恢复原图像。

规则1 如果d'< 2T, 表示此位置需要提取秘密信息。

当I_em(x, y)≥ $\begin{matrix} \hat{I} \end{matrix}$ $\begin{matrix} \hat{I} \end{matrix}$ (x, y)时,

$\begin{matrix} \{\begin{matrix} 若 d' < T, 那么 I (x, y) = \hat{I} (x, y) + d' = \\ I_{em} (x, y), s = 0 \\ 若 T \leq d' < 2 T, 那么 I (x, y) = \hat{I} (x, y) + \\ d' - T = I_{em} (x, y) - T, s = 1 \end{matrix} () \end{matrix}$ $\begin{matrix} \{\begin{matrix} 若 d' < T, 那么 I (x, y) = \hat{I} (x, y) + d' = \\ I_{em} (x, y), s = 0 \\ 若 T \leq d' < 2 T, 那么 I (x, y) = \hat{I} (x, y) + \\ d' - T = I_{em} (x, y) - T, s = 1 \end{matrix} () \end{matrix}$ (12)

当I_em(x, y)< $\begin{matrix} \hat{I} \end{matrix}$ $\begin{matrix} \hat{I} \end{matrix}$ (x, y)时,

$\begin{matrix} \{\begin{matrix} 若 d' < T, 那么 I (x, y) = \hat{I} (x, y) + d' = \\ I_{em} (x, y), s = 0 \\ 若 T \leq d' < 2 T, 那么 I (x, y) = \hat{I} (x, y) + \\ d' + T = I_{em} (x, y) + T, s = 1 \end{matrix} () \end{matrix}$ $\begin{matrix} \{\begin{matrix} 若 d' < T, 那么 I (x, y) = \hat{I} (x, y) + d' = \\ I_{em} (x, y), s = 0 \\ 若 T \leq d' < 2 T, 那么 I (x, y) = \hat{I} (x, y) + \\ d' + T = I_{em} (x, y) + T, s = 1 \end{matrix} () \end{matrix}$ (13)

规则2 如果d'≥ 2T, 仅恢复原始图像。

$\begin{matrix} I (x, y) = \{\begin{matrix} I_{em} (x, y) - T, I_{em} (x, y) > \hat{I} (x, y) \\ I_{em} (x, y) + T, I_{em} (x, y) < \hat{I} (x, y) \end{matrix} () \end{matrix}$ $\begin{matrix} I (x, y) = \{\begin{matrix} I_{em} (x, y) - T, I_{em} (x, y) > \hat{I} (x, y) \\ I_{em} (x, y) + T, I_{em} (x, y) < \hat{I} (x, y) \end{matrix} () \end{matrix}$ (14)

2 试验结果和分析

为了测试方法的有效性, 对一组灰度图像进行实验。测试图像来自USC-SIPI数据库, 分别为256× 256的8位灰度Lena、Baboon、Barbara、Peppers、Bird、Cameraman、Gold hill和Airplane图像, 用这些图像来观察本文算法在不同图像中的表现。本文所使用的隐藏信息由Matlab仿真软件提供的随机函数生成, 是一个由0和1组成的随机序列。

2.1 不同阈值T对嵌入率和图像质量的影响

采用嵌入后图像与原图之间的峰值信噪比(Peak signal-to-noise ratio, PSNR)评价嵌入秘密信息后对图像的影响, 其计算公式如下:

$\begin{matrix} PSNR = 10 \times \lg \frac{\max (I^{2} (i, j))}{MSE} \end{matrix}$ $\begin{matrix} PSNR = 10 \times \lg \frac{\max (I^{2} (i, j))}{MSE} \end{matrix}$ (15)

式中:MSE为隐藏后图像与原宿主图像之间的均方误差:

$\begin{matrix} MSE = \frac{1}{M \times N} \overset{M}{\sum_{i = 1}} \overset{N}{\sum_{j = 1}} [I (i, j) - I' {(i, j)]}^{2} \end{matrix}$ $\begin{matrix} MSE = \frac{1}{M \times N} \overset{M}{\sum_{i = 1}} \overset{N}{\sum_{j = 1}} [I (i, j) - I' {(i, j)]}^{2} \end{matrix}$ (16)

式中:M、N分别为图像的长和宽; I'(i, j)表示隐藏后的图像。

PSNR的值越大, 表示嵌入后图像与原宿主图像之间的差值越小, 即图像的失真越小。

为了测量隐藏系统中的阈值T对嵌入率和图像质量的影响, 将本文算法应用到不同测试图像中进行比较。阈值T是用来调节嵌入容量的因子, 较小的T带来低嵌入量和较小的失真; 较高的T意味着高嵌入量以及较大的失真。由于T是可以调节的, 所以本文算法中的嵌入率也是可以调节的, 在应用时可根据实际要求进行调整。

从表1中可以看出, 在不同的T值影响下, 嵌入率和嵌入后图像的PSNR值相差较大。并且, 在同样的T值下, 虽然不同图像的PSNR值比较接近, 但还是具有一定差别。比如, Bird图像的PSNR值无论是在T=1, 还是T=5或T=10时, 相比于其他图像都是最大的, 同时Bird中能够嵌入的信息量也是最多的, 这主要由图像本身的特征所决定。因为Bird图像相比于其他图像平滑区块较多, 因此像素间的差值较小。与之相反, Baboon图像纹理特征比较复杂、边缘信息较多、像素点间差值较大, 所以可供嵌入的信息量较少。

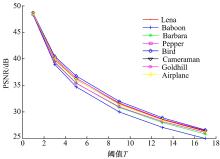
从图3中可以看出, 随着T值的增加, 嵌入后图像的PSNR值呈下降趋势。与从表1中得到的结论一致, 平滑区域较多的Bird图像在同样T值下, 能保持最高的PSNR值, 即嵌入后图像与

表1 不同T值下嵌入对图像的影响 Table 1 Influence on images under different T

	Figure Option View Download New Window
	图3 不同T值下的PSNRFig.3 PSNR obtained under different T

原宿主图像最接近。而与之相反, 复杂纹理较多的Baboon图像, 一直处于同T值下最小PSNR值处, 不仅如此, 结合表1, 在相同T值下, 与其他图像相比, Baboon图像的嵌入量也最少。由此可以得出结论, 图像本身纹理复杂程度对嵌入容量和图像质量有一定影响。

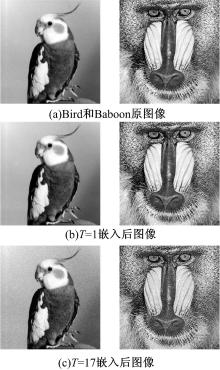
从图4可以看出, 当T=1和T=17时, 嵌入后图像与原图像相比很相近, 并没有发现显著差异。虽然T=17时的PSNR值已经降到30 dB以下, 但是肉眼来看, 失真还比较小, 很难察觉到嵌入后图像与原图像间的差别。

	Figure Option View Download New Window
	图4 不同T值下嵌入后图像与原图像的比较Fig.4 Comparison of embedded images and original images under different T

	Figure Option View Download New Window
	图5 不同T值对嵌入率的影响Fig.5 Influence on embedding rate under different T

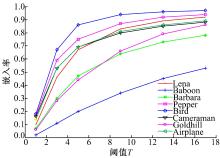
图5是不同T值下所获得的嵌入率变化曲线, 嵌入率与嵌入容量成正比。可以看出, 随着T值的不断增大, 嵌入率呈上升趋势, 且逐渐趋近于1。也就是说, 几乎原图像中大部分像素点都被嵌入了秘密信息, 原宿主图像得到充分利用。与上面对PSNR值的分析类似, 可以看出, 平滑信息较多的Bird图像在同样的T值下能够嵌入更多的秘密信息。相比之下, 对于纹理比较复杂的Baboon图像, 它能够嵌入的秘密信息最少。因此, 综合上面两方面的分析可知, 如果利用本文算法来实现更多、更隐蔽的传输秘密信息, 建议选择平滑信息较多的图像作为宿主图像。这样, 无论在嵌入率还是隐蔽性方面都能获得更好的效果。

2.2 与其他算法比较

本文算法主要有两个方面的改进:一是在预测时使用了基于梯度选择的预测方法, 使预测值更加准确, 从而降低了预测误差。表2是本文算法与Lee算法预测误差的比较, 其中, d为预测误差, 表2中的数值表示满足嵌入条件的像素点个数。像素的数量越多, 表示预测误差越小, 预测越准确。可以看出:本文算法中所获得的像素点要多于Lee算法, 因此可知, 加入方向判断后的梯度选择预测方法能够更加准确地预测像素值, 从而能够嵌入更大容量的秘密信息。二是改进了嵌入方法, 根据隐藏信息的数值和预测误差来决定是否更改原像素, 尽可能减少对宿主图像的修改, 相比于Lee方法对原图像的改变更少, 从而能够获得更高的隐蔽性。表3是在嵌入相同数量的隐蔽信息时, 本文算法与Lee算法的PSNR值比较。从表3中可以看出:在嵌入相同数量的隐藏信息时, 本文算法得到的嵌入后图像PSNR值比Lee算法更高, 也就是说具有更高的隐蔽性。

表2 预测误差比较(个) Table 2 Comparison of prediction error

表3 嵌入同容量隐秘信息时图像质量比较 Table 3 Comparisons of image quality with same embedded capacity dB

上面的实验结果表明, 本文算法无论在嵌入容量还是在隐蔽性方面, 相比于Lee算法, 都获得了更好的效果。并且, 本文算法应用于多个不同图像时, 也具有很好的稳定性。

3 结束语

提出了一种基于图像梯度选择预测的可调节大容量可逆数据隐藏方法, 通过梯度选择来判断待预测点的方向变化趋势, 增加了预测的准确性。在嵌入阶段, 根据隐蔽信息的数值, 尽可能减少对原信息的调整和修改, 加大了嵌入后信息的隐蔽性。本方法使用阈值T来控制嵌入信息量和图像视觉质量。T值较小时, 可得到具有更高隐蔽性和高视觉质量的嵌入后图像; T值较大意味着能够嵌入更多的秘密信息, 但对原图像的改变将增大, 使隐蔽性和视觉质量在一定程度上降低。所以, 嵌入容量和隐蔽性两者相互矛盾, 高嵌入量意味着要牺牲一定的隐蔽性, 而想获得高质量图像就要以一定的嵌入量作为代价。因此, 用户在使用本文算法时, 可根据具体的应用需求来选择阈值T。仿真试验的结果表明, 本文算法无论是在嵌入容量方面, 还是在隐蔽性方面, 都具有很好的应用潜力。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	年桂君, 刘鸿石, 王丹, 等. 彩色照片中隐藏水印信息的分析与实现[J]. 吉林大学学报: 工学版, 2011, 41(1): 339-343. Nian Gui-jun, Liu Hong-shi, Wang Dan, et al. Analysis and realization of watermarking hiding in color picture[J]. Journal of Jilin University(Engineering and Technology Edition), 2011, 41(1): 339-343. [本文引用:1]
[2]	武丹, 汪国昭. 基于差分扩张和差分平移的无损信息隐藏算法[J]. 吉林大学学报: 工学版, 2010, 40(4): 1071-1074. Wu Dan, Wang Guo-zhao. Lossless data hiding based on difference expansion and difference shifting[J]. Journal of Jilin University(Engineering and Technology Edition), 2010, 40(4): 1071-1074. [本文引用:1]
[3]	Fridrich J, Goljan M, Du R. Invertible authentication[C]∥Proceedings of SPIE Photonics West, Security and Watermarking of Multimedia Contents III, San Jose, California, USA, 2001: 197-208. [本文引用:1]
[4]	Fridrich J, Goljan M, Du R. Inversible authentication watermark for JPEG images[C]∥Proceedings of Information Technology: Coding and Computing, Washington, DC, USA, 2001: 223-227. [本文引用:1]
[5]	Ni Z C, Shi Y Q, Ansari N. Reversible data hiding[J]. IEEE Transaetions on Circuits and Systems for Video Teehnology, 2006, 16(3): 354-362. [本文引用:1]
[6]	王俊祥, 倪江群, 潘金伟. 一种基于直方图平移的高性能可逆水印算法[J]. 自动化学报, 2012, 38(1): 88-96. Wang Jun-xiang, Ni Jiang-qun, Pan Jin-wei. A high performance reversible watermarking scheme based on histogram shifting[J]. Acta Automatica Sinica, 2012, 38(1): 88-96. [本文引用:1]
[7]	童学峰, 侯海峰, 宣国荣, 等. 基于直方图对二值图像无损数据隐藏算法的改进[J]. 同济大学学报: 自然科学版, 2011, 39(1): 115-120. Tong Xue-feng, Hou Hai-feng, Xuan Guo-rong, et al. Improvement of reversible binary image data hiding by run-length coding and histogram pair[J]. Journal of Tongji University(Natural Science), 2011, 39(1): 115-120. [本文引用:1]
[8]	Hong W, Chen T S, Wu M C. An improved human visual system based reversible data hiding method using adaptive histogram modification[J]. Optics Communications, 2013, 291: 87-97. [本文引用:1]
[9]	Huang H C, Chang F C. Hierarchy-based reversible data hiding[J]. Expert Systems with Applications, 2013, 40(1): 34-43. [本文引用:1]
[10]	陈莹, 朱明. 多子直方图均衡微光图像增强及FPGA实现[J]. 中国光学, 2014, 7(2): 225-233. Chen Ying, Zhu Ming. Multiple sub-histogram equalization low light level image enhancement and realization on FPGA[J]. Chinese Optics, 2014, 7(2): 225-233. [本文引用:1]
[11]	Leung H Y, Cheng L M, Liu F, et al. Adaptive reversible data hiding based on block median preservation and modification of prediction errors[J]. Journal of Systems and Software, 2013, 86(8): 2204-2219. [本文引用:1]
[12]	Li Jian, Li Xiao-long, Yang Bin. Reversible data hiding scheme for color image based on prediction-error expansion and cross-channel correlation[J]. Signal Processing, 2013, 93(9): 2748-2758. [本文引用:1]
[13]	Tseng H W, Hsieh C P. Prediction-based reversible data hiding[J]. Information Science, 2009, 179(14): 2460-2469. [本文引用:1]
[14]	Lee C F, Chen H L. Adjustable prediction-based reversible data hiding[J]. Digital Signal Processing, 2012, 22(6): 941-953. [本文引用:2]

2011

0.0

. 2011, 41(1):339-343

Analysis and realization of watermarking hiding in color picture

彩色照片中隐藏水印信息的分析与实现

Nian Gui-jun , Liu Hong-shi , Wang Dan

年桂君, 刘鸿石, 王丹

For the watermarking applied in certificate verification,a method that hiding information into pictures in certificate was proposed.Aiming at three main distortions during the process of certificate manufacture,use and verification,the prediction error filter used in L * component of color image's L * a * b * space.A kind of naturally robust watermark pattern is applied to resisting the local and small nonlinear distortion.The bigger geometric distortions are corrected by image registration based on Hausdorff distance.Experimental results show that the proposed method achieves robustness against printing and scanning.

针对利用数字水印技术进行证件真伪鉴别的应用背景,提出一种在证件的彩色照片中隐藏水印信息的方法,通过分析证件上的彩色照片在证件制作、使用以及鉴别过程中经受的三种主要攻击,提出在彩色图像的L * a * b * 颜色空间的L * 亮度分量中嵌入水印,将预测滤波器融于空域水印算法,自然鲁棒的水印模式用于对抗中轻度的几何失真以及局部的、小的非线性几何变形,并采用基于Hausdorff distance的方法校正大的几何失真的水印图像。实验结果表明本文水印算法对打印扫描攻击具有鲁棒性。

... 0 引言信息安全的理论研究已经成为学术界的热点问题^[1,2],其中,可逆信息隐藏技术是近年来大家关注的焦点 ...

2010

0.0

. 2010, 40(4):1071-1074

Lossless data hiding based on difference expansion and difference shifting

基于差分扩张和差分平移的无损信息隐藏算法

Wu Dan , Wang Guo-zhao.

武丹, 汪国昭

基于差分扩张和差分平移提出了一种新的无损信息隐藏算法。在按照一定的顺序扫描图像得到一个灰度序列后,用该算法计算序列中任意2个相邻像素之间的差分,将差分大于K-1(K是由用户根据嵌入容量所选择的一个正整数)的向右扩张,差分小于-K的向左扩张,介于-K、K-1之间的差分用来隐藏信息。并通过适当调整图像灰度使得嵌入信息后差分的改变均匀分布在2个像素上,保证了较好的图像质量。与目前几种常见算法进行比较发现,本文算法在保持相同峰值信噪比的基础上,能够嵌入更多的信息。

... 0 引言信息安全的理论研究已经成为学术界的热点问题^[1,2],其中,可逆信息隐藏技术是近年来大家关注的焦点 ...

2001

0.0

... 2001年Fridrich等^[3,4]提出了利用图像的最低有效位来隐藏信息的方法,该方法首先对最低有效位进行压缩,然后利用压缩后产生的空闲空间进行嵌入处理 ...

2001

0.0

2006

0.0

... Ni等^[5]于2006年提出了基于图像直方图修改的可逆隐藏方法,该方法通过调整图像直方图的零点或最低点处像素的灰度值,将秘密数据嵌入到图像中 ...

2012

0.0

. 2012, 38(1):88-96 DOI:doi:10.3724/SP.J.1004.2012.00088

A high performance reversible watermarking scheme based on histogram shifting

一种基于直方图平移的高性能可逆水印算法

Wang Jun-xiang , Ni Jiang-qun , Pan Jin-wei.

王俊祥, 倪江群, 潘金伟

In recent years, histogram shifting based reversible watermarking has become the domain of extensive research due to its high stego-image quality. Most related schemes are required to transmit extra side information, e.g. peak and zero point pairs, and therefore are non blind in nature. The existing blind schemes, however, exhibit relatively poor performance due to the adoption of fixed peak and zero point pairs. This paper presents a histogram shifting based multi-level embedding scheme for blind reversible watermarking. For single level embedding, a two-step embedding (TSE) approach is proposed, which hides the side information in the stego-image generated with first embedding for blind requirement. While for multi-level embedding, a chain embedding is further incorporated,which ensures both the blind requirement and adoption of optimal peak and zero point pair in each level for high performance reversible watermarking. Extensive simulations are carried out to demonstrate that the proposed scheme could not only achieve the blind reversible watermarking but also outperform other similar ones.

近年来,基于直方图平移的可逆水印算法因其生成水印图像质量高而被广泛研究.目前大部分相关水印算法是非盲的,需要额外传送峰值/零点对等边信息.已有的相关盲水印算法由于采用固定的峰值/零点对而性能较差.本文提出一种面向差值域多层嵌入的高性能直方图平移盲可逆水印算法,有关同步机制可保证在每层嵌入时都选择最优的峰值点和零点.对于单层嵌入,提出两步嵌入法(Two-step embedding,TSE)同步机制,将边信息嵌入到第一步生成的水印像素最低有效位以实现盲提取;对多层嵌入,则进一步提出链式嵌入同步机制,并在最后层采用两步嵌入法以保证水印盲提取.仿真结果表明,本文算法不但可以实现盲提取的要求,而且在算法性能方面较同类算法有显著的提高.

... 此类直方图调整的方法^[6,7,8,9,10]能够获得高质量的图像质量,但缺点是可嵌入的容量受到零点像素数量的限制 ...

2011

0.0

. 2011, 39(1):115-120 DOI:doi:10.3969/j.issn.0253-374x.2011.01.022

Improvement of reversible binary image data hiding by run-length coding and histogram pair

基于直方图对二值图像无损数据隐藏算法的改进

Tong Xue-feng , Hou Hai-feng , Xuan Guo-rong

童学峰, 侯海峰, 宣国荣

The paper presents a novel method which enhances the capability of the reversible binary image data hiding scheme using run length(RL)histogram modification algorithm.Before adopting the reversible binary image data hiding scheme using histogram RL modification algorithm,some pretreatments like AND operation and XOR operation are processed first.Experimental results prove its superiority to other methods.

提出一种改进基于游程编码和直方图对二值无损数据隐藏算法的新方法.先对载体二值图像进行“与”操作或“异或”操作的预处理,再利用基于游程编码的直方图对的二值图像无损数据隐藏方法进行数据嵌入.实验表明,该方法在嵌入容量和视觉效果都优于改进前的方法.

... 此类直方图调整的方法^[6,7,8,9,10]能够获得高质量的图像质量,但缺点是可嵌入的容量受到零点像素数量的限制 ...

2013

0.0

... 此类直方图调整的方法^[6,7,8,9,10]能够获得高质量的图像质量,但缺点是可嵌入的容量受到零点像素数量的限制 ...

2013

0.0

... 此类直方图调整的方法^[6,7,8,9,10]能够获得高质量的图像质量,但缺点是可嵌入的容量受到零点像素数量的限制 ...

2014

0.0

. 2014, 7(2):225-233 DOI:doi:10.3788/CO.20140702.0225

Multiple sub-histogram equalization low light level image enhancement and realization on FPGA

多子直方图均衡微光图像增强及FPGA实现

Chen Ying , Zhu Ming.

陈莹, 朱明

针对微光图像对比度低，目标难以识别的问题，对微光图像增强算法进行了研究。提出了一种多子直方图均衡增强算法，该算法首先将直方图按面积平均分割成4个子直方图，利用平均像素数量作为阈值切割直方图降低过度增强现象，然后加入尺度因子对动态范围进行调整，最后分别对子直方图均衡得到增强效果。此算法用Verilog语言在现场可编程门阵列（ FPGA）上具体实现，并给出了主观和客观的评价，改进算法能产生更清晰的图像，在硬件平台上也能实时显示增强效果，一帧图像处理时延约为0.45 ms。实验结果表明，改进算法不会产生饱和、噪声放大的现象，图像细节保持较好，满足视频图像处理实时性要求，得到了具有较好视觉效果的增强图像。

... 此类直方图调整的方法^[6,7,8,9,10]能够获得高质量的图像质量,但缺点是可嵌入的容量受到零点像素数量的限制 ...

2013

0.0

... 基于预测误差^[11,12]的方法也是可逆数据隐藏中的一个重要部分 ...

2013

0.0

... 基于预测误差^[11,12]的方法也是可逆数据隐藏中的一个重要部分 ...

2009

0.0

... Tseng等^[13]于2009年提出了一种不需要使用定位图,只使用嵌入后像素与预测值之间的误差便能提取出秘密信息的方法 ...

2012

0.0

... Lee等^[14]在Tseng的基础上提出了可调节的可逆数据隐藏方法,该方法通过对预测误差的调整提高了嵌入信息的容量 ...

... 2 数据隐藏方案Lee等^[14]提出了可调整的可逆数据隐藏方法,该方法通过对预测误差的调整提高了嵌入数据的容量,但该方法并没有考虑到秘密信息的值对算法的影响 ...