作者简介:窦慧晶 (1969-),女,副教授,博士.研究方向:阵列信号处理,信号参量估计.E-mail:dhuijing@bjut.edu.cn
针对实际应用的场合中阵元存在取向误差而必须校正的问题,本文基于极化敏感阵列的到达角(DOA)和极化参数估计算法提出了Taylor近似迭代估计方法,即对阵元进行多次一阶Taylor展开估计校正,得到阵列取向误差矩阵。仿真结果表明:该方法得到的校正矩阵对数据校正后DOA和极化参数估计值与信号真实值吻合得很好。
Most existing Direction-of-arrival (DOA) and polarization estimation methods, which are based on polarization sensitive array, generally assume that array element orient the referenced Cartesian coordinates strictly, that is no misorientation. However, in practical applications array elements have misorientations, and it is necessary to calibrate the misorientations. To solve this problem, a Taylor approximate expansion iterative method is proposed. It uses the first-order Taylor approximate expansion to calibrate the array elements repeatedly to get the array's misorientation matrix. The simulation results show that the estimation of DOA and polarization are quite close to the true values by using the proposed method.
信号极化信息是除了信号的幅度、相位和频率等信息之外的另一个可以利用的重要特征, 对包含极化信息在内的信号的多参数估计已经成为近来参数估计研究热点, 并且涌现出大量研究成果[1, 2, 3, 4]。基于极化敏感阵列的信号处理算法都是假设阵列是理想阵列, 即构成阵列的全部电磁矢量传感器(Electromagnetic vector sensor, EMVS)的3个磁偶极子和3个电偶极子的取向是完全相同的。但是在实际环境中, 阵元所对应的通道并不完全平行, 即存在取向误差(也称作原位误差)。当阵元之间存在未知取向误差时, 子空间类方法的分辨性能下降甚至是失效, 因此, 在进行参数估计前, 必须对极化敏感阵列误差进行有效的校正[5]。
针对取向误差校正, 文献[5]根据子空间理论并利用Poynting矢量间的关系估计信号源到达方向和阵列的取向误差矩阵, 但当信噪比偏低或者误差角较大时, 估计精度下降。文献[6]提出了辅助校正补偿的方法。该方法使误差阵元同时接收3个已知DOA、不重叠频谱的校正信号, 然后利用矢量传感器的Poynting矢量求出阵元的误差矩阵, 最后再利用阵列的误差矩阵对阵列实际数据进行补偿, 求出阵列校正后的响应。文献[7]利用一个参数已知的校正源信号校正取向误差, 在实际应用中校正源的DOA很难准确已知。文献[8]利用Taylor近似估计, 当取向误差角较大时估计出阵列的取向误差阵偏差较大。文献[9]提出用3个参量未知的校正源校正方向误差, 比较校正源Poynting矢量在参考阵元与误差阵元的差异构造误差校正矩阵, 但仍然需要较多的校正源。文献[10]基于一阶Taylor近似展开, 提出一种原位误差情况下DOA和极化参数的盲估计算法和各参数估计的CRB界, 文献[9, 10]均以单电磁矢量传感器为研究前提, 需进一步向极化阵列方向推广。针对误差角较大导致估计精度下降的问题, 本文提出了Taylor近似迭代估计算法, 对阵元进行多次校正, 求得阵列的取向误差矩阵。
极化敏感阵列是由多个EMVS构成的阵列。EMVS是由相互正交的3个电偶极子和3个磁偶极子构成的, 能够同时接收到信号的六维电磁场矢量。其结构图如图1所示, 图1中的1, 2, 3表示3个电偶极子; 4, 5, 6表示3个磁偶极子。假设阵列的第一个阵元是参考阵元。
假设有K个窄带, 完全极化电磁波入射, 参考阵元对信号k的响应为:
式中:sk(t)为入射信号k的包络; n(t)为高斯白噪声; α k为极化-角度导向矢量, 如式(2)所示。
式中:D=
θ k∈ [0, π ]为信号k的俯仰角, φ k∈ [0, 2π ]为信号k的方位角; γ k∈ [0, π /2]信号k的极化辅角; η k∈ [-π , π ]为信号k的极化相位差。
信号k的Poynting矢量定义为:
式中:ek为电场矢量;
由于实际阵列在使用环境中的不良因素及EMVS制作工艺, 都可能导致3个电偶极子和3个磁偶极子不能严格地指向三个坐标轴, 形成取向误差。假设阵元l和参考阵元的方向不一致, 即相对于原坐标(x, y, z)取向误差角是(α l, β l)。可以把阵元l的取向误差看作如下变换:将阵元l绕着z轴逆时针旋转α l, 然后再绕x轴逆时针旋转β l, 形成新坐标轴(xl, yl, zl)[9]。误差阵元结构图如图2所示。
信号的极化-角度导向矢量为:
式中:Rl为阵元l旋转矩阵;
M个EMVS以理想的方式排列构成极化敏感阵列, K个完全极化的横向电磁波入射到阵列。阵元l的位置是(x, y, z), 对入射信号k来说阵元l的空间相位因子为:
t时刻阵列输出表示为:
式中:⊗表示Kroneck乘积; A为6M× K维的阵列导向矢量矩阵; N(t)为6M× 1维加性高斯白噪声; λ k为第k个信号的波长; 当q(θ k, φ k)为常数1时, 上述模型退化为单个EMVS的数据模型。
阵列中存在误差阵元, 即误差阵元的排列和参考阵元之间存在偏差, 由式(4)可以得出, 误差阵元对电磁波的响应可以看作是阵元误差矩阵和参考阵的响应乘积[10]。第一个阵元为参考阵元, 阵列存在误差时的响应可以表示成:
R为阵列取向误差矩阵, 6M× 6M维矩阵; Z(t)为理想阵列接收数据; I6为6× 6维的单位矩阵。由于阵元存在取向误差, 实际得到的采样数据
误差校正算法主要在于获得误差矩阵, 对其进行求逆运算进而得到校正矩阵。文献[5, 7]对旋转矩阵在(0, 0)处进行一阶Taylor展开, 但需要参量已知的校正源, 通过确定参数得到误差矩阵, 当参数未知时导致误差校正算法失效。文献[6, 8, 10]校正源参量未知, 对旋转矩阵Rl在(0, 0)处进行一阶Taylor展开, 通过参考阵元和误差阵元的Poynting矢量关系得到误差矩阵。文献[9]用3个参量未知的校正源校正方向误差, 比较校正源Poynting矢量在参考阵元与误差阵元的差异构造误差校正矩阵。除文献[5, 7]外算法校正源参量均未知, 但可通过协方差矩阵特征值分解, 信号子空间和A构成子空间相同, 得到校正源在参考阵元和误差阵元的估计导向矢量, 根据电场、磁场和Poynting矢量关系, 求得校正源Poynting矢量。即校正源参量未知与否, 对误差估计影响不大。
一个参量未知的校正源信号从远场入射到参考阵元上, t和t+Δ t时刻在采样处分别得到采样数据:
根据文献[4]估计得出校正源信号的Poynting矢量为p; 根据同样的方法得到待校正阵元l的Poynting矢量p(l), 根据文献[8]提出的估计方法, 可以由参考阵元l和待校正阵元分别估计信号Poynting矢量, 由式(4)可知:
一般来说, 电磁矢量传感器的阵元的取向误差角(α l, β l)在实际情况中是未知的, 但是在(0, 0)附近范围取值, 根据文献[8]Rl在(0, 0)处进行一阶Taylor近似展开:
由式(18)得:
由式(20)得:
求解上式得出:
将Δ α 和Δ β 代入式(19), 可以得到阵元l近似取向误差矩阵
文献[8]中采用一阶Taylor展开要求阵元的取向误差角(α l, β l)较小, 取向误差角偏大时, 由式(19)得到的
(1)一个参量未知的校正源信号从远场入射待校正阵列, 参考阵元采样数据z1(t), z1(t+Δ t); 误差阵元l采样数据zl(t), zl(t+Δ t), 阵元l的误差矩阵初始值
(2)求出参考阵元p和误差阵元p(l), 根据式(18)和(20)求出
(3)阵元l误差矩阵
(4)判断α l和β l值是否均接近0, 接近时停止循环, 不接近时用
(5)重复步骤(2)直到循环结束; 最终得到阵元l的误差矩阵
(6)按照上述方法逐个校正其他阵元, 根据式(15)得到阵列取向误差矩阵R。其逆矩阵R-1为阵列的校正矩阵列的校正矩阵。R-1乘以阵列接收到的待估计信号数据, 根据文献[11, 12]的方法估计DOA和极化参数。
实验中采用的极化敏感阵列是由3个EMVS构成的均匀线阵, 阵元间距是信号波长的一半。第二个阵元为误差阵元。待估计的信号为两个非相干远场非高斯窄带信号, 信号到达角和极化角分别是[θ 1, φ 1, γ 1, η 1]=(30.93° , 37.09° , 45° , 90° )和[θ 2, φ 2, γ 2, η 2]=(50.08° , 39.71° , 40° , 70° ), 噪声为加性高斯白噪声, 信噪比为20 dB, 快拍数为512。
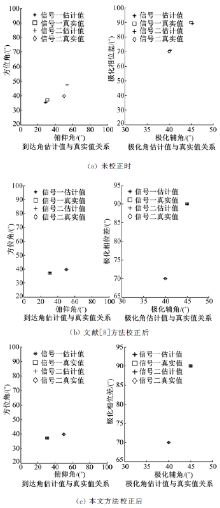
实验一:取向误差角α =3° , β =4° , 信噪比SNR=20 dB, 采样点数为512。未对采样数据进行校正, DOA和极化参数估计值与真实值关系如图3(a)所示。
实验二:实验条件同实验一, 采用文献[8]方法对采样数据进行校正后DOA和极化参数估计值与真实值的关系如图3(b)所示; 采用本文算法校正后DOA和极化参数估计值与真实值的关系如图3(c)所示; 表1给出了取向误差角α =3° , β =4° 两种方法校正后信号1的DOA和极化参数估计值。
| 表1 α =3° , β =4° , 校正后信号1参数估计比较 Table 1 α =3° , β =4° , comparison of parameters estimation of signal 1 after calibration |
实验三:取向误差角α =10° , β =8° , 信噪比SNR=20 dB, 采样点数为512。未对采样数据进行校正, DOA和极化参数估计值与真实值的关系如图4(a)所示。
实验四:实验条件同实验三, 采用文献[8]方法对采样数据进行校正后DOA和极化参数估计值与真实值的关系如图4(b)所示; 用本文算法校正后DOA和极化参数估计值与真实值的关系如图4(c)所示; 表2给出了取向误差角α =10° , β =8° 两种方法校正后信号1的DOA和极化参数估计值。
| 表2 α =10° , β =8° , 校正后信号1参数估计比较 Table 2 α =10° , β =8° , comparison of parameters estimation of signal 1 after calibration |
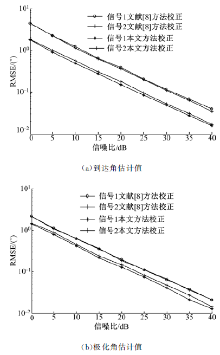
实验五:取向误差α =10° , β =8° , 每个信噪比下做50次独立实验。本文方法校正与文献[8]方法校正后的DOA和极化角度估计值RMSE的关系如图5(a)和(b)所示。
对比实验一结果图3(a)与实验三结果图4(a), 可以看出阵元存在取向误差时对DOA和极化参数估计的影响, 而且取向误差角越大, DOA和极化参数的估计值和实际值偏离越大。
实验二验证了在取向误差角较小情况下文方校正方法的准确性。对比实验二的结果图3(b)和(c)可知, 当取向误差较小时, 文献[8]方法校正后, DOA和极化参数的估计值与实际值偏离不大; 本文方法校正后, DOA和极化参数估计均值接近实际值, 与文献[8]校正方法相比, 估计精度更高。由此说明, 当取向误差角较小时, 旋转矩阵在(0, 0)处Δ α 、Δ β 所取的角度也较小, 在Taylor展开过程中剩下的余项同样较小, 迭代次数降低, 因此两种算法估计精度相差不大。
在较小情况下应用一阶Taylor也可以达到估计精度要求。
实验四验证了本文方法在取向误差角度较大情况子下仍然能正确校正采样数据, 对比实验四的结果图4(b)和(c)可知, 当阵元的取向误差角较大时文献[8]方法校正后, DOA和极化参数的估计值与实际值偏离较大, 而本文方法校正后, DOA和极化参数的估计值更接近实际值, 估计精度大大提高。
对比实验二表(1)与实验四表(2)可知, 本文算法估计出的阵列取向误差矩阵受取向误差角影响不大, 两种误差角度情况下得到的校正矩阵校正待测信号后, 都能准确地估计出DOA和极化参数。
实验五验证了本文方法校正的稳健性, 由实验五的结果图5(a)和(b)看出, 在不同信噪比下本文方法校正DOA和极化参数估计性能明显优于文献[8]校正后, 并且随着信噪比的增大, 到达角和极化角的RMSE急剧减少, 验证了本文校正方法的稳健性。
对比上述实验结果, 可以看出, 当偏差角度较小时, 本文提出算法相对于文献[8]算法在精度上、计算量和收敛速度上相差不大。但当偏差角度较大时, 本文提出方法有了明显的提升。本文采用Taylor近似迭代估计方法估计阵元取向误差, 当误差角度偏差大时, 多次应用Taylor一阶近似估计, 虽然在计算量上有些增加, 但误差角度估计性能有明显提高。
采用Taylor近似迭代估计方法估计阵列的取向误差矩阵, 该方法只需一个参量未知的校正源信号, 估计的阵列取向误差矩阵受取向误差角度影响不大, 取向误差角度较小和较大时, 均能正确校正待测信号, 大大提高了DOA和极化参数估计的精度。随着信噪比的增大, DOA和极化参数的RMSE急剧下降, 证明了本文方法的稳健性。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|