多维DCT/IDCT立体类蝶形算法及其单元式通道结构

引用本文

刘媛媛, 陈贺新, 赵岩, 杨楚皙. 多维DCT/IDCT立体类蝶形算法及其单元式通道结构. 吉林大学学报:工学版, 2016, 46(6): 2094-2102
LIU Yuan-yuan, CHEN He-xin, ZHAO Yan, YANG Chu-xi. Multidimensional DCT/IDCT similar butterfly algorithm and it unit channel architectures. Journal of Jilin University Engineering and Technology Edition, 2016, 46(6): 2094-2102 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201606045
Permissions

多维DCT/IDCT立体类蝶形算法及其单元式通道结构

刘媛媛^1,², 陈贺新¹, 赵岩¹, 杨楚皙¹

1.吉林大学通信工程学院,长春 130012

2.吉林农业大学信息技术学院,长春 130118

赵岩(1971-),女,教授,博士生导师.研究方向:图像与视频编码和立体视频处理.

作者简介:刘媛媛(1980-),女,讲师,博士研究生.研究方向:图像处理与视频编码和立体视频处理.

基金项目:国家自然科学基金项目(61171078,61271315)

摘要

为了匹配离散余弦变换(DCT)算法不同大小分块,实现不同维度DCT结构的兼容性,提出了一种多维DCT立体类蝶形算法,并对其单元式通道结构进行研究。首先,根据DCT理论,以“张量积”运算为基础,介绍了DCT及其反变换IDCT立体类蝶形算法理论原理,给出了多维算法推导。然后,以DCT/IDCT立体类蝶形算法数学运算为理论基础,从一维引申至多维立体类蝶形图形式,并根据多维与一维的关系,以一维单元式通道结构为基础,提出多维单元式通道结构。实验结果表明:本文算法仅需要传统算法中50%的加法器和约30%的乘法器;算法耗时与分块大小和维度有关,在从三维到五维的实验耗时检测中,本文算法耗时不超过普通DCT算法耗时的10%,具有速度快、复杂度低、多维兼容性的特点。

关键词: 信息处理技术; DCT/IDCT; 多维立体; 蝶形算法; 通道式结构

中图分类号:TN919 文献标志码:A 文章编号:1671-5497(2016)06-2094-09

Multidimensional DCT/IDCT similar butterfly algorithm and it unit channel architectures

LIU Yuan-yuan^1,², CHEN He-xin¹, ZHAO Yan¹, YANG Chu-xi¹

1.College of Communication Engineering, Jilin University, Changchun 130012, China

2.College of Information Technology, Jilin Agricultural University, Changchun 130118, China

Abstract

In order to match different size block of Discrete Cosine Transform (DCT) algorithm, the architecture compatibility of different dimensional DCTs is implemented. A multidimensional DCT similar butterfly algorithm is proposed and its unit channel architectures are studied. First, based on the theory of DCT and tensor product operation, the theoretical principles of the DCT similar butterfly algorithm and its inverse transform IDCT are introduced, and the derivation of the multidimensional algorithm is given. Second, taking the arithmetical operation of DCT/IDCT stereo similar butterfly algorithm as the theoretical foundation, the one-dimensional stereo similar butterfly diagram is extended to multidimensional one. Finally, according to the relationship of one-dimension and multi-dimension, based on the one-dimensional channel unit architectures, the multidimensional unit channel architectures are put forward. Experimental results indicate that the proposeds algorithm only needs 50% adders and 30% multipliers of the traditional algorithm. The consuming time of this algorithm is related to the block size and dimension, for three-dimension and five-dimension, the consuming time of this algorithm is less than 10% of that of the common DCT algorithm. This algorithm is characterized by fast, low complexity and multidimensional compatibility.

Key words: information processing; DCT/IDCT; multidimensional stereo; butterfly algorithm; pipeline architectures

Show Figures

0 引言

离散余弦变换(DCT)广泛应用于信息处理领域中, 以其简单的变换算法、高效的变换效果得到人们越来越广泛的关注。当前DCT变换最为有效的应用是高效视频编码(HEVC)^{[1, 2, 3, 4]}和多维矩阵算法^{[5, 6, 7, 8]}。近年来, 对于原理简单的DCT算法, 人们一直追求实现结构简单化、兼容化效果, 其有效途径主要有3个方面:①超大规模集成电路(VLSI)的设计^{[2, 4, 9]}; ②变换核的设计^{[10, 11, 12]}; ③离散余弦正反变换和离散正弦正反变换的兼容结构设计^[13]。而这些结构设计的适用性往往非常局限, 而且当分块、维度等参数变化时, 整体结构的设计也随之变化很大, 甚至不能适用, 这样很难满足当前广泛应用的可变分块、复合编码标准、多维变换等要求。因此, 通道式结构又称管道式结构近年来被人们提及^{[14, 15, 16]}, 通道式结构类似于“ 拼积木” , 只需要设计算法单元结构, 然后根据要求直接给出整体结构。这种方法依托于单元结构, 因此具有极高的兼容性和可延展性。

本文算法充分考虑到算法结构便捷、兼容的特点, 以Nikara和Takala提出的因式分解的DCT算法理论方法^{[15, 16]}为依据, 在此基础上推导出多维DCT算法, 并从快速傅里叶变换(FFT)的蝶形流图中得到灵感, 给出一种立体类蝶形流图形式, 使其复杂定义直观化。同时根据其定义, 提出一种高效、低复杂度、兼容性强的通道式结构, 此种结构可根据需要选择大小, 可塑性强, 思路简单, 实用性、通用性及扩展性极强。

1 DCT/IDCT算法原理

1.1 基础算法及1-D DCT算法原理

本文仅考虑DCT-II型算法, 为了方便, 暂时省略系数 $\begin{matrix} \sqrt[]{2 / N} \end{matrix}$ , 根据参考文献[15], 将DCT变换写成通道式算法结构:

$\begin{matrix} C_{2^{k}} \end{matrix}$ = $\begin{matrix} U_{2^{k}} \end{matrix}$ [ $\begin{matrix} \overset{1}{\prod_{s = k - 1}} \end{matrix} \begin{matrix} Q_{_{2^{k}}}^{s} \end{matrix}$ ( $\begin{matrix} I_{2^{k - s - 1}} \end{matrix} \begin{matrix} {\otimes P}_{2^{s + 1}} \end{matrix}$ )] $\begin{matrix} Q_{_{2^{k}}}^{s} \end{matrix} \begin{matrix} {P^{H}}_{_{2^{k}}} \end{matrix}$ (1)

式中:⊗表示张量积; I为单位矩阵; 2^k=N为进行变换的点数; Q为已知矩阵:

$\begin{matrix} Q_{1} = I_{1}; Q_{2} = I_{2}; Q_{4} = P_{4}^{2}; Q_{N} = I_{N / 4} \otimes Q_{4} \end{matrix}$ (2)

本文均采用基-2的算法, 为了与多维统一, 令 $\begin{matrix} A_{N}^{s} \end{matrix}$ = $\begin{matrix} Q_{N}^{s} \end{matrix}$ ; $\begin{matrix} P_{N}^{H} \end{matrix}$ 和U_N分别为输入和输出排列:

$\begin{matrix} \begin{matrix} {P^{H}}_{N} X = (x_{h_{N} (0)}, x_{h_{N} (1)}, x_{h_{N} (2)}, \dots, x_{h_{N} (N - 1)})^{T} (3) \\ U_{N} = P_{2^{k}} [\overset{k - 3}{\underset{i = 0}{\prod (I_{2^{k - i - 1}} \oplus R_{2^{k} - 2^{k - i - 1}})}} (I_{2^{i + 1}} \otimes P_{2^{k - i - 1}})] \end{matrix} \end{matrix}$ (4)

式中:⊗表示矩阵直和; R为一已知矩阵:

$\begin{matrix} R_{1} = I_{1}; R_{2} = I_{2}; R_{4} = Q_{4} {P^{H}}_{4}; R_{N} = I_{N / 4} \otimes R_{4} \end{matrix}$ (5)

h_N(i)为Hadamard排列函数, 初始值为h₁(0)=0, 分奇偶数定义^[15]为:

$\begin{matrix} \begin{matrix} \{\begin{matrix} h_{2 N} (2 i) = h_{N} (i) \\ h_{2 N} (2 i + 1) = 2 N - 1 - h_{N} (i) \end{matrix} (6) \\ i = 0, 1, \dots, N - 1 \\ 则 : [{P^{H}}_{N}]_{mn} = \{\begin{matrix} 1, n = h_{N} (m) \\ 0, otherwise \end{matrix} (7) \end{matrix} \end{matrix}$

式(1)表示DCT变换中对第s列进行处理, 其中s=0, 1, …, k-1, $\begin{matrix} Q_{_{2^{k}}}^{s} \end{matrix}$ 定义为:

$\begin{matrix} \begin{matrix} Q_{_{2^{k}}}^{s} = M_{_{2^{k}}}^{s} H_{_{2^{k}}}^{s} N_{_{2^{k}}}^{s} F_{2^{k}} (8) \\ M_{_{2^{k}}}^{s} = \overset{2^{k - 1} - 1}{\underset{i = 0}{\oplus}} (\begin{matrix} 1 & 0 \\ - μ_{s} (i) & 1 \end{matrix}) = I_{2^{k - 1}} \otimes (\begin{matrix} 1 & 0 \\ - μ_{s} (i) & 1 \end{matrix}) (9) \\ H_{_{2^{k}}}^{s} = \overset{2^{k - 1} - 1}{\underset{i = 0}{\oplus}} (S_{4} R_{4} S_{4})^{μ_{s - 1} (i)} = I_{2^{k - 2}} \otimes (S_{4} R_{4} S_{4})^{μ_{s - 1} (i)} (10) \\ N_{_{2^{k}}}^{s} = diag (g_{k} (i, s)), i = 0, 1, \dots, 2^{k} - 1 (11) \\ \{\begin{matrix} F_{2} = (\begin{matrix} 1 & 1 \\ 1 & - 1 \end{matrix}) \\ F_{N} = I_{N / 2} \otimes F_{2} \end{matrix} (12) \\ \{\begin{matrix} S_{4} = P_{4} = (\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}) \\ S_{N} = I_{N / 4} \otimes S_{4} \end{matrix} (13) \\ \{\begin{matrix} R_{4} = (\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{matrix}) \\ R_{N} = I_{N / 4} \otimes R_{4} \end{matrix} (14) \end{matrix} \end{matrix}$

函数g_k(i, s)表示为:

$g_{k} (i, s) = {[2^{μ_{s} (⌊\frac{i}{2}⌋)} d (2^{k - s - 1} + ⌊i / 2^{s + 1}⌋)]}^{f_{k} (i, s)} (15)$

式中：

F_k(i, s)=(I mod 2)+(i-τ ₀ (i))(1-τ _k-1(s)) (16)

二进制参数μ _s(· )、τ _i(s)分别定义为:

$\begin{matrix} \begin{matrix} μ_{s} (i) = \{\begin{matrix} 0, imod 2^{n} = 0 \\ 1, imod 2^{n} \neq 0 \end{matrix} (17) \\ τ_{i} (s) = \{\begin{matrix} 0, s = i \\ 1, s \neq i \end{matrix} (18) \end{matrix} \end{matrix}$

系数d(i)按奇偶数可以表示为:

$\begin{matrix} \{\begin{matrix} d (2 i) = \sqrt[]{[1+ d (i)] / 2} \\ d (2 i + 1) = \sqrt[]{[1- d (i)] / 2} \\ d (1) = 1 / 2 \end{matrix} \end{matrix}$ (19)

1-D DCT变换整体写为:

$\begin{matrix} \begin{matrix} X_{D} = U_{N} K_{N} {P^{H}}_{N} x_{D} = \\ \{U_{N} [\overset{1}{\prod_{s = k - 1}} A_{N}^{s} (I_{2^{k - s - 1}} \otimes P_{2^{s + 1}})] A_{N}^{0} {P^{H}}_{N}\} x_{D} (20) \end{matrix} \end{matrix}$

1.2 n-D DCT算法原理

用x_n_D、X_n_D分别表示n维原信号与其正变换的结果, 因此n-D DCT变换定义为:

$\begin{matrix} X_{nD} = \underset{n 个}{\underset{︷}{(C_{N}^{s} \otimes C_{N}^{s} \otimes \dots \otimes C_{N}^{s})}} x_{nD} \end{matrix}$ (21)

根据1-D DCT变换的结果, 得到:

$\begin{matrix} \begin{matrix} X_{nD} = [\underset{n 个}{\underset{︷}{(U_{N} \otimes U_{N} \otimes \dots \otimes U_{N})}} K_{N^{n}} \times \\ \underset{n 个}{\underset{︷}{({P^{H}}_{N} \otimes {P^{H}}_{N} \otimes \dots \otimes {P^{H}}_{N})}}] x_{nD} = \\ U_{N^{n}} K_{N^{n}} {P^{H}}_{N^{n}} x_{nD} (22) \end{matrix} \end{matrix}$

式中: $\begin{matrix} {P^{H}}_{N^{n}} \end{matrix}$ 、 $\begin{matrix} U_{N^{n}} \end{matrix}$ 分别为n-D DCT的输入和输出排列; $\begin{matrix} K_{N^{n}} \end{matrix}$ 为n-D DCT的变换核, 其计算公式为:

$\begin{matrix} \begin{matrix} K_{N^{n}} = [\overset{1}{\prod_{s = k - 1}} \underset{n 个}{\underset{︷}{(Q_{N}^{s} \otimes Q_{N}^{s} \otimes \dots \otimes Q_{N}^{s})}} \times \\ \underset{n 个}{\underset{︷}{(I_{2^{k - s - 1}} \otimes P_{2^{s + 1}}) \otimes (I_{2^{k - s - 1}} \otimes P_{2^{s + 1}}) \otimes \dots \otimes (I_{2^{k - s - 1}} \otimes P_{2^{s + 1}})}}] \times \\ \underset{n 个}{\underset{︷}{(Q_{N}^{0} \otimes Q_{N}^{0} \otimes \dots \otimes Q_{N}^{0})}} (23) \\ 式中 : Q_{N}^{s} \otimes Q_{N}^{s} \otimes Q_{N}^{s} = \\ \underset{n 个}{\underset{︷}{(M_{N}^{s} \otimes M_{N}^{s} \otimes \dots \otimes M_{N}^{s})}} \underset{n 个}{\underset{︷}{(H_{N}^{s} \otimes H_{N}^{s} \otimes \dots \otimes H_{N}^{s})}} \times \\ \underset{n 个}{\underset{︷}{(N_{N}^{s} \otimes N_{N}^{s} \otimes \dots \otimes N_{N}^{s})}} \underset{n 个}{\underset{︷}{(F_{N}^{s} \otimes F_{N}^{s} \otimes \dots \otimes F_{N}^{s})}} (24) \end{matrix} \end{matrix}$

对照1-D DCT, n-D DCT与之类似, 只是将变换中一维的M(指变换中的参数)用相应位置的张量积结果 $\begin{matrix} \underset{n 个}{\underset{︷}{M \otimes M \otimes \dots \otimes M}} \end{matrix}$ 代替, 进一步计算得到, 如式(25)所示, 参数 $\begin{matrix} H_{N}^{s} \end{matrix}$ 、 $\begin{matrix} F_{N}^{s} \end{matrix}$ 、 $\begin{matrix} Q_{N}^{s} \end{matrix}$ 、 $\begin{matrix} I_{2^{k - s - 1}} \end{matrix}$ $\begin{matrix} {⊗P}_{2^{s + 1}} \end{matrix}$ 同理。

$\begin{matrix} \begin{matrix} \underset{n 个}{\underset{︷}{M_{N}^{s} \otimes M_{N}^{s} \otimes \dots \otimes M_{N}^{s}}} = \\ (M_{N}^{s} \otimes I_{N^{n - 1}}) (I_{N^{n - 1}} \otimes M_{N}^{s}) = \\ (M_{N^{2}}^{s} \otimes I_{N^{n - 2}}) (I_{N^{n - 2}} \otimes M_{N^{2}}^{s}) = \\ (M_{N^{m}}^{s} \otimes I_{N^{n - m}}) (I_{N^{n - m}} \otimes M_{N^{m}}^{s}) (25) \\ 而 \\ \underset{n 个}{\underset{︷}{(I_{2^{k - s - 1}} \otimes P_{2^{s + 1}}) \otimes (I_{2^{k - s - 1}} \otimes P_{2^{s + 1}}) \times \dots \times (I_{2^{k - s - 1}} \otimes P_{2^{s + 1}})}} = \\ (I_{2^{k - s - 1}} \otimes P_{2^{s + 1}} \otimes I_{2^{(n - 1) k}}) \times \dots \times (I_{2^{(n - 2) k - s - 1}} \otimes P_{2^{s + 1}} \otimes I_{2^{2 k}}) \times \\ (I_{2^{(n - 1) k - s - 1}} \otimes P_{2^{s + 1}} \otimes I_{2^{k}}) (I_{2^{nk - s - 1}} \otimes P_{2^{s + 1}}) (26) \\ 令 A_{N^{n}}^{s} = \underset{n 个}{\underset{︷}{Q_{N}^{s} \otimes Q_{N}^{s} \otimes \dots \otimes Q_{N}^{s}}} = \\ (M_{N}^{s} \otimes I_{N^{n - 1}}) (I_{N^{n - 1}} \otimes M_{N}^{s}) (H_{N}^{s} \otimes I_{N^{n - 1}}) \times \\ (I_{N^{n - 1}} \otimes H_{N}^{s}) D_{N^{n}}^{s} (F_{N} \otimes I_{N^{n - 1}}) (I_{N^{n - 1}} \otimes F_{N}) = \\ (M_{N^{m}}^{s} \otimes I_{N^{n - m}}) (I_{N^{n - m}} \otimes M_{N^{m}}^{s}) (H_{N}^{s} \otimes I_{N^{n - m}}) \times \\ (I_{N^{n - m}} \otimes H_{N^{m}}^{s}) D_{N^{n}}^{s} (F_{N^{m}} \otimes I_{N^{n - m}}) (I_{N^{n - 1}} \otimes F_{N^{m}}) (27) \end{matrix} \end{matrix}$

因而变换核可以写为:

$\begin{matrix} \begin{matrix} K_{N^{n}} = [\overset{1}{\prod_{s = k - 1}} A_{N^{n}}^{s} (I_{2^{k - s - 1}} \otimes P_{2^{s + 1}} \otimes I_{2^{(n - 1) k}}) \times \\ \dots \times (I_{2^{(n - 2) k - s - 1}} \otimes P_{2^{s + 1}} \otimes I_{2^{2 k}}) \times \\ (I_{2^{(n - 1) k - s - 1}} \otimes P_{2^{s + 1}} \otimes I_{2^{k}}) \times (I_{2^{n k - s - 1}} \otimes P_{2^{s + 1}})] A_{N^{n}}^{0} (28) \end{matrix} \end{matrix}$

n-D DCT变换整体写为:

X_n_D={ $\begin{matrix} U_{N^{n}} \end{matrix}$ [ $\begin{matrix} \overset{1}{\prod_{s = k - 1}} \end{matrix} \begin{matrix} A_{_{N^{n}}}^{s} \end{matrix}$ =( $\begin{matrix} I_{2^{k - s - 1}} \end{matrix} \otimes \begin{matrix} P_{2^{s + 1}} \end{matrix} \otimes$

$\begin{matrix} I_{2^{(n - 1) k}} \end{matrix}$ )× …× ( $\begin{matrix} I_{2^{(n - 2) k - s - 1}} \end{matrix} \otimes \begin{matrix} P_{2^{s + 1}} \end{matrix} \otimes \begin{matrix} I_{2^{2 k}} \end{matrix}$ )×

( $\begin{matrix} I_{2^{(n - 1) k - s - 1}} \end{matrix} \otimes \begin{matrix} P_{2^{s + 1}} \end{matrix} \otimes \begin{matrix} I_{2^{k}} \end{matrix}$ )× ( $\begin{matrix} I_{2^{n k - s - 1}} \end{matrix} \otimes$

$\begin{matrix} P_{2^{s + 1}} \end{matrix}$ )] $\begin{matrix} A_{_{N^{n}}}^{0} \end{matrix} \begin{matrix} {P^{H}}_{_{N^{n}}} \end{matrix}$ }x_n_D(29)

式中:x_n_D及其相应的结果X_n_D为Nⁿ矩阵系数组成的列向量。

2 多维立体类蝶形形式

2.1 基本类蝶形形式

根据式(1), 忽略排列因子, 只需考虑[ $\begin{matrix} \overset{1}{\prod_{s = k - 1}} \end{matrix} \begin{matrix} Q_{_{2^{k}}}^{s} \end{matrix}$ ( $\begin{matrix} I_{2^{k - s - 1}} \end{matrix}$ $\begin{matrix} {⊗P}_{2^{s + 1}} \end{matrix}$ )] $\begin{matrix} Q_{_{2^{k}}}^{0} \end{matrix}$ , 其中 $\begin{matrix} Q_{_{2^{k}}}^{0} \end{matrix}$ 及 $\begin{matrix} Q_{_{2^{k}}}^{s} \end{matrix}$ 各个s取值是级联的关系, $\begin{matrix} I_{2^{k - s - 1}} \end{matrix}$ $\begin{matrix} {⊗P}_{2^{s + 1}} \end{matrix}$ 表示级间排列。由式(8)可知, 每级中 $\begin{matrix} M_{_{2^{k}}}^{s} \end{matrix}$ 、 $\begin{matrix} H_{_{2^{k}}}^{s} \end{matrix}$ 、 $\begin{matrix} N_{_{2^{k}}}^{s} \end{matrix}$ 、 $\begin{matrix} F_{_{2^{k}}} \end{matrix}$ 亦为级联关系, 因此仅考虑各个参数的形式及级间排列参数 $\begin{matrix} I_{2^{k - s - 1}} \end{matrix}$ $\begin{matrix} {⊗P}_{2^{s + 1}} \end{matrix}$ 。由1.1节推导可知, 每级中均由基本蝶形运算、单蝶运算、本级交换、乘数运算完成, 各级间由级联运算和级间排列完成, 需要注意的是, 每级中可能缺少其中的一项或者两项, 如N=8时第一级缺少 $\begin{matrix} M_{8}^{0} \end{matrix}$ 和 $\begin{matrix} H_{8}^{0} \end{matrix}$ , 第二级缺少 $\begin{matrix} H_{8}^{1} \end{matrix}$ , 其原因是此项值恰好为单位矩阵, 向量与其相乘对结果不产生影响。经分析可知整体运算流程恰为DCT流程的倒置形式, 这也符合DCT可逆变换的宗旨, N=8DCT/IDCT类蝶形形式如图1所示, 其中x_i为输入信号; d_i为乘数。

	Figure Option View Download New Window
	图1 N=8点1-D DCT/IDCT类蝶形结构形式Fig.1 N=8 1-D DCT/IDCT similar butterfly architectures

2.2 n-D DCT/IDCT类蝶形形式

n-D DCT变换如式(29)所示, 其中 $\begin{matrix} U_{N^{n}} \end{matrix}$ 、 $\begin{matrix} {P^{H}}_{N^{n}} \end{matrix}$ 为输出、输入排列, 因此仅考虑变换核 $\begin{matrix} K_{N^{n}} \end{matrix}$ , 如式(28)所示, 其中 $\begin{matrix} A_{_{N^{n}}}^{0} \end{matrix}$ 及 $\begin{matrix} A_{_{N^{n}}}^{s} \end{matrix}$ 各个s取值是级联的关系, 根据式(24),

( $\begin{matrix} \underset{n 个}{\underset{︷}{H_{N}^{s} \otimes H_{N}^{s} \otimes H_{N}^{s} \otimes \dots \otimes H_{N}^{s}}} \end{matrix}$ )

( $\begin{matrix} \underset{n 个}{\underset{︷}{M_{N}^{s} \otimes M_{N}^{s} \otimes M_{N}^{s} \otimes \dots \otimes M_{N}^{s}}} \end{matrix}$ )

( $\begin{matrix} \underset{n 个}{\underset{︷}{N_{N}^{s} \otimes N_{N}^{s} \otimes N_{N}^{s} \otimes \dots \otimes N_{N}^{s}}} \end{matrix}$ )

( $\begin{matrix} \underset{n 个}{\underset{︷}{F_{N}^{s} \otimes F_{N}^{s} \otimes F_{N}^{s} \otimes \dots \otimes F_{N}^{s}}} \end{matrix}$ )

类似于一维DCT中参数 $\begin{matrix} M_{_{2^{k}}}^{s} \end{matrix}$ 、 $\begin{matrix} H_{_{2^{k}}}^{s} \end{matrix}$ 、N $\begin{matrix} F_{_{2^{k}}}^{s} \end{matrix}$ 、 $\begin{matrix} F_{2^{k}} \end{matrix}$ 相互间亦为级联关系, n维变换中参数为其自身n-1次张量积运算而成。图2为三维蝶形运算( $\begin{matrix} F_{N}^{s} \end{matrix}$ $\begin{matrix} {\otimes F}_{N}^{s} \end{matrix}$ $\begin{matrix} {\otimes F}_{N}^{s} \end{matrix}$ ), 其中F_N为二维平面中线型蝶形运算, 如图中红色和蓝色蝶形位置, $\begin{matrix} F_{N}^{s} \end{matrix}$ $\begin{matrix} {\otimes F}_{N}^{s} \end{matrix}$ 为三维立体中面型蝶形运算, 如图中红色和蓝色级与黄色级两级级联蝶形位置, $\begin{matrix} F_{N}^{s} \end{matrix}$ $\begin{matrix} {\otimes F}_{N}^{s} \end{matrix}$ $\begin{matrix} {\otimes F}_{N}^{s} \end{matrix}$ 为四维立体中体型蝶形运算, 如全部三级级联蝶形位置。

	Figure Option View Download New Window
	图2 2× 2× 2三维立体蝶形图Fig.2 2× 2× 2 3-D DCT butterfly architectures

n-D DCT变换整体如式(29)所示, 则n-D IDCT变换核为:

$\begin{matrix} \begin{matrix} (C_{N^{n}})^{- 1} = \\ {U_{N^{n}} \cdot [\overset{1}{\prod_{s = k - 1}} A_{N^{n}}^{s} (I_{2^{k - s - 1}} \otimes P_{2^{s + 1}} \otimes I_{2^{(n - 1) k}}) \times \dots \times \\ (I_{2^{(n - 2) k - s - 1}} \otimes P_{2^{s + 1}} \otimes I_{2^{2 k}}) \times I_{2^{(n - 1) k - s - 1}} \times \\ (P_{2^{s + 1}} \otimes I_{2^{k}}) \times (I_{2^{nk - s - 1}} \otimes P_{2^{s + 1}})] A_{N^{n}}^{0} P_{N^{n}}^{H}}^{- 1} (30) \\ 式中 : \\ {[(\underset{n 个}{\underset{︷}{F_{N}^{s} \otimes F_{N}^{s} \otimes F_{N}^{s} \otimes \dots \otimes F_{N}^{s}}})]}^{- 1} \\ {[(\underset{n 个}{\underset{︷}{N_{N}^{s} \otimes N_{N}^{s} \otimes N_{N}^{s} \otimes \dots \otimes N_{N}^{s}}})]}^{- 1} \\ {[(\underset{n 个}{\underset{︷}{H_{N}^{s} \otimes H_{N}^{s} \otimes H_{N}^{s} \otimes \dots \otimes H_{N}^{s}}})]}^{- 1} \\ {[(\underset{n 个}{\underset{︷}{M_{N}^{s} \otimes M_{N}^{s} \otimes M_{N}^{s} \otimes \dots \otimes M_{N}^{s}}})]}^{- 1} \end{matrix} \end{matrix}$

亦为级联关系, 现仅需考虑这4个参数与

( $\begin{matrix} \underset{n 个}{\underset{︷}{F_{N}^{s} \otimes F_{N}^{s} \otimes F_{N}^{s} \otimes \dots \otimes F_{N}^{s}}} \end{matrix}$ )

( $\begin{matrix} \underset{n 个}{\underset{︷}{N_{N}^{s} \otimes N_{N}^{s} \otimes N_{N}^{s} \otimes \dots \otimes N_{N}^{s}}} \end{matrix}$ )

( $\begin{matrix} \underset{n 个}{\underset{︷}{H_{N}^{s} \otimes H_{N}^{s} \otimes H_{N}^{s} \otimes \dots \otimes H_{N}^{s}}} \end{matrix}$ )

( $\begin{matrix} \underset{n 个}{\underset{︷}{M_{N}^{s} \otimes M_{N}^{s} \otimes M_{N}^{s} \otimes \dots \otimes M_{N}^{s}}} \end{matrix}$ )

参数的差异, 得到n-D IDCT与n-D DCT运算形式上的相关性。由上部分参数可知均为1-D DCT相应参数n-1“ 张量积” 后取逆运算而成, 因此n-D IDCT结构结合了n-D DCT与1-D IDCT的特点, 是n维正变换倒置结构情况。

3 通道式结构

3.1 通道式基本结构

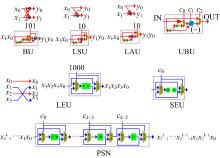
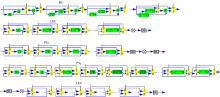
由类蝶形结构形式可知DCT/IDCT包括蝶形单元、乘法单元和交换单元3种基本结构, 如图3所示。统一蝶形单元(UBU)由三个控制量控制输出, 分别得到蝶形操作(BU)、局部减法蝶形操作(LSU)和局部加法蝶形操作(LAU); 交换单元, 又称为移位寄存器(SEU), 作用是进行级内和级间交换。算法过程中分为本级交换单元(LEU)和级间交换单元(PSN)。

	Figure Option View Download New Window
	图3 基本结构示意图Fig.3 Architectures diagram of basic

3.2 n-D DCT基本结构

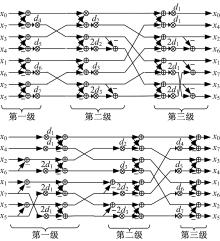
n维BU、LSU、LAU需进行n级蝶形运算, 级间以级联方式连接。第1级为线型蝶形运算, 即为基本蝶形运算; 第2级为面型蝶形运算; 第3级为体型蝶形运算, 以此类推, 将除基本级以外的其他级统称为延时级, 以N=2^k为例, 第2级蝶形运算在基本蝶形运算硬件基础上将原延时器D替换为 $\begin{matrix} (2^{k}) \end{matrix}$ D; 第3级蝶形运算在基本蝶形运算硬件基础上将原延时器替换为 $\begin{matrix} {(2^{k})}^{2} \end{matrix}$ D, 则n级蝶形运算在基本蝶形运算硬件基础上将原延时器替换为 $\begin{matrix} {(2^{k})}^{n - 1} \end{matrix}$ D。UBUⁿ结构单元如图4所示。

n维级间排列如式(26)所示, 在结构中, 仍沿袭基本级与其他延时级级联运算的形式, 若基本级中为两级运算的, 则延时级为对两级运算分别对应进行延时, 延时大小不变。P $\begin{matrix} S_{8}^{n} \end{matrix}$ 结构示意图如图5所示。

	Figure Option View Download New Window
	图4 UBUⁿ结构示意图Fig.4 Architectures diagram of UBUⁿ

	Figure Option View Download New Window
	图5 P $\begin{matrix} {S^{n}}_{8} \end{matrix}$ 结构示意图Fig.5 Architectures diagram of P $\begin{matrix} {S^{n}}_{8} \end{matrix}$

3.3 n-D DCT/IDCT通道式结构

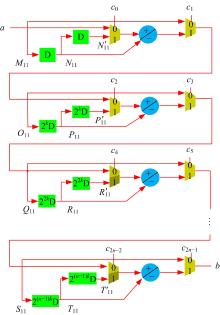
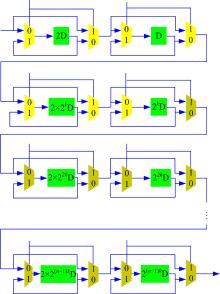
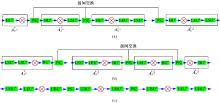
以图4和图5所示结构为基础将其模块化, n-D DCT/IDCT通道式结构如图6(a)(b)所示, 以N=8、k=3为例, 将LSUⁿ、BUⁿ均用UBUⁿ表示, 比较n-D DCT和IDCT两图结构, 将两图合二为一得到n-D DCT/IDCT兼容性通道式结构如图6(c)所示(控制量已省略), 结构器件示意图如图7所示。

	Figure Option View Download New Window
	图6 n-D DCT/IDCT通道式结构Fig.6 n-D DCT/IDCT pipeline schematic architectures

	Figure Option View Download New Window
	图7 N=8点n-D DCT/ IDCT兼容性通道式结构器件示意图Fig.7 N=8 n-D DCT/ IDCT compatible pipeline architectures view of devices

4 复杂度分析

4.1 硬件复杂度分析

由图4可知, n维DCT结构主要由延时器、选择器和乘法器3部分组成。从硬件功能方面上看, n维DCT结构主要由蝶形运算BU(单蝶运算LSU和LEU均归属于蝶形运算范畴)、乘法运算和交换运算PS, 其中乘法运算由乘法器完成, 交换运算由延时器和选择器完成, 每级BU延时器和选择器以外还需要3个加法器(含减法)完成蝶形操作。一个Nⁿ= $\begin{matrix} \underset{n 个}{\underset{︷}{2^{k} \times 2^{k} \times \dots \times 2^{k}}} \end{matrix}$ 点的n维DCT所需延时器主要由两部分组成:

(1)蝶形运算总共需要BUⁿ3(log₂N-1)级, 每级需要延时器个数为:

$\begin{matrix} 2 \times (1 + N + N^{2} + \dots + N^{n - 1}) (31) \end{matrix}$

(2)级间交换P $\begin{matrix} S_{M}^{n} \end{matrix} \begin{matrix} (M = 2^{m}) \end{matrix}$ 需要延时器个数为:

$\begin{matrix} (2^{0} + 2^{1} + 2^{2} + \dots + 2^{m - 2}) (1 + N + N^{2} + \dots + N^{n - 1}) (32) \end{matrix}$

而Nⁿ点n维DCT需要P $\begin{matrix} S_{4}^{n} \end{matrix}$ 、P $\begin{matrix} S_{8}^{n} \end{matrix}$ 、…到P $\begin{matrix} S_{m}^{n} \end{matrix}$ 的(log₂N-1)级级间交换。因此Nⁿ点n维DCT总共需要延时器个数为:

$\begin{matrix} \begin{matrix} [6 (lo g_{2} N - 1) + 2^{0} + (2^{0} + 2^{1}) + \\ (2^{0} + 2^{1} + 2^{2}) + \dots + (2^{0} + 2^{1} + 2^{2} + \dots + \\ 2^{m - 2})] (1 + N + N^{2} + \dots + N^{n - 1}) (33) \end{matrix} \end{matrix}$

类似地, 二选一选择器的个数也由两部分组成:①蝶形运算总共需要BUⁿ3 $\begin{matrix} (lo g_{2} N - 1) \end{matrix}$ 级, 每级需要选择器2n个; ②级间交换需要选择器 $\begin{matrix} [1 + 2 + 3 + \dots + (m - 1)] \end{matrix}$ × 2n个, 因此Nⁿ点n维DCT总共需要二选一选择器数组个数为:

$\begin{matrix} \begin{matrix} [3 (lo g_{2} N - 1) + 1 + 2 + 3 + \dots + \\ (m - 1)] \times 2 n (34) \end{matrix} \end{matrix}$

4.2 计算复杂度分析

n维DCT是一维运算多维化的结果, 其中运算仅为乘法器和加法器, 乘法器是由式(11)产生的, 其中g_k(i, s)是每级的乘数, 值不为1的个数即为乘法器的个数, 一维DCT乘法器的个数为:

$\begin{matrix} \frac{N}{2} lo g_{2} N + 1 (35) \end{matrix}$

n维DCT的乘法运算为:

$\begin{matrix} (\underset{n 个}{\underset{︷}{N_{N}^{(s)} \otimes N_{N}^{(s)} \otimes \dots \otimes N_{N}^{(s)}}}) \end{matrix}$ (36)

由式(36)可以看出, 该运算仅仅改变了每级乘数的不同, 但并没有改变乘法器的级数, 根据张量积的运算规则, 其值为“ 1” 的乘数呈指数增长, 因而n维DCT乘法器的个数为:

$\begin{matrix} N^{n} lo g_{2} N - {(\frac{N}{2})}^{n} (lo g_{2} N - 1) - {(\frac{N}{2} - 1)}^{n} () \end{matrix}$ (37)

加法器来自于蝶形和半蝶形运算, 每个蝶形运算中含有两个加法运算, 每级含有N/2个基本蝶形, 共有k级, 而减法半蝶形运算是每级中每个群少1个, 一个DCT变换共含有减法半蝶形运算个数为:

$\begin{matrix} \begin{matrix} \frac{N}{2} lo g_{2} N - (2^{0} + 2^{1} + \dots + 2^{k - 1}) = \\ \frac{N}{2} lo g_{2} N - N + 1 \end{matrix} \end{matrix}$ (38)

因此一维DCT加法器的个数为:

$\begin{matrix} \frac{3}{2} lo g_{2} N - N + 1 \end{matrix}$ (39)

则n维DCT将每个一维加法(包括减法)运算扩展至n维, 所以n维DCT加法器总个数为:

$\begin{matrix} n N^{n - 1} (\frac{3}{2} lo g_{2} N - N + 1) (40) \end{matrix}$

5 实验结果及分析

根据本文采用的多维DCT/IDCT立体类蝶形算法, 表1针对视频不同分块N× N× N以常见的三维DCT方法为例对完成一个蝶形运算单元所使用加法器和乘法器数量进行比较, 其中算法一为传统快速算法, 算法二为行排列的方法^[17]。表1说明, 对于加法器, 算法二与本文算法相等, 约为算法一的一半, 而对于乘法器仅约为算法一的30%, 约为算法二的60%。可明显看出本文提出的算法节约了大量的影响计算速度的乘法器的数量。

表1 蝶形运算单元所用乘法器和加法器个数对比 Table 1 Comparison of number of multiplication and addition operations in butterfly unit

将视频信号中首帧以行、列像素m× m大小进行分块, 结合这个分块所对应的m帧, 即大小为m× m× m的三维视频块, 同理, 将这样m个大小为m× m× m的三维视频块首尾相连, 得到大小为m× m× m× m的四维视频块, 以此类推, 建立多维信号模型。实验仿真环境为:计算机处理器CPU Intel(R) Core(TM)i3-2120@3.30 GHz, Windows7 32 bit操作系统; 3.17 GB可用内存; Visual C++ 2010软件开发环境。表2为以176× 144 150帧视频信号为例, 不同m、不同维度时本文算法与普通DCT处理视频信号耗时^[18]的实验比较。实验结果表明:①m越大, 本文算法耗时越少; ②m相同情况下, 维度越高, 本文算法耗时越少, 这也正好说明本文算法中“ 张量积” 运算的优势; ③m=4时, 相邻维度耗时降低幅度近似; ④m=8时, 三维和四维算法耗时百分比接近, 这是由于在四维时对应视频信号不能恰好为8的倍数, 而出现了计算冗余, m越大冗余越明显; ⑤m=8时, 五维算法耗时所占百分比最小, 说明该视频信号在对应维度中最为优化。

表2 不同分块及维度本文算法与普通DCT处理视频信号的耗时对比 Table 2 Time needed between ordinary DCT and DCT alogorithm with different block sizes and dimensions

6 结束语

在一维DCT的基础上提出了n维DCT及其反变换IDCT算法及类蝶形运算的算法流程, 同时, 根据流程提出了一种仅由延时器、选择器和乘法器组成的多维DCT/IDCT算法单元通道式结构。提出的类蝶形算法流程将n维运算直观化、立体化。以三维DCT算法为例, 对比实验数据表明, 本文算法仅需要传统算法中一半的加法器和约30%的乘法器, 大大提高了运算速度、降低了运算的复杂度。从不同分块和维度本文算法与普通DCT处理视频信号耗时对比结果可以看出, 算法耗时与分块大小、维度有关, 但在m=4和m=8时, 从三维到五维的实验耗时检测中可以看出, 本文算法耗时不到普通DCT算法耗时的10%; 当m=8时, 五维信号处理176× 144 150帧视频信号仅耗时253 s, 仅为普通DCT算法耗时的1.22%。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Conceicao R, Souza J C, Jeske R, et al. Power efficient and high throughput multi-size IDCT targeting UHD HEVC decoders[C]∥IEEE International Symposium on Circuits and Systems, Melboume, Australia, 2014: 1925-1928. [本文引用:1]
[2]	Sun H M, Zhou D J, Liu P L, et al. A low-cost VLSI architecture of multiple-size IDCT for H. 265/HEVC[DB/OL]. [2014-05-08]. http://www.aoni.waseda.jp/zhou/pdf/ieice/e97-a_12_2467.pdf. [本文引用:2]
[3]	Pastuszak G. Flexible architecture design for H. 265/HEVC inverse transform[J]. Circuits Systems and Signal Processing, 2015, 34(6): 1931-1945. [本文引用:1]
[4]	杨启洲, 刘一清. 基于HEVC的多长度DCT变换的VLSI设计[J]. 微电子学, 2015, 45(1): 102-105. Yang Qi-zhou, Liu Yi-qing. Design of DCT of different lengths VLSI architecture for HEVC[J]. Microelectronics, 2015, 45(1): 102-105. [本文引用:2]
[5]	桑爱军, 穆森, 王墨林, 等. 基于多维矢量矩阵的多视角视频编码[J]. 吉林大学学报: 工学版, 2013, 43(4): 1110-1115. Sang Ai-jun, Mu Sen, Wang Mo-lin, et al. Multi-view video coding based on multi-dimensional vector matrix[J]. Journal of Jilin University(Engineering and Technology Edition), 2013, 43(4): 1110-1115. [本文引用:1]
[6]	孙文邦, 陈贺新, 孙文斌, 等. 基于变换基阵的SDCT 算法[J]. 吉林大学学报: 工学版, 2011, 41(增刊1): 325-331. Sun Wen-bang, Chen He-xin, Sun Wen-bin, et al. SDCT operation based on transform basic matrix[J]. Journal of Jilin University(Engineering and Technology Edition), 2011, 41(Sup. 1): 325-331. [本文引用:1]
[7]	桑爱军, 杨树媛, 赵欣. 基于多维矢量矩阵离散余弦变换的熵编码[J]. 吉林大学学报: 工学版, 2011, 41(增刊1): 319-324. Sang Ai-jun, Yang Shu-yuan, Zhao Xin. Entropy code based on multidimensional vector matrix DCT[J]. Journal of Jilin University(Engineering and Technology Edition), 2011, 41(Sup. 1): 319-324. [本文引用:1]
[8]	赵志杰, 陈贺新, 桑爱军. 三维矩阵可变分割彩色图像压缩编码[J]. 吉林大学学报: 工学版, 2009, 39(1): 194-197. Zhao Zhi-jie, Chen He-xin, Sang Ai-jun. Color image compression based on variable matrix size three dimensional matrix wide DCT[J]. Journal of Jilin University(Engineering and Technology Edition), 2009, 39(1): 194-197. [本文引用:1]
[9]	Huang H, Xiao L Y. CORDIC based fast algorithm for power-of-point DCT and its efficient VLSI implementation[J]. Microelectronics Journal, 2014, 45(11): 1480-1488. [本文引用:1]
[10]	桑爱军, 王艇, 栾晓利, 等. 2M维矢量余弦整数变换核矩阵[J]. 光学精密工程, 2013, 21(7): 1891-1897. Sang Ai-jun, Wang Ting, Luan Xiao-li, et al. 2M-dimensional vector integer DCT transform kernel matrix[J]. Optics and Precision Engineering, 2013, 21(7): 1891-1897. [本文引用:1]
[11]	Chen Y H, Chen J N, Chang T Y, et al. High-throughput multistand ard transform core supporting MPEG/H. 264/VC-1 using common sharing distributed arithmetic[J]. IEEE Transactions on Very Large Scale Integration (VLSI) System, 2014, 22(3): 463-474. [本文引用:1]
[12]	Chen Y H, Jou R Y, Chang T Y, et al. A high-throughput and area-efficient video transform core with a time division strategy[J]. IEEE Transactions on Very Large Scale Integration (VLSI) System, 2014, 22(11): 2268-2277. [本文引用:1]
[13]	Huang H, Xiao L Y, Liu J M. CORDIC-based unified architecture for computation of DCT/IDCT/DST/IDST[J]. Circuits Systems and Signal Processing, 2014, 33(3): 799-814. [本文引用:1]
[14]	Aggrawal E, Kumar N. High throughput pipelined 2D discrete cosine transform for video compression[C]∥International Conference on Issues and Challenges in Intelligent Computing Techniques, Ghaziabad, India, 2014: 702-705. [本文引用:1]
[15]	Nikara J A, Takala J H, Astola J T. Discrete cosine and sine transforms-regular algorithms and pipeline architectures[J]. Signal Processing, 2006, 86(2): 230-249. [本文引用:3]
[16]	Takala J, Nikara J, Punkka K. Pipeline architecture for two-dimensional discrete cosine transform and its inverse[C]∥Proceedings of the Ninth International Conference on Electronics Circuits Systems, Dubrovnik, Croatia, 2002: 749-750. [本文引用:2]
[17]	Boussakta S, Alshibami H O. Fast algorithm for the 3-D DCT-II[J]. Signal Processing, 2004, 52(4): 992-1001. [本文引用:1]
[18]	Sang A J, Sun T N, Chen H X, et al. 6D vector orthogonal transformation and its application in multiview video coding[J]. The Imaging Science Journal, 2013, 61(4): 341-350. [本文引用:1]

2014

0.0

... 当前DCT变换最为有效的应用是高效视频编码(HEVC)^[1,2,3,4]和多维矩阵算法^[5,6,7,8] ...

2014

0.0

... 当前DCT变换最为有效的应用是高效视频编码(HEVC)^[1,2,3,4]和多维矩阵算法^[5,6,7,8] ...

... 近年来,对于原理简单的DCT算法,人们一直追求实现结构简单化、兼容化效果,其有效途径主要有3个方面:①超大规模集成电路(VLSI)的设计^[2,4,9] ...

2015

0.0

... 当前DCT变换最为有效的应用是高效视频编码(HEVC)^[1,2,3,4]和多维矩阵算法^[5,6,7,8] ...

2015

0.0

. 2015, 45(1):102-105

Design of DCT of different lengths VLSI architecture for HEVC

基于HEVC的多长度DCT变换的VLSI设计

Yang Qi-zhou , Liu Yi-qing.

杨启洲, 刘一清

为了满足下一代视频压缩标准HEVC中定义的四种不同长度DCT变换的要求,提出了一种灵活的DCT变换的VLSI架构。从DCT系数矩阵分解算法推导出可用于不同长度的一维DCT变换的硬件架构,在保持数据吞吐量不变的情况下,能够支持4,8,16,32点等不同长度的DCT变换。采用130nm工艺库综合后,得到电路的最高工作频率为131 MHz,能够支持HEVC标准的4k(4 096×2 048)高清视频进行60帧每秒的编码处理。

... 当前DCT变换最为有效的应用是高效视频编码(HEVC)^[1,2,3,4]和多维矩阵算法^[5,6,7,8] ...

... 近年来,对于原理简单的DCT算法,人们一直追求实现结构简单化、兼容化效果,其有效途径主要有3个方面:①超大规模集成电路(VLSI)的设计^[2,4,9] ...

2013

0.0

. 2013, 43(4):1110-1115 DOI:doi:10.7964/jdxbgxb201304042

Multi-view video coding based on multi-dimensional vector matrix

基于多维矢量矩阵的多视角视频编码

Sang Ai-jun , Mu Sen , Wang Mo-lin

桑爱军, 穆森, 王墨林

摘　要：针对现行视频压缩编码标准对多视角视频编码（MVC）的支持与扩展存在一定的局限性这一问题,结合多维矢量矩阵理论,对先前研究中提出的针对单一视角彩色视频流的一整套压缩编码方案加以扩展,将其应用于八个视角的视频编码中,包括多维分块、多维重组、多维矢量DCT正交变换、多维量化、差分编码、多维扫描及行程编码。通过对实验数据的分析,验证了这一整套方案在多视角视频编码中的可行性,为多维矢量矩阵以及多视角视频编码的进一步研究奠定了基础。

... 当前DCT变换最为有效的应用是高效视频编码(HEVC)^[1,2,3,4]和多维矩阵算法^[5,6,7,8] ...

2011

0.0

. 2011, 41(增刊1):325-331

SDCT operation based on transform basic matrix

基于变换基阵的SDCT 算法

Sun Wen-bang , Chen He-xin , Sun Wen-bin

孙文邦, 陈贺新, 孙文斌

Facing the 1-D DCT,2-D DCT and 3-D DCT haven't unified mathematical expression,and multidimensional DCT operation is accomplished by computing 1-D DCT to each dimension of 3-D data successively,which cannot embody the overall space character of multidimensional transformation well.To overcome such drawbacks,a new SDCT method was proposed.First,several matrix operation methods were defined.Then,the operation principle of 1-D DCT,2-D DCT and 3-D SDCT was described in detail.Finally,the performance of SDCT was described.The theoretical analysis shows that the SDCT makes DCT unified and succinct to express,easy to comprehend and convenient to operate.

各维DCT没有统一的矩阵表达式,特别是多维DCT运算,都是对各个维度分别进行一维DCT来完成,这种运算方法不能很好地体现多维变换的整体空间特性。为克服这一问题,提出了一种SDCT运算方法。首先,定义了几种新的矩阵运算;其次,详细描述了一维SDCT、二维SDCT和三维SDCT的运算原理;最后,对SDCT性能进行了讨论。理论分析表明:SDCT使DCT具有统一简洁的表达式、理解容易、计算便捷。

... 当前DCT变换最为有效的应用是高效视频编码(HEVC)^[1,2,3,4]和多维矩阵算法^[5,6,7,8] ...

2011

0.0

. 2011, 41(增刊1):319-324

Entropy code based on multidimensional vector matrix DCT

基于多维矢量矩阵离散余弦变换的熵编码

Sang Ai-jun , Yang Shu-yuan , Zhao Xin.

桑爱军, 杨树媛, 赵欣

Run length-Huffman coding(RL-VLC) in JPEG is normally used as entropy coding method for multi-dimensional vector matrix discrete cosine transform(MD-VMDCT).However it can not effectively compress image since there are lots of long run length of quantized coefficients after three-dimensional scan,here an improved RL-VLC coding method was proposed.According to the Huffman code table which is designed by the probability distributions of level and run level combination,this algorithm achieved entropy coding for color image.Experimental results show that the compression efficiency of proposed algorithm is better than traditional Huffman coding,in the case of the same PSNR,the proposed algorithm saves bit rate at least 9%,much better than JPEG,and there are good prospects for the application of higher-dimensional video frames compression.

针对传统JPEG中游程-霍夫曼熵编码方法在彩色图像的多维矢量矩阵离散余弦变换体系中,不能充分有效压缩数据的问题,提出了一种根据非零交流系数幅值尺寸和该系数前零游程长度尺寸的联合分布进行游程编码,再进行霍夫曼编码的新方法,并重新统计设计了霍夫曼码表。实验结果表明:该方法的压缩性能较改进前熵编码,在PSNR相同的情况下,比特率至少降低了9%,远优于JPEG方法,在更高维的视频图像变换压缩中有着良好的应用前景。

... 当前DCT变换最为有效的应用是高效视频编码(HEVC)^[1,2,3,4]和多维矩阵算法^[5,6,7,8] ...

2009

0.0

. 2009, 39(1):194-197 DOI:doi:10.3321/j.issn:0372-2112.2002.04.037

Color image compression based on variable matrix size three dimensional matrix wide DCT

三维矩阵可变分割彩色图像压缩编码

Zhao Zhi-jie , Chen He-xin , Sang Ai-jun.

赵志杰, 陈贺新, 桑爱军

针对基于三维矩阵宽离散余弦变换的彩色图像压缩方法通常采用的固定尺寸的子阵分割方案和固定尺寸的变换编码.由于图像的不同区域具有不同的统计特性,故采用固定尺寸的分割方案不能有效利用图像本身的相关性,提出了一种三维矩阵可变分割的彩色图像压缩编码方法.该方法采用可变分割的子阵分割方案和变尺寸三维矩阵宽离散余弦变换.首先计算图像的活动性,根据图像活动性的大小将被编码图像划分成不同大小的三维子矩阵.对不同大小的子矩阵分别采用相应尺寸的三维矩阵宽离散余弦变换.变换系数采用非均匀标量量化和熵编码.实验结果表明该方法的压缩性能在低比特率时远远优于JPEG方法,在压缩比相同的情况下,PSNR最多有超过2dB的提高,主观质量也有提升.

... 当前DCT变换最为有效的应用是高效视频编码(HEVC)^[1,2,3,4]和多维矩阵算法^[5,6,7,8] ...

2014

0.0

... 近年来,对于原理简单的DCT算法,人们一直追求实现结构简单化、兼容化效果,其有效途径主要有3个方面:①超大规模集成电路(VLSI)的设计^[2,4,9] ...

2013

0.0

. 2013, 21(7):1891-1897 DOI:doi:10.3788/OPE.20132107.1891

2M-dimensional vector integer DCT transform kernel matrix

2M维矢量余弦整数变换核矩阵

Sang Ai-jun , Wang Ting , Luan Xiao-li

桑爱军, 王艇, 栾晓利

To reduce the computation time of multidimensional data processing, a 2 M-dimensional vector integer Discrete Cosine Transformation(DCT) kernel matrix was proposed and the orthogonality and energy concentration of the integer transform kernel matrix were analyzed. First, according to the theory and properties of original floating-point 2 M-dimensional vector DCT transform kernel matrix, the algorithm for the 2 M-dimensional vector DCT integer transform kernel matrix was introduced and the orthogonality of 2 M-vector integer transform kernel matrix was validated. Then, the basic principles of blocking and reorganizing the *.yuv format video files were given. Finally, by taking the four order and eight order integer transform kernels as examples, the 2 M-dimensional vector integer transform kernel matrix was analyzed, namely, the energy concentration of multidimensional data after integer transform was discussed. The experimental results show that 2 M-vector transform relative floating-point transformation has good energy concentration. The average value of energy concentration for the Y component has reached more than 97.3%, and those for the U component and V component have been more than 99.9%. It concludes that the results will provide a strong basis for compression processing of multi-dimensional data.

为了减少处理多维数据的运算时间，提出了2M维矢量离散余弦变换（DCT）整数核矩阵，并分析了该整数变换核矩阵的正交性和能量集中性。首先，根据原有浮点型2M维矢量DCT变换核矩阵的理论及性质介绍了2M维矢量DCT整数变换核矩阵的实现算法；验证了2M维矢量整数变换核矩阵的正交性。然后，简述了对*.yuv格式视频文件进行分块与重组的基本原理。最后，以四阶整数变换核为例，分析了2M维矢量整数变换核矩阵，即讨论多维数据在整数变换后的能量集中性。实验结果表明：采用2M维矢量整数变换相对浮点型变换仍然具有较好的能量集中性，而且Y分量能量集中性均值已达到97.3%以上，U分量和V分量的能量集中性均值也已达到99.9%以上，此结果会对后来的多维数据压缩编码处理提供有力依据。

... ②变换核的设计^[10,11,12] ...

2014

0.0

... ②变换核的设计^[10,11,12] ...

2014

0.0

... ②变换核的设计^[10,11,12] ...

2014

0.0

... ③离散余弦正反变换和离散正弦正反变换的兼容结构设计^[13] ...

2014

0.0

... 因此,通道式结构又称管道式结构近年来被人们提及^[14,15,16],通道式结构类似于#cod#x0201c ...

2006

0.0

... 因此,通道式结构又称管道式结构近年来被人们提及^[14,15,16],通道式结构类似于#cod#x0201c ...

... 本文算法充分考虑到算法结构便捷、兼容的特点,以Nikara和Takala提出的因式分解的DCT算法理论方法^[15,16]为依据,在此基础上推导出多维DCT算法,并从快速傅里叶变换(FFT)的蝶形流图中得到灵感,给出一种立体类蝶形流图形式,使其复杂定义直观化 ...

... h_N(i)为Hadamard排列函数,初始值为h₁(0)=0,分奇偶数定义^[15]为: ...

2002

0.0

... 因此,通道式结构又称管道式结构近年来被人们提及^[14,15,16],通道式结构类似于#cod#x0201c ...

2004

0.0

... N以常见的三维DCT方法为例对完成一个蝶形运算单元所使用加法器和乘法器数量进行比较,其中算法一为传统快速算法,算法二为行排列的方法^[17] ...

2013

0.0

... 144 150帧视频信号为例,不同m、不同维度时本文算法与普通DCT处理视频信号耗时^[18]的实验比较 ...