作者简介:王庆年(1952-),男,教授,博士生导师.研究方向:节能与新能源汽车.E-mail:wqn@jlu.edu.cn
在既定的动力总成功率参数及整车控制策略前提下,为充分挖掘插电式混合动力汽车(PHEV)节能潜力,以满足整车性能为约束条件,以百公里行驶成本为响应,利用最优拉丁超立方设计方法探索了其传动系统所有因子的空间响应特性,辨别了系统关键设计因子,给出了最优局部区域。基于此,建立了系统径向基(RBF)神经网络模型,并充分利用非线性二次规划算法较强的局部优化能力,在上述局部区域内得到了传动系参数全局最优组合以及对应的百公里行驶成本。结果显示:基于近似模型的优化方法精度较高,误差为1.06%;百公里行驶成本降低了9.72%。
In order to fully explore the energy saving potential of plug-in hybrid electric vehicle with determined power parameters of powertrain and control strategy, and in meeting the vehicle performance constraints, the running cost of 100 km was proposed as the response. The optimal Latin hypercube design was used to investigate the spatial response characteristics of all factors of the transmission system, based on which the key design factors of the system were identified and the optimal local area was confirmed. Combined with making full use of the advantages of strong local optimization ability of nonlinear quadratic programming algorithm, the Radial Basis (RBF) neural network model was established to obtain global optimal solution and the best response of the optimization problem. The model error is 1.06% which shows that the optimization method based on approximation model is of high accuracy. The running cost of 100 km is reduced by 9.72%.
目前, 针对插电式混合动力汽车(Plug-in hybrid electric vehicle, PHEV)[1, 2]的研究多集中在开发较先进的优化算法, 例如利用动态规划算法、模糊逻辑控制算法、模型预测控制算法等对动力系统能量管理策略进行优化[3]; 利用遗传算法、自适应模拟退火算法等全局探索方法对动力传动系统参数自动离线寻优等[4]。上述研究方法仍存在一些问题:并没有考虑动力传动系统设计参数与目标函数之间的空间响应特性, 缺少对其准确的把握, 使之对工程实际应用的参考价值得不到充分的体现; 常见优化算法中目标函数确定方法是将车辆的动力性指标、经济性指标进行加权转化为单目标优化问题或者直接利用多目标优化算法进行优化[5], 其优化效率较低且评价指标具有一定的人为主观性。
本文以实际项目中某PHEV为研究对象, 以百公里行驶成本作为优化目标[6, 7], 利用最优拉丁超立方设计方法(Optimal Latin hypercube design, OptLHD)对优化参数响应空间特性进行探索, 从全局把握了最优设计区域。建立了传动系参数与百公里行驶成本之间的径向基神经网络(RBF nueral network)近似模型。最后充分利用非线性二次规划算法(NLPQL)较强的局部优化能力在最优设计区域对近似模型寻优, 得到了最优参数设计组合。通过以上研究, 既把握了因子与响应之间的空间特性, 又提高了优化效率。
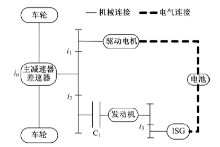
某插电式混合动力汽车结构如图1所示, 其中,
整车控制策略基于以下原则:首先, 将该PHEV工作过程分为电量消耗(Charge depleting, CD)和电量保持(Charge sustaining, CS)两个工作阶段; 其次, 结合该插电式混合动力汽车构型特点, 采用低速纯电动驱动、高速发动机优先参与工作的控制逻辑。具体控制思想如下:
(1)当车速
(2)当车速
(3)当车速
(4)当车速
(5)当车速
(6)当车速
(7)当制动踏板踩下且
其中,
(1)发动机以及电机模型
在已知发动机和电机准确的实验数据前提下, 通常将发动机和电机简化为参数插值查表模型以获得其输出特性, 并结合其自身特性对模型进行修正。在一定的发动机转速
式中:
(2)电池模型
若已知电池在一定温度
式中:
式中:
(3)整车动力学模型
根据PHEV的构型, 结合汽车方程可知:汽车行驶阻力转矩Treq 应等于动力总成驱动转矩Tt, 分别表示为:
式中:
(1)优化目标确定及参数选择
PHEV运行时分为电量消耗和电量维持两个阶段, 其燃油经济性应充分考虑以上两个阶段。传统评价方法主要有两种:一种是分别给出两个阶段的燃油经济性, 该种方法并不能直观体现PHEV总的燃油经济性; 另一种是等效燃油消耗量方法, 但等效转化建立在一定的估算效率基础上, 而效率容易受各种环境因素的影响, 故该种方法亦不能准确地反映出整车燃油经济性。提出以百公里行驶成本为评价指标, 将油耗、电耗统一转化为总消耗费用:
式中:
基于PHEV构型, 选择
(2)约束条件确定
整车最大总转矩需要满足最大爬坡度需求:
式中:
最高车速要求传动系匹配需满足以下条件:
式中:
由以上分析可知,
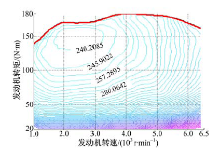
图2和图3为已选定发动机的万有特性图和ISG电机效率特性图。由图2~图3可以看出, 发动机和ISG电机高效率区间对应的转速区间大致分别为1300~3500 r/min和6000~13 000 r/min。综合考虑两者最优工作转速区间以及转矩特性, 并结合式(9)~(11)得到各传动比取值范围为:
(3)整车参数以及整车性能要求
整备质量m=1600 kg; 空气阻力系数CD=0.35; 迎风面积A=2.1 m2; 车轮滚动阻力系数
试验设计方法(Design of experiments, DOE)是数理统计学的一个分支。因其能够辨别系统关键设计因子、分析因子与响应之间的关系和趋势, 在工程和科研中应用非常广泛[8]。
最优拉丁超立方设计(Optimal Latin hypercube design, OptLHD)可以使所有的试验点尽量均匀的分布在设计空间, 具有非常好的空间填充性和均衡性[8]。具体做法是在
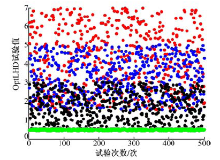
为了更全面地把握参数设计空间特性, 在试验设计中设置跨度较大的变量上、下限, 选择较大的抽样空间。在Matlab中编写最优拉丁超立方设计算法, 设定抽样空间为500, 生成样本初始空间。样本点分布情况如图4所示。
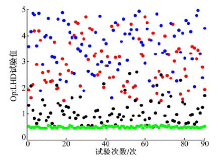
将以上初始样本点限制在约束范围之内, 得到最终样本点分布如图5所示, 共有90组样本点满足条件。图4和图5中红色代表
由图5可以看出, 最优拉丁超立方设计矩阵能够均匀地覆盖整个设计空间。以90组样本点为自变量输入整车模型, 结合整车控制策略在NEDC工况下进行仿真分析。设计过程中响应变化曲线如图6所示。
通过对以上所有满足条件的试验设计点进行试验研究, 可以初步得到上述设计参数组最优响应值为
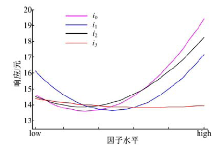
为进一步确定传动比优化空间, 需要了解因子的主效应, 其绘制方法如下:当某因子从较低水平增加到最大水平时, 用每个水平和其他因子的所有可能组合得到的响应的平均值分别作为横坐标和纵坐标可以得到该因子的主效应图。利用此方法得到所有因子主效应图, 如图7所示。
由图7可以看出因子
为进一步寻优得到全局最佳参数组合, 需要缩小可优化空间。缩小因子优化空间的原则是:在该空间内, 响应值应保持在较低的水平之内。在这里以主效应响应不超过最优样本点响应值
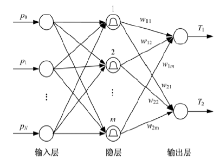
为进一步优化得到该PHEV动力系统的最佳传动比设计组合, 需先建立各传动比与百公里行驶成本之间的数学模型。插电式混合动力汽车的动力系统集电器、机械、化学和电控技术于一体, 是一种多输入多输出的高度非线性系统。各系统之间存在耦合关系, 难以严格按照解析法要求建立理论模型。近似模型能够起到减少仿真程序调用的时间、提高优化效率的作用, 有利于更快地收敛到全局最优点[8]。径向基神经网络模型较其他近似模型有较强的非线性逼近能力, 无需数学假设, 对函数的逼近能力是最优的, 可以以任意精度逼近任意连续函数[9, 10]。RBF网络模型如图8所示。
RBF网络中除输入输出层之外仅有一个隐层, 该层中的转换函数一般为是局部响应的高斯函数, 隐层中的神经元越多, 逼近越精确[11]。
RBF网络输入为:
在本问题中, 输出层只有一个输出。故RBF网络输出层节点函数为:
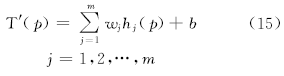
式中:
网络输出
式中:
本文采用Matlab编程, 以
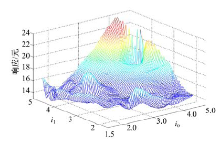
从误差变化曲线可以看出, 最终拟合均方误差为1.5× 10-24, 与目标均方误差0非常接近, 说明该神经网络模型精度非常高, 可以作为传动系参数优化模型。图10为RBF网络模型部分三维特性图。
图10表示RBF网络模型中传动系参数
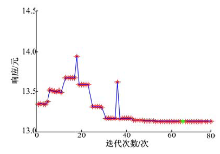
数值优化算法能够利用梯度、导数等数学特性非常高效地解决优化问题, 但是非常依赖初始设计点, 如果初始点选择不当会造成最终解落入局部解[8]。参考前文提供的非常准确的全局较优区域和可优化初始点, 利用数值优化方法中的非线性二次规划算法(NLPQL), 在Matlab中编程实现了基于RBF网络模型的优化方法。迭代过程如图11所示。
从数值优化结果可以看出最优传动比组合为:
将以上最优传动系参数组合作为原整车动力学模型的输入, 计算得到百公里行驶成本为12.9874元, 与RBF网络预测结果有1.06%的误差, 在允许范围之内。故通过基于RBF网络预测模型的数值优化方法得到的最优传动系参数组合, 可以节约成本。
将以上最优速比工程化得到最终传动比组合为
本文围绕某插电式混合动力汽车传动系参数匹配优化环节, 为避免人为主观评价因素, 提出以百公里行驶成本为系统响应。通过最优拉丁超立方设计探索了因子的空间响应特性、辨别了系统关键设计因子, 并定位了全局最优区域。为提高优化效率, 建立了误差较小的系统径向基神经网络近似模型。基于此, 利用局部优化能力较强的非线性二次规划算法在已定位的全局最优参数设计区域寻优, 得到了全局最优传动系参数组合。结果显示:除发动机与ISG电机之间的传动比
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|