先导阀前腔串加阻尼孔的新型双级溢流阀特性

引用本文

訚耀保, 原佳阳, 傅俊勇. 先导阀前腔串加阻尼孔的新型双级溢流阀特性. 2017, 47(1): 129-136
YIN Yao-bao, YUAN Jia-yang, FU Jun-yong. Characteristics of two-stage relief valve with series damping orifice in the front chamber of pilot valve. Journal of Jilin University Engineering and Technology Edition, 2017, 47(1): 129-136 复制到剪切板

Permissions

先导阀前腔串加阻尼孔的新型双级溢流阀特性

訚耀保¹, 原佳阳¹, 傅俊勇²

1.同济大学机械与能源工程学院,上海 200092

2.上海航天控制技术研究所,上海 201109

作者简介:訚耀保(1965-),男,教授,博士生导师.研究方向:极限环境下的液压与气动基础理论,飞行器能源与舵机,高速气动控制.E-mail:y-yin@tongji.edu.cn

基金:国家自然科学基金项目(51175378,51275356); 航空科学基金项目(20120738001,20128038003).

摘要

针对普通集成式双级溢流阀在空间尺寸限制时不能稳定溢流的问题,建立了普通集成式双级溢流阀框图,得到了先导阀稳定性判据。该判据表明集成式双级溢流阀主阀尺寸与先导阀存在匹配关系:过大的先导阀芯或过小的主阀尺寸将导致先导阀失稳,造成双级溢流阀无法稳定工作。提出了在先导阀前腔串加阻尼孔来实现极端小尺寸下先导阀与主阀稳定控制的新型集成式双级溢流阀方案,该串联阻尼孔避免了先导输入流量对先导阀芯运动的直接影响,通过阻尼作用降低了先导阀回路的开环增益。理论和试验结果表明:该新型溢流阀在极限小尺寸下可以稳定溢流,能提供更好的压力流量特性。

关键词: 仪器仪表技术; 液压; 极端小尺寸; 集成式双级溢流阀; 稳定性; 阻尼孔

中图分类号:TH137.52 文献标志码:A 文章编号:1671-5497(2017)01-0129-08

Characteristics of two-stage relief valve with series damping orifice in the front chamber of pilot valve

YIN Yao-bao¹, YUAN Jia-yang¹, FU Jun-yong²

1.School of Mechanical Engineering, Tongji University, Shanghai 200092, China

2.Shanghai Aerospace Control Technology Institute, Shanghai 201109, China

Abstract

The ordinary integral two-stage relief valve can not work steadily when its dimension is limited. To solve this problem, a mathematical model of two-stage relief valve is established and the stability criterion of the pilot valve is obtained. The criterion indicates that there is a matching relationship between the main valve size and the pilot valve size in integral two-stage relief valve. If the main valve size is too large or the pilot valve size is too small, the pilot valve will become unstable. A new type two-stage relief valve with a series damping orifice in the front chamber of pilot valve is proposed to achieve stable control of the pilot valve and main valve without increasing the volume of the relief valve. This damping orifice can avoid direct impact on the pilot valve core from the pilot input flow, and decrease the open loop gain of the pilot valve loop. Theoretical and experimental results show that the new type two-stage relief valve can work steadily and has a better pressure-flow characteristic with the extreme small size.

Keyword: technology of instrument and meter; hydraulics; extreme small size; integral two-stage relief valve; stability; damping orifice

Show Figures

0 引言

溢流阀是液压系统中调节压力的关键元件, 用于控制系统的工作压力^[1]。与单级溢流阀相比, 采用差动式压力控制原理的双级溢流阀控制流量大, 压力流量特性好, 已广泛应用于高压大流量的液压回路。国内外学者深入研究了溢流阀阀芯结构^{[2, 3, 4, 5]}、液阻和液容的优化设计^[6]。美国Merrit^[7]采用阻尼节流器和液容来改善单级溢流阀的性能。英国Watton^[8]系统地研究了双级溢流阀参数对阀特性的影响。在稳定性方面, 日本Hayashi^{[9, 10]}提出了双级溢流阀及其液压回路稳定性的分析方法; Hö s等^[11]研究了溢流阀中的分叉和振动等非线性现象。此外, 国内学者通过改变液阻分布, 采用π 桥溢流阀来降低双级溢流阀的稳态调压偏差^[1]; 文献[12]研究了双溢流阀在振动环境下的数学模型和特性。

随着高速重载液压伺服系统的发展需要, 液压元件的小型化、轻量化、集成化已成为一个重要的基础课题; 特别是飞机、火箭等飞行器对液压伺服系统的质量和体积提出了非常苛刻的要求^{[1, 13]}。双级溢流阀作为压力控制回路的重要元件, 要求能够在有限的空间内实现大流量时的压力精确控制, 常与其他液压元件一起采取集成式设计方式^{[14, 15]}。然而, 随着空间尺寸的减小, 特别是当双级溢流阀主阀或先导阀的一方达到极限小尺寸时, 主阀与先导阀的特性是否匹配、不匹配时经常出现在工作过程中的持续振荡和啸叫, 导致伺服系统无法完成必须的服役性能, 甚至产生故障或失效。目前, 空间尺寸存在限制情况下双级溢流阀主阀与先导阀的匹配关系尚不明确, 国内外关于双级溢流阀结构尺寸与稳定性分析较为少见。

为此, 本文研究了双级溢流阀先导阀与主阀的匹配关系, 分析了集成式双级溢流阀在极端小尺寸时的稳定性判据。提出一种在先导阀前腔串加阻尼小孔的极端小尺寸新型集成式双级溢流阀, 分析了该阀的基本特性。

1 双级溢流阀主阀与先导阀匹配关系

某飞行器液压伺服系统由于空间尺寸的限制, 伺服机构采用集成式双级溢流阀, 其额定压力为25 MPa、额定流量为90 L/min, 先导阀采用目前能加工的最小尺寸, 即通径为3 mm、质量为1 g的锥阀。在液压系统试验中发现, 该集成式双级溢流阀容易引起振动, 并伴随刺耳的噪声, 压力波动范围大, 启动特性差。为此, 本文首先分析双级溢流阀主阀尺寸与先导阀之间的匹配关系以及极端小尺寸下先导阀和主阀的稳定性判据。

1.1 双级溢流阀数学模型

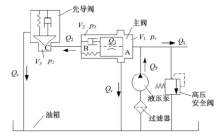
图1为普通双级溢流阀原理图。工作过程中, 液压泵油液流入主阀前腔(A腔), 容积为V₁, 通过主阀芯上的阻尼小孔进入主阀弹簧腔(B腔), 容积为V₂, 然后经由主阀与先导阀间流道流入先导阀入口容腔(C腔), 容积为V₃。由于油液压缩性导致先导锥阀入口容腔压力p₃增大, 当足以克服先导阀弹簧预压力时, 先导阀开启并产生溢流量Q_c。此时, 主阀前腔与弹簧腔之间的阻尼小孔节流作用而产生压差p_s-p₂, p_s为双级溢流阀控制压力, 当该压差足以克服主阀弹簧预压力时, 主阀开启并产生主溢流量 $\begin{matrix} Q_{v} 。 \end{matrix}$ 图1中容腔B和容腔C之间没有液阻, 因此两腔中油液压力总是相同的(即p₂=p₃), 共同构成了一个整体容腔, 即先导阀前腔, 其容积V=V₂+V₃; 采用集成式先导阀时, 结构上V₂≫V₃。

	Figure Option View Download New Window
	图1 普通双级溢流阀原理图Fig.1 Simplified model of ordinary two-stage relief valve

双级溢流阀的工作过程可分为先导阀开启前, 先导阀开启后到主阀开启前以及正常工作(主阀开启后)3个重要阶段。

(1)先导阀开启前的数学模型

先导阀开启之前, 先导阀和主阀处于关闭状态, 液压泵供给的油液通过阀内各容腔的假象充液, 与容腔内的压缩性流量相等。此时, 先导阀芯的力平衡方程为:

$\begin{matrix} p_{3} A_{c} + F_{c} - k_{c} x_{c 0} = 0 \end{matrix}$ (1)

式中:A_c 为先导阀口面积; k_c 为先导阀弹簧刚度; x_c0 为先导阀弹簧预压缩量; F_c为先导阀芯与阀座的作用力。

此时主阀没有开启, 主阀前腔和先导阀腔的流量连续性方程为:

$\begin{matrix} Q_{P} - Q_{L} = \frac{V_{1} + V_{2} + V_{3}}{E} \frac{d p_{s}}{dt} \end{matrix}$ (2)

式中:E为油液体积弹性模量; p_s=p₂=p₃ 。

(2)先导阀开启、主阀关闭时的数学模型

随着油液流入先导阀入口容腔, 先导阀芯与阀座之间的作用力F_c 随先导阀入口容腔压力p₃ 的增大而减小。当先导阀入口容腔压力p₃ 等于先导阀开启压力p_c0 (p_c0=k_c x_c0/A_c)时, F_c=0, 此后先导阀将开启溢流。阀芯开启后, 先导阀芯的力平衡方程为:

$p_{3} A_{c} = m_{c} \frac{d^{2} x_{c}}{d t^{2}} + (B_{c} + B_{cn}) \frac{d x_{c}}{dt} + k_{c} (x_{c} + x_{c 0}) + k_{cn} x_{c 0}$ (3)

$B_{cn} = ρl C_{d} π D_{c} \sin α_{c} \cdot \sqrt[]{2 p_{3} / ρ}$ (4)

$k_{cn} = C_{d} C_{v} π D_{c} p_{3} \sin 2 α_{c}$ (5)

式中:x_c 为先导阀芯开度; B_c 为先导阀阻尼系数; B_cn 为先导阀瞬态液动力阻尼; ρ 为油液密度; D_c 为先导阀口直径; α _c 为先导阀芯半角; C_d 为流量系数; C_v 为速度系数; k_cn 为先导阀稳态液动力刚度; m_c为先导阀芯的质量。

先导阀口处流量方程为:

$\begin{matrix} Q_{c} = C_{3} π D_{c} \sin α_{c} x_{c} \sqrt[]{\frac{2 p_{3}}{ρ}} \end{matrix}$ (6)

先导阀入口容腔与主阀弹簧腔之间没有压力损失, 是一个整体容腔(先导阀前腔), 其中的流量连续性方程为:

$\begin{matrix} Q_{1} - Q_{c} - A_{c} \frac{d x_{c}}{dt} = \frac{V_{2} + V_{3}}{E} \frac{d p_{2}}{dt} \end{matrix}$ (7)

假设主阀芯阻尼孔为薄壁小孔, 其流量方程为:

$\begin{matrix} Q_{1} = C_{2} \frac{π}{4} D_{1}^{2} \sqrt[]{\frac{2 (p_{s} - p_{2})}{ρ}} \end{matrix}$ (8)

式中: $\begin{matrix} C_{2} \end{matrix}$ 为主阀芯节流孔流量系数; $\begin{matrix} C_{3} \end{matrix}$ 为先导阀口流量系数; $\begin{matrix} D_{1} \end{matrix}$ 为主阀芯节流孔直径。

当先导阀溢流, 且主阀芯节流孔两侧油液压差不足以克服主阀弹簧预压力, 主阀尚未开启, 主阀芯的力平衡方程为:

$\begin{matrix} (p_{s} - p_{2}) A_{v} + F_{v} - k_{v} x_{v 0} = 0 \end{matrix}$ (9)

式中:A_v 为主阀阀口面积; F_v 为主阀阀芯与阀座的作用力; k_v 为主阀弹簧刚度; x_v0为主阀弹簧预压缩量。

主阀前腔流量连续性方程为:

$\begin{matrix} Q_{P} - Q_{L} - Q_{1} = \frac{V_{1}}{E} \frac{d p_{s}}{dt} \end{matrix}$ (10)

(3)先导阀开启、且主阀开启后的数学模型

主阀芯节流孔流量Q₁ 随先导阀溢流量Q_c 的增大而增大, 此时主阀前后的压差p_s-p₂ 增大, 主阀阀芯和阀座之间的机械压紧力F_v 逐渐减小。当F_v=0, 即主阀前后压差p_s-p₂ 等于主阀开启压差p_v0 (p_v0=k_v x_v0/A_v)时, 主阀开启, 双级溢流阀正常工作。主阀开启后, 主阀芯的力平衡方程为:

$(p_{s} - p_{2}) A_{v} = m_{v} \frac{d^{2} x_{v}}{d t^{2}} + (B_{v} + B_{vn}) \frac{d x_{v}}{dt} + k_{v} (x_{v} + x_{v 0}) + k_{vn} x_{v 0}$ (11)

$B_{vn} = ρl C_{d} π D_{v} \sin α_{v} \cdot \sqrt[]{2 p_{s} / ρ}$ (12)

$k_{vn} = C_{d} C_{v} π D_{v} p_{s} \sin 2 α_{v}$ (13)

式中:x_v 为主阀芯开度; B_v 为主阀阻尼系数; B_vn 为主阀瞬态液动力阻尼; k_vn 为主阀稳态液动力刚度; m_v为主阀芯的质量。

主阀前腔流量连续性方程为:

$\begin{matrix} Q_{P} - Q_{L} - Q_{v} - Q_{1} - A_{v} \frac{d x_{v}}{dt} = \frac{V_{1}}{E} \frac{d p_{s}}{dt} \end{matrix}$ (14)

主阀口节流方程为:

$\begin{matrix} Q_{v} = C_{1} π D_{v} \sin α_{v} x_{v} \sqrt[]{\frac{2 p_{s}}{ρ}} \end{matrix}$ (15)

式中:C₁ 为主阀口流量系数; α _v 为主阀芯半角; D_v为主阀阀口直径。

先导阀前腔的流量连续性方程为:

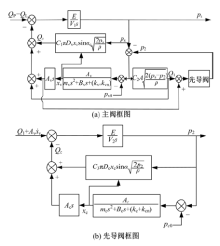
$\begin{matrix} Q_{1} - Q_{c} - A_{c} \frac{d x_{c}}{dt} + A_{v} \frac{d x_{v}}{dt} = \frac{V_{2} + V_{3}}{E} \frac{d p_{2}}{dt} \end{matrix}$ (16)

1.2 主阀和先导阀尺寸对先导阀稳定性的影响

当主阀和先导阀均开启, 双级溢流阀正常工作时, 由式(3)~(6)、式(8)和式(11)~(16)可得到双级溢流阀传递函数框图, 如图2所示。图2(a)中主阀输入为双级溢流阀入口流量Q_P-Q_L, 输出为双级溢流阀控制压力p_s; 图2(b)中先导阀输入为先导阀入口流量, 输出为先导阀控制压力 $\begin{matrix} p_{2} 。 \end{matrix}$

	Figure Option View Download New Window
	图2 双级溢流阀框图Fig.2 Block diagram of two-stage relief valve

由式(5), 先导阀口流量的线性化方程为:

$\frac{d Q_{c}}{dt} = k_{q} \frac{d x_{c}}{dt} + k_{c} \frac{d p_{3}}{dt}$ (17)

$k_{q} = \frac{\partial Q_{c}}{\partial x_{c x_{c} = x_{cx}, p_{3} = p_{cx}}} = C_{3} π D_{c} \sin α_{c} \sqrt[]{\frac{2 p_{cx}}{ρ}}$

$k_{c} = \frac{\partial Q_{c}}{\partial p_{3 x_{c} = x_{cx}, p_{3} = p_{cx}}} = C_{3} π D_{c} \sin α_{c} x_{cx} \sqrt[]{\frac{1}{2 ρ p_{cx}}}$

式中:k_q 为先导阀口流量增益; k_c 为先导阀口流量压力增益; x_cx 为先导阀芯开度; p_cx为先导阀前腔压力。

另外, 式(16)中 $\begin{matrix} A_{c} d x_{c} / dt \end{matrix}$ 表示先导阀芯运动对应的流量, 该项相对其他流量项较小, 可忽略不计。由于 $\begin{matrix} V_{2} ≫ V_{3}, 令 V = V_{2} + V_{3} \approx V_{2} 。 \end{matrix}$

根据式(17)可得在某开启位置线性化后先导阀框图, 如图3所示。

	Figure Option View Download New Window
	图3 在某开启位置线性化后先导阀框图Fig.3 Block diagram of linearization pilot valve at given open position

以先导阀输入流量 $\begin{matrix} Q_{1} + A_{v} {\overset{\cdot}{x}}_{v} \end{matrix}$ 为输入, 先导阀控制压力p₂ (或 p₃)为输出, 可得到先导阀闭环传递函数为:

$\begin{matrix} G (s) = \frac{b_{0} s^{2} + b_{1} s + b_{2}}{a_{0} s^{3} + a_{1} s^{2} + a_{2} s + a_{3}} \end{matrix}$ (18)

式中: $\begin{matrix} \begin{matrix} a_{0} = m_{c} V_{2}; a_{1} = B_{c} V_{2}; a_{2} = (k_{c} + k_{cn}) V_{2}; \\ a_{3} = A_{c} E C_{3} π D_{c} \sin α_{c} \sqrt[]{\frac{2}{ρ}} (1.5 \sqrt[]{p_{cx}} - \frac{p_{c 0}}{2 \sqrt[]{p_{cx}}}) \end{matrix} \end{matrix}$ ;

$\begin{matrix} b_{0} = m_{c} E; b_{1} = B_{c} E; b_{2} = (k_{c} + k_{cn}) E 。 \end{matrix}$

根据劳斯(Routh)稳定判据, 上述系统稳定的充要条件为 $\begin{matrix} a_{1} a_{2} > a_{0} a_{3}, \end{matrix}$ 代入相应参数可得:

$\begin{matrix} \begin{matrix} k_{c} + k_{cn} > k_{\min} = \\ \frac{m_{c} A_{c} E C_{3} π D_{c} \sin α_{c} \sqrt[]{\frac{2}{ρ}} (1.5 \sqrt[]{p_{cx}} - \frac{p_{c 0}}{2 \sqrt[]{p_{cx}}})}{B_{c} V_{2}} \end{matrix} \end{matrix}$ (19)

先导阀的静态压力超调率为:

$δ_{p} = \frac{p_{cT} - p_{c 0}}{p_{cT}}$ (20)

$p_{cT} = p_{c 0} + \frac{4 (k_{c} + k_{cn}) x_{cT}}{π D_{c}^{2}}$ (21)

式中:p_cT 为先导阀额定压力; x_cT为先导阀额定压力对应先导阀开度; 先导阀额定流量Q_cT为:

$\begin{matrix} Q_{cT} = C_{3} π D_{c} \sin α_{c} x_{cT} \sqrt[]{\frac{2 p_{cT}}{ρ}} \end{matrix}$ (22)

根据式(20)~(22), 可得锥阀开启压力 $\begin{matrix} p_{c 0} \end{matrix}$ 计算公式为:

$\begin{matrix} p_{c 0} = (1 - δ_{p}) {(\frac{4 (k_{c} + k_{cn}) Q_{cT}}{C_{3} π^{2} D_{c}^{3} \sin α_{c} δ_{p}} \sqrt[]{\frac{ρ}{2}})}^{\frac{2}{3}} \end{matrix}$ (23)

将式(19)的稳定性判据代入式(23), 可得先导阀在某一工作点 $\begin{matrix} (p_{cx}, x_{cx}) \end{matrix}$ 附近的稳定性判据为:

$\begin{matrix} p_{c 0} > p_{c 0 \min} (n) = C (n) \frac{Q_{cT} m_{c}}{V_{2}} \end{matrix}$ (24)

式中:C(n)为匹配系数, 表明各结构参数间的匹配关系; $\begin{matrix} C (n) = (1.5 \sqrt[]{n} - \frac{1 - δ_{p}}{2 \sqrt[]{n}}) \frac{(1 - δ_{p}) E}{δ_{p} B_{c}} \end{matrix}$ ; n表示先导阀工作点, n=p_cx/p_cT 。

为了保证先导阀工作过程中始终稳定, 式(24)应在任何工作点成立。匹配系数C(n)表达式中, 先导阀工作点n的最大值n_max表示先导阀控制压力p_c 的动态超调率σ _M, 则匹配系数C(n)的最大值为:

$\begin{matrix} \begin{matrix} C_{\max} = C (n_{\max}) = \\ (1.5 \sqrt[]{σ_{M}} - \frac{1 - δ_{p}}{2 \sqrt[]{σ_{M}}}) \frac{(1 - δ_{p}) E}{δ_{p} B_{c}} \end{matrix} \end{matrix}$ (25)

由此, 可以得到先导阀在任意工作点保持稳定的条件为:

$\begin{matrix} p_{c 0} - p_{c 0 \min} = p_{c 0} - C_{\max} \frac{Q_{cT} m_{c}}{V_{2}} > 0 \end{matrix}$ (26)

式(26)表明, 当先导阀额定流量和开启压力确定时, 先导阀的稳定性由主阀弹簧腔容积V₂ 和先导阀芯质量m_c 决定; 过大的先导阀芯质量或过小的主阀弹簧腔容积将导致先导阀失稳, 造成先导阀控制压力p₂ 的大范围持续波动。图2(a)中, 先导阀控制压力p₂ 通过主阀芯力平衡方程控制主阀芯位移x_v, 进而影响主阀溢流量Q_v 和主阀入口压力p_s; 因此, 先导阀控制压力p₂的失稳, 将造成主阀芯持续振荡和主阀控制压力的不稳定。

可见, 主阀尺寸和先导阀存在匹配关系, 即对于某一特定开启压力和额定流量的先导阀, 主阀弹簧腔容积V₂ 和先导阀芯质量m_c之间必须满足式(26)所示的匹配关系, 才能保证先导阀和主阀的稳定工作。

1.3 空间尺寸限制时双级溢流阀存在的问题

当空间结构尺寸有限时, 双级溢流阀的主阀和先导阀往往做成集成式结构, 甚至采用极端小尺寸结构, 但主阀弹簧腔容积 $\begin{matrix} V_{2} \end{matrix}$ 及先导阀芯质量m_c需要满足式(26)的稳定条件。某集成式双级溢流阀先导级设计要求如下:开启压力p_c0为16.5 MPa; 静态压力超调率δ _p< 10%; 动态压力超调率σ _M< 1.5; 额定溢流量Q_cT为4.1 L/min。根据现有加工条件, 其先导阀的最小可加工尺寸为通径D_c=3 mm, 质量m_c=1 g; 根据式(26), 主阀弹簧腔容积 $\begin{matrix} V_{2} \end{matrix}$ 应大于7.85 mL才能保证先导阀稳定工作。但由于空间尺寸限制, 该集成式双级溢流阀主阀弹簧腔容积 $\begin{matrix} V_{2} \end{matrix}$ 仅约为1.94 mL, 根据式(26)可知该先导阀不稳定, 双级溢流阀无法正常工作。

2 极端小尺寸新型双级溢流阀

2.1 先导阀前腔串加阻尼孔的双级溢流阀

式(26)表明, 普通双级溢流阀主阀弹簧腔容积V₂ 过小易造成先导阀控制压力p₃ 对先导阀前腔净流量(流入流量与流出流量之差)的变化更为敏感; 造成先导阀框图(见图3)中开环增益过大, 导致先导控制压力p₃的响应较快且超调较大。为了稳定先导阀动态特性, 减小先导阀开环增益, 这里提出一种先导阀前腔串加阻尼孔的双级溢流阀, 如图4所示, 与图1的普通双级溢流阀相比, 在原先导阀入口容腔和主阀弹簧腔之间串加了一个阻尼小孔。

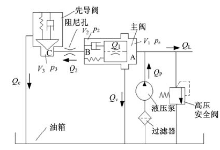	Figure Option View Download New Window
	图4 先导阀前腔串加阻尼孔的双级溢流阀原理图Fig.4 Simplified model of two-stage relief valve with a series damping orifice in pilot valve front chamber

对于前腔串加阻尼小孔的先导阀, 主阀弹簧腔B流量连续性方程为:

$\begin{matrix} Q_{1} - Q_{2} + A_{v} \frac{d x_{v}}{dt} = \frac{V_{2}}{E} \frac{d p_{2}}{dt} \end{matrix}$ (27)

先导阀入口容腔C流量连续性方程为:

$\begin{matrix} Q_{2} - Q_{c} - A_{c} \frac{d x_{c}}{dt} = \frac{V_{3}}{E} \frac{d p_{3}}{dt} \end{matrix}$ (28)

先导阀前腔串联的阻尼孔为细长孔, 其节流方程为:

$\begin{matrix} Q_{2} = \frac{π d^{4}}{128 μl} (p_{2} - p_{3}) \end{matrix}$ (29)

式中:d为阻尼小孔直径; l为细长孔孔深。

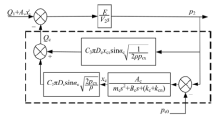
根据式(23)~(26)及式(27)~(29)可得前腔串加阻尼孔先导阀框图, 如图5所示。

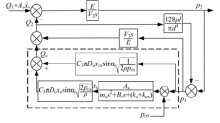	Figure Option View Download New Window
	图5 前腔串加阻尼孔先导阀框图Fig.5 Block diagram of pilot valve with a series damping orifice in pilot valve front chamber

化简可得如图6所示的简化后前腔串加阻尼孔先导阀框图。

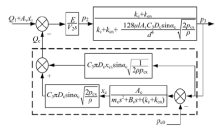	Figure Option View Download New Window
	图6 简化后前腔串加阻尼孔先导阀框图Fig.6 Simplified block diagram of pilot valve with a series damping orifice in pilot valve front chamber

对比图6和图3可知, 由于前腔加入串联阻尼孔, 避免了先导输入流量 $\begin{matrix} Q_{1} \end{matrix}$ 直接影响先导阀控制压力 $\begin{matrix} p_{3}; \end{matrix}$ 在先导阀框图前向环节串联了一个增益小于1的比例环节; 降低了先导阀回路的开环增益; 有利于先导控制压力 $\begin{matrix} p_{3} \end{matrix}$ 的稳定。

2.2 普通双级溢流阀与新型双级溢流阀动态特性

某集成式双级溢流阀相关参数如表1所示。

表1 某集成式双级溢流阀相关参数 Table 1 Parameters of an integral two-stage relief valve

使用Matlab, 通过四阶Runge-Kutta算法对式(1)~(16)求解可得改进前普通集成式双级溢流阀仿真结果; 对式(1)~(15)和式(27)~(29)求解可得改进后新型集成式双级溢流阀仿真结果, 新型集成式双级溢流阀在其先导阀前腔串加一个直径d=1.4 mm, 孔深l=8 mm的细长孔。

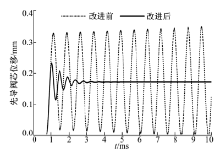
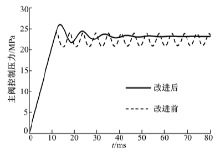
图7为串加阻尼孔前后先导阀芯位移动态特性。图7中, 串联阻尼孔前, 由于主阀与先导阀不匹配, 因而先导阀回路开环增益较大, 造成先导阀芯持续振荡; 而前腔串加阻尼孔后, 由于阻尼作用降低了先导阀回路开环增益, 先导阀芯运动趋于稳定。

	Figure Option View Download New Window
	图7 串加阻尼孔前后先导阀芯位移动态特性Fig.7 Dynamic characteristic of pilot valve core displacement

图8为串加阻尼孔前后双级溢流阀入口压力动态特性, 双级溢流阀入口流量为90 L/min。由于先导阀无法稳定工作, 先导控制压力p₂的波动导致主阀入口压力的持续波动, 因此改进前的双级溢流阀无法正常溢流。而新型集成式双级溢流阀的控制压力趋于稳定。

	Figure Option View Download New Window
	图8 串加阻尼孔前后双级溢流阀入口压力动态特性Fig.8 Dynamic characteristic of main valve inlet pressure

综上所述, 集成式双级溢流阀先导级的前腔采用带串联阻尼小孔结构, 理论上通过阻尼作用降低了先导阀回路的开环增益, 可以改善先导级动态特性, 增强先导阀稳定性; 很好地解决了空间尺寸限制时, 集成式溢流阀中先导阀稳定性差的问题。

3 试验结果及其分析

试验对象为普通集成式双级溢流阀和同样名义通径、先导阀前腔串加阻尼孔后的新型集成式双级溢流阀。其中, 普通集成式双级溢流阀的先导阀口直径D_c=3 mm, 先导阀前腔容积为1.94 mL; 而新型双级溢流阀在先导阀前腔串联加工了一个直径d=1.4 mm, 孔深l=8 mm的细长孔, 该阻尼孔将先导阀前腔分为容积为1.91 mL(主阀弹簧腔)和0.04 mL(先导阀入口腔容腔)的两个容腔。两个被测溢流阀的开启压力均为21 MPa, 额定溢流量均为90 L/min。

试验在某箭载伺服机构样机试验台上进行, 工作介质为8284航天煤油; 在试验台的液压泵出口和油箱之间安装被试溢流阀, 通过电脑测试系统测量上述两溢流阀的压力流量特性, 并将验台置于单独的封闭房间, 在距离液压试验台1 m处采用手持式噪声仪检测溢流阀工作时的试验台工作噪声。

试验结果表明:采用普通集成式双级溢流阀时, 试验台工作噪音为90 dB; 而采取新型集成式双级溢流阀时, 试验台工作噪声减少至62 dB。新型集成式双级溢流阀的工作噪声减小, 说明双级溢流阀的阀芯振荡得到了抑制, 主阀入口的压力流量较为稳定。

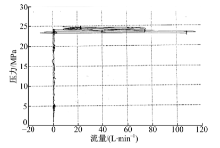
图9为普通集成式双级溢流阀压力流量特性试验结果。图9中, 双级溢流阀开启后出现压力流量波动, 特别是溢流量的波动幅度非常大, 不能稳定工作。根据上文分析可知波动是由于先导阀失稳, 先导控制压力不稳定, 造成主阀芯持续振荡。因此主阀控制压力在开启压力以上持续波动; 而溢流量则主要受到主阀芯开口量的影响而出现大范围变化。

	Figure Option View Download New Window
	图9 某普通集成式双级溢流阀压力流量特性试验结果Fig.9 Pressure-flow characteristics of ordinary two-stage relief valve

图10为同样名义通径的新型集成式双级溢流阀压力流量特性试验结果。可见, 改进后的新型集成式双级溢流阀具有更稳定的压力流量特性。

	Figure Option View Download New Window
	图10 新型集成式双级溢流阀压力流量特性试验结果Fig.10 Pressure-flow characteristics of new type two-stage relief valve

	Figure Option View Download New Window
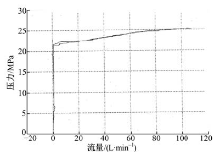
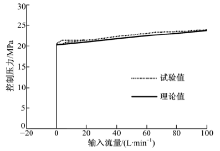	图11 集成式新型双级溢流阀流量压力特性理论结果与试验结果对比Fig.11 Theoretic and experiment pressure-outflow characteristic curves of new type two-stage relief valve

图11为改进后集成式新型双级溢流阀流量压力特性理论结果与试验结果对比图。根据上述数学模型得到的压力流量特性理论结果与双级溢流阀实验结果基本一致, 验证了本文数学模型的正确性。

4 结论

(1)普通集成式双级溢流阀主阀尺寸与先导阀存在匹配关系:过大的先导阀芯尺寸或过小的主阀尺寸会造成先导阀失稳。空间尺寸限制时, 由于主阀和先导阀之间容腔体积有限, 导致先导阀不稳定, 双级溢流阀无法正常工作。主阀和先导阀尺寸可通过本文得到的稳定性判据进行判定和设计。

(2)提出了一种极端小尺寸的集成式新型双级溢流阀方案, 该阀采用在先导阀前腔中串加了一个阻尼孔的新结构。理论和试验结果表明:先导阀前腔串加阻尼孔的新型双级溢流阀在不增加溢流阀尺寸的前提下, 通过阻尼作用降低了先导阀回路的开环增益, 解决了极端小尺寸时集成式溢流阀先导级稳定控制问题。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	訚耀保. 极端环境下的电液伺服控制理论及应用技术[M]. 上海: 上海科学技术出版社, 2012. [本文引用:3]
[2]	Park S H. Design and performance characteristic analysis of servo valve-type water hydraulic poppet valve[J]. Journal of Mechanical Science and Technology, 2009, 23(9): 2468-2478. [本文引用:1]
[3]	Lung F K K. A one dimensional quasi-steady model for prediction of safety valve lift characteristics[C]//Proceedings of the 2nd International Conference on Developments in Valves and Actuators for Fluid Control, Berlin, 1988: 83-101. [本文引用:1]
[4]	Dasgupta K, Karmakar R. Modeling and dynamics of single-stage pressure relief valve with directional damping[J]. Simulation Modeling Practice and Theory, 2002, 10(1): 51-67. [本文引用:1]
[5]	Opdenbosch P, Sadegh N, Book W J. Modeling and control of an electro-hydraulic poppet valve[C]//ASME International Mechanical Engineering Congress and Exposition, American Society of Mechanical Engineers, New York, 2004: 103-110. [本文引用:1]
[6]	路甬祥, 胡大纮, 郁凯元. 新原理比例溢流阀基型阀的开发[J]. 浙江大学学报: 自然科学版, 1985, 19(1): 32-43. Lu Yung-hsiang, Hu Da-hong, Yu Kai-yuan. The development of an advanced prototype relief valve on new principles[J]. Journal of Zhejiang University, 1985, 19(1): 32-43. [本文引用:1]
[7]	Merrit H E. Hydraulic Control Systems[M]. New York: John Willy & Sons, 1967. [本文引用:1]
[8]	Watton J. The stability and response of a two-stage pressure rate controllable relief valve[J]. Journal of Fluid Control, 1990, 20(3): 50-66. [本文引用:1]
[9]	Hayashi S. Instability of poppet valve circuit[J]. JSME International Journalon, Dynamics, Control, Robotics, Design and Manufacturing, 1995, 38(3): 357-366. [本文引用:1]
[10]	Hayashi S. Stability and nonlinear behavior of poppet valve circuits[C]//Proc 5th Triennial Int Symp on Fluid Control, Measurement and Visualization, Hayama, Japan, 1997: 13-20. [本文引用:1]
[11]	Hös C, Champneys A R. Grazing bifurcations and chatter in a pressure relief valve model[J]. Physica D: Nonlinear Phenomena, 2012, 241(22): 2068-2076. [本文引用:1]
[12]	刘洪宇, 张晓琪, 訚耀保. 振动环境下双级溢流阀的建模与分析[J]. 北京理工大学学报, 2015, 35(1): 13-18. Liu Hong-yu, Zhang Xiao-qi, Yin Yao-bao. Analysis of a two-stage relief valve under vibration environment[J]. Transactions of Beijing Institute of Technology, 2015, 35(1): 13-18. [本文引用:1]
[13]	Yang X, Paik M J, Pfaff J L. Pilot operated control valve having a poppet with integral pressure compensating mechanism[P]. U. S. Patent: 6745992, 2004-06-08. [本文引用:1]
[14]	Muller M T, Fales R C. Design and analysis of a two-stage poppet valve for flow control[J]. International Journal of Fluid Power, 2008, 9(1): 17-26. [本文引用:1]
[15]	Eyres R D, Champneys A R, Lieven N A J. Modelling and dynamic response of a damper with relief valve[J]. Nonlinear Dynamics, 2005, 40(2): 119-147. [本文引用:1]

2012

0.0

... 0 引言溢流阀是液压系统中调节压力的关键元件,用于控制系统的工作压力^[1] ...

... 桥溢流阀来降低双级溢流阀的稳态调压偏差^[1] ...

... 特别是飞机、火箭等飞行器对液压伺服系统的质量和体积提出了非常苛刻的要求^[1,13] ...

2009

0.0

... 国内外学者深入研究了溢流阀阀芯结构^[2,3,4,5]、液阻和液容的优化设计^[6] ...

1988

0.0

... 国内外学者深入研究了溢流阀阀芯结构^[2,3,4,5]、液阻和液容的优化设计^[6] ...

2002

0.0

... 国内外学者深入研究了溢流阀阀芯结构^[2,3,4,5]、液阻和液容的优化设计^[6] ...

2004

0.0

... 国内外学者深入研究了溢流阀阀芯结构^[2,3,4,5]、液阻和液容的优化设计^[6] ...

1985

0.0

. 1985, 19(1):32-43

The development of an advanced prototype relief valve on new principles

新原理比例溢流阀基型阀的开发

Lu Yung-hsiang , Hu Da-hong , Yu Kai-yuan.

路甬祥, 胡大纮, 郁凯元

本文介绍的一种新原理比例溢流阀基型阀,改进了美国人Havvy Vickers在1936年发明并沿用至今的差压式溢流阀的开环控制原理,应用了1980年春提出并登记专利的系统压力直接检测,反馈的原理,使阀的主要稳态性能有数倍的提高;同时采用了级间动压反馈的原理,显著提高了阀的动态稳定性。文中用传递函数的方法说明基型阀与传统型式阀控制原理的区别。介绍了阀的试验研究和动态仿真的结果。该阀的开发具有广泛的应用前景,可发展出一个流体压力控制器件的新家族。

... 国内外学者深入研究了溢流阀阀芯结构^[2,3,4,5]、液阻和液容的优化设计^[6] ...

1967

0.0

... 美国Merrit^[7]采用阻尼节流器和液容来改善单级溢流阀的性能 ...

1990

0.0

... 英国Watton^[8]系统地研究了双级溢流阀参数对阀特性的影响 ...

1995

0.0

... 在稳定性方面,日本Hayashi^[9,10]提出了双级溢流阀及其液压回路稳定性的分析方法 ...

1997

0.0

... 在稳定性方面,日本Hayashi^[9,10]提出了双级溢流阀及其液压回路稳定性的分析方法 ...

2012

0.0

... s等^[11]研究了溢流阀中的分叉和振动等非线性现象 ...

2015

0.0

. 2015, 35(1):13-18 DOI:doi:10.15918/j.tbit1001-0645.2015.01.003

Analysis of a two-stage relief valve under vibration environment

振动环境下双级溢流阀的建模与分析

Liu Hong-yu , Zhang Xiao-qi , Yin Yao-bao.

刘洪宇, 张晓琪, 訚耀保

The relief valves used in aircrafts must keep functioning properly under initial rising time and vibration conditions. It is the focus to find an effective method for analyzing the performance of the relief valves and to build up the mathematical models under vibration condition. The results show that relief valve with balance piston has the function of anti-vibration, noise elimination and constant pressure, and the two-stage relief valve works in three important stages: the precursor relief valve opening stage, the main relief valve opening stage and normal working conditions. Vibration condition has great influence on the pressure characteristics of two-stage relief valve and the structure parameters decide the delay time and dynamic characteristics. The theoretical results are consistent well with the experimental results. The mathematical models of relief valve under vibration are useful for the production and development of new valve.

为研究溢流阀在液压能源启动过程、整机振动环境下保持必要的服役性能,建立了振动环境下双级溢流阀的数学模型及特性的分析方法. 研究结果表明:溢流阀先导阀作成平衡活塞防振尾端结构形式可以实现减振、消声、稳压的功能;双级溢流阀分为先导阀开启前、主阀开启前和稳定工作3个阶段;整机振动对双级溢流阀压力控制性能的影响大;结构参数决定了溢流阀的延迟时间和动态特性.

2004

0.0

... 特别是飞机、火箭等飞行器对液压伺服系统的质量和体积提出了非常苛刻的要求^[1,13] ...

2008

0.0

... 双级溢流阀作为压力控制回路的重要元件,要求能够在有限的空间内实现大流量时的压力精确控制,常与其他液压元件一起采取集成式设计方式^[14,15] ...

2005

0.0