串并混联机床几何误差建模与实验

引用本文

曲兴田, 赵永兵, 刘海忠, 王昕, 杨旭, 陈行德. 串并混联机床几何误差建模与实验. 2017, 47(1): 137-144
QU Xing-tian, ZHAO Yong-bing, LIU Hai-zhong, WANG Xin, YANG Xu, CHEN Hang-de. Modeling and experiment of spatial geometric errors of hybrid serial-parallel machine tool. Journal of Jilin University Engineering and Technology Edition, 2017, 47(1): 137-144 复制到剪切板

Permissions

串并混联机床几何误差建模与实验

曲兴田, 赵永兵, 刘海忠, 王昕, 杨旭, 陈行德

吉林大学机械科学与工程学院,长春 130022

作者简介:曲兴田(1962-),男,教授.研究方向:智能精密制造.E-mail:quxt@jlu.edu.cn

基金:国家自然科学基金项目(51135006).

摘要

以多体系统理论为基础,研究了串并混联机床的几何误差。考虑各运动轴的定位误差、直线度误差、角度误差以及垂直度误差的综合作用,提出一种机床综合误差建模方法。通过对该机床各部件拓扑结构进行抽象化描述,推导出混联机床两相邻体间相对运动的特征矩阵,建立了混联机床的整机综合误差模型。利用激光干涉仪对X、Y轴多项几何误差进行测量,并将测得的几何误差带入综合误差模型。通过分析所测的各项几何误差以及综合误差分布和演变规律发现:X、Y轴定位误差对整机综合误差的影响最大,直线度误差次之,角度误差影响最小;在精度要求不高的情况下,角度误差对综合误差的影响可忽略。

关键词: 机械制造自动化; 综合误差模型; 几何误差; 串并混联机床

中图分类号:TH161 文献标志码:A 文章编号:1671-5497(2017)01-0137-08

Modeling and experiment of spatial geometric errors of hybrid serial-parallel machine tool

QU Xing-tian, ZHAO Yong-bing, LIU Hai-zhong, WANG Xin, YANG Xu, CHEN Hang-de

College of Mechanical Science and Engineering, Jilin University, Changchun 130022, China

Abstract

The spatial geometric error of hybrid serial-parallel machine tool is modeled and investigated. This synthesis error model is based on multi-body system and the consideration of the combined effect of positioning errors, straightness errors, squareness errors and angular errors of each axis. With substantial data measured by laser interferometer, the distribution maps of some errors are drawn. By choosing a planned curve on the surface of workpiece and moving each axis with errors, the spatial geometric error appears and is illustrated on Matlab. Further, by decomposing the spatial geometric errors along each axis of spatial coordinate and comparing with position errors of the corresponding axis, a conclusion is drawn that both errors have close value and the same distribution trend. The positioning errors have the greatest impact on the synthesis error, followed by the straightness errors. The impact of the angular errors on the synthesis error can be ignored.

Keyword: mechanical manufacturing automation; synthesis error model; geometric error; hybrid serial-parallel machine tool

Show Figures

0 引言

机床的精度主要受准静态几何误差、控制系统误差、热变形误差、切削负载误差、机床的振动误差、环境干扰误差等的影响, 其中机床准静态几何误差约占整机误差的70%左右^[1]。

几何误差的建模方法有很多, 其中应用最广的有D-H变换矩阵法和刚体运动学法^[2]。此外还有误差矩阵法、矢量微分法、二次型法、神经网络法、变分法等。韩飞飞等^[3]以多体系统理论为基础对三轴数控机床进行了几何误差建模和分析。朱建忠等^[4]应用变分法建立了机床几何误差模型。Wahid等^[2]应用刚体运动学和齐次变换法对五轴磨床几何误差进行建模。Chen等^[5]应用齐次变换矩阵建立了五轴机床的空间误差模型, 并对模型的37项误差进行了敏感性分析。Cui等^[6]基于多体系统理论建立了机床几何误差模型, 并对3种常见的运动制定了补偿算法。Chen等^[7]基于微分变换理论提出了一种几何误差建模方法, 用矩阵的形式把各误差元作为微分算子, 并通过计算雅克比矩阵来进行建模和补偿。Fu等^[8]根据机床运动的几何特性建立了一种指数型(POE)几何误差模型, 并在三轴立式加工中心进行实验验证。王维等^[9]综合研究了机床几何误差和热误差, 根据几何误差和热误差的不同特性分离出几何误差。

串联机床几何误差建模方法较多, 而并联机构几何误差建模的方法较少。孟婥等^[10]依据全微分理论提出了Stewart型并联六坐标测量机原始误差和执行机构末端位姿误差模型。程刚等^[11]基于矩阵全微分理论建立了以3-RPS并联机构为核心的机械腿的位姿误差模型。Fan等^[12]建立了3-PRS并联机床几何误差模型, 并对该机床的几何误差模型进行了敏感度分析。黄田等^[13]利用空间矢量链分析方法, 构造出三平动自由度并联机构的末端位置和姿态与几何误差之间的映射关系。李新友等^[14]利用正交设计对3-RPS并联机构进行了精度分析和精度综合, 将执行末端的位姿误差的极差值作为敏感系数, 得到了给定精度下21项几何原始误差的公差。Sun等^[15]利用雅克比矩阵及敏感度分析成功分离出3自由度并联机器人可补偿和不可补偿的几何误差, 但并未给出各误差的变化规律以及误差之间的关系。

几何误差测量的方法一般分为间接测量和直接测量。间接测量是一种通过测量机床加工工件的误差来衡量机床精度的方法, 一般用在机床的误差溯源上。比较典型的间接测量包括Weikert等^[16]提出的R-test法, Hong等^[17]提出的非接触式R-test法, 平面正交光栅法以及双球规(DBB)法等。其中Hong等^[17]利用非接触式R-test法对机床位置误差进行了测量评定, Lee等^[18]用双球规测量了五轴机床旋转轴的位置误差。还有一些通过误差辨识来间接测量几何误差的方法, 常用的有22线法^[19]、15线法^[20]、对角线矢量法^[21]等。直接测量是通过测量仪器直接测量机床各轴的几何误差的方法, 一般可以直接测得机床的各项误差值, 常用的测量仪器有激光干涉仪、激光跟踪仪、六自由度激光测量系统等^[22]。韩飞飞等^[3]利用激光干涉仪测量了三轴数控机床各运动单元的定位误差、直线度误差、偏摆角误差和俯仰角误差。Zhong等^[23]分别用激光干涉仪和激光跟踪器测得大型五轴加工中心的移动轴和转动轴误差。

本文以多体系统理论为基础, 建立了混联叶片磨抛机床的几何误差模型, 用激光干涉仪对机床的部分几何误差进行了测量并借助Matlab进行误差分析。

1 混联机床的多体系统理论

1.1 相邻体的位姿关系

根据多体系统理论, 在体 $\begin{matrix} B_{j} \end{matrix}$ 和 $\begin{matrix} B_{i} \end{matrix}$ 上分别建立与体固连的坐标系 $\begin{matrix} O_{j} - X_{j} Y_{j} Z_{j} \end{matrix}$ 和 $\begin{matrix} O_{i} - X_{i} Y_{i} Z_{i} 。 \end{matrix}$ 若坐标 $\begin{matrix} O_{i} - X_{i} Y_{i} Z_{i} \end{matrix}$ 系绕其X轴旋转α 、绕Y轴旋转β 、绕Z轴旋转γ , 沿X轴平移a, 沿Y轴平移b, 沿Z轴平移c后与O_j-X_jY_jZ_j重合, 则体 $\begin{matrix} B_{j} \end{matrix}$ 与 $\begin{matrix} B_{i} \end{matrix}$ 的姿态和位置关系可由齐次变换矩阵式(1)来表示:

$\begin{matrix} _{j}^{i} T_{p} = [\begin{matrix} cosβcosγ & sinαsinβcosγ - cosαsinγ & cosαsinβcosγ + sinαsinγ & a \\ cosβsinγ & sinαsinβsinγ + cosαcosγ & cosαsinβsinγ - sinαcosγ & b \\ - sinβ & sinαcosβ & cosαcosβ & c \\ 0 & 0 & 0 & 1 \end{matrix}] \end{matrix}$ (1)

其中, 式(1)中左上角3× 3矩阵表示 $\begin{matrix} B_{j} \end{matrix}$ 与 $\begin{matrix} B_{i} \end{matrix}$ 之间的姿态关系, 右上角1× 3矩阵表示 $\begin{matrix} B_{j} \end{matrix}$ 与 $\begin{matrix} B_{i} \end{matrix}$ 之间的位置关系。在 $\begin{matrix} α 、 β 、 γ \end{matrix}$ 足够小的情况下, $\begin{matrix} cosk~ 1, sink~k (k = α, β, γ) 。 \end{matrix}$ 忽略2阶以上无穷小, 则式(1)可简化为式(2):

$\begin{matrix} _{j}^{i} T_{p} = [\begin{matrix} 1 & - γ & β & a \\ γ & 1 & - α & b \\ - β & α & 1 & c \\ 0 & 0 & 0 & 1 \end{matrix}] \end{matrix}$ (2)

若点 $\begin{matrix} P_{j} = (X_{j}, Y_{j}, Z_{j} {, 1)}^{Τ} \in O_{j} - X_{j} Y_{j} Z_{j}, \end{matrix}$ 该点在 $\begin{matrix} O_{i} - X_{i} Y_{i} Z_{i} \end{matrix}$ 内可表示为式(3):

$\begin{matrix} P_{ji} = (X_{ji}, Y_{ji}, Z_{ji} {, 1)}^{Τ} =_{j}^{i} T_{p} P_{j} \end{matrix}$ (3)

1.2 混联机床及其拓扑结构

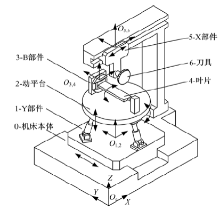
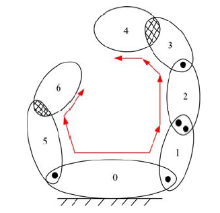
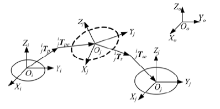
图1为混联叶片磨抛机床的结构示意图。图2为其拓扑结构。部件1和5由丝杠带动, 沿导轨滑移实现 $\begin{matrix} x 向和 y \end{matrix}$ 向运动。磨削工具头6装夹在部件5上。部件1和2通过3个电动缸并联实现Z轴平移、A轴转动,

	Figure Option View Download New Window
	图1 混联叶片磨抛机床机构示意图Fig.1 Serial-parallel machine tool

	Figure Option View Download New Window
	图2 机床拓扑结构Fig.2 Topological structure of machine tool

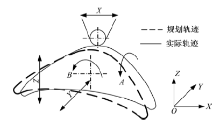
部件1和部件2的相对位置可通过并联机构的运动学正解和逆解进行确定。部件3绕 $\begin{matrix} B \end{matrix}$ 轴旋转带动叶片4做回转运动。在床身上指定空间坐标系(参考坐标系) $\begin{matrix} O_{o} - X_{o} Y_{o} Z_{o} \end{matrix}$ , 各运动部件上均建立与体固连的局部坐标系 $\begin{matrix} O_{k} - X_{k} Y_{k} Z_{k} (k = 1, 2, \dots, 6) 。 \end{matrix}$ 为了减少运算量, 部件1与部件2坐标系重合, 部件3与工件4坐标系重合, 部件5与刀具6坐标系重合, 且每个坐标系对应的X、Y、Z轴相互平行。

2 混联机床几何误差综合建模

在理想成型运动中, 刀具切削点与工件上规划的轨迹点应完全重合。由于各运动部件在不同方向上均存在几何误差, 导致刀具切削点偏离规划的轨迹点, 从而产生几何误差, 如图3所示。

	Figure Option View Download New Window
	图3 综合误差示意图Fig.3 Schematic diagram of spatial geometric error

2.1 几何误差识别

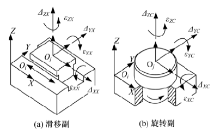
根据误差与运动参数之间的关系, 可将误差分为运动误差和位置误差。运动误差是与运动参数有关的变量。图4(a)为一滑移副, 当体 $\begin{matrix} B_{j} \end{matrix}$ 相对体 $\begin{matrix} B_{i} 沿 X \end{matrix}$ 轴滑移时会在6个自由度方向产生误差, 分别为:定位误差 $\begin{matrix} Δ_{XX} 、 \end{matrix}$ 直线度误差 $\begin{matrix} Δ_{YX} \end{matrix}$ 和 $\begin{matrix} Δ_{ZX} 、 \end{matrix}$ 滚转角误差 $\begin{matrix} ε_{XX} 、 \end{matrix}$ 俯仰角误差 $\begin{matrix} ε_{YX} 、 \end{matrix}$ 偏摆角误差 $\begin{matrix} ε_{ZX} 。 \end{matrix}$ 图4(b)为一旋转副, 当体 $\begin{matrix} B_{j} \end{matrix}$ 相对 $\begin{matrix} B_{i} 沿 Z \end{matrix}$ 轴旋转时会产生轴向误差 $\begin{matrix} Δ_{ZC} 、 \end{matrix}$ 径向误差 $\begin{matrix} Δ_{XC} \end{matrix}$ 和 $\begin{matrix} Δ_{YC} 、 \end{matrix}$ 定位误差 $\begin{matrix} ε_{ZC} 、 \end{matrix}$ 两倾斜角误差 $\begin{matrix} ε_{XC} \end{matrix}$ 和 $\begin{matrix} ε_{YC} 。 \end{matrix}$

	Figure Option View Download New Window
	图4 位置相关误差Fig.4 Position independent errors of prismatic joint and rotary joint

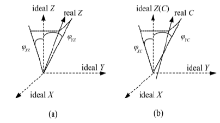
位置误差是与运动参数无关的常量。如图5(a)所示, 实际的Z轴与理想的X轴、Y轴不垂直, 垂直度误差分别为φ _XZ与φ _YZ 。同理, C轴与理想的Z轴不平行, 沿X轴和Y轴的平行度误差分别为 $\begin{matrix} φ_{XC} \end{matrix}$ 与 $\begin{matrix} φ_{YC}, \end{matrix}$ 如图5(b)所示。

	Figure Option View Download New Window
	图5 位置无关误差Fig.5 Position dependent errors

混联床能够实现X、Y、Z、A、B轴运动, 机床存在30(5× 6)个运动误差。设实际X轴与参考坐标系Y轴重合, 实际X轴和实际Y轴通过的平面为参考平面, Y轴相对X轴有一个垂直度误差φ _XV, Z轴相对X轴和Y轴有两个垂直度误差 $\begin{matrix} φ_{XZ} \end{matrix}$ 和 $\begin{matrix} φ_{XZ} \end{matrix}$ 。同理,A轴沿Y轴和Z轴有两个平行度误差 $\begin{matrix} φ_{YA} \end{matrix}$ 和φ _ZA, B轴沿X轴和Z轴有两个平行度误差 $\begin{matrix} φ_{XB} \end{matrix}$ 和 $\begin{matrix} φ_{ZB} \end{matrix}$ 。综上, 忽略工件及刀具装夹误差, 混联叶片磨抛机床共有37项几何误差。

2.2 相邻体间的实际运动过程

图6为体 $\begin{matrix} B_{j} \end{matrix}$ 相对 $\begin{matrix} B_{i} \end{matrix}$ 相对运动。 $\begin{matrix} B_{j} \end{matrix}$ 相对 $\begin{matrix} B_{i} \end{matrix}$ 的位置可由如下一系列齐次变换矩阵乘积来表示:

$\begin{matrix} _{j}^{i} T =_{j}^{i} T_{p} \cdot_{j}^{i} T_{pe} \cdot_{j}^{i} T_{s} \cdot_{j}^{i} T_{se} (4) \end{matrix}$

式中: $\begin{matrix} _{j}^{i} T_{p} \end{matrix}$ 为相对静止时理想的位置变换矩阵; 由于位置误差的存在, $\begin{matrix} _{j}^{i} T_{pe} \end{matrix}$ 为对应的位置误差变换矩阵; $\begin{matrix} _{j}^{i} T_{s} \end{matrix}$ 为相对运动时理想的变换矩阵; 由于误差的存在, $\begin{matrix} _{j}^{i} T_{se} \end{matrix}$ 为对应的运动误差变换矩阵。

	Figure Option View Download New Window
	图6 相邻体实际运动过程Fig.6 Movement of adjacent bodies with geometric errors

2.3 相邻体位姿变换矩阵

(1)0-1体之间有一个自由度, 沿 $\begin{matrix} y \end{matrix}$ 向, 所以有:

$_{1}^{0} T =_{1}^{0} T_{p} \cdot_{1}^{0} T_{pe} (Y) \cdot_{1}^{0} T_{s} (Y) \cdot_{1}^{0} T_{se} (Y)$ (5)

式中：

$_{1}^{0} T_{p} = [\begin{matrix} 1 & 0 & 0 & X_{01} \\ 0 & 1 & 0 & Y_{01} \\ 0 & 0 & 1 & Z_{01} \\ 0 & 0 & 0 & 1 \end{matrix}],$

$_{1}^{0} T_{pe} (Y) = [\begin{matrix} 1 & - φ_{XY} & 0 & 0 \\ φ_{XY} & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}],$

$_{1}^{0} T_{s} (Y) = [\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & Y \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}],$

$_{1}^{0} T_{se} (Y) = [\begin{matrix} 1 & ε_{ZY} & ε_{YY} & Δ_{XY} \\ ε_{ZY} & 1 & - ε_{XY} & Δ_{YY} \\ - ε_{YY} & ε_{XY} & 1 & Δ_{ZY} \\ 0 & 0 & 0 & 1 \end{matrix}] 。$

(2)1-2体之间有两个自由度, 分别沿Z向和A向, 故有:

$_{2}^{1} T =_{2}^{1} T_{p} \cdot_{2}^{1} T_{pe} (Z) \cdot_{2}^{1} T_{pe} (A) \cdot_{2}^{1} T_{s} (Z) \cdot_{2}^{1} T_{s} {(A)}_{2}^{1} T_{se}$ (6)

式中：

$_{2}^{1} T_{p} = I_{4 \times 4} (四阶单位矩阵),$

$_{2}^{1} T_{pe} (Z) = [\begin{matrix} 1 & - φ_{XZ} & 0 & 0 \\ φ_{XZ} & 1 & - φ_{YZ} & 0 \\ 0 & φ_{YZ} & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}],$

$_{2}^{1} T_{pe} (A) = [\begin{matrix} 1 & - φ_{YA} & φ_{ZA} & 0 \\ φ_{YA} & 1 & 0 & 0 \\ - φ_{ZA} & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}],$

$_{2}^{1} T_{s} (Z) = [\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & Z \\ 0 & 0 & 0 & 1 \end{matrix}],$

$_{2}^{1} T_{s} (A) = [\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & cosA & - sinA & 0 \\ 0 & sinA & cosA & 0 \\ 0 & 0 & 0 & 1 \end{matrix}],$

$_{2}^{1} T_{se} (Z) = [\begin{matrix} 1 & - ε_{ZZ} & ε_{YZ} & Δ_{XZ} \\ ε_{ZZ} & 1 & - ε_{XZ} & Δ_{YZ} \\ - ε_{YZ} & ε_{XZ} & 1 & Δ_{ZZ} \\ 0 & 0 & 0 & 1 \end{matrix}],$

$_{2}^{1} T_{se} (A) = [\begin{matrix} 1 & - ε_{ZA} & ε_{YA} & Δ_{XA} \\ ε_{ZA} & 1 & - ε_{XA} & Δ_{YA} \\ - ε_{YA} & ε_{XA} & 1 & Δ_{ZA} \\ 0 & 0 & 0 & 1 \end{matrix}] 。$

(3)2-3体之间有一个自由度, 沿 $\begin{matrix} B \end{matrix}$ 向, 故有:

$_{3}^{2} T =_{3}^{2} T_{p} \cdot_{3}^{2} T_{pe} (B) \cdot_{3}^{2} T_{s} (B) \cdot_{3}^{2} T_{se} (B)$ (7)

式中：

$_{3}^{2} T_{p} = [\begin{matrix} 1 & 0 & 0 & X_{23} \\ 0 & 1 & 0 & Y_{23} \\ 0 & 0 & 1 & Z_{23} \\ 0 & 0 & 0 & 1 \end{matrix}],$

$_{3}^{2} T_{pe} (B) = [\begin{matrix} 1 & - φ_{XB} & 0 & 0 \\ φ_{XB} & 1 & - φ_{ZB} & 0 \\ 0 & φ_{ZB} & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}],$

$_{3}^{2} T_{s} (B) = [\begin{matrix} cosB & 0 & sinB & 0 \\ 0 & 1 & 0 & 0 \\ - sinB & 0 & cosB & 0 \\ 0 & 0 & 0 & 1 \end{matrix}],$

$_{3}^{2} T_{se} (B) = [\begin{matrix} 1 & - ε_{ZB} & ε_{YB} & Δ_{XB} \\ ε_{ZB} & 1 & - ε_{XB} & Δ_{YB} \\ - ε_{YB} & ε_{XB} & 1 & Δ_{ZB} \\ 0 & 0 & 0 & 1 \end{matrix}] 。$

(4)3-4体之间, 忽略工件装夹误差, 所以有:

$\begin{matrix} _{4}^{3} T = I_{4 \times 4} \end{matrix}$ (8)

(5)0-5体之间有一个自由度, 沿 $\begin{matrix} X \end{matrix}$ 向, 所以有:

$_{5}^{0} T =_{5}^{0} T_{p} \cdot_{5}^{0} T_{pe} \cdot_{5}^{0} T_{s} \cdot_{5}^{0} T_{se}$ (9)

式中：

$_{5}^{0} T_{p} = [\begin{matrix} 1 & 0 & 0 & X_{05} \\ 0 & 1 & 0 & Y_{05} \\ 0 & 0 & 1 & Z_{05} \\ 0 & 0 & 0 & 1 \end{matrix}],$

$_{5}^{0} T_{s} = [\begin{matrix} 1 & 0 & 0 & X \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}],$

$_{5}^{0} T_{se} = [\begin{matrix} 1 & - ε_{ZX} & ε_{YX} & Δ_{XX} \\ ε_{ZX} & 1 & - ε_{XX} & Δ_{YX} \\ - ε_{YX} & ε_{XX} & 1 & Δ_{ZX} \\ 0 & 0 & 0 & 1 \end{matrix}] 。$

(6)5-6体之间, 忽略刀具装夹误差, 所以有:

$\begin{matrix} _{6}^{5} T = I_{4 \times 4} \end{matrix}$ (10)

2.4 几何误差综合建模

假设刀具磨削点坐标为: $\begin{matrix} P_{t} = (X_{t}, Y_{t}, Z_{t}, 1) 。 \end{matrix}$ 根据式(3), 经一系列坐标转化, 它在空间坐标系的坐标为:

$\begin{matrix} P_{t 0} = (X_{t 0}, Y_{t 0}, Z_{t 0} {, 1)}^{Τ} =_{5}^{0} T \cdot_{6}^{5} T \cdot P_{t} \end{matrix}$

假设规划的轨迹点坐标为: $\begin{matrix} P_{w} = (X_{w}, Y_{w}, Z_{w}, 1) 。 \end{matrix}$ 同理, 经坐标变换后, 它在空间坐标的系坐标为:

$\begin{matrix} \begin{matrix} P_{w 0} = \\ (X_{w 0}, Y_{w 0}, Z_{w 0} {, 1)}^{Τ} =_{1}^{0} T \cdot_{2}^{1} T \cdot_{3}^{2} T \cdot_{4}^{3} T \cdot P_{w} \end{matrix} \end{matrix}$

空间几何误差可表示为:

$E = (E_{X}, E_{Y}, E_{Z}, 0) Τ = P_{t 0} - P_{w 0} =_{5}^{0} T \cdot_{6}^{5} T \cdot P_{t} -_{1}^{0} T \cdot_{2}^{1} T \cdot_{3}^{2} T \cdot_{4}^{3} T \cdot P_{w}$ (11)

式中：

$\sqrt[]{E_{X}^{2} + E_{Y}^{2} + E_{Z}^{2}} = E_{d}$ (12)

3 混联机床几何误差测量及分析

3.1 混联机床几何误差测量

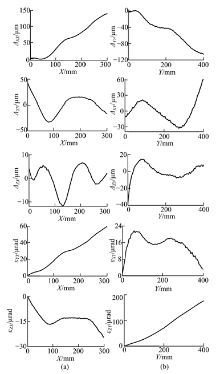
几何误差的测量是基于Renishaw^®公司的XL-80激光干涉仪完成的。由于客观条件限制, 测量项主要为:X轴和Y轴的定位误差、直线度误差、俯仰角误差和偏摆角误差。图7为X轴沿Y向直线度误差测量现场。根据多次测量, 得到图8所示各项误差分布图。

	Figure Option View Download New Window
	图7 直线度误差测量现场Fig.7 Measuring scene of straightness error of X axis

	Figure Option View Download New Window
	图8 混联机床X、Y轴几何误差分布图Fig.8 Distribution of geometric errors of X-axis and Y-axis

图8(a)为 $\begin{matrix} X \end{matrix}$ 轴几何误差分布情况。定位误差Δ _XX在0~300 mm呈近似线性分布, 在x=300 mm处达到最大, 为140.6 μ m。沿 $\begin{matrix} Y \end{matrix}$ 向定位误差Δ _YX在x=0处误差最大为43.92 μ m, 在0~145 mm误差变化幅度较大, 在145~300 mm误差变化较平缓。沿 $\begin{matrix} Z 向定位误差 Δ_{ZX} 与 Δ_{YX} \end{matrix}$ 相比数值较小, 波动较大, 在x=130 mm处达到最大, 为-11.96 μ m。 $\begin{matrix} X \end{matrix}$ 轴俯仰角误差ε _YX在0~300 mm内呈近似线性增长, 在x=300 mm处误差达到最大, 为59.54 μ rad。 $\begin{matrix} X 轴偏摆角误差 ε_{ZX} \end{matrix}$ 比俯仰角误差小, 在x=95~255 mm内误差略有波动, 其余位置波动较大, 在x=300 mm处达到最大, 为-24.79 μ rad。

图8(b)为 $\begin{matrix} Y \end{matrix}$ 轴几何误差分布情况。定位误差 $\begin{matrix} Δ_{YY} \end{matrix}$ 呈直线式波动上升, 并且在y=400 mm处达到最大, 为-106.14 μ m。沿 $\begin{matrix} X 向直线度误差 Δ_{XY} \end{matrix}$ 变化幅度较大, 在y=300~400 mm处增长率较高。在y=400 mm处达到最大, 为61.83 μ m。沿 $\begin{matrix} Z 向直线度误差 Δ_{ZY} \end{matrix}$ 在y=0处达到最大, 为-39.61 μ m, 在y=0~80 mm极速增长, 在y=80~400 mm处变化幅度较小。 $\begin{matrix} Y 轴俯仰误差 ε_{XY} \end{matrix}$ 在y=0~60 mm处由0增长到最大, 为21.78 μ rad。在60~400 mm处除短暂小幅攀升外, 呈下降趋势。 $\begin{matrix} Y 轴偏摆误差 ε_{ZY} \end{matrix}$ 在整个行程呈线性增长, 在y=400 mm处达到最大, 为175.78 μ rad。

3.2 几何误差综合分析

联动 $\begin{matrix} X 、 Y \end{matrix}$ 轴做直径为200 mm的圆形插补运动, 将测得的误差带入几何误差综合分析模型, 观察 $\begin{matrix} X 、 Y \end{matrix}$ 轴误差项对综合误差影响情况。从图9可以直观看出实际轨迹与计划轨迹的空间偏离情况, 将综合误差沿切削轨迹点展开可得综合误差沿各切削点分布情况, 如图10(a)所示, 误差区间为0.022~0.164 mm。

	Figure Option View Download New Window
	图9 综合误差空间分布Fig.9 Distribution of comprehensive error

	Figure Option View Download New Window
	图10 综合误差沿各切削点分布Fig.10 Distribution of comprehensive error along each cutting point

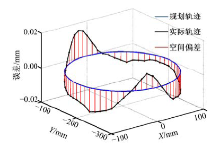
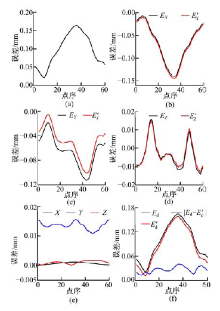
为了研究综合误差沿各轴向分布情况及影响因素, 将空间综合误差沿各轴向展开, 并与对应轴的定位误差、直线度误差进行比较。图10(c)和10(d)为各轴向几何误差E_i (i=X, Y, Z)与去除角度误差后的几何误差E'_i (i=X, Y, Z)的比较图, 可以看出:E_i 与E'_i (i=X, Y, Z)分布趋势相同, 数值上略有偏差, 偏差分布见图10(e)。从10(e)可以看出:X、Z轴偏差较小, 在0附近波动, Y轴偏差稍大, 在0.01~0.02 mm间波动, 主要是由于Y轴较大的偏摆角误差ε _ZY 引起。鉴于E_i 与E'_i(i=X, Y)有相近的分布趋势和误差方向, 可通过数值积分定量计算其接近程度。即将两条误差曲线各自积分后与综合误差相应分量相比, 面积比即可代表误差比。计算后得到X、Y方向去除角度误差后的几何误差E'_i 占其轴向几何误差E_i的比例分别为99.13%、82.05%。Z方向无定位误差, X、Y轴在Z方向的直线度误差占Z方向误差的92.81%。图10(f)为空间综合误差E_d与去除角度误差后的综合误差E'_d比较情况, 二者分布趋势相似, 数值偏差在0.01~0.04 mm间波动。去除角度误差后的综合误差E'_d占空间综合误差E_d的93.24%。由此可见, 角度误差对综合误差的影响很小。

为了进一步分析综合误差沿各轴向展开分量与对应轴的定位误差、直线度误差各自的关系, 用上述方法计算得:X轴的定位误差占到综合误差在X轴方向分量的84.13%; Y轴在X方向的直线度误差占综合误差在X轴方向分量的16.81%; Y轴的定位误差占到综合误差在Y轴方向分量的84.89%; X轴在Y方向的直线度误差占到综合误差在Y轴方向分量的5.75%。由此可见, 对综合误差影响程度最大是定位误差, 直线度误差次之, 角度误差最小。

4 结论

(1)以多体系统理论为基础, 充分考虑各轴定位误差、直线度误差和角度误差的综合作用, 建立了几何误差综合分析模型。

(2)利用Renishaw双频激光干涉仪对机床 $\begin{matrix} X 、 Y \end{matrix}$ 轴共10项几何误差进行测量, 根据多次测量的结果得出各项几何误差的分布情况。

(3)将测得几何误差带入几何误差综合分析模型, 分析 $\begin{matrix} X 、 Y \end{matrix}$ 轴几何误差对综合误差的影响。通过比较分析发现, 各轴几何误差主要受定位误差和直线度误差的影响, 受角度误差影响最小。

(4)通过数值积分计算, 定量计算出各误差元对综合误差的影响程度。对综合误差影响程度最大是定位误差, 占到80%以上, 直线度误差次之, 角度误差最小。在机床精度要求不高的情况下, 可以忽略角度误差对综合误差的影响。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Ramesh R, Mannan M A, Poo A N. Error compensation in machine tools—a review part I: geometric, cutting-force induced and fixture-dependent errors[J]. International Journal of Machine Tools & Manufacture, 2000, 40(9): 1235-1256. [本文引用:1]
[2]	Wahid Khan Abdul, Chen Wu-yi. Systematic geometric error modeling for workspace volumetric calibration of 5-axis turbine blade grinding machine[J]. Chinese Journal of Aeronautics, 2010, 23(5): 604-615. [本文引用:2]
[3]	韩飞飞, 赵继, 张雷, 等. 数控机床几何精度综合解析与试验研究[J]. 机械工程学报, 2012, 48(21): 141-147. Han Fei-fei, Zhao Ji, Zhang Lei, et al. Comprehensive analysis and experimental study on the geometric accuracy of CNC machine tools[J]. Journal of Mechanical Engineering, 2012, 48(21): 141-147. [本文引用:2]
[4]	朱建忠, 李圣怡, 黄凯. 超精密机床变分法精度分析及其应用[J]. 国防科技大学学报, 1997, 19(2): 36-40. Zhu Jian-zhong, Li Sheng-yi, Huang Kai. Variational method of ultra-precision machine tool accuracy analysis and its application[J]. Journal of National University of Defense Technology, 1997, 19(2): 36-40. [本文引用:1]
[5]	Chen G, Liang Y, Sun Y, et al. Volumetric error modeling and sensitivity analysis for designing a five-axis ultra-precision machine tool[J]. International Journal of Advanced Manufacturing Technology, 2013, 68(9-12): 2525-2534. [本文引用:1]
[6]	Cui G, Lu Y, Li J, et al. Geometric error compensation software system for CNC machine tools based on NC program reconstructing[J]. International Journal of Advanced Manufacturing Technology, 2012, 63(1-4): 169-180. [本文引用:1]
[7]	Chen J, Lin S, He B. Geometric error compensation for multi-axis CNC machines based on differential transformation[J]. International Journal of Advanced Manufacturing Technology, 2014, 71(1-4): 635-642. [本文引用:1]
[8]	Fu G, Fu J, Xu Y, et al. Product of exponential model for geometric errorintegration of multi-axis machine tools[J]. International Journal of Advanced Manufacturing Technology, 2014, 71(9-12): 1653-1667. [本文引用:1]
[9]	王维, 杨建国, 姚晓栋, 等. 数控机床几何误差和热误差综合建模及实时补偿[J]. 机械工程学报, 2012, 48(7): 165-170. Wang Wei, Yang Jian-guo, Yao Xiao-dong, et al. Comprehensive modeling and real-time compensation of geometric error and thermal error of CNC machine tools[J]. Journal of Mechanical Engineering, 2012, 48(7): 165-170. [本文引用:1]
[10]	孟婥, 车仁生. 并联六坐标测量机的误差模型和误差补偿[J]. 哈尔滨工业大学学报, 2004, 36(3): 317-320. Meng Chuo, Che Ren-sheng. Error model and error compensation of six-freedom-degree parallel mechanism CMM[J]. Journal of Harbin Institute of Technology, 2004, 36(3): 317-320. [本文引用:1]
[11]	程刚, 葛世荣. 3-RPS对称并联式机械腿误差模型及分析[J]. 中国矿业大学学报, 2009, 38(1): 50-55. Cheng Gang, Ge Shi-rong. Error model and analysis of 3-RPS symmetrical parallel robot leg with three degree-of-freedom[J]. Journal of China University of Mining & Technology, 2009, 38(1): 50-55. [本文引用:1]
[12]	Fan Kuang-chao, Wang Hai, Zhao Jun-wei, et al. Sensitivity analysis of the 3-PRS parallel kinematic spindle platform of a serial-parallel machine tool[J]. International Journal of Machine Tool & Manufacture, 2003, 43(15): 1561-1569. [本文引用:1]
[13]	黄田, 李亚, 李思维, 等. 一种三自由度并联机构几何误差建模、灵敏度分析及装配工艺设计[J]. 中国科学(E辑), 2002, 32(5): 628-635. Huang Tian, Li Ya, Li Si-wei, et al. Modeling, sensitivity analysis and assembly process design for a 3-DOF parallel mechanism[J]. Science in China(Series E), 2002, 32(5): 628-635. [本文引用:1]
[14]	李新友, 陈五一, 韩先国. 基于正交设计的 3-RPS 并联机构精度分析与综合[J]. 北京航空航天大学学报, 2011, 37(8): 979-984. Li Xin-you, Chen Wu-yi, Han Xian-guo. Accuracy analysis and synthesis of 3-RPS parallel machine based on orthogonal design[J]. Journal of Beijing University Aeronautics and Astronautics, 2011, 37(8): 979-984. [本文引用:1]
[15]	Sun Tao, Song Yi-min, Li Yong-gang. Separation of comprehensive geometrical errors of a 3-DOF parallel manipulator based on jacobian matrix and its sensitivity analysis with monte-carlo method[J]. Chinese Journal of Mechanical Engineering, 2011, 24(3): 406-413. [本文引用:1]
[16]	Weikert S. R-test, a new device for accuracy measurements on five axis machine tools[J]. CIRP Annals-Manufacturing Technology, 2013, 53(1): 429-432. [本文引用:1]
[17]	Hong C F, Ibaraki S. Non-contact R-test with laser displacement sensors for error calibration of five-axis machine tools[J]. Precision Engineering Journal of the International Societies For Precision Engineering and Nanotechnology, 2013, 37(1): 159-171. [本文引用:2]
[18]	Lee K I, Yang S H. Robust measurement method and uncertainty analysis for position-independent geometric errors of a rotary-axis using a double ball-bar[J]. International Journal of Precision Engineering and Manufacturing, 2013, 14(2): 231-239. [本文引用:1]
[19]	Zhang G, Ouyang R, Lu B, et al. A displacement method for machine geometry calibration[J]. CIRP Annals Manufacturing Technology, 1988, 37(1): 515-518. [本文引用:1]
[20]	Chen G, Yuan J, Ni J. A displacement measurement approach for machine geometric error assessment[J]. International Journal of Machine Tools & Manufacture, 2001, 41(1): 149-161. [本文引用:1]
[21]	Wang C. Laser vector measurement technique for the determination and compensation of volumetric positioning errors[J]. Basic Theory, Review of Scientific Instruments, 2000, 71(10): 3933-3937. [本文引用:1]
[22]	Cui C, Feng Q, Zhang B, et al. System for simultaneously measuring 6 DOF geometric motion errors using a polarization maintaining fiber-coupled dual-frequency laser[J]. Optics Express, 2016, 24(6): 6735-6748. [本文引用:1]
[23]	Zhong G, Wang C, Yang S, et al. Position geometric error modeling, identification and compensation for large 5-axis machining center prototype[J]. International Journal of Machine Tools & Manufacture, 2015, 89: 142-150. [本文引用:1]

2000

0.0

... 0 引言机床的精度主要受准静态几何误差、控制系统误差、热变形误差、切削负载误差、机床的振动误差、环境干扰误差等的影响,其中机床准静态几何误差约占整机误差的70%左右^[1] ...

2010

0.0

... 几何误差的建模方法有很多,其中应用最广的有D-H变换矩阵法和刚体运动学法^[2] ...

... Wahid等^[2]应用刚体运动学和齐次变换法对五轴磨床几何误差进行建模 ...

2012

0.0

... 韩飞飞等^[3]以多体系统理论为基础对三轴数控机床进行了几何误差建模和分析 ...

... 韩飞飞等^[3]利用激光干涉仪测量了三轴数控机床各运动单元的定位误差、直线度误差、偏摆角误差和俯仰角误差 ...

1997

0.0

... 朱建忠等^[4]应用变分法建立了机床几何误差模型 ...

2013

0.0

... Chen等^[5]应用齐次变换矩阵建立了五轴机床的空间误差模型,并对模型的37项误差进行了敏感性分析 ...

2012

0.0

... Cui等^[6]基于多体系统理论建立了机床几何误差模型,并对3种常见的运动制定了补偿算法 ...

2014

0.0

... Chen等^[7]基于微分变换理论提出了一种几何误差建模方法,用矩阵的形式把各误差元作为微分算子,并通过计算雅克比矩阵来进行建模和补偿 ...

2014

0.0

... Fu等^[8]根据机床运动的几何特性建立了一种指数型(POE)几何误差模型,并在三轴立式加工中心进行实验验证 ...

2012

0.0

... 王维等^[9]综合研究了机床几何误差和热误差,根据几何误差和热误差的不同特性分离出几何误差 ...

2004

0.0

... 孟婥等^[10]依据全微分理论提出了Stewart型并联六坐标测量机原始误差和执行机构末端位姿误差模型 ...

2009

0.0

... 程刚等^[11]基于矩阵全微分理论建立了以3-RPS并联机构为核心的机械腿的位姿误差模型 ...

2003

0.0

... Fan等^[12]建立了3-PRS并联机床几何误差模型,并对该机床的几何误差模型进行了敏感度分析 ...

2002

0.0

... 黄田等^[13]利用空间矢量链分析方法,构造出三平动自由度并联机构的末端位置和姿态与几何误差之间的映射关系 ...

2011

0.0

. 2011, 37(8):979-984

Accuracy analysis and synthesis of 3-RPS parallel machine based on orthogonal design

基于正交设计的 3-RPS 并联机构精度分析与综合

Li Xin-you , Chen Wu-yi , Han Xian-guo.

李新友, 陈五一, 韩先国

School of Mechanical Engineering and Automation, Beijing University of Aeronautics and Astronautics, Beijing 100191, China

To analyze the influence degree of pose parameters on pose errors, and to guarantee the accuracy requirements of 3-RPS parallel mechanism in the whole workspace, the orthogonal design method was adopted for accuracy analysis and accuracy synthesis. According to the orthogonal design method, three pose parameters of 3-RPS parallel mechanism were considered as three factors for pose errors, and the pose error values from range analysis were introduced as error sensitive indexes. The influence degree of pose parameters on pose errors were obtained through range analysis. The factors were divided into reasonable levels based on the ratio of error sensitive indexes, and then more reasonable poses from orthogonal table were provided for accuracy synthesis. Accuracy synthesis was carried out according to the orthogonal table and tolerance values of 21 geometry original errors were derived according to accuracy requirements. The result shows that: By applying the orthogonal design method in accuracy analysis and synthesis, the influence degree of pose parameters on pose errors was analyzed completely, the accuracy synthesis results ensure the accuracy requirements in the whole workspace and a reference was provided for the development of prototype.

为了分析3-RPS并联机构在整个工作空间内各个位姿参数对位姿误差的影响程度,并且使该机构在整个工作空间内都满足精度要求,利用正交设计的思想对该机构进行了精度分析与精度综合.根据正交设计的思想,把该机构的3个位姿参数看成对位姿误差有影响的3个因素,用位姿误差的极差值作为敏感系数,通过极差分析得到了位姿参数对位姿误差的影响程度.以敏感系数的比值为依据合理划分各个因素的水平数,使排列的正交表为精度综合提供更加合理的位姿,对表中的各个位姿进行精度综合,得到了给定精度要求下的21项几何原始误差的公差值.结果表明:用正交设计的思想可以分析清楚位姿参数对位姿误差的影响程度,精度综合结果使机构在整个工作空间内满足精度要求,为物理样机的研制提供了参考.

... 李新友等^[14]利用正交设计对3-RPS并联机构进行了精度分析和精度综合,将执行末端的位姿误差的极差值作为敏感系数,得到了给定精度下21项几何原始误差的公差 ...

2011

0.0

... Sun等^[15]利用雅克比矩阵及敏感度分析成功分离出3自由度并联机器人可补偿和不可补偿的几何误差,但并未给出各误差的变化规律以及误差之间的关系 ...

2013

0.0

... 比较典型的间接测量包括Weikert等^[16]提出的R-test法,Hong等^[17]提出的非接触式R-test法,平面正交光栅法以及双球规(DBB)法等 ...

2013

0.0

... 比较典型的间接测量包括Weikert等^[16]提出的R-test法,Hong等^[17]提出的非接触式R-test法,平面正交光栅法以及双球规(DBB)法等 ...

... 其中Hong等^[17]利用非接触式R-test法对机床位置误差进行了测量评定,Lee等^[18]用双球规测量了五轴机床旋转轴的位置误差 ...

2013

0.0

... 其中Hong等^[17]利用非接触式R-test法对机床位置误差进行了测量评定,Lee等^[18]用双球规测量了五轴机床旋转轴的位置误差 ...

1988

0.0

... 还有一些通过误差辨识来间接测量几何误差的方法,常用的有22线法^[19]、15线法^[20]、对角线矢量法^[21]等 ...

2001

0.0

... 还有一些通过误差辨识来间接测量几何误差的方法,常用的有22线法^[19]、15线法^[20]、对角线矢量法^[21]等 ...

2000

0.0

... 还有一些通过误差辨识来间接测量几何误差的方法,常用的有22线法^[19]、15线法^[20]、对角线矢量法^[21]等 ...

2016

0.0

... 直接测量是通过测量仪器直接测量机床各轴的几何误差的方法,一般可以直接测得机床的各项误差值,常用的测量仪器有激光干涉仪、激光跟踪仪、六自由度激光测量系统等^[22] ...

2015

0.0

... Zhong等^[23]分别用激光干涉仪和激光跟踪器测得大型五轴加工中心的移动轴和转动轴误差 ...