作者简介:张家旭(1985-),男,博士研究生.研究方向:汽车地面力分析与控制.E-mail:zhjx_686@163.com
提出一种基于粒子群优化(PSO)算法和修正的Gauss-Newton算法的混合优化方法,对纯纵滑和纯侧偏工况下UniTire轮胎模型的特征参数进行辨识。为充分发挥两个算法的优点,首先,利用粒子群优化算法的全局区域的搜索优势辨识出UniTire轮胎模型的特征参数近似解,然后,利用修正的Gauss-Newton算法局部搜索优势在近似解邻近区域获得UniTire轮胎模型的特征参数的最优解。最后,对辨识结果进行残差分析,结果表明:用辨识数据参数化的UniTire轮胎模型具有较高的精度,可满足构建车辆底盘电控系统硬件在环仿真测试环境的需求。
A hybrid optimization method is proposed based Particle Swarm Optimization (PSO) algorithm and modified Gauss-Newton (S-N) algorithm, which is used for characteristic parameter identification of UniTire model under pure longitudinal slip and pure cornering conditions. Taking the full advantages of the two algorithms, the approximate solutions are identified first using the PSO algorithm, which is superior in global search; then, the optimal solutions of the parameters are obtained in the neighboring region of the approximate solutions by using the modified G-N algorithm, which is superior in local search. The results of residual analysis of the identified parameters show that the parameterized UniTire model with the identified results has high accuracy, and can meet the requirements to establish hardware in the loop simulation test environment for electric control unit of the vehicle chassis.
轮胎与路面的接触是产生车辆运动的主要外力来源, 研究轮胎的受力状态对设计和分析先进车辆底盘控制系统、以及优化设计车辆系统结构至关重要[1]。为了研究轮胎的受力状态, 国内外学者提出了许多轮胎模型, 如FTire模型[2]、Gim模型[3]以及Magic Formula模型[4]等。UniTire轮胎模型是由郭孔辉院士[1]在理论分析和试验研究的基础上提出的半经验“ 指数公式” 轮胎力学模型, 可以精确描述轮胎在各种工况下的受力状态, 并考虑动摩擦特性的影响, 在应用于车辆动力学的研究之前需要采用轮胎纵滑、侧偏工况的试验数据对公式中涉及的特征参数进行辨识。
目前, 轮胎模型的特征参数辨识大部分采用数值优化算法和智能搜索算法。文献[5]采用Excel Systems工具内置的非线性动态规划算法求解引擎来辨识UniTire轮胎模型的特征参数。文献[6]采用遗传算法对Magic Formula模型中表征轮胎侧向力与侧偏角关系的特征参数进行辨识。文献[7]基于遗传算法对LuGre轮胎模型的静态特征参数和动态特征参数进行辨识。文献[8]基于新自适应差分进化算法辨识Magic Formula模型的特征参数。基于数值优化算法的轮胎模型的特征参数辨识可在局部区域内搜索到最优解, 但对特征参数的初值选择较多地依赖于工程经验, 如果工程经验不够丰富, 很难给出合理的初值。智能优化算法虽然具有较强的鲁棒性, 能够在全局范围内逼近最优解, 但局部搜索能力差, 且收敛速度慢[9]。
基于此, 本文先利用粒子群优化(PSO)算法的全局搜索能力获得UniTire轮胎模型特征参数的近似最优解, 将其作为修正的Gauss-Newton算法(G-N算法)的参数初始值, 从而解决基于数值优化算法的UniTire轮胎模型在特征参数辨识过程中初始值选择依赖工程经验的问题。同时, 再利用修正的G-N算法在局部区域内辨识出精确的特征参数, 从而解决粒子群优化算法在局部区域内搜索能力差、收敛速度慢的不足。文中对纯纵滑、纯侧偏工况下的UniTire轮胎模型的特征参数进行了辨识, 并对辨识结果进行残差分析。
UniTire轮胎模型用如下关系式描述轮胎在纯纵滑工况和纯侧偏工况下所受的无量纲作用力
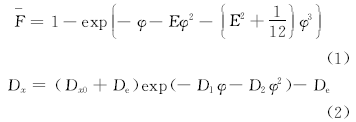
式中:
轮胎的纵向力
式中:
在UniTire轮胎模型中, 定义无量纲垂直载荷:
式中:
同时, 定义轮胎的纵向和侧向滑移率如下:
式中:
在纯纵滑工况下, UniTire轮胎模型中无量纲纵向力表示为[10]:
式中:
纵向刚度系数
纵向动态摩擦因数
式中:
因此, 纯纵滑工况下式(7)中特征参数向量为
在纯侧偏工况下, UniTire轮胎模型中无量纲侧向力表示为[10]:
式中:
侧偏刚度系数
侧向动态摩擦因数
式中:
因此, 纯侧偏工况下式(11)中特征参数向量为
近似最优解的辨识过程通过粒子群优化算法实现, 该算法以鸟类的捕食运动作为参考模型, 将每个优化问题的解定义为搜索空间中的一只鸟, 称为“ 粒子” 。每个粒子具有和鸟类捕食运动类似的行为规则, 从搜索空间中的随机解出发, 通过迭代运算寻找最优解。在每一次迭代中, 粒子根据当前所处的状态来调整自己的飞行速度, 即粒子本身所搜索到的最优解和整个种群目前找到的最优解来调整自己, 从而使整个粒子群的运动表现出与和鸟类捕食运动类似的特性用于求解复杂的优化问题。
对于UniTire轮胎模型的辨识问题, 假设特征参数向量解的个体在
式中:
研究发现[11]:较大的惯性权值使算法保持了较强的全局探测能力, 在迭代后期, 较小的惯性权值有利于进行更精确的局部寻优。因此, 本文采用文献[12]提出的惯性权值随时间线性减小的策略来改变惯性权重的取值, 其具体公式如下:
式中:
同时, 每个粒子的适应值用最优化问题的目标函数来评价。UniTire轮胎模型特征参数辨识问题可以转化为最小化残差
式中:
算法具体流程如下所示。
1.初始化粒子群中的每个粒子
2.While适应度最小误差标准或最大迭代数均未达到
3. For 每个粒子
4. 按式(18)计算惯性权重
5. 按式(16)更新粒子的速度
6. 按式(17)更新粒子的位置
7. 按式(19)计算粒子适应度
8. If 粒子当前适应度优于该粒子历史最优适应度
9. Then 用历史最优适应度值和位置更新当前适应度和位置
10. End
11. 选择当前粒子群中适应度最优的粒子
12. If 当前粒子群中最优适应度优于群内历史最优适应度
13. Then 用粒子群历史最优适应度和最优位置更新当前种群内最优适应度和最优粒子的位置
14.End
修正的G-N算法在参数初值选择适当条件下求解局部最优解, 具有收敛速度快、收敛精度高的优势[13]。本文将粒子群优化算法的辨识结果作为修正的G-N算法的初始值, 该算法的基本思想是将目标函数
经转换运算得到如下迭代公式:
为了避免Hessen矩阵
式中:采用几何级数法设置正则参数
考虑式(19)定义的最小残差, 且令
式中:
令
本文采用轮胎为某公司生产的225/55R17型号轮胎, 试验条件如下:
纯纵滑工况的纵向力试验数据:当垂直载荷
0, ± 0.0050, ± 0.0070, ± 0.0099, ± 0.0123, ± 0.0147, ± 0.0168, ± 0.0197,
± 0.0239, ± 0.0299, ± 0.0380, ± 0.0489, ± 0.0605, ± 0.0737, ± 0.1135,
± 0.1873, ± 0.2574, ± 0.3295, ± 0.4120, ± 0.4845, ± 0.5612, ± 0.6355,
± 0.7062, ± 0.7837, ± 0.8639, ± 0.9273。
0, ± 0.0019, ± 0.0028, ± 0.0042, ± 0.0043, ± 0.0053, ± 0.0061, ± 0.0069,
± 0.0083, ± 0.0083, ± 0.0098, ± 0.0105, ± 0.0134, ± 0.0151, ± 0.0173,
± 0.0181, ± 0.0193, ± 0.0220, ± 0.0247, ± 0.0292, ± 0.0315, ± 0.0366,
± 0.0382, ± 0.0449, ± 0.0509, ± 0.0643, ± 0.0856, ± 0.1352, ± 0.2062,
± 0.2754, ± 0.3660, ± 0.4355, ± 0.5089, ± 0.5774, ± 0.6590, ± 0.7341, ± 0.8162。
0, ± 0.0006, ± 0.0017, ± 0.0030, ± 0.0025, ± 0.0030, ± 0.0035,
± 0.0045, ± 0.0057, ± 0.0066, ± 0.0085, ± 0.0093, ± 0.0107, ± 0.0115, ± 0.0125,
± 0.0137, ± 0.0141, ± 0.0156, ± 0.0161, ± 0.0179, ± 0.0193, ± 0.0209,
± 0.0227, ± 0.0238, ± 0.0258, ± 0.0268, ± 0.0280, ± 0.0287, ± 0.0292,
± 0.0320, ± 0.0348, ± 0.0394, ± 0.0437, ± 0.0498, ± 0.0615, ± 0.0788,
± 0.1272, ± 0.1988, ± 0.2734, ± 0.3461, ± 0.4257, ± 0.5012, ± 0.5841,
± 0.6502, ± 0.7260, ± 0.8022, ± 0.8818, ± 0.9474; 外倾角为0° 。
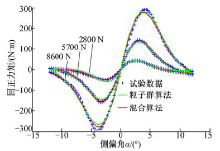
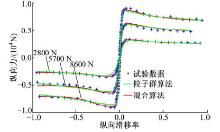
纯侧偏工况的侧向力及回正力矩试验数据:侧偏角
在Matlab/Simulink环境下编程实现粒子群优化算法及修正的G-N算法。先利用粒子群优化算法全局搜索能力辨识UniTire轮胎模型特征参数向量的近似解, 将其作为修正的G-N算法的初始值, 再利用修正的G-N算法局部搜索能力获得其精确解。
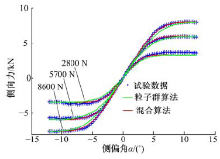
将试验数据的轮胎力/力矩和用辨识结果参数化的UniTire轮胎模型计算得到的轮胎力/力矩绘制成曲线, 如图1~图3所示。
 | 图1 纯纵滑工况纵向力辨识结果Fig.1 Identification results of longitudinal force under pure longitudinal slip condition |
对比图1~图3所示的试验数据和粒子群优化算法的辨识结果, 二者大致吻合, 说明该算法能够获得UniTire轮胎模型特征参数的近似解。对比图1~图3所示的试验数据和混合优化方法的辨识结果, 二者吻合较好, 说明混合优化方法可以得到UniTire轮胎模型特征参数更精确的解。
采用式(26)对辨识结果的残差进行定量分析, 结果如表1所示。
从表1可以看出:粒子群优化算法获得的UniTire轮胎模型特征参数的残差均小于5.5%, 而采用修正的G-N算法进一步辨识得到的特征参数残差均小于3.5%, 可更好地满足构建车辆底盘电控系统硬件在环仿真测试环境的需求。
| 表1 参数辨识结果残差分析 Table 1 Residual analysis of parameters identification results % |
(1)利用粒子群优化算法的全局搜索优势和修正的G-N算法的局部搜索优势对纯纵滑、纯侧偏工况下UniTire轮胎模型的特征参数进行辨识。粒子群优化算法的全局搜索优势有效地解决了修正的G-N算法初始值选择对工程经验依赖的问题, 而修正的G-N算法的局部搜索优势可以弥补粒子群优化算法在局部区域内搜索能力差、收敛速度慢的不足。
(2)对辨识结果进行残差分析, 结果表明:采用混合优化方法获得的UniTire轮胎模型特征参数的残差均小于3.5%, 满足构建车辆底盘电控系统硬件在环仿真测试环境的需求。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|